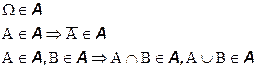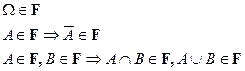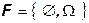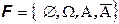что такое сигма алгебра событий
Алгебра и сигма-алгебра



При построении математической модели случайного объекта необходимо не только указать все возможные элементарные исходы опыта, но и определить (перечислить) все возможные события, которые могут произойти в этом опыте. Принято следующее определение:
Алгебра событийAэто набор подмножеств пространства элементарных исходов 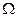
и для любой счетной последовательности
Очевидно, что любая сигма-алгебра является алгеброй, но не наоборот.
Колмогоров показал, что естественной математической моделью для множества событий является сигма-алгебра.
Очевидным примером сигма-алгебры является набор всех подмножеств пространства элементарных исходов – это наибольшая сигма-алгебра, возможная на данном пространстве элементарных исходов.
Наименьшая (тривиальная) сигма-алгебра это следующий набор подмножеств
Алгебры и сигма-алгебры обозначаем жирными наклонными латинскими буквами.
Сигма-алгебра событий
Смотреть что такое «Сигма-алгебра событий» в других словарях:
Булева сигма-алгебра — Борелевская сигма алгебра это минимальная сигма алгебра, содержащая все открытые подмножества топологического пространства (впрочем, она содержит и все замкнутые). Если не оговорено противное, в качестве топологического пространства выступает… … Википедия
Борелевская сигма-алгебра — это минимальная сигма алгебра, содержащая все открытые подмножества топологического пространства (также она содержит и все замкнутые). Эти подмножества также называются Борелевыми. Если не оговорено противное, в качестве топологического… … Википедия
Алгебра (теория множеств) — У этого термина существуют и другие значения, см. Алгебра (значения). Алгебра множеств в теории множеств это непустая система подмножеств, замкнутая относительно операций дополнения (разности) и объединения (суммы). Содержание 1 Определение … Википедия
Алгебра (значения) — Алгебра раздел математики либо математическая структура специального вида (см. Алгебраическая система) Как раздел математики Абстрактная алгебра Алгебра логики раздел математической логики. Коммутативная алгебра Линейная алгебра… … Википедия
Алгебра множеств — У этого термина существуют и другие значения, см. Алгебра (значения). Алгебра множеств в теории множеств это непустая система подмножеств, замкнутая относительно операций дополнения (разности) и объединения (суммы). Содержание 1 Определение … Википедия
Борелевская алгебра — Борелевская сигма алгебра это минимальная сигма алгебра, содержащая все открытые подмножества топологического пространства (впрочем, она содержит и все замкнутые). Если не оговорено противное, в качестве топологического пространства выступает… … Википедия
Пространство элементарных событий — Пространство элементарных событий множество всех различных исходов случайного эксперимента. Элемент этого множества называется элементарным событием или исходом. Пространство элементарных событий называется дискретным, если число его… … Википедия
Случайная величина — это величина, которая принимает в результате опыта одно из множества значений, причём появление того или иного значения этой величины до её измерения нельзя точно предсказать. Формальное математическое определение следующее: пусть вероятностное… … Википедия
Аксиоматика Колмогорова — Аксиоматика Колмогорова общепринятый аксиоматический метод при математическом описании событий и вероятностей; предложен Андреем Николаевичем Колмогоровым[1][2] в 1929, окончательно в 1933; придал теории вероятностей стиль, принятый в… … Википедия
Колмогоровская аксиоматика — Аксиоматика Колмогорова общепринятый аксиоматический подход к математическому описанию события и вероятности; предложен Андреем Николаевичем Колмогоровым[1][2] в 1929, окончательно в 1933; придал теории вероятностей стиль, принятый в современной… … Википедия
Сигма-алгебра
σ-алгебра (си́гма-а́лгебра) — алгебра множеств, замкнутая относительно операции счётного объединения. Сигма-алгебры играют важнейшую роль в теории меры и интегралов Лебега, а также в теории вероятностей.
Содержание
Определение
Семейство 

Замечания
Связанные определения
Примеры
Полезное
Смотреть что такое «Сигма-алгебра» в других словарях:
Булева сигма-алгебра — Борелевская сигма алгебра это минимальная сигма алгебра, содержащая все открытые подмножества топологического пространства (впрочем, она содержит и все замкнутые). Если не оговорено противное, в качестве топологического пространства выступает… … Википедия
Борелевская сигма-алгебра — это минимальная сигма алгебра, содержащая все открытые подмножества топологического пространства (также она содержит и все замкнутые). Эти подмножества также называются Борелевыми. Если не оговорено противное, в качестве топологического… … Википедия
Алгебра (теория множеств) — У этого термина существуют и другие значения, см. Алгебра (значения). Алгебра множеств в теории множеств это непустая система подмножеств, замкнутая относительно операций дополнения (разности) и объединения (суммы). Содержание 1 Определение … Википедия
Алгебра (значения) — Алгебра раздел математики либо математическая структура специального вида (см. Алгебраическая система) Как раздел математики Абстрактная алгебра Алгебра логики раздел математической логики. Коммутативная алгебра Линейная алгебра… … Википедия
Алгебра множеств — У этого термина существуют и другие значения, см. Алгебра (значения). Алгебра множеств в теории множеств это непустая система подмножеств, замкнутая относительно операций дополнения (разности) и объединения (суммы). Содержание 1 Определение … Википедия
Сигма — У этого слова несколько значений: Сигма буква греческого алфавита. Сигма (язык) Стандартное отклонение в теории вероятностей. Сигма алгебра в теории множеств. «Сигма» чешский футбольный клуб. Sigma Corporation японский производитель… … Википедия
Σ-алгебра — (сигма алгебра) это алгебра множеств, замкнутая относительно операции счётного объединения. Сигма алгебры играют важнейшую роль в теории меры и интегралов Лебега, а также в теории вероятностей. Содержание 1 Определение 2 Замечания 3 … Википедия
Борелевская алгебра — Борелевская сигма алгебра это минимальная сигма алгебра, содержащая все открытые подмножества топологического пространства (впрочем, она содержит и все замкнутые). Если не оговорено противное, в качестве топологического пространства выступает… … Википедия
Измеримое пространство — σ алгебра (сигма алгебра) это алгебра множеств, замкнутая относительно операции счётного объединения. Сигма алгебры играют важнейшую роль в теории меры и интегралов Лебега, а также в теории вероятностей. Содержание 1 Определение 2 Замечания 3 … Википедия
Глава 6 Решение задач по теме Сигма-алгебра
Конспект: Алиса Жильцова
дата: 30 сентября 2016 г.
6.1 Задача №1 (№ 2.35 в задачнике)
6.1.1 Условие задачи:
Приведите по два нетривиальных (т.е. \(\Omega\) и \(\emptyset\) не называть) примера такого события A, что:
Упростите выражения: \(\mathcal
6.1.2 Решение:
Приведём по два нетривиальных (т.е. \(\Omega\) и \(\emptyset\) не называть) примера такого события A, что:
Начнём с того, что \(\mathcal
\(\bullet\) A лежит в каждой \(\mathcal
Попробуем привести другой пример события, лежащего во всех \(\mathcal
Событие \(X_ <37>> 0\) означает, что в 37-м подбрасывании выпал орёл. Оно входит во все \(\mathcal
А этот пример еще интереснее! В нем есть ловушка! 🙂
Упростим следующие выражения:
Аналогично предыдущим пунктам получим: \(\mathcal
6.2 Задача №2 Про Агента 007 (№ 2.43 в задачнике)
6.2.1 Условие задачи
Сейчас либо солнечно, либо дождь, либо пасмурно без дождя. Соответственно множество \(\Omega\) состоит из трёх исходов, \(\Omega\) = <солнечно, дождь, пасмурно>. Джеймс Бонд пойман и привязан к стулу с завязанными глазами, но он может на слух отличать, идет ли дождь.
6.2.2 Решение задачи
Введём случайную величину Z, означающую то, что различает Джеймс Бонд. Другими словами, зная Z Джеймс Бонд с легкостью сможет сказать, идёт сейчас дождь или нет. Но он не отличает события <солнечно>и <пасмурно>.
Оформим возможные значения Z в виде таблицы:
| \(\Omega\) | Солнечно | Дождь | Пасмурно |
|---|---|---|---|
| Z | 0 | 1 | 0 |
На бытовом языке такую сигма-алгебру можем описать как список событий, который различает Джеймс Бонд, если бы ему завязали глаза и заткнули бы уши (печально!), т.е. если бы он не знал ничего.
Изобразим такие сигма-алгебры графически:
Ответ: таких сигма-алгебр существует всего 5!
6.3 Задача №3 (2.39 в задачнике)
6.3.1 Условие задачи (перевод)
6.3.2 Решение задачи
Прежде чем приступить к решению следует сразу разобраться в условии задачи. Выделим некоторые ключевые моменты, необходимые для понимания:
\(\bullet\) Первый момент не может являться локальным максимумом. В нашей последовательности \(X_0\) отсутствует, а значит, первый момент не берется в рассмотрение!
\(\bullet\) Для того, чтобы лучше понять, что же такое T, приведем пример с помощью картинки для последовательности (+1,+1,-1,-1,+1,-1):
На графике видим, что вторым локальным максимумом является точка (5,1), а момент T равен 6.
Интуитивно это можно представить так: Джон играет с ребятами, а в момент времени Т его зовёт бабушка Йоко. Что знает Джон? Он знает всё, что было до момента времени Т включительно, а что было после, он уже не видел. Что он может знать? Он знает, чему равно T.
Теперь, детально разобрав условие задачи, ответим на следующие вопросы.
\(\mathcal
Лекция 3 Аксиоматика теории вероятностей
Лекция 3. Аксиоматика теории вероятностей
Вероятность как нормированная мера
О борелевской сигма-алгебре и мере Лебега
Борелевская сигма-алгебра на прямой
3.1. Сигма-алгебра событий
Проверим, что этого набора аксиом достаточно для замкнутости множества относительно других операций над событиями.
Вместо первой аксиомы достаточно предположить, что не пусто, то есть содержит хотя бы один элемент.
Доказательство в обратную сторону выглядит совершенно аналогично.
, где — произвольное подмножество (в предыдущем примере ).
Доказать, что если состоит из элементов, то в множестве всех его подмножеств ровно элементов.
3.2. Вероятность как нормированная мера
Для любого счетного набора попарно непересекающихся множеств (то есть такого, что при всех ) мера их объединения равна сумме их мер:
Иначе говоря, мера есть неотрицательная, счетно-аддитивная функция множеств.
То же самое еще раз и подробно:
Для любого события выполняется неравенство ;
Для любого счетного набора попарно несовместных событий имеет место равенство
Свойства (P1)-(P3) часто называют «аксиомами вероятности».
Для любого конечного набора попарно несовместных событий имеет место равенство
. Доказать методом математической индукции.
По предположению индукции, первое слагаемое в правой части ( 3 ) равно
Вычитаемое в правой части ( 3 ) равно
Подставить ( 4 ),( 5 ) в ( 3 ) и довести до конца шаг индукции.
Приведем пример задачи, в которой использование свойства 9 – самый простой путь решения.
Так как события совместны, придется использовать формулу ( 2 ). Нетрудно убедиться, что
Вычислим количество слагаемых в каждой сумме в формуле ( 2 ). Например, в сумме ровно слагаемых — ровно столько трех-элементных множеств можно образовать из элементов, и каждое такое множество встречается в индексах данной суммы единажды.
Подставляя все вероятности в формулу ( 2 ), получим:
3.3. О борелевской сигма-алгебре и мере Лебега
Борелевская сигма-алгебра на прямой
Мера Лебега
Если вам уже расхотелось читать дальше, сообщаем: мерой Лебега в задачниках и учебниках называют как раз «длину-площадь-объем», так что все в порядке.
Покажем, что это необходимо: построим пример множества на отрезке, мера Лебега которого («длина») просто не существует (множество Витали ).
То есть: если рассмотреть бросание точки наудачу на отрезок, то вычислить вероятность попадания точки в указанное множество в соответствии с геометрической вероятностью нельзя. Значит, это множество нельзя считать событием — мы не умеем вычислить его вероятность!
Таким образом, вся окружность разбивается на классы точек. В каждом классе счетное число точек, и все точки в одном классе получаются друг из друга такими поворотами. Причем эти классы не пересекаются.
Упражнение: какими свойствами «длины» (или меры Лебега) мы воспользовались в этом примере?