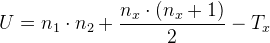критерий манна уитни что такое u
U-критерий Манна — Уитни
U-критерий Манна — Уитни
U-критерий Манна — Уитни (англ. Mann — Whitney U-test ) — статистический критерий, используемый для оценки различий между двумя выборками по уровню какого-либо признака, измеренного количественно. Позволяет выявлять различия в значении параметра между малыми выборками.
Другие названия: критерий Манна — Уитни — Уилкоксона (англ. Mann — Whitney — Wilcoxon, MWW ), критерий суммы рангов Уилкоксона (англ. Wilcoxon rank-sum test ) или критерий Уилкоксона — Манна — Уитни (англ. Wilcoxon — Mann — Whitney test ).
Содержание
История
Данный метод выявления различий между выборками был предложен в 1945 году Френком Уилкоксоном (F. Wilcoxon). В 1947 году он был существенно переработан и расширен Х. Б. Манном (H. B. Mann) и Д. Р. Уитни (D. R. Whitney), по именам которых сегодня обычно и называется.
Описание критерия
Простой непараметрический критерий. Мощность критерия выше, чем у Q-критерия Розенбаума.
Этот метод определяет, достаточно ли мала зона перекрещивающихся значений между двумя рядами (ранжированным рядом значений параметра в первой выборке и таким же во второй выборке). Чем меньше значение критерия, тем вероятнее, что различия между значениями параметра в выборках достоверны.
Ограничения применимости критерия
Использование критерия
Для применения U-критерия Манна — Уитни нужно произвести следующие операции.
U-критерий Манна-Уитни в дипломной, курсовой и магистерской работе по психологии
Подавляющее большинство психологических исследований направлены на достижение двух главных целей:
В данной статье мы рассмотрим основные аспекты использования критерия Манна-Уитни при обработке результатов эмпирического исследования в курсовых и дипломных работах, а также магистерских диссертациях по психологии.
Зачем нужен критерий Манна-Уитни
В психологическом исследовании изучаются не результаты отдельных испытуемых, а обобщенные данные. Например, при изучении особенностей психологических параметров в двух группах изучаются средние значения в этих группах.
Напомним, что среднее (среднее арифметическое) отражает усредненный по группе показатель. Рассчитывается среднее значение следующим образом:
Таким образом, когда мы сравниваем психологические показатели у двух испытуемых, то никакие статистические критерии не нужны. Действительно, пусть в ходе тестирования уровень личностной тревожности Иванова оказался 40 баллов, а Петрова – 50 баллов. В этом случае мы смело говорим, что Петров более тревожен, чем Иванов. Однако, если речь идет о сравнении двух групп, то ситуация усложняется.
Например, мы рассчитали средний уровень личностной тревожности в группе женщин – 58 баллов, и мужчин – 49 баллов. Так как средние значения – это статистические показатели, а не просто числа, то просто так сравнивать их нельзя. То есть, мы не можем сказать, что тревожность женщин выше, чем у мужчин. Но как же быть? Как сравнить показатели тревожности в группах мужчин и женщин?
Для этого и существуют статистические критерии анализа различий. Их расчет позволяет с определённой точностью заключить, существуют различия выраженности показателей в двух группах или нет.
Для анализа различий средних значений в двух группах используется t-критерий Стъюдента. U-критерий Манна-Уитни позволяет сравнивать не средние значения, а выраженность показателей, но в этом случае и средние значения параметров в группах будут различаться соответствующим образом.
Расчет критерия Манна-Уитни: объяснение простыми словами
В подавляющем большинство психологических исследований расчет статистических критериев в том числе и критерия Манна-Уитни производится с помощью статистических программ. Наиболее известные – это SPSS и STATISTICA. Однако несмотря на это важно в общих чертах представлять себе сущность расчета – это придаст студенту-психологу на защите диплома.
Вернёмся к нашему пример с тревожностью мужчин и женщин. Предположим у нас две группы по 10 человек. У каждого испытуемого есть определенное значение личностной тревожности. Нам нужно выяснить, различаются ли уровни тревожности в группах мужчин и женщин. Расчет критерия Манна-Уитни примерно будет проходить по следующим шагам:
Мы привели объяснение на пальцах. Статистические программы для расчета используют специальные алгоритмы, которые позволяют численно оценить эти пересечения данных обеих групп (синих и красных чисел) и сделать вывод о существовании или не существовании различий.
Что нужно знать про критерий Манна-Уитни на защите диплома
U-критерий Манна-Уитни – это непараметрический статистический критерий, использующийся для сравнения выраженности показателей в двух несвязных выборках.
Что такое непараметрический? Не вдаваясь в статистические тонкости, нужно понимать следующее. Параметрические статистические критерии более точные, но они предъявляют более строгие требования к данным. То есть, перед расчетом нужно все данные в группах проверять, например, на нормальность распределение. Это значит, что на графике распределения такие данные должны располагаться в виде колокола – больше всего испытуемых со средними значениями, а меньшинство имеют низкие и высокие показатели. t-критерий Стъюдента является параметрическим критерием.
Непараметрические критерии менее точные, но зато у них нет жестких требований к данным. Эти данные могут быть почти любыми.
Что значит несвязные выборки? Это означает, что группы не пресекаются, то есть в них разные испытуемые. Расчет различий в связных выборках используется, например, при выявлении эффективности тренингов, когда производятся замеры «до» и «после», а потом сравниваются. У критерия Стъюдента есть вариант для связных выборок. Критерий Манна-Уитни используется только для несвязных.
Ограничения критерия Манна-Уитни
«Почему вы выбрали для расчета критерий Манна-Уитни?»
Очень многих студентов-психологов перед защитой диплома пугает именно этот вопрос. Предлагаем в качестве основы для индивидуальных модификаций следующий ответ:
«В данной работе мы не проверяли данные на нормальность распределения, поэтому мы использовали непараметрический статистический критерий анна-Уитни, предназначенный для выявления различий показателей в двух несвязных выборках».
Важно понимать, что фактически этот вопрос означает следующее: «Почему вы выбрали критерий Манна-Уитни, а не критерий Стъюдента». Именно эти критерии наиболее часто используются для сравнительного анализа в психологических исследованиях.
Поэтому в ответе и надо указать, что на нормальность данные не проверяли, например, из-за небольшого объема групп. Поэтому решили остановиться на непараметрическом критерии.
Уровень статистической значимости
Если вы будет пользоваться для расчета критерия Манна-Уитни статистической программой, то в выдаче результатов будут присутствовать два важных показателя:
Пример анализа данных с помощью критерия Манна-Уитни в дипломе по психологии
Результаты сравнительного анализа показателей жизнестойкости у молодежи и людей зрелого возраста
U-критерий Манна-Уитни
U-критерий Манна-Уитни чаще всего используется при обработке результатов эмпирического исследования при написании курсовых, дипломных и магистерских работ по психологии.
U-критерий Манна-Уитни – непараметрический статистический критерий. Это означает, что его требования к группам и измеренным психологическим показателям минимальны:
Как рассчитывается U-критерий Манна-Уитни
Не вдаваясь в математические тонкости, рассмотрим логику расчёта U-критерия Манна-Уитни.
Например, в результате тестирования были получены интегральные показатели осмысленности жизни замужних и незамужних женщин. Одной из задач дипломной работы ставится выявление различий осмысленности жизни у женщин, состоящих и не состоящих в браке. Выборки небольшие (по 30 человек), поэтому можно использовать U-критерий Манна-Уитни.
Процедура расчёта U-критерия Манна-Уитни в самом общем и приближенном виде выглядит следующим образом:
При расчете U-критерия Манна-Уитни с помощью статистических программ выдается значение самого критерия и уровень статистической значимости различий выраженности психологического показателя. Эти показатели необходимо занести в таблицу и выделить те психологические показатели, уровень значимости различий которых в группах ниже, чем 0,05.
Пример расчета U-критерия Манна-Уитни вручную
В результате психодиагностического обследования групп мужчин и женщин (по 20 человек в каждой) были выявлены показатели внутреннего сопротивления при обращении в службу знакомств (в баллах):
Выдвигаем гипотезу о том, что существуют различия внутреннего сопротивления при обращении в службу знакомств между мужчинами и женщинами.
Для проверки гипотезы будет использовать непараметрический критерий U-критерий Манна-Уитни.
Проведем ранжирование показателей в группах мужчин и женщин от меньшего к большему и занесем данные в таблицу.
Библиотека постов MEDSTATISTIC об анализе медицинских данных
Ещё больше полезной информации в нашем блоге в Инстаграм @medstatistic
Критерии и методы
U-КРИТЕРИЙ МАННА-УИТНИ
– непараметрический статистический критерий, используемый для сравнения двух независимых выборок по уровню какого-либо признака, измеренного количественно. Метод основан на определении того, достаточно ли мала зона перекрещивающихся значений между двумя вариационными рядами (ранжированным рядом значений параметра в первой выборке и таким же во второй выборке). Чем меньше значение критерия, тем вероятнее, что различия между значениями параметра в выборках достоверны.
1. История разработки U-критерия
Данный метод выявления различий между выборками был предложен в 1945 году американским химиком и статистиком Фрэнком Уилкоксоном.
В 1947 году он был существенно переработан и расширен математиками Х.Б. Манном (H.B. Mann) и Д.Р. Уитни (D.R. Whitney), по именам которых сегодня обычно и называется.

2. Для чего используется U-критерий Манна-Уитни?
U-критерий Манна-Уитни используется для оценки различий между двумя независимыми выборками по уровню какого-либо количественного признака.
3. В каких случаях можно использовать U-критерий Манна-Уитни?
U-критерий Манна-Уитни является непараметрическим критерием, поэтому, в отличие от t-критерия Стьюдента, не требует наличия нормального распределения сравниваемых совокупностей.
U-критерий подходит для сравнения малых выборок: в каждой из выборок должно быть не менее 3 значений признака. Допускается, чтобы в одной выборке было 2 значения, но во второй тогда должно быть не менее пяти.
Условием для применения U-критерия Манна-Уитни является отсутствие в сравниваемых группах совпадающих значений признака (все числа – разные) или очень малое число таких совпадений.
Аналогом U-критерия Манна-Уитни для сравнения трех и более групп является Критерий Краскела-Уоллиса.
4. Как рассчитать U-критерий Манна-Уитни?
Сначала из обеих сравниваемых выборок составляется единый ранжированный ряд, путем расставления единиц наблюдения по степени возрастания признака и присвоения меньшему значению меньшего ранга. В случае равных значений признака у нескольких единиц каждой из них присваивается среднее арифметическое последовательных значений рангов.
Например, две единицы, занимающие в едином ранжированном ряду 2 и 3 место (ранг), имеют одинаковые значения. Следовательно, каждой из них присваивается ранг равный (3 + 2) / 2 = 2,5.
В составленном едином ранжированном ряду общее количество рангов получится равным:
Наконец, находим значение U-критерия Манна-Уитни по формуле:
5. Как интерпретировать значение U-критерия Манна-Уитни?
Полученное значение U-критерия сравниваем по таблице для избранного уровня статистической значимости (p=0.05 или p=0.01) с критическим значением U при заданной численности сопоставляемых выборок:
Тест Вилкоксона-Манна-Уитни
На практике критерий суммы рангов Вилкоксона или U-критерий используется в качестве альтернативы t-критерию для независимых выборок, если его предпосылки нарушаются. Это имеет место, среди прочего, если проверяемая переменная имеет только порядковый уровень шкалы или если переменные с интервальной шкалой не (приблизительно) нормально распределены в двух популяциях.
Оглавление
Предположения
С этими предположениями тест точен и непротиворечив.
Различные другие точки зрения на критерий Вилкоксона-Манна-Уитни являются частными случаями этой общей формулировки при более сильных предположениях.
Статистика тестов
критерий суммы рангов Вилкоксона и U-критерий Манна-Уитни эквивалентны.
Статистика по Манн-Уитни Ю
Точные критические значения
Существует формула рекурсии, которая позволяет определять критические значения для небольших размеров выборки шаг за шагом и с небольшими затратами времени.
Приблизительные критические значения
можно аппроксимировать нормальным распределением. Тогда критические значения являются результатом критических значений приближенного нормального распределения.
Статистика суммы рангов Wilcoxon
Статистика суммы рангов Уилкоксона равна
Точные критические значения
Формула возникает при условии, что последнее значение в расположении равно × (. X) или Y (. Y).
Приблизительные критические значения
Односторонние гипотезы
Тест также может быть использован для односторонних гипотез.
0>»> ЧАС 0 : а ≤ 0 против. ЧАС 1 : а > 0 <\ displaystyle H_ <0>: a \ leq 0 <\ text 
пример
По данным всеобщего опроса населения в области социальных наук 2006 г. случайным образом было отобрано 20 человек и определен их чистый доход:
| классифицировать | 1 | 2 | 3 | 4-й | 5 | Шестой | 7-е | 8-е | 9 | 10 | 11 | 12-е | 13-е | 14-е | 15-е | 16 | 17-е | 18-е | 19-е | 20-е |
| Чистый доход | 0 | 400 | 500 | 550 | 600 | 650 | 750 | 800 | 900 | 950 | 1000 | 1100 | 1200 | 1500 | 1600 | 1800 | 1900 г. | 2000 г. | 2200 | 3500 |
| Пол | М. | W. | М. | W. | М. | W. | М. | М. | W. | W. | М. | М. | W. | М. | W. | М. | М. | М. | М. | М. |
| Двусторонний тест | Односторонний тест |
|---|---|
Y)=P(X Y)\neq P(X ЧАС 0 : П. ( Икс > Y ) знак равно П. ( Икс Y ) против. ЧАС 1 : П. ( Икс > Y ) ≠ П. ( Икс Y ) <\ Displaystyle H_ <0>: P (X> Y) = P (X Y) \ neq P (X  Y) = P (X Y) \ neq P (X Y) = P (X Y) \ neq P (X | Y)=P(X Y)>P(X ЧАС 0 : П. ( Икс > Y ) знак равно П. ( Икс Y ) против. ЧАС 1 : П. ( Икс > Y ) > П. ( Икс Y ) <\ Displaystyle H_ <0>: P (X> Y) = P (X Y)> P (X  Y) = P (X Y)> P (X Y) = P (X Y)> P (X |
Мы также должны предположить, что если применима нулевая гипотеза, распределение доходов будет полностью таким же.
Для нашего примера мы получаем (индекс M = мужчины, W = женщины)
Двусторонний тест
Точные критические значения
Приблизительные критические значения
Односторонний тест
Точные критические значения
Приблизительные критические значения
Таблица критических значений U-статистики Манна-Уитни
выполнение
Тест Манна-Уитни-Уилкоксона (гипотеза равных распределений по сравнению с подходящими альтернативами) плохо документирован во многих программных пакетах. Некоторые пакеты неправильно обрабатывают привязки или не могут документировать асимптотические методы (например, исправление для непрерывности). Во время обзора в 2000 году обсуждались некоторые из следующих пакетов: