что такое вычет функции комплексной переменной
Что такое вычет функции комплексной переменной
Обозначается вычет
Вычет функции в конечной изолированной особой точке равен коэффициенту С-1 при первой отрицательной степени в разложении функции в ряд Лорана в окрестности этой точки, т.е. при 1/(z—z0) для z0, принадлежащей области комплексных чисел:
ПРИМЕР 1. Вычисление вычета функции в ее конечных особых точках.
Если конечная особая точка z0 является устранимой особой точкой функции f(z), то
ПРИМЕР 2. Вычисление вычета в устранимой особой точке.
ПРИМЕР 3. Вычисление вычета в полюсе порядка n.
ПРИМЕР 4. Вычисление вычета в простом полюсе.
ПРИМЕР 5. Вычисление вычета в существенной особой точке.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Что такое вычеты в ТФКП
ТФКП Вычеты, интегралы
Здравствуйте! Помогите, пожалуйста, вычислить с помощью вычетов интеграл

Снова всем доброго времени суток! Не знает ли кто-нибудь из посещающих данный форум, как заставить.
Что такое файловый буфер? Что такое режим (модификатор) доступа, при работе с файлами?
Что такое файловый буфер? Что такое режим (модификатор) доступа, при работе с файлами?
Что такое IIS и что такое PWS? Почему одно без другого не работает?
вот уже второй день пытаюсь немного разобраться в АСП. накидал небольшую тестовую страничку. но с.
Действительно, «вычет» по-английски «residue», то есть «остаток».
Первое, говоря грубым простым языком, указывает на масштаб поведения функции как полюса первого порядка. Если функция ограничена в области, вычет в каждой точке нулевой. Если функция A/(z-a), то в z=a вычет равен A, а во всех остальных точках нулю. Во всех остальных случаях смотрим, насколько функция в окрестности рассматриваемой точки похожа на полюс первого порядка и масштабный коэффициент A принимаем за значение вычета.
В ТФКИ голоморфная ф-ция имеет спец. свойства. В частности, значение ф-ции в точке можно восстановить по поведению ф-ции в окрестности. Интеграл ф-ции по замкнутому контуру равен (с точностью до ) сумме вычетов внутри контура.
Грубая аналогия: поток электрического поля через замкнутую поверхность (сферу, поверхностью куба и т.п.) определяется суммой всех зарядов внутри этого ограниченного объёма (шара, куба и т.п.). Если мы будем поверхность стягивать в точку, поток в конечном счёте будет стремиться к величине, пропорциональной точечному заряду, размещённому в этой точке.
Вычеты аналитических функций
Раздел: 13. Теория функций комплексной переменной
4. Вычеты аналитических
1. Вычеты аналитических функций. Основная теорема о вычетах
2. Бесконечно удаленная точка
1. Вычеты аналитических функций. Основная теорема о вычетах
Вычетом функции f ( z )
в изолированной точке
(обозначение res f ( a ) 1 ) называется число
Из формулы для определения коэффициентов ряда Лорана
функции f ( z ) при n = −1 непосредственно вытекает, что
Отсюда следует, что в устранимой особой точке вычет все-
Нахождение вычета в полюсе порядка n
Для ее вывода достаточно умножить лорановское разложение
в выражение производной невозможно, ибо
Для полюсов первого порядка формула (3) принимает осо-
Если при этом в окрестности точки a функция f ( z ) опре-
делена как частное двух аналитических в окрестности этой точке функций:
причем ϕ ( a ) ≠ 0, а ψ ( z ) имеет в a нуль первого порядка (т.е.
ψ ( a ) = 0, ψ ′( a ) ≠ 0 ), то формулу (4) можно заменить следующей:
Применение теории вычетов основывается главным обра-
зом на следующей важной теореме.
Теорема 1. (О.Коши, 1825 г.) Пусть функция
∫ f ( z ) dz = 2 π i ∑ res f ( a k ).
Принципиальная важность теоремы о вычетах заключается в том, что она позволяет свести вычисление величины «в целом», какой является интеграл по замкнутому контуру конечной величины, к вычислению величин «в малом», дифференциальных величин, какими являются вычеты. Действительно, вычеты вычисляются с помощью интегралов по бесконечно малым кон-
турам или даже с помощью предельного перехода (формулы (3), (4) и (5)). Метод сведения величин «в целом» к вычислению дифференциальных величин является обычным в математическом анализе (сравни вычислению интегралов с помощью первообразных, которые определяются на основании извесных производных).
2. Бесконечно удаленная точка
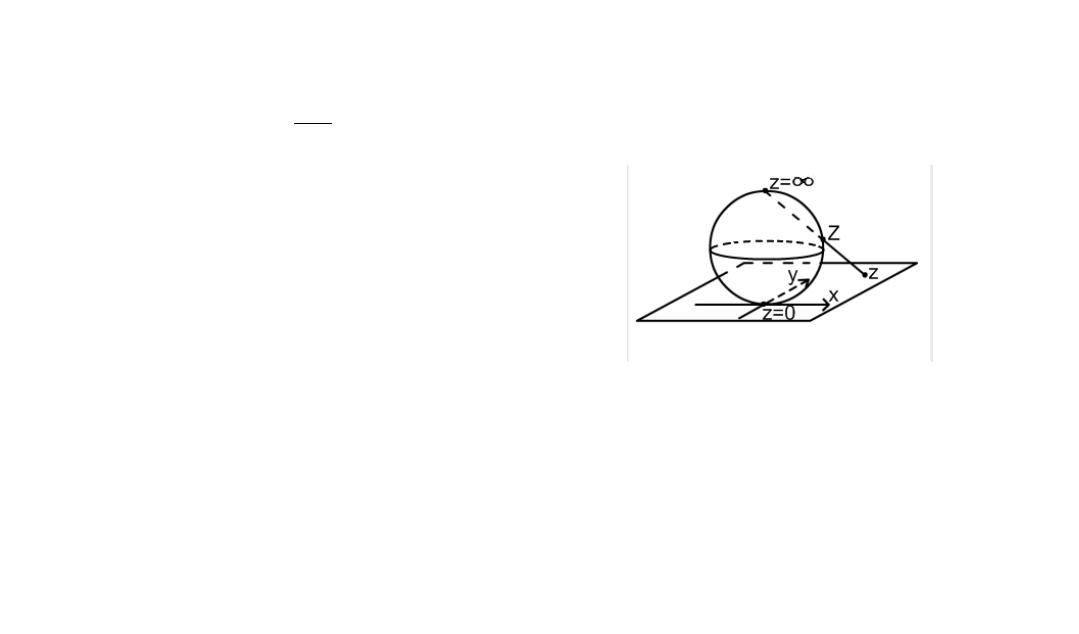
До сих пор мы рассматривали лишь конечные точки плоскости комплексной переменной, однако для изучения некоторых вопросов полезно ввести и бесконечно удаленную точку. Это нагляднее всего сделать с помощью, так называемой,
стереографической проекции плоскости z на сферу, касающуюся плоскости своим южным полюсом.
ным полюсом. Точки Z считают сферическими изображениями комплексных чисел z и саму сферу называют числовой.
Чтобы распространить соответствие на всю сферу, на плоскости вводят условную бесконечно удаленную точку
(комплексное число z = ∞ ) и считают ее соответствующей северному полюсу сферы. Число z = ∞ не участвует в арифметических операциях, как обычные комплексные числа. Однако го-
ворят, например, что последовательность < z k >сходится к бес-
разуют последовательность, сходящуюся к северному полюсу сферы.
Плоскость комплексной переменной с присоединенной к ней бесконечно удаленной точкой называют полной комплексной плоскостью (плоскость без такой точки называют
открытой). Как мы видели, полная комплексная плоскость эквивалентна сфере, и для геометрических представлений понятий, связанных с бесконечно удаленной точкой, очень удобно прибегать к сферическому изображению комплексных чисел.
ки). После введения этого понятия можно рассматривать области, содержащие бесконечно удаленную точку внутри или на границе, т.е. неограниченные области.
Определение порядка связности, данное ранее для ограниченных областей, без всяких изменений переносится на неограниченные области (например, окрестность точки z = ∞ с включением последней оказывается односвязной областью, а та же окрестность с исключением z = ∞ – двусвязной).
Пусть функция f ( z ) аналитична в некоторой окрестности
бесконечно удаленной точки (кроме самой точки z = ∞ ; понятие аналитичности в этой точке пока еще не определено). На такую функцию без всяких изменений распространяется определение особых точек: говорят, что z = ∞ является устранимой особой точкой, полюсом или существенно особой точкой функции f ( z ) в зависимости от того, конечен, беско-
Однако критерии типа особой точки, связанные с разложением Лорана, изменятся, что видно из следующего рассужде-
Вычеты аналитических функций
Раздел: 13. Теория функций комплексной переменной
4. Вычеты аналитических
1. Вычеты аналитических функций. Основная теорема о вычетах
2. Бесконечно удаленная точка
1. Вычеты аналитических функций. Основная теорема о вычетах
Вычетом функции f ( z )
в изолированной точке
(обозначение res f ( a ) 1 ) называется число
Из формулы для определения коэффициентов ряда Лорана
функции f ( z ) при n = −1 непосредственно вытекает, что
Отсюда следует, что в устранимой особой точке вычет все-
Нахождение вычета в полюсе порядка n
Для ее вывода достаточно умножить лорановское разложение
в выражение производной невозможно, ибо
Для полюсов первого порядка формула (3) принимает осо-
Если при этом в окрестности точки a функция f ( z ) опре-
делена как частное двух аналитических в окрестности этой точке функций:
причем ϕ ( a ) ≠ 0, а ψ ( z ) имеет в a нуль первого порядка (т.е.
ψ ( a ) = 0, ψ ′( a ) ≠ 0 ), то формулу (4) можно заменить следующей:
Применение теории вычетов основывается главным обра-
зом на следующей важной теореме.
Теорема 1. (О.Коши, 1825 г.) Пусть функция
∫ f ( z ) dz = 2 π i ∑ res f ( a k ).
Принципиальная важность теоремы о вычетах заключается в том, что она позволяет свести вычисление величины «в целом», какой является интеграл по замкнутому контуру конечной величины, к вычислению величин «в малом», дифференциальных величин, какими являются вычеты. Действительно, вычеты вычисляются с помощью интегралов по бесконечно малым кон-
турам или даже с помощью предельного перехода (формулы (3), (4) и (5)). Метод сведения величин «в целом» к вычислению дифференциальных величин является обычным в математическом анализе (сравни вычислению интегралов с помощью первообразных, которые определяются на основании извесных производных).
2. Бесконечно удаленная точка
До сих пор мы рассматривали лишь конечные точки плоскости комплексной переменной, однако для изучения некоторых вопросов полезно ввести и бесконечно удаленную точку. Это нагляднее всего сделать с помощью, так называемой,
стереографической проекции плоскости z на сферу, касающуюся плоскости своим южным полюсом.
ным полюсом. Точки Z считают сферическими изображениями комплексных чисел z и саму сферу называют числовой.
Чтобы распространить соответствие на всю сферу, на плоскости вводят условную бесконечно удаленную точку
(комплексное число z = ∞ ) и считают ее соответствующей северному полюсу сферы. Число z = ∞ не участвует в арифметических операциях, как обычные комплексные числа. Однако го-
ворят, например, что последовательность < z k >сходится к бес-
разуют последовательность, сходящуюся к северному полюсу сферы.
Плоскость комплексной переменной с присоединенной к ней бесконечно удаленной точкой называют полной комплексной плоскостью (плоскость без такой точки называют
открытой). Как мы видели, полная комплексная плоскость эквивалентна сфере, и для геометрических представлений понятий, связанных с бесконечно удаленной точкой, очень удобно прибегать к сферическому изображению комплексных чисел.
ки). После введения этого понятия можно рассматривать области, содержащие бесконечно удаленную точку внутри или на границе, т.е. неограниченные области.
Определение порядка связности, данное ранее для ограниченных областей, без всяких изменений переносится на неограниченные области (например, окрестность точки z = ∞ с включением последней оказывается односвязной областью, а та же окрестность с исключением z = ∞ – двусвязной).
Пусть функция f ( z ) аналитична в некоторой окрестности
бесконечно удаленной точки (кроме самой точки z = ∞ ; понятие аналитичности в этой точке пока еще не определено). На такую функцию без всяких изменений распространяется определение особых точек: говорят, что z = ∞ является устранимой особой точкой, полюсом или существенно особой точкой функции f ( z ) в зависимости от того, конечен, беско-
Однако критерии типа особой точки, связанные с разложением Лорана, изменятся, что видно из следующего рассужде-