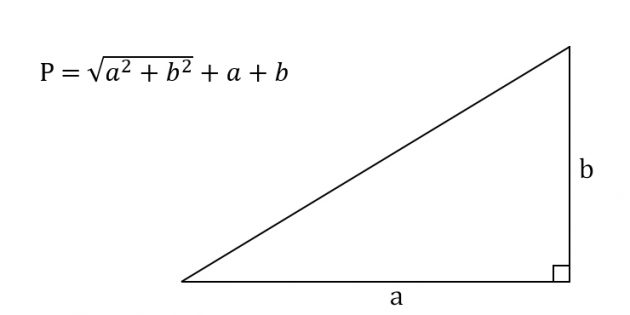что такое периметр треугольника определение

Как найти периметр треугольника

Учимся находить периметр треугольника разными способами, а также тренируем полученные знания на примерах задач.

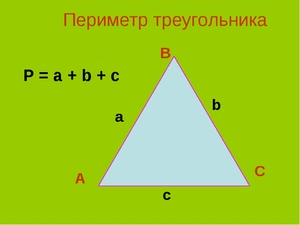
Периметр треугольника

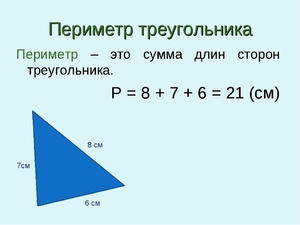
Периметр треугольника — это сумма длин всех его сторон.

Треугольник — это геометрическая фигура, которая состоит из трех точек (вершин), не лежащих на одной прямой. Эти точки попарно соединены тремя отрезками, которые называются сторонами (ребрами) многоугольника.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Рассмотрим несколько способов нахождения периметра рассматриваемой фигуры. Каждая из предложенных формул опирается на те величины, которые нам уже известны.

Способы нахождения

По трем сторонам

Если мы уже знаем длину каждого ребра фигуры, расчет периметра будет проходить так:

где a, b и с — это стороны треугольника.

В случае, если нам известны стороны равнобедренного треугольника (у которого два ребра равны), формула для расчета периметра выглядит следующим образом:

где a — основание фигуры, а b и с — равные ребра.

Треугольник может также быть равносторонним (когда все стороны равны). Тогда P будем находить в соответствии с расчетами:

где a — это любая сторона фигуры.

По площади и радиусу вписанной окружности

Когда нам известна площадь данного многоугольника и радиус вписанной в него окружности, расчет P выглядит так:

где S — площадь фигуры, r — радиус вписанной в нее окружности.

По двум сторонам и углу между ними

Так как нам известен угол и две стороны, которыми он образован, мы можем найти третью сторону треугольника по теореме косинусов. И потом уже вычислить сумму длин всех ребер фигуры.

Теорема косинусов выглядит так:

где α — известный угол.

Тогда формула для расчета периметра всей фигуры в этом случае:

По боковой стороне и высоте (для равнобедренного)

Возвращаясь к свойствам равнобедренного треугольника, вспоминаем, что высота, проведенная к основанию треугольника из противоположной вершины, является одновременно высотой, биссектрисой и медианой. Это значит, что оба прямоугольных треугольника, которые она образует, равны между собой.

Формула для поиска периметра нашего равнобедренного будет опираться на теорему Пифагора. Пусть 1/2 основания (с) = d. Тогда:

где a — сторона равнобедренного треугольника и гипотенуза прямоугольного, h — высота равнобедренного и катет прямоугольного.

Не забываем, что d — это лишь половина основания равнобедренного треугольника, поэтому для поиска периметра результат нужно будет умножить на 2.

По двум катетам (для прямоугольного)

Еще раз вспомним теорему Пифагора для нахождения гипотенузы (обозначим ее буквой с).

где a и b — катеты треугольника.

Подставляем значение c в формулу для нахождения периметра и получаем:

Примеры решения задач

Для тренировки полученных знаний, рассмотрим несколько примеров решения задач на поиск периметра треугольника.

Задача №1

Какой P треугольника, если его стороны равны 6 см, 7 см и 3 см.

Решение:

Подставляем в формулу P = a+b+c известные величины и получаем: P = 6+7+3=16 см.

Задача №2

Известно, что основание равнобедренного треугольника равно 6 см, а его боковая сторона — 4 см. Найти P фигуры.

Решение:

Для данного случая подходит формула P=a+2b, подствляем значения: \(P=6+4\times2 = 14\) см.

Задача №3

Решение:

Задача №4

Дан равнобедренный треугольник. Нам известна его боковая сторона (4 см) и высота, опущенная к основанию (2 см). Нужно вычислить периметр фигуры.

Решение:

Задача №5

Дан прямоугольный треугольник с катетами 5 см и 7 см. Определить периметр фигуры.

Решение:

В формулу \(P=\sqrt+a+b\) подставляем известные значения: \(P=\sqrt<5^2+7^2>+5+7 = \sqrt<74>+12\) см.

Источник

Периметры фигур. Периметр треугольника.

имеет ту же размерность величин, что и длина.

буквами, соответствующими обозначению противоположных вершин.

Периметр треугольника равен сумме длин его сторон, общая формула:

Формула периметра треугольника для треугольника АВС:

Периметр равностороннего треугольника.

Чтобы найти периметр равностороннего треугольника (или найти периметр правильного

треугольника), нужно знать его сторону.

В общем случае для нахождения периметра треугольника используют формулу:

Поскольку в равностороннем треугольнике все три стороны равны, формула упрощается:

Таким образом, периметр равностороннего треугольника находится по такой формуле:

где а — длина его стороны.

Периметр равнобедренного треугольника.

Чтобы найти периметр равнобедренного треугольника, нужно знать всего две его стороны — основание

Поскольку у равнобедренного треугольника две стороны равны (боковые), найти периметр

равнобедренного треугольника можно по такой формуле:

То есть, периметр равнобедренного треугольника равен сумме длин основания и

Источник

Нахождение периметра треугольника: формула и задачи

В данной публикации мы рассмотрим, каким образом можно посчитать периметр треугольника и разберем примеры решения задач.

Формула вычисления периметра

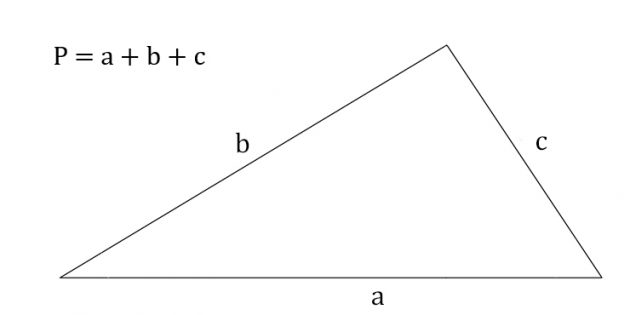
Периметр (P) любого треугольника равняется сумме длин всех его сторон.

P = a + b + c

Периметр равнобедренного треугольника

Равнобедренным называют треугольник, у которого две боковые стороны равны (примем их за b). Сторона a, имеющая отличную от боковых длину, является основанием. Таким образом, периметр можно считать так:

P = a + 2b

Периметр равностороннего треугольника

Равносторонним или правильным называется треугольник, у которого все стороны равны (примем ее за a). Периметр такой фигуры вычисляется так:

P = 3a

Примеры задач

Задание 1
Найдите периметр треугольника, если его стороны равны: 3, 4 и 5 см.

Решение:
Подставляем в формулу известные по условиям задачи величины и получаем:
P = 3 см + 4 см + 5 см = 12 см.

Задание 2
Найдите периметр равнобедренного треугольника, если его основание равняется 10 см, а боковая сторона- 8 см.

Решение:
Как мы знаем, боковые стороны равнобедренного треугольника равны, следовательно:
P = 10 см + 2 ⋅ 8 см = 26 см.

Источник

Формулы определения периметра, площади и сторон треугольника

Треугольник — это элементарная геометрическая фигура, содержащая минимально возможное количество составляющих — три.

Точки соприкосновения сторон являются вершинами его углов, обозначаются заглавными латинскими символами A; B и C. Отрезки между вершинами являются сторонами или гранями треугольника и обозначаются названиями этих вершин: AB; BC; CA или прописной буквой противолежащего угла (вершины): AB=c; BC=a; CA=b.

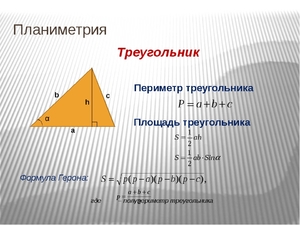
Периметр равен длине всех сторон фигуры, у треугольника он равен сумме трех сторон:

Высота треугольника — это перпендикуляр от прямой, на которой лежит основание, до одноименной вершины, обозначается h.

Площадь составляет величину поверхности, заключенной внутри фигуры, обозначается S. Произведение основания на высоту дает значение площади. Ее можно определить и по формуле Герона:

Из этого видео вы узнаете, как найти площадь треугольника.

Классификация треугольников

Треугольник состоит из сторон и углов, сумма его углов всегда равна 180 градусов: A+B+C=180°.

Описание

Чтобы описать любой треугольник, достаточно указать:

Данных из любого пункта достаточно для построения заданной фигуры и вычисления всех ее параметров, используя теорему косинусов:

Подставляя известные значения, получим уравнение, решив которое узнаем неизвестные величины.

Cos90°=0, поэтому для прямоугольного треугольника c*c=a*a+b*b, где a и b — катеты, c — гипотенуза, сторона, лежащая напротив прямого угла.

Примеры

Если известно три параметра любого треугольника — два угла и сторона или две стороны и угол между ними, то ничего особенно сложного в нахождении неизвестных параметров треугольника — периметра, площади или высоты — нет. Нужно только внимательно производить простые вычисления. Иногда можно проявить и смекалку, разбив фигуру на несколько более простых в вычислении, например, прямоугольных треугольников. В каждом конкретном случае все зависит от исходных данных. Все формулы и вычисления, приведенные выше, верны для плоских фигур; для расположенных на сферической поверхности ход вычислений будет иным.

Видео

Это видео поможет вам закрепить полученные знания.

Источник

Геометрия. 7 класс

Конспект урока

Перечень рассматриваемых вопросов:

Треугольник – геометрическая фигура, образованная тремя точками, не лежащими на одной прямой, которые соединены между собой отрезками.

Периметр треугольника – это сумма длин всех его сторон.

Стороны треугольника– отрезки, соединяющие вершины треугольника.

Равные треугольники –треугольники, которые можно совместить наложением.

1. Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.

Теоретический материал для самостоятельного изучения.

Вы уже познакомились с основными геометрическими фигурами:

Рассмотрим геометрическую фигуру, которая также является одной из основополагающих– треугольник.

Треугольник – геометрическая фигура, образованная тремя точками, не лежащими на одной прямой, которые соединены между собой отрезками.

Точки, с которых начиналось построение, называются вершинами треугольника.

Отрезки, соединяющие вершины треугольника, называются сторонами треугольника.

А, В, С – вершины треугольника АВС.

АВ, ВС, СА – стороны треугольника АВС.

∠А,∠В,∠С – углы треугольника АВС.

Периметр треугольника – это сумма длин всех его сторон.

Рассмотрим виды треугольников.

Их можно разделить по виду и соотношению углов, а также по соотношению сторон.

По углам треугольник может быть:

– остроугольным, если все его углы являются острыми, (т.е. меньше 90°).

– тупоугольным, если один из его углов тупой(т.е. больше 90°).

– прямоугольным, если один угол 90° (т.е. прямой).

По сторонам треугольник бывает:

– разносторонний, если все его стороны имеют различную длину;

– равнобедренный, если две его стороны равны между собой;

– равносторонний,если у него все три стороны равны между собой.

Напомним, что две фигуры, в том числе и треугольник, можно сравнить. ∆ АВС = ∆ А₁В₁С₁

Два треугольника называются равными, если их можно совместить наложением. При этом попарно совмещаются вершины, углы и стороны треугольников.

Следует помнить, что если два треугольника равны, то элементы (стороны и углы) одного треугольника соответственно равны элементам (сторонам и углам) другого треугольника.

Свойство равных треугольников.

В равных треугольниках против соответственно равных сторон лежат равные углы. Обратное утверждение тоже верно: против соответственно равных углов лежат равные стороны.

Равенство треугольников также можно установить, не производя наложения фигур друг на друга, а сравнивая лишь некоторые элементы этих фигур. Это станет возможным при изучении признаков равенства треугольников.

Внешний угол треугольника.

Введём определение внешнего угла треугольника.

Внешним углом треугольника при данной вершине называется угол, смежный с углом треугольника при этой вершине.

У каждого угла треугольника есть два угла, смежных с ним, т.е. у треугольника шесть внешних углов.

Отметим, что при одной вершине внешние углы равны, как вертикальные.

Разбор решения заданий тренировочного модуля.

Найдите градусную меру внешнего ∠В, треугольника АВС, если ∠АВС = 60°.

По рисунку видно, что угол В внешний угол треугольника и он является смежным к углу АВС, следовательно, их сумма равна 180°.

∠В = 180° – ∠АВС = 180° – 60° = 120°

Периметр ∆АВС равен 58 см, сторона АВ = 20 см, сторона ВС >АС на 5 см. Найдите стороны ВС и АС.

Решение: Для решения задачи воспользуемся формулой периметра треугольника Р_∆АВС = АВ + ВС + АС. Обозначим сторону АС за х, тогда сторона ВС равна х + 5, составим уравнение.

5. х = 16,5 см – сторона АС.

6. 16,5 + 5 = 21,5 см – сторона ВС.

Источник