что такое общая касательная
Общие касательные
Выясним сколько общих касательных имеют две окружности и как эти общие касательные могут быть расположены.
Если две окружности не пересекаются и окружность меньшего радиуса лежит внутри окружности большего радиуса, то они не имеют общих касательных.
В другом случае не пересекающиеся окружности имеют четыре общие касательные.
внешние общие касательные
При этом, если обе окружности лежат по одну сторону от касательной (в одной полуплоскости), то такая касательная называется внешней.
внутренние общие касательные
Если окружности лежат по разные стороны от общей касательной (в разных полуплоскостях), то такая касательная называется внутренней.
Если две окружности имеют внутреннее касание, то у них есть одна общая касательная.
При внешнем касании две окружности имеют три общие касательные.
Две пересекающиеся окружности имеют две общие касательные.
Окружность. Касательная к окружности.
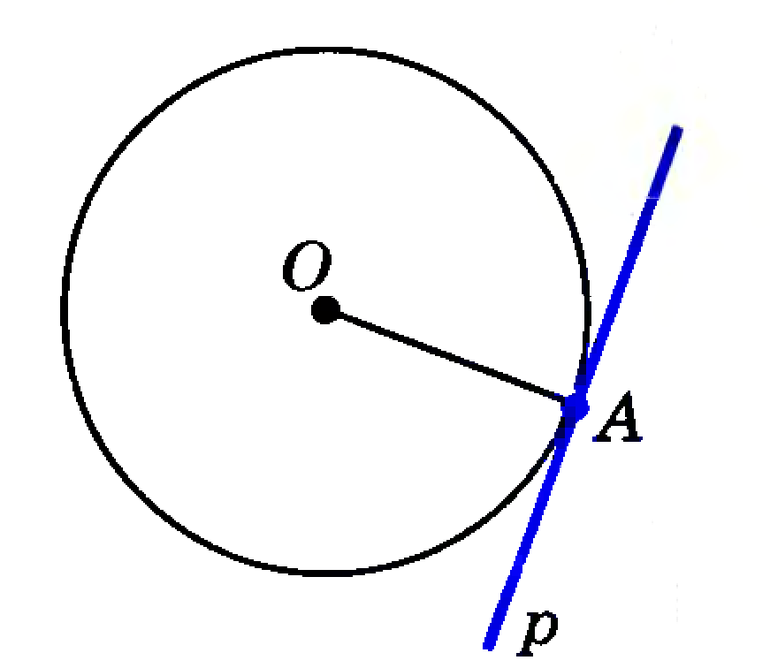
Прямая (MN), имеющая с окружностью только одну общую точку (A), называется касательной к окружности.
Общая точка называется в этом случае точкой касания.
Возможность существования касательной, и притом проведенной через любую точку окружности, как точку касания, доказывается следующей теоремой.
Теорема.
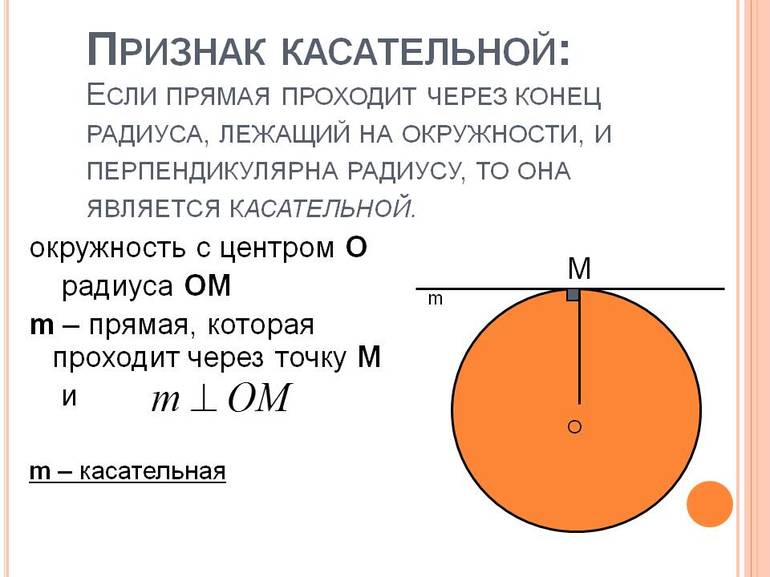
Если прямая перпендикулярна к радиусу в его конце, лежащем на окружности, то эта прямая — касательная.
Допустим противное: пусть MN имеет с окружностью еще другую общую точку, например B. Тогда прямая OB была бы радиусом и, следовательно, равнялась бы OA.
Обратная теорема.
Если прямая касательная к окружности, то радиус, проведенный в точку касания, перпендикулярен к ней.
Следствие.
Через всякую данную на окружности точку можно провести касательную к этой окружности и притом только одну, так как через эту точку можно провести перпендикуляр, и притом только один, к радиусу, проведенному в нее.
Теорема.
Касательная параллельная хорде, делит в точке касания дугу, стягиваемую хордой, пополам.
Пусть прямая AB касается окружности в точке M и параллельна хорде СD. Требуется доказать, что ∪CM= ∪MD.
Проведя через точку касания диаметр ME, получаем: EM ⊥ AB и следовательно, EM ⊥ СD. Поэтому СM=MD.
Через данную точку провести касательную к данной окружности.
Если данная точка находится на окружности, то проводят через нее радиус и через конец радиуса перпендикулярную прямую. Эта прямая будет искомой касательной.
Рассмотрим тот случай, когда точка дана вне круга.
Пусть требуется провести к окружности с центром O касательную через точку A. Для этого из точки A, как из центра, описываем дугу радиусом AO, а из точки O, как центра, пересекаем эту дугу в точках B и С раствором циркуля, равным диаметру данного круга.
Следствие.
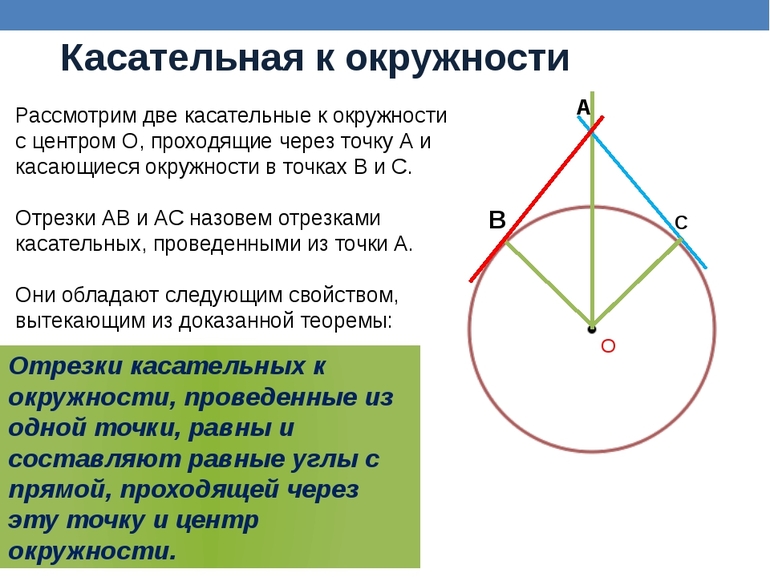
Две касательные, проведенные из одной точки к окружности, равны и образуют равные углы с прямой, соединяющей эту точку с центром.
Так AD=AE и ∠OAD = ∠OAE потому, что прямоугольные треугольники AOD и AOE, имеющие общую гипотенузу AO и равные катеты OD и OE (как радиусы), равны. Заметим, что здесь под словом “касательная” подразумевается собственно “отрезок касательной” от данной точки до точки касания.
Касательные к окружности
В обычной жизни ты очень хорошо представляешь себе, что значит слово «коснуться».
И вот представь себе, в математике тоже существует такое понятие.
В этой теме мы разберёмся с выражениями «прямая касается окружности» и «две окружности касаются».
Касательные к окружности. Коротко о главном
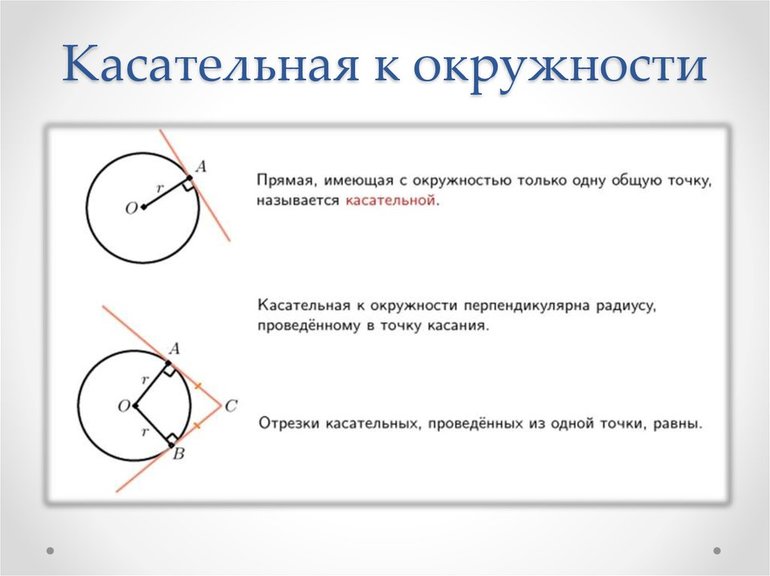
Касательная – прямая, которая имеет с окружностью только одну общую точку.
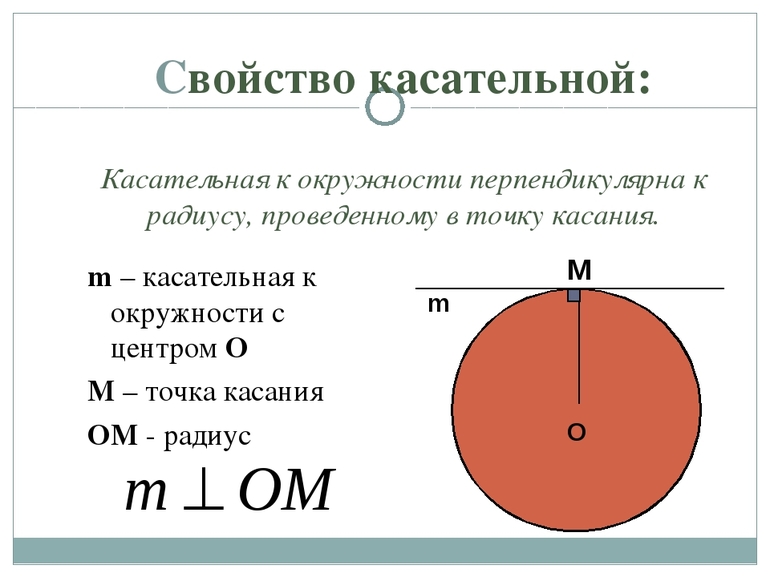
Касательная окружности перпендикулярна радиусу, проведённому в точку касания.
Угол между касательной и хордой равен половине градусной меры дуги, которая находится внутри угла: \( \displaystyle \angle CAB=\frac<1><2>\angle AOB\), где:
Касание окружностей: если две окружности касаются, то точка касания лежит на прямой, соединяющей их центры. Кроме того, эта прямая перпендикулярна касательной, проведённой в точку касания окружностей:
Внешнее касание
Внутреннее касание
Для двух окружностей с центрами \( \displaystyle <
Касательные к окружности. Определения и основная теорема
Прямая касается окружности, если имеет с ней ровно одну общую точку.
Такая прямая называется касательной к данной окружности.
Посмотри-ка внимательно: очень похоже на жизнь, не правда ли? Прямая на картинке лишь чуть-чуть дотрагивается до окружности, касается ее.
Ну вот, и точно так же:
Две окружности касаются, если имеют ровно одну общую точку.
Что же тебе нужно знать о касательных и касающихся окружности?
Самая важная теорема гласит, что:
Радиус, проведённый в точку касания, перпендикулярен касательной.
Запомни это прямо как таблицу умножения! Все остальные факты о касательных и касающихся окружностях основаны именно на этой теореме.
Доказывать её мы здесь не будем, а вот как эта самая важная теорема работает, увидим сейчас несколько раз.
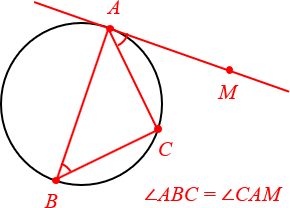
Угол между касательной и хордой
Угол между касательной и хордой равен половине градусной меры дуги, которая находится внутри угла.
Прежде всего: как это понимать? Подробнее о том, что такое «градусная мера дуги», написано в теме «Окружность. Вписанный угол».
Здесь напомним только, что в дуге столько же градусов, сколько в центральном угле, заключающем эту дугу.
То есть «градусная мера дуги» – это «сколько градусов в центральном угле» – и всё!
Ну вот, как говорит Карлсон, продолжаем разговор. Рисуем ещё раз теорему об угле между касательной и хордой.
Смотри, хорда \( \displaystyle AB\) разбила окружность на две дуги. Одна дуга находится ВНУТРИ угла \( \displaystyle BAC\), а другая дуга – внутри угла \( \displaystyle BAD\).
И теорема об угле между касательной и хордой говорит, что \( \displaystyle \angle CAB\) равен ПОЛОВИНЕ угла \( \displaystyle AOB\), \( \displaystyle \angle DAB\) равен ПОЛОВИНЕ большего (на рисунке — зеленого) угла \( \displaystyle AOB\).
При чем же тут тот факт, что радиус, проведенный в точку касания, перпендикулярен касательной?
Сейчас и увидим. \( \displaystyle OA\) – радиус, \( \displaystyle AC\) – касательная.
Значит, \( \displaystyle \angle OAC=90<>^\circ \).
И осталось вспомнить, что сумма углов треугольника \( \displaystyle AOB\) равна \( \displaystyle 180<>^\circ \).
Здорово, правда? И самым главным оказалось то, что \( \displaystyle \angle OAC=90<>^\circ \).
Равенство отрезков касательных
Задумывался ли ты над вопросом «а сколько касательных можно провести из одной точки к одной окружности»? Вот, представь себе, ровно две! Вот так:
А ещё более удивительный факт состоит в том, что:
Отрезки касательных, проведённых из одной точки к одной окружности, равны.
То есть, на нашем рисунке, \( \displaystyle AB=AC\).
И для этого факта тоже самым главным является то, что радиус, проведённый в точку касания, перпендикулярен касательной.
Проведём радиусы \( \displaystyle OB\) и \( \displaystyle OC\) и соединим \( \displaystyle O\) и \( \displaystyle A\).
\( \displaystyle OB\) – радиус.
\( \displaystyle AB\) – касательная, значит, \( \displaystyle OB\bot AB\).
Ну, и так же \( \displaystyle OC\bot AC\).
Получилось два прямоугольных треугольника \( \displaystyle AOB\) и \( \displaystyle AOC\), у которых:
(заглядываем в тему «Прямоугольный треугольник«, если не помним, когда бывают равны прямоугольные треугольники).
Но раз \( \displaystyle \Delta AOB=\Delta AOC,\) то\( \displaystyle AB=AC\). УРА!
И ещё раз повторим – этот факт тоже очень важный:
Отрезки касательных, проведённых из одной точки, – равны.
И есть ещё один факт, который мы здесь не будем доказывать, но он может оказаться тебе полезен при решении задач.
Для любой прямой \( \displaystyle AD\), пересекающей окружность,\( \displaystyle AD\cdot AC=A<^<2>>\), где \( \displaystyle AB\) – отрезок касательной.
Хитроумными словами об этом говорят так:
«Квадрат длины отрезка касательной равен произведению секущей на её внешнюю часть».
Страшно? Не бойся, помни только, что в буквах это:
Общая касательная к двум окружностям
Прямая, которая касается двух окружностей, называется их общей касательной.
Общие касательные бывают внешние и внутренние. Смотри на картинки.
Две внутренние общие касательные:
Две внешние общие касательные:
А всего – четыре! Не больше, но может быть меньше.
Есть только две внешние общие касательные.
Или так: одна внутренняя и две внешних.
А может быть вообще так:
Только одна общая касательная.
И снова факты:
Длины отрезков двух внутренних общих касательных равны
Длины отрезков двух внешних общих касательных равны.
НО! При этом: внешние и внутренние касательные – разные! (а некоторых, может, и вообще нет…)
Касающиеся окружности
Касание окружностей бывает внешним и внутренним.
Вот такая картинка называется «окружности касаются внешним образом»:
А вот такая картинка называется «окружности касаются внутренним образом»:
Что же самое главное нужно знать?
Если две окружности касаются, то точка касания лежит на прямой, соединяющей центры. Кроме того, эта прямая перпендикулярна касательной, проведённой в точку касания окружностей.
Если тебе показалось слишком длинно – посмотри картинку. Может быть ещё так:
Ура, теперь ты полностью вооружён на борьбу с касательными – дерзай! 🙂
Что такое касательная к окружности
Определение. Касательная к окружности — это прямая на плоскости, имеющая ровно одну общую точку с окружностью.
Вот парочка примеров:
Окружность с центром O касается прямой l в точке A 
Из любой точки M за пределами окружности можно провести ровно две касательных 
Различие между касательной l, секущей BC и прямой m, не имеющей общих точек с окружностью
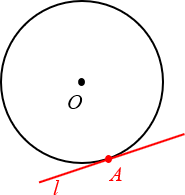
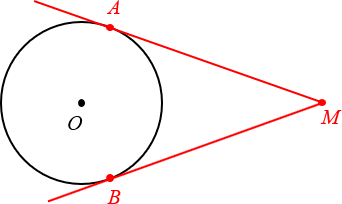
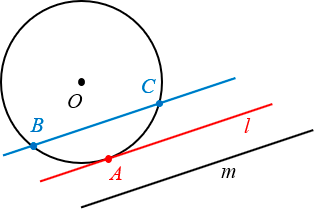
На этом можно было бы закончить, однако практика показывает, что недостаточно просто зазубрить определение — нужно научиться видеть касательные на чертежах, знать их свойства и вдобавок как следует попрактиковаться в применении этих свойств, решая реальные задачи. Всем этим всем мы сегодня и займёмся.
Основные свойства касательных
Для того, чтобы решать любые задачи, нужно знать четыре ключевых свойства. Два из них описаны в любом справочнике / учебнике, а вот последние два — про них как-то забывают, а зря.
1. Отрезки касательных, проведённых из одной точки, равны
Чуть выше мы уже говорили про две касательных, проведённых из одной точки M. Так вот:
Отрезки касательных к окружности, проведённых из одной точки, равны.
Отрезки AM и BM равны
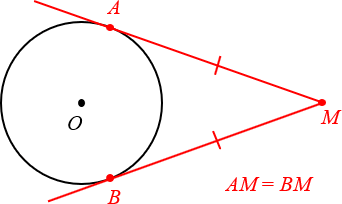
2. Касательная перпендикулярна радиусу, проведённому в точку касания
Ещё раз посмотрим на картинку, представленную выше. Проведём радиусы OAи OB, после чего обнаружим, что углы OAMи OBM — прямые.
Радиус, проведённый в точку касания, перпендикулярен касательной.
Этот факт можно использовать без доказательства в любой задаче:
Радиусы, проведённые в точку касания, перпендикулярны касательным
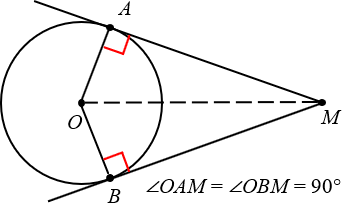
Кстати, заметьте: если провести отрезок OM, то мы получим два равных треугольника: OAM и OBM.
3. Соотношение между касательной и секущей
А вот это уже факт посерьёзнее, и большинство школьников его не знают. Рассмотрим касательную и секущую, которые проходят через одну и ту же общую точку M. Естественно, секущая даст нам два отрезка: внутри окружности (отрезок BC — его ещё называют хордой) и снаружи (его так и называют — внешняя часть MC).
Произведение всей секущей на её внешнюю часть равно квадрату отрезка касательной
Соотношение между секущей и касательной
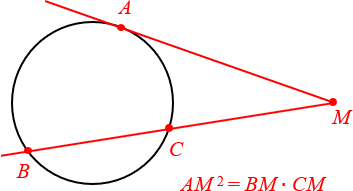
4. Угол между касательной и хордой
Ещё более продвинутый факт, который часто используется для решения сложных задач. Очень рекомендую взять на вооружение.
Угол между касательной и хордой равен вписанному углу, опирающемуся на эту хорду.
Откуда берётся точка B? В реальных задачах она обычно «всплывает» где-то в условии. Поэтому важно научиться распознавать данную конфигурацию на чертежах.
Иногда всё-таки касается 🙂
Общие сведения
Важно знать терминологию, соотношения и теоремы для решения задач этого класса. Касательной к окружности называется прямая, которая имеет с ней только одну точку соприкосновения. Прямая — это линия, не имеющая границ, т. е. она ничем не ограничена. Окружностью называется геометрическое место точек, удаленных от центра на одинаковые расстояния.
Следует отметить, что касательные бывают внешними и внутренними. Внешней называет прямая линия, проходящая с внешней стороны окружности. Внутренние касательные пересекают отрезок, который соединяет центры двух окружностей. Последний тип прямых не существует, когда два круга пересекаются. Касательные нужно уметь правильно строить, поскольку от этого зависит правильность решения задачи.
Построение касательных
Для построения касательной к окружности следует на последней отметить произвольную точку. Затем необходимо через нее провести прямую. Нужно отметить, что у круга может быть несколько таких прямых. Когда даны две окружности, тогда можно проводить не только внешние, но и внутренние. Существует определенный алгоритм, по которому можно построить первый тип:
Существует более простая модель построения таких прямых. Для этого следует начертить один круг, а затем отметить две произвольные точки на его противоположных сторонах. Далее начертить II круг, превышающий I по радиусу. Отметить на нем точки, воспользовавшись подобием, т. е. они должны быть в тех же местах, что и на I. Затем провести прямые, которые должны соприкасаться с I и II кругами только в одной точке.
Для построения внутренних касательных существует определенная методика. В интернете можно найти много информации. В одних источниках алгоритм построения является сложным, а в других — простым. Однако есть один метод, позволяющий осуществить данную операцию. Специалисты описали его на «понятном» языке для новичков. Суть методики заключается в следующем:
Далее нужно рассмотреть некоторые свойства, на основании которых можно решать задачи и доказывать геометрические тождества.
Основные свойства
Свойства — утверждения, полученные в результате доказательства теорем о касательной к окружности. Первые нет необходимости доказывать, поскольку об этом уже позаботились математики. Они выделяют всего 4 свойства касательных к окружности:
Для рассмотрения I свойства необходимо начертить окружность с центром О1. Затем нужно отметить точку М вне окружности. Из М провести одну прямую, которая соприкасается с кругом в точке А. Такую же операцию следует проделать и для другой касательной. Точку соприкосновения назвать В. Отрезки АМ и ВМ равны между собой.
Если провести радиусы к точкам А и В, то можно сделать вывод, что углы являются прямыми. Чтобы понять третье свойство, необходимо начертить окружность и отметить некоторую точку М за ее пределами. После этого следует из искомой точки провести секущую и касательную. Первой называется прямая, проходящая через окружность и пересекающая ее в двух точках. Для касательной точку соприкосновения необходимо обозначить А. Тогда секущая пересекает круг в точках В (ближняя) и С (дальняя). В результате этого получается такое соотношение: АМ 2 = АВ * МС.
Когда для произвольной окружности существуют касательная и секущая, тогда между ними образуется некоторый угол.
Хорда, полученная в результате прохождения через окружность, образует также угол. Он опирается на искомую хорду и является вписанным. Следовательно, по свойству градусные меры углов равны между собой. Далее нужно разобрать частные случаи, на основании которых можно сделать вывод о количестве касательных.
Когда окружность вписана в ромб, тогда их точки касания нужно рассматривать по первому свойству. Радиус окружности можно найти по следующим формулам:
Следует отметить, что у ромба две диагонали. Они различаются по размеру. Одна из них больше другой (d1 > d2).
Частные случаи
В некоторых задачах нужно определить количество касательных у двух окружностей. Можно выполнить ряд сложных и трудоемких доказательств. В результате этого будет потрачено много времени, а можно воспользоваться уже готовыми дополнительными свойствами:
Когда заданы окружности, радиус одной из которых равен 0, тогда «нулевой» круг эквивалентен двойной точке. Прямая является двойной и проходит через эту точку. В этом случае математики определяют всего две внешних. Если r1 = r2 = 0, то всего 4 внешних общих касательных. Далее для решения задач нужно разобрать доказательства некоторых свойств.
Доказательства утверждений
Очень важно знать доказательства некоторых свойств и теорем, поскольку одним из типов задач считаются упражнения повышенной сложности, требующие логических расчетов в общем виде. Например, нужно доказать, что касательная образует с радиусом, проведенным к точке касания, прямой угол. Существует тип доказательства от противного.
Следует отметить, что уравнение окружности с радиусом, равным единице, описывается функцией x 2 + y 2 = 1. Эта запись применяется для решения задач в общем виде. Прямая — функция, описанная прямой пропорциональностью у = кх + b. Чтобы связать окружность и касательные, нужно составить систему уравнений. Этот математический ход объясняется тем, что у функций должны быть общие решения (точка на окружности). После решения можно выполнить проверочные вычисления, подставив корни в систему.
Таким образом, для решения задач об окружности и касательной следует знать общие понятия, а также основные свойства и теоремы.