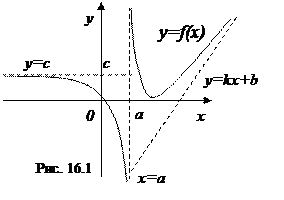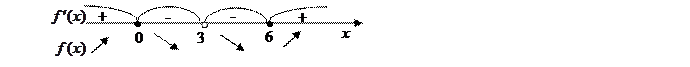что такое наклонная асимптота графика функции

Асимптота графика функции: определение, как искать

Что такое асимптота — понятие и определение

Асимптота графика функции у=f (x) представляет собой прямую L, максимально приближающеюся к графику функции, точка которого стремится к бесконечности, то есть неограниченно удаляется от начала координат по кривой. Расстояние между этой точкой функции у=f(x) и асимптотой L стремится к нулю.

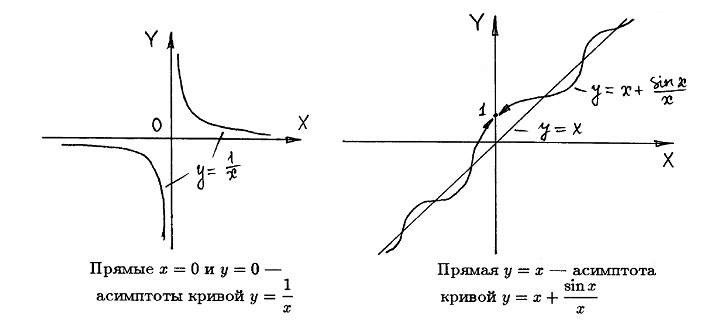
На рисунке приведены примеры асимптот графиков функций.

На рисунке слева продемонстрирована кривая, которая приближается к асимптоте и остается с одной стороны по отношению к ней.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

На рисунке справа представлена кривая (график функции), которая пресекает асимптоту бесконечное множество раз с разных сторон

Асимптоты графика функции, основные виды

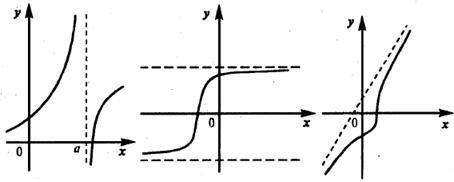
Асимптоты делятся на три вида: вертикальные, наклонные и горизонтальные.

У разных функции в наличии может быть различное количество асимптот:

Приведем пример нахождения асимптот гиперболы.

Гипербола — геометрическое место расположения точек, от которых абсолютная величина разности растояний до двух фокусов (заданных точек), является постоянной и меньшей, чем расстояние между самими фокусами.

Это действительно, так как:

Следовательно, если абсцисса х неограниченно возрастает, то график гиперболы и ее асимптота неограниченно сближаются.

Расположение асимптот гиперболы соответствует диагоналям прямоугольника, стороны которого параллельны оси Ох и оси Оу, а центром служит начало координат.

Пример

Необходимо составить уравнение гиперболы, если следующие уравнения задают ее асимптоты:

Решение

Применим формулу \(y=\frac bax\) и получим:

Подставим координаты точки М в общую формулу уравнения гиперболы:

Получим систему уравнений. Чтобы получить уравнение данной гиперболы, необходимо вычислить полученную систему уравнений.

Вертикальные асимптоты

Если хотя бы один из пределов \(\lim_f(x)\) или \(\lim_f(x)\) является равным +∞ или —∞, то вертикальной асимптотой графика функции у=f(x) будет являться прямая х=с.

Примеры вертикальных асимптот:

Пример 1

Необходимо определить вертикальную асимптоту функции \(\lim_a(x)=0.\)

Решение

то x=0 — вертикальная асимптота.

Пример 2

Ось ординат является вертикальной асимптотой, так как

Наклонные асимптоты

Если в определении асимптоты присутствует +∞ или —∞, то она относится либо к горизонтальной, либо к наклонной.

Если k=0, то наклонная асимптота превращается в горизонтальную.

Применение правила Лопиталя

Правило Лопиталя применяется, когда границы не определены, например, 0/0 или ∞/∞:

Если функции можно дифференцировать, и они относятся к окрестностям точки x=a, тогда наклонную асимптоту необходимо искать по формуле:

Производная может применяться многократно для получения константы в числителе или знаменателе.

Пример 1

Прямая у=х — наклонная асимптота графика данной функции.

Пример 2

Рассмотрим два варианта:

То есть правая ветвь кривой имеет наклонную асимптоту в виде прямой у=х-2.

То есть левая ветвь кривой имеет наклонную асимптоту в виде прямой у=-х+2.

Горизонтальные асимптоты

Прямая y=b является горизонтальной асимптотой для графика функции y=f(x), если

Пример 1

Имеется функция: \(y=4+\frac1x.\)

поэтому y=4 — горизонтальная асимптота данной функции.

Пример 2

Значит, у=1 — горизонтальная асимптота графика функции.

Пример 3

Источник

Что такое наклонная асимптота графика функции

Нахождение асимптот графика функции основано на следующих утверждениях.

Таким образом, вертикальные асимптоты графика функции следует искать в точках разрыва функции или на концах ее области определения (если это конечные числа).

Заметим, что если хотя бы один из указанных пределов бесконечен, то наклонной асимптоты нет.

Наклонная асимптота так же, как и горизонтальная, может быть односторонней.

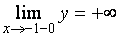
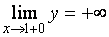
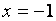
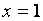
Так как и (два других односторонних предела можно уже не находить), то прямые и являются вертикальными асимптотами графика функции.

(применим правило Лопиталя ) =

Так как горизонтальная асимптота существует, то наклонные уже не ищем (их нет).

Источник

Асимптоты графика функции

Асимптотой графика функции y = f(x) называется прямая, обладающая тем свойством, что расстояние от точки (х, f(x)) до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.

На рисунке 3.10. приведены графические примеры вертикальной, горизонтальных и наклонной асимптот.

Нахождение асимптот графика основано на следующих трех теоремах.

Теорема о вертикальной асимптоте. Пусть функция у = f(х) определена в некоторой окрестности точки x₀ (исключая, возможно, саму эту точку) и хотя бы один из односторонних пределов функции равен бесконечности, т.е. Тогда прямая x = x₀ является вертикальной асимптотой графика функции у = f(х).

Очевидно, что прямая х = х₀ не может быть вертикальной асимптотой, если функция непрерывна в точке х₀, так как в этом случае . Следовательно, вертикальные асимптоты следует искать в точках разрыва функции или на концах ее области определения.

Теорема о горизонтальной асимптоте. Пусть функция у = f(х) определена при достаточно больших х и существует конечный предел функции . Тогда прямая у = b есть горизонтальная асимптота графика функции.

Замечание. Если конечен только один из пределов , то функция имеет соответственно левостороннюю либо правостороннююгоризонтальную асимптоту.

В том случае, если , функция может иметь наклонную асимптоту.

Теорема о наклонной асимптоте. Пусть функция у = f(х) определена при достаточно больших х и существуют конечные пределы . Тогда прямая y = kx + b является наклонной асимптотой графика функции.

Наклонная асимптота, так же, как и горизонтальная, может быть правосторонней или левосторонней, если в базе соответствующих пределов стоит бесконечность определенного знака.

Исследование функций и построение их графиков обычно включает следующие этапы:

1. Найти область определения функции.

2. Исследовать функцию на четность-нечетность.

3. Найти вертикальные асимптоты, исследовав точки разрыва и поведение функции на границах области определения, если они конечны.

4. Найти горизонтальные или наклонные асимптоты, исследовав поведение функции в бесконечности.

5. Найти экстремумы и интервалы монотонности функции.

6. Найти интервалы выпуклости функции и точки перегиба.

7. Найти точки пересечения с осями координат и, возможно, некоторые дополнительные точки, уточняющие график.

Дифференциал функции

Можно доказать, что если функция имеет при некоторой базе предел, равный конечному числу, то ее можно представить в виде суммы этого числа и бесконечно малой величины при той же базе (и наоборот): .

Применим это теорему к дифференцируемой функции: .

Отсюда .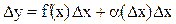

Таким образом, приращение функции Dу состоит из двух слагаемых: 1) линейного относительно Dх, т.е. f `(x)Dх; 2) нелинейного относительно Dх, т.е. a(Dx)Dх. При этом, так как , это второе слагаемое представляет собой бесконечно малую более высокого порядка, чем Dх (при стремлении Dх к нулю оно стремится к нулю еще быстрее).

Дифференциалом функции называется главная, линейная относительно Dх часть приращения функции, равная произведению производной на приращение независимой переменной dy = f `(x)Dх.

Найдем дифференциал функции у = х.

Так как dy = f `(x)Dх = x`Dх = Dх, то dx = Dх, т.е. дифференциал независимой переменной равен приращению этой переменной.

Поэтому формулу для дифференциала функции можно записать в виде dy = f `(x)dх. Именно поэтому одно из обозначений производной представляет собой дробь dy/dх.

Таким образом, дифференциал функции есть приращение ординаты касательной, проведенной к графику функции в данной точке, когда х получает приращение Dх.

Свойства дифференциала в основном аналогичны свойствам производной:

Однако, существует важное свойство дифференциала функции, которым не обладает ее производная – это инвариантность формы дифференциала.

Из определения дифференциала для функции y = f(x) дифференциал dy = f `(x)dх. Если эта функция y является сложной, т.е. y = f(u), где u = j(х), то y = f[j(х)] и f `(x) = f `(u)*u`. Тогда dy = f `(u)*u`dх. Но для функции
u = j(х) дифференциал du = u`dх. Отсюда dy = f `(u)*du.

Сравнивая между собой равенства dy = f `(x)dх и dy = f `(u)*du, убедимся, что формула дифференциала не изменяется, если вместо функции от независимой переменной х рассматривать функцию от зависимой переменной u. Это свойство дифференциала и получило название инвариантности (т.е. неизменности) формы (или формулы) дифференциала.

Однако в этих двух формулах все же есть различие: в первой из них дифференциал независимой переменной равен приращению этой переменной, т.е. dx = Dx, а во в торой дифференциал функции du есть лишь линейная часть приращения этой функции Du и только при малых Dх du » Du.

Источник

Лекция 16. АСИМПТОТЫ ГРАФИКА ФУНКЦИИ

План:

Одним из важных этапов построения графиков функций является поиск асимптот. С асимптотами мы встречались неоднократно: при построении графиков функций 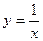, y=tgx, y=сtgx. Мы определяли их как линии, к которым «стремится» график функции, но никогда их не пересечет. Пришло время дать точное определение асимптот.

Асимптоты бывают трех видов: вертикальная, горизонтальная и наклонная. На чертеже асимптоты принято обозначать пунктирными линиями.

Рассмотрим следующий искусственно составленный график функции (рис. 16.1), на примере которого хорошо видны все виды асимптот:

Дадим определение каждому виду асимптот:

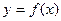
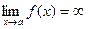
1. Прямая х=а называется вертикальной асимптотой функции , если .

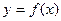
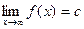
2. Прямая у=с называется горизонтальной асимптотой функции , если .

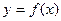
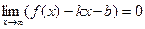
3. Прямая у=kx+b называется наклонной асимптотой функции , если .

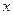
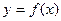
Геометрически определение наклонной асимптоты означает, что при →∞ график функции сколь угодно близко подходит к прямой у=kx+b, т.е. они практически совпадают. Разность практически одинаковых выражений стремится к нулю.

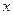
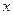
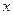
Отметим, что горизонтальные и наклонные асимптоты рассматриваются только при условии →∞. Иногда их различают на горизонтальные и наклонные асимптоты при →+∞ и →-∞.

Для поиска асимптот можно использовать следующий алгоритм:

Вертикальных асимптот может быть одна, несколько или не быть совсем.

Если функция представляет собой отношение двух многочленов, то при наличии у функции горизонтальных асимптот наклонные асимптоты искать не будем – их нет.

Рассмотрим примеры нахождения асимптот функции:

Пример 16.1. Найдите асимптоты кривой .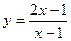

Решение. 1. Найдем область определения функции: х-1≠0; х≠1.

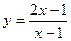
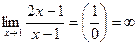
Проверим, является ли прямая х=1 вертикальной асимптотой. Для этого вычислим предел функции в точке х=1: .

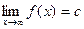
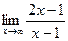
2. Для поиска горизонтальных асимптот находим : с= .

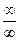
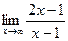
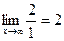
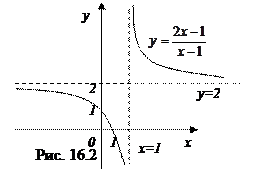
Поскольку в пределе фигурирует неопределенность , воспользуемся правилом Лопиталя: с= = . Т.к. с=2 (число), то у=2 – горизонтальная асимптота.

Так как функция представляет собой отношение многочленов, то при наличии горизонтальных асимптот утверждаем, что наклонных асимптот нет.

Таким образом, данная функция имеет вертикальную асимптоту х=1 и горизонтальную асимптоту у=2. Для наглядности график данной функции представлен на рис. 16.2.

Пример 16.2. Найдите асимптоты кривой .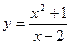

Решение. 1. Найдем область определения функции: х-2≠0; х≠2.

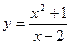
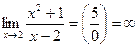
Проверим, является ли прямая х=2 вертикальной асимптотой. Для этого вычислим предел функции в точке х=2: .

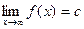
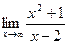
2. Для поиска горизонтальных асимптот находим : с= .

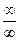
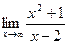
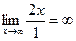
Поскольку в пределе фигурирует неопределенность , воспользуемся правилом Лопиталя: с= = . Т.к. с – бесконечность, то горизонтальных асимптот нет.

3. Для поиска наклонных асимптот находим :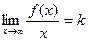

= = = .

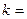
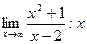
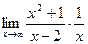
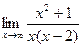
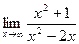
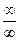
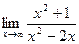
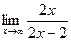
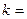
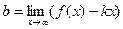
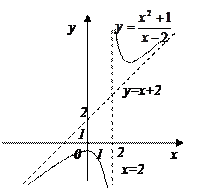
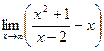
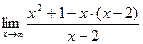
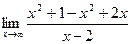
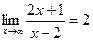
Получили неопределенность вида , воспользуемся правилом Лопиталя: = =1.Итак, 1. Найдем b по формуле: .

b= = =

= = .

Получили, что b= 2. Тогда у=kx+b – наклонная асимптота. В нашем случае она имеет вид: у=x+2.

Таким образом, данная функция имеет вертикальную асимптоту х=2 и наклонную асимптоту у=x+2. Для наглядности график функции 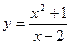представлен на рис. 16.3.

Контрольные вопросы:

Лекция 17. ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ И ПОСТРОЕНИЯ ГРАФИКА

В данной лекции мы подведем итог всему ранее изученному материалу. Конечная цель нашего долгого пути – уметь исследовать любую аналитически заданную функцию и строить ее график. Важными звеньями нашего исследования будут исследование функции на экстремумы, определение интервалов монотонности, выпуклости и вогнутости графика, поиск точек перегиба, асимптот графика функции.

С учетом всех вышеперечисленных аспектов приведем схему исследования функции и построения графика.

1. Найти область определения функции.

2. Исследовать функцию на четность-нечетность:

· если 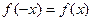, то функция четная (график четной функции симметричен относительно оси Оу);

· если 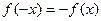, то функция нечетная (график нечетной функции симметричен относительно начала координат);

· в противном случае функция ни четная, ни нечетная.

3. Исследовать функцию на периодичность (среди изучаемых нами функций периодическими могут быть только тригонометрические функции).

4. Найти точки пересечения графика функции с осями координат:

· Ох: у=0 (решаем уравнение лишь в том случае, если можем использовать известные нам методы);

5. Найти первую производную функции и критические точки первого рода.

6. Найти интервалы монотонности и экстремумы функции.

7. Найти вторую производную функции и критические точки второго рода.

8. Найти интервалы выпуклости-вогнутости графика функции и точки перегиба.

9. Найти асимптоты графика функции.

10. Построить график функции. При построении следует учесть случаи возможного расположения графика вблизи асимптот:

вертикальной	горизонтальной	наклонной

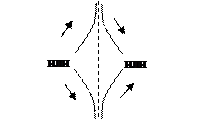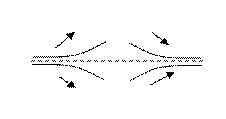11. При необходимости выбрать контрольные точки для более точного построения.

Рассмотрим схему исследования функции и построения ее графика на конкретных примерах:

Пример 17.1. Постройте график функции .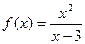

Решение. 1. Данная функция определена на всей числовой прямой за исключением х=3, т.к. в этой точке знаменатель обращается в ноль.

2. Для определения четности и нечетности функции найдем :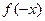

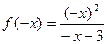
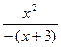
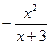
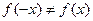
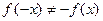
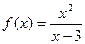
= = . Видим, что и , следовательно, функция ни четная, ни нечетная.

3. Функция непериодическая.

4. Найдем точки пересечения с осями координат. Для нахождения точки пересечения с осью Ох примем у=0. Получим уравнение: 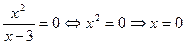. Итак, точка (0; 0) – точка пересечения с осями координат.

5. Найдем производную функции по правилу дифференцирования дроби: = = = = .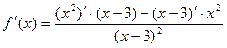

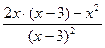
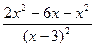
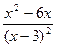
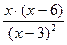
Для нахождения критических точек найдем точки, в которых производная функции равна 0 или не существует.

, если =0, следовательно, . Произведение тогда равно 0, когда хотя бы один из множителей равен 0: или .

не существует, если знаменатель (х-3) 2 равен 0, т.е. не существует при х=3.

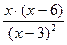
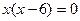
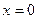
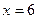
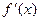
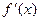
Итак, функция имеет три критические точки первого рода: ; ; .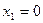

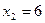
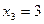
6. На числовой оси отметим критические точки первого рода, причем точку 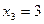отмечаем выколотой точкой, т.к. в ней функция не определена.

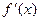
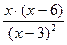
Расставляем знаки производной = на каждом промежутке:

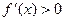
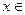
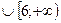
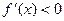
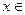
На промежутках, где , исходная функция возрастает (при (-∞;0] ), где — убывает (при [0;3) (3;6]).

Точка х=0 является точкой максимума функции. Для нахождения максимума функции найдем значение функции в точке 0: .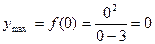

Точка х=6 является точкой минимума функции. Для нахождения минимума функции найдем значение функции в точке 6: .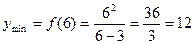

Результаты исследований можно занести в таблицу. Число строк в таблице фиксировано и равно четырем, а число столбцов зависит от исследуемой функции. В ячейки первой строки последовательно заносят интервалы, на которые критические точки разбивают область определения функции, включая сами критические точки. Во избежание ошибок при построении точки, не принадлежащие области определения, можно в таблицу не включать.

Во второй строке таблицы расставляются знаки производной на каждом из рассматриваемых промежутков и значение производной в критических точках. В соответствии со знаками производной функции в третьей строке отмечаются промежутки возрастания, убывания, экстремумы функции.

Последняя строка служит для обозначения максимума и минимума функции.

х	(-∞;0)	(0;3)	(3;6)	(6;+ ∞)
	+	—	—	+
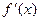f(x)
Выводы	max	min

7. Найдем вторую производную функции как производную от первой производной: = =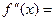

= .

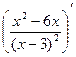
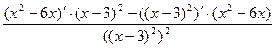
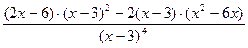
Вынесем в числителе х-3 за скобки и выполним сокращение:

= .

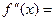
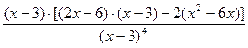
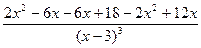
Приведем в числителе подобные слагаемые: .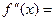

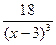
Найдем критические точки второго рода: точки, в которых вторая производная функции равна нулю или не существует.

0, если =0. Данная дробь не может равняться нулю, следовательно, точек, в которых вторая производная функции равна нулю, нет.

не существует, если знаменатель (х-3) 3 равен 0, т.е. не существует при х=3.

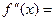
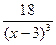
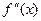
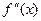
Итак, функция имеет одну критическую точку второго рода: .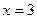

8. Найдем интервалы выпуклости и точки перегиба графика функции.

На числовой оси отметим критическую точку второго рода выколотой точкой, т.к. в ней функция не определена.

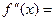
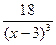
Расставляем знаки второй производной на каждом промежутке:

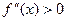
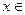
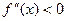
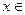
На промежутках, где , исходная функция вогнута (при (3;+∞)), где — выпукла (при (-∞;3)).

Точка х=3 не является точкой перегиба графика функции, т.к. в ней исходная функция не определена.

9. Найдем асимптоты графика функции.

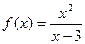
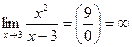
9.1. Поскольку область определения функции – все действительные числа за исключением х=3, то проверим, является ли прямая х=3 вертикальной асимптотой. Для этого вычислим предел функции в точке х=3: .

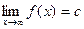
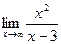
9.2. Для поиска горизонтальных асимптот находим : с= .

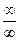
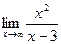
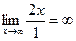
Поскольку в пределе фигурирует неопределенность , воспользуемся правилом Лопиталя: с= = . Т.к. с – бесконечность, то горизонтальных асимптот нет.

9.3. Для поиска наклонных асимптот находим :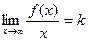

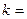
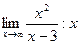
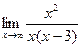
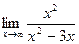
= = =1.

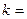
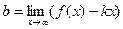
Итак, 1. Найдем b по формуле: .

b= = = = .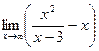

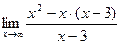
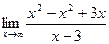
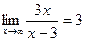
Получили, что b= 3. Тогда у=kx+b – наклонная асимптота. В нашем случае она имеет вид: у=x+3.

Таким образом, данная функция имеет вертикальную асимптоту х=3 и наклонную асимптоту у=x+3.

10. По полученным ранее данным строим график функции (рис. 17.1). Поскольку к построению графика предъявляются высокие требования, система координат должна быть задана корректно: должно присутствовать обозначение осей Ох, Оу, начало отсчета, единицы измерения по каждой оси.

Прежде чем строить график функции, нужно:

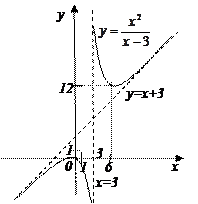
· провести асимптоты пунктирными линиями;

· отметить точки пересечения с осями координат;

·

отметить максимум и минимум функции, причем рекомендуется прямо на чертеже обозначить максимум и минимум функции дугами: k или ;

· пользуясь полученными данными о промежутках возрастания, убывания, выпуклости и вогнутости, построить график функции. Ветви графика должны «стремиться» к асимптотам, но их не пересекать.

· проверить, соответствует ли график функции проведенному исследованию: если функция четная или нечетная, то соблюдена ли симметрия; соответствуют ли теоретически найденным промежутки возрастания и убывания, выпуклости и вогнутости, точки перегиба.

; .

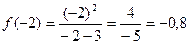
Корректируем график с учетом контрольных точек.

Контрольные вопросы:

ГЛАВА 3. 3. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник