что такое лчм сигнал

Что такое лчм сигнал

Излучаемый активной РЛС сигнал играет роль инструмента исследования пространства радиолокационного наблюдения и называется зондирующим (ЗС).

Известны две наиболее общие формы записи радиосигнала: вещественная и комплексная.

При первой форме ЗС имеет вид

Sз(t) = UmU(t)cos[2pf0t + j(t)], (1)

где: Um – амплитуда излучаемых колебаний;

f0 – несущая частота СВЧ колебаний;

U(t) – закон амплитудной модуляции (огибающая сигнала);

j(t) – закон фазовой модуляции ЗС.

Комплексная форма записи ЗС имеет вид

(2)

где — комплексный закон модуляции ЗС (комплексная огибающая сигнала).

Очевидно, что вещественная форма записи ЗС совпадает с действительной частью ее комплексной формы.

Комплексная форма записи более удобна при математическом описании процессов, чем вещественная, однако необходимо помнить, что физические процессы в радиотехнических цепях (токи и напряжения) описываются вещественными функциями вида (1).

Для описания и анализа ЗС используются их параметры и характеристики: энергетические, временные, частотные и частотно-временные.

Основные энергетические параметры ЗС :

Ри – импульсная мощность;

Рср = Ри/Qc – средняя мощность (Qc =Тп/tи- скважность сигнала);

Эс – энергия сигнала:

для одиночного импульса Эс = Эи = Ри tи;

для пачки импульсов Эс = М Эи (М – количество импульсов в пачке);

К временным параметрам относятся :

tи – длительность импульса;

Тп – период повторения;

Тс = МТп – длительность сигнала (для пачек импульсов).

При временном описании непрерывного сигнала можно рассматривать его как бесконечную последовательность примыкающих друг к другу радиоимпульсов (tи = Тп; Qc = 1).

Частотными параметрами ЗС является:

f0 – несущая частота;

Dfс – ширина спектра сигнала;

Fп = 1/Тп – частота повторения импульсов в пачке для импульсных последовательностей.

(3)

Следует помнить, что спектр комплексного сигнала сам является комплексной функцией и записывается в виде:

, (4)

где — амплитудно-частотный спектр (АЧС) ЗС, характеризующий распределение амплитуд гармонических составляющих его спектра;

— фазо-частотный спектр (ФЧС) ЗС, характеризующий распределение начальных фаз гармонических составляющих полного спектра.

Другой важнейшей, с точки зрения радиолокации, характеристикой ЗС является нормированная двумерная автокорреляционная функция (АКФ) ( нормированная функция неопределенности сигнала ) закона модуляции:

, (5)

где U*(t) – комплексно сопряженная функция к U(t).

Физический смысл (5) заключается в том, что она характеризует степень связи (корреляцию) ЗС с его копией смещенной по времени и частоте. В прямоугольной системе координат функция представляет собой поверхность тела неопределенности сигнала.

Важность функции (5) заключатся в том, что она описывает комплексную огибающую сигнала на выходе любого оптимального радиолокационного приемника. Она определяет такие важнейшие характеристики РЛС как качество обнаружения, разрешающую способность по дальности Д и скорости V, точность измерения координат и помехозащищенность станции.

Основные свойства АКФ.

Первое свойство состоит в том, что принимает максимальное значение, равное 1, при t = F = 0.

Второе свойство состоит в симметрии этой функции относительно аргументов: = .

При отсутствии частотного рассогласования (F = 0), выражение (5) характеризует связь закона модуляции с его копией, отличающейся лишь временным сдвигом

(6)

В случае если сигнал и его копия совпадают по времени (t = 0) выражение (5) приобретает вид

(7)

и характеризует нормированный АЧС квадрата модуля огибающей сигнала.

Как правило, для анализа свойств ЗС нет необходимости строить и рассматривать все тело неопределенности, достаточно построить его сечения плоскостями F = 0, t = 0 и проекцию постоянного уровня, например, r = 0,5.

5.4.2. Непрерывный ЗС

Для обнаружения целей на малых и предельно малых высотах (менее 1 километра) в условиях интенсивных отражений от местных предметов и подстилающей поверхности целесообразно использовать непрерывные ЗС, так как они обеспечивают максимальную потенциальную защищенность РЛС от этих видов помех.

Немодулированный непрерывный сигнал ( монохроматический ) единичной амплитуды в комплексной форме может быть представлен в виде

,

Двумерная нормированная АКФ такого сигнала равна

.

АКФ непрерывного немодулированного сигнала является функцией, не зависящей от временного сдвига t и обращающийся в ноль всюду, кроме плоскости F = 0.

Измерение дальности немодулированным непрерывным ЗС невозможно. Однако потенциально такой сигнал позволяет проводить измерения и разрешать цели по радиальной скорости с бесконечной точностью.

Например, при круговом сканировании по азимуту луча шириной 1° с частотой вращения 20 оборотов в минуту время облучения несложно рассчитать, оно составляет t обл ≈ 8,3 мс, соответственно ширина спектра D f ≈ 120 Гц.

Поскольку радиальная скорость целей существенно выше скоростей малоподвижных или неподвижных источников мешающих отражений, использование непрерывного ЗС позволяет с высокой эффективностью осуществлять селекцию (различение) полезных сигналов.

Непрерывный ЗС позволяет эффективно решать задачи обнаружения и сопровождения целей на фоне мешающих отражений, превышающих по интенсивности полезный сигнал на 60-80 Дб.

5.4.3. Простой прямоугольный радиоимпульс

Импульсные сигналы используются, как правило, для обзора пространства и подразделяются в свою очередь на одиночные радиоимпульсы (РИ) и последовательности импульсов. В зависимости от внутриимпульсной модуляции одиночные РИ делятся на простые, то есть немодулированные и ЛЧМ РИ, то есть с внутриимпульсной линейной частотной модуляцией.

Простой прямоугольный радиоимпульс с нулевой начальной фазой имеет огибающую вида

(1)

где 1(t) – единичная функция.

Радиоимпульс единичной амплитуды может быть представлен в виде

.

Нормированная двумерная АКФ такого сигнала описывается зависимостью

, при . (2)

Вид тела неопределенности, заданного выражением (2), представлен на рисунке 1.

Рис. 1. Тело неопределенности простого прямоугольного радиоимпульса.

АКФ сигнала – , есть сечение двумерной АКФ плоскостью F = 0

(2)

Рис. 2. АКФ простого прямоугольного радиоимпульса

Аналогичным образом можно получить сечения тела неопределенности для любых фиксированных F. Характерные случаи показаны на рисунке 2.

Как следует из рис. 2, время корреляции t к простого радиоимпульса совпадает с длительностью импульса.

Условие разрешения двух целей по дальности (разрешающая способность):

. (3)

Нормированный АЧС квадрата модуля огибающей сигнала – то есть сечение двумерной АКФ плоскостью t = 0

. (4)

Рис. 3. Нормированный АЧС квадрата модуля огибающей сигнала

Характер изменения при выборе различных t = const виден из рис.2.

Ширина функции по уровню 0,5 является мерой разрешения сигнала по частоте и составляет величину, обратную длительности импульса

.

Условие разрешения двух целей по доплеровской частоте (разрешающая способность):

.

Чтобы оценить поведение АКФ при одновременном рассогласовании по F и t применяют проекции постоянных уровней, приведенные на рис. 4

Рис. 4. Проекции постоянных уровней r(t,F)

5.4.4. Линейно-частотно модулированный (ЛЧМ) радиоимпульс

Радиоимпульс с линейной частотной модуляцией (ЛЧМ) является сложным сигналом, база которого больше 1.

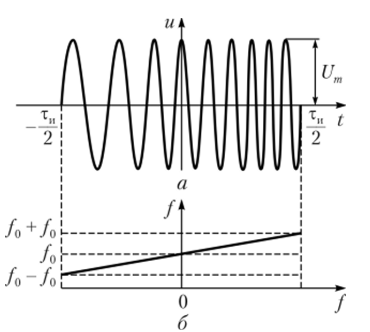
ЛЧМ радиоимпульс (рис. 1) представляет собой сигнал, у которого в течение длительности импульса tи частота изменяется по линейному закону

, (1)

где Dfд – девиация частоты.

Рис. 1. Закон изменения частоты ЛЧМ радиоимпульса

Фаза такого сигнала изменяется по квадратичному закону от времени

,

а комплексная огибающая может быть представлена в виде

.

где b = pn/ — параметр фазовой модуляции;

n = — база сигнала.

Энергетические параметры ЛЧМ сигнала (Ри, Эс) с прямоугольной огибающей не зависят от закона внутриимпульсной модуляции и совпадает с параметрами простого прямоугольного радиоимпульса.

АЧС прямоугольного ЛЧМ радиоимпульса для n ³ 50 изображен на рис. 6.

Рис. 2. АЧС прямоугольного ЛЧМ импульса

Из рисунка видно, что форма огибающей спектра приближается к прямоугольной, а ширина определяется девиацией частоты сигнала.

Нормированная двумерная АКФ рассматриваемого сигнала определяется выражением

Рельеф этой функции приведен на рисунке 3. Тело неопределенности ЛЧМ радиоимпульса отличается от аналогичного тела простого РИ тем, что оно повернуто вокруг оси r на некоторый угол, величина которого пропорциональна частотной девиации. Поворот тела по часовой стрелке соответствует случаю роста частоты, против часовой стрелки – ее убыванию.

Время корреляции сигнала tк характеризуется шириной сечения тела неопределенности плоскостью F = 0 по уровню r = 0,5 и составляет

.

То есть время корреляции ЛЧМ импульса в n раз меньше соответствующего времени простого прямоугольного импульса той же длительности. Следовательно, ЛЧМ сигнал способен обеспечить в n раз лучшую разрешающую способность по дальности, чем простой радиоимпульс.

Рис. 3. Двумерная АКФ ЛЧМ радиоимпульса

Как видно из рисунка 3 частотная расстройка приводит к уменьшению амплитуды АКФ и смещению ее временного положения. Уменьшение амплитуды происходит по треугольному закону, а временное смещение по абсолютной величине составляет . Смещение временного положения АКФ при частотной расстройке характеризует скоростную ошибку при измерении времени запаздывания. Она может оказаться существенной, если максимальное значение в интервале возможных доплеровских частот существенно превосходит величину 1/tи ЛЧМ сигнала, что характерно для импульсов сравнительно большой длительности.

5.4.5. Когерентная пачка прямоугольных радиоимпульсов

(Когерентной называют последовательность радиоимпульсов с одинаковыми или изменяющимися по известному закону начальными фазами.)

Построение тела неопределенности реальной КППРИ (М>500) вызывает определенные вычислительные трудности, поэтому для анализа ее АКФ целесообразно воспользоваться сечениями автокорреляционной функции плоскостями F = const, t = const и проекциями постоянного уровня.

На рисунке 1 изображены огибающие несмещенной и смещенной по времени на величину t пачек из четырех импульсов (М = 4). Поскольку полная длительность сигнала равна МТп, а ширина его спектра определяется величиной DF = 1/tи база такого сигнала равна n = MTпDF = MTп/tи >> 1, а сам сигнал следует признать сложным широкополосным сигналом.

Рис. 1. Огибающие импульсов пачек несмещенного и смещенного сигналов

Из рисунка видно, что если сигналы U(t) и U(t-t) взаимно сдвинуты на величину kTп + tи МТп.

При F = 0 функция r(t) представляет собой последовательность АКФ одиночных прямоугольных радиоимпульсов, то есть каждый пик r(t) и огибающая всех пиков имеют треугольную форму (рис. 2).

Рис. 2. Функция r(t) для КППРИ

Наличие большого числа пиков функции r(t) приводит к неоднозначности в определении дальности до цели, если выполняется условие . Неоднозначность в измерении дальности проявляется в том, что измеренное время задержки t з изм может отличаться от истинного

t з ист на целое число периодов повторения

t з ист = t з изм ± mТп, (1)

где m = 0¸ М априорно неизвестное целое число.

Для устранения указанной неоднозначности может быть использован метод нониусных частот, подразумевающий использование двух КППРИ, отличающихся периодами повторения импульсов в пачке. Подробно этот метод будет рассмотрен на последующих занятиях.

Рассмотрим поведение функции r(t,F) при t = 0. В этом случае r(F) описывает амплитудно-частотный спектр огибающей когерентной пачки радиоимпульсов, который, как известно, является гребенчатым, то есть состоит из целого ряда пиков на частотах кратных частоте повторения импульсов в пачке Fп = 1/Тп. Вид спектра приведен на рисунке 3.

Рис. 3. Амплитудно-частотный спектр огибающей КППРИ

Форма пиков, как и форма огибающей пиков, определяется соотношением вида ½sinx/x½, что следует из выражения (1). Однако, если ширина пика определяется длительностью сигнала tс = МТп, то ширина огибающей пиков определяется длительностью импульса tи.

Из рассмотренного следует, что функция неопределенности КППРИ состоит из рядов сравнительно узких пиков, распределенных как по оси t, так и по оси F. Ее рельеф с помощью проекций постоянных уровней изображен на рисунке 4.

Рис. 4. Проекции постоянных уровней АКФ КППРИ

Сравнение функций неопределенности одиночных и пачечных сигналов при одинаковой длительности импульса показывает, что пачечные сигналы обеспечивают существенно большую разрешающую способность по частоте (радиальной скорости):

.

Из рисунков 3 и 4 видно, что квазинепрерывному сигналу свойственны не только неоднозначность в определении дальности, но и неоднозначность в определении скорости:

,

где — истинное значение радиальной скорости,

— измеренное значение радиальной скорости.

При этом зона однозначного определения обеих координат ограничена одной величиной Tп, поэтому устранение неоднозначности по одной координате, приводит к усилению неоднозначности по другой. Например, можно обеспечить однозначное измерение радиальной скорости, задав частоту повторения примерно 100 килогерц, однако при этом диапазон однозначного измерения дальности не превысит единиц километров.

5.4.6. Импульсные последовательности для связи с ЗУР

Для сопровождения ЗУР используются ограниченные во времени последовательности импульсов, которые принято называть «пачками» запросных импульсов, когерентность которых при обработке не учитывается.

Другим вариантом импульсной последовательности, используемой при работе с ЗУР, является частотно-модулированная последовательность. Она используется для обмена цифровой информацией между ЗУР и РЛС и по существу является не радиолокационным, а связным сигналом.

Источник

Теория радиоволн: аналоговая модуляция

Амплитудная модуляция

При амплитудной модуляции, огибающая амплитуд несущего колебания изменяется по закону, совпадающему с законом передаваемого сообщения. Частота и фаза несущего колебания при этом не меняется.

Одним из основных параметров АМ, является коэфициент модуляции(M).
Коэффициент модуляции — это отношение разности между максимальным и минимальным значениями амплитуд модулированного сигнала к сумме этих значений(%).
Проще говоря, этот коэффициент показывает, насколько сильно значение амплитуда несущего колебания в данный момент отклоняется от среднего значения.
При коэффициенте модуляции больше 1, возникает эффект перемодуляции, в результате чего происходит искажение сигнала.

Данный спектр свойственен для модулирующего колебания постоянной частоты.

На графике, по оси Х представлена частота, по оси У — амплитуда.
Для АМ, кроме амплитуды основной частоты, находящейся в центре, представлены также значения амплитуд справа и слева от частоты несущей. Это так называемые левая и правая боковые полосы. Они отнесены от частоты несущей на расстояние равное частоте модуляции.
Расстояние от левой до правой боковой полосы называют ширина спектра.
В нормальном случае, при коэффициенте модуляции

Источник

Генерирование линейной частотной модуляции (ЛЧМ) радиоимпульсов

Генерирование ЛЧМ радиоимпульсов с помощью генераторов AnaPico RFSG и RFSU серии.

Сигналы с ЛЧМ импульсной модуляцией (ЛЧМ ИМ) широко используются в радиолокации как зондирующий сигнал, так как в отличие от стандартной импульсной модуляции сигналы ЛЧМ ИМ обеспечивают лучшую разрешающею способность по дальности. Вторым популярным применением ЛЧМ ИМ сигналов является имитация эффекта Доплера, связанного с изменение частоты радиочастотного импульса по причине изменения скорости цели.

Для имитации сигналов ЛЧМ ИМ используют аналоговые или векторные генераторы сигналов, далее комбинируют ИМ и ЧМ модуляции в одном генераторе или некоторые производители имеют отдельную ЛЧМ модуляцию. У решения аналоговых генераторов AnaPico RFSG и RFSU есть два преимущества:

В большинстве случаев параметры ЛЧМ ИМ модуляции или Сhirp mod (иностранная литература) не нормируются, производители нормируют отдельно ЧМ, отдельно ИМ модуляцию и отдельно параметры свипирования и пользователь может только оценочно судить о параметрах ЛЧМ модуляции генератора.

Генераторы AnaPico используют технологии ГУН, что позволяет достигать высокой скорости перестройки частоты и широкой полосы девиации. Высококачественный модулятор позволяет генерировать сигналы с ИМ шириной от 10 нс. Это и есть ключевые слагаемые высоких технических характеристик генераторов AnaPico RFSG6, RFSG12, RFSG20 и RFSU6, RFSU12, RFSU20, RFSU40

В этом кратком обзоре будут 4 темы:

Сигнал с ЛЧМ модуляцией является сигнал частота которого изменяется по линейному закону. Если изменение частоты происходит внутри импульса, то речь идет о ЛЧМ ИМ. Критически важными параметрами являются следующие параметры модуляции:

Наклон является наиболее важной характеристикой так как современные системы РЛС требуют осуществить широкую девиацию частоты в пределах короткого импульса.

Выполнить требования к ЛЧМ модуляции могут генераторы с высокой скоростью перестройки частоты, качественным импульсным модулятором. В качестве решения могут быть использованы аналоговые или векторные генераторы.

В приложениях, где используются ЛЧМ сигналы, очень часто предъявляются высокие требования к фазовому шуму генератора и выходной мощности, что следует учитывать.

В данном обзоре представлены две серии аналоговых генераторов сигнала AnaPico, серия RFSG RFSG2,RFSG4, RFSG6, RFSG12, RFSG20, RFSG26- отличное решение в качестве генераторов сигнала среднего класса и серия генераторов RFSU c моделями RFSU6, RFSU12, RFSU20, RFSU26, RFSU40- генераторы класса Hi-end объединяющие в себе ультра-низкий фазовый шум и сверхбыструю перестройку частоту, модуляцию короткими импульсами.

Рисунок 1: Генераторы сигналов серии RFSG и RFSU

Таблица 1: Модели RFSG2, RFSG4, RFSG6

Таблица 2: Модели RFSG12, RFSG20, RFSG26

Таблица 3: Модели RFSU6, RFSU12, RFSU20, RFSU26, RFSU40

Генераторы сигналов AnaPico поставляются с программным обеспечением для управление прибором через ПК SIGNAL GENERATOR GUI, V.211-версия ПО в данном примере.

Существует два способа установить ЛЧМ модуляцию.

1 Способ: Используя графический интерфейс пользователя генераторов сигнала серии RFSG и RFSU устанавливается режим ЛЧМ модуляции.

Используя вкладу меню MODULATION, пользователь переходит в режим выбора модуляции генератора, выбираем режим CHIRP. В подменю управления ЛЧМ модуляцией (CHIRP) пользователь может настроить нужные параметры.

2 Способ: последовательно задать параметры несущей сигнала, параметры ИМ и параметры ЧМ.

Шаг 1: Установка параметров несущей.

Используя меню вкладки СW, вводится значения частоты, мощности. Пункт меню Low AM Noise позволяет снизить амплитудный шум отключим систему ALC. Кнопка RF OFF вкл/выкл РЧ сигнал.

Шаг 2: Установка параметров Импульсной модуляции

Шаг 3: Установка параметров ЧМ

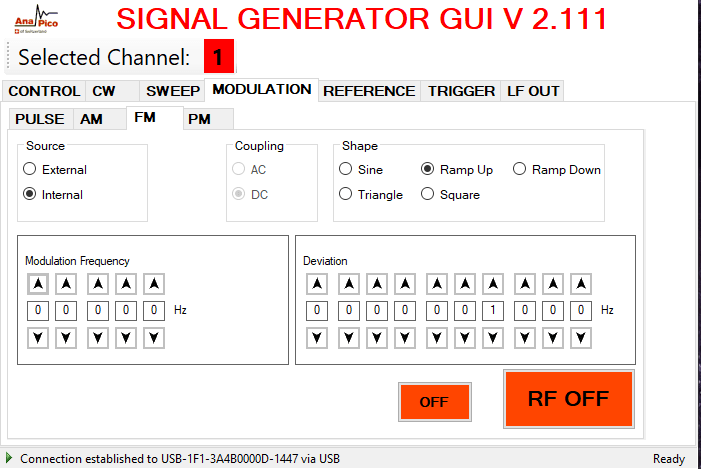
Выбирается вкладка меню FM, для ЛЧМ модуляции устанавливается тип модуляции Ramp UP или Ramp Down, отдельно устанавливаются параметры девиации и частоту модуляции.

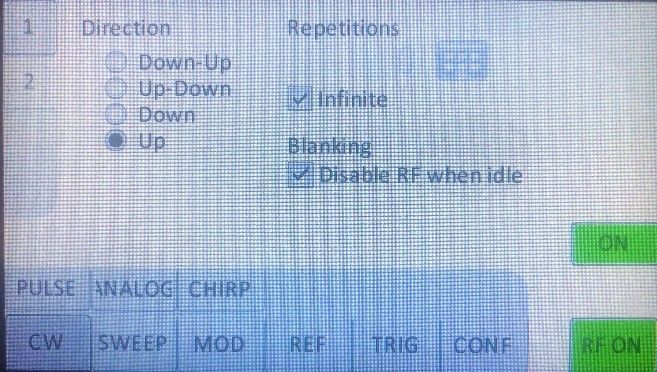
Используя сенсорную переднею панель генератора серии RFSU в меню CHIRP устанавливаем параметры модуляции по аналогии с программным обеспечением AnaPico GUI.

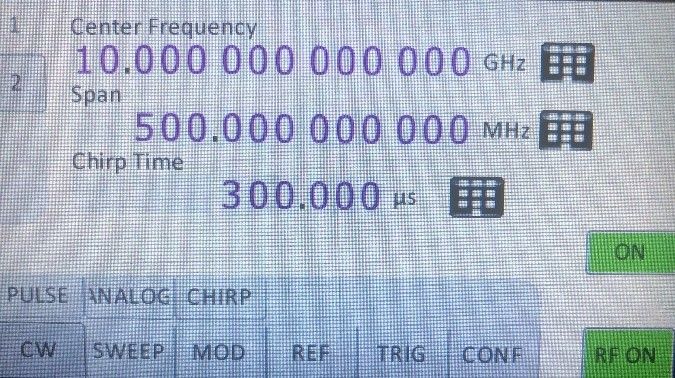
Меню ЛЧМ модуляции имеет две страницы отмеченные 1 и 2, на каждой странице задаются необходимые параметры модуляции.

Кнопка ON-включает модуляцию. Кнопка RF ON включает сигнал несущей частоты.

Заключение:

Генераторы сигналов AnaPico являются универсальным решением для генерирования сигналов с ЛЧМ-модуляцией.

Ключевыми техническими преимуществами решения на основе генераторов AnaPico

Ключевыми не техническими преимуществами являются:

На выбор пользователя предлагается два решения, генераторы сигналов среднего класса

В сочетании с ультра-низким фазовым шумов пользователь генераторов RFSU6, RFSU12, RFSU20, RFSU26, RFSU40 получает качественные параметры импульсной модуляции.

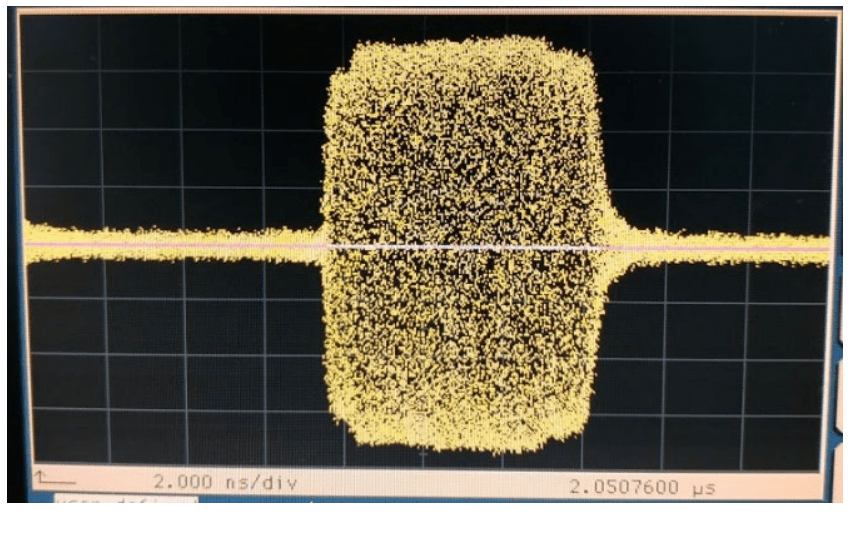
ИМ сигнал на генераторе RFSU40, частота 38.8 ГГц, период 15 нс, длительность 7 нс

Свяжитесь с нами!

Источник