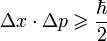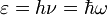что такое квантовая система
Насколько запутанна квантовая система? Ответ может быть невычислим
Фраза «I shit bricks» в статье от Nature — бесценно. Да, это настолько неожиданный результат, что Nature позволяет себе вольности. (от переводчика)

Квантовая запутанность находится в сердце нового математического доказательства.Credit: Victor De Schwanberg/Science Photo Library
Альберт Эйнштейн однажды отметил, что квантовая механика должна позволять двум объектам оказывать влияние друг на друга мгновенно даже на огромных расстояниях, назвав это явление “мистическим дальнодействием” [1]. Спустя десятилетия после его смерти эксперименты подтвердили существование этого явления, но до сих пор остается неясным, насколько скоординированными могут быть объекты в природе. Пять исследователей говорят, что они нашли теоретическое обоснование тому, что ответ в принципе невозможно получить.
Статье на 165 страниц, которую команда выложила на репозиторий препринтов arXiv [2], еще предстоит пройти рецензирование. Если результат подтвердится, он разом решит целый набор связанных проблем в чистой математике, квантовой механике и в теории алгоритмической сложности. В особенности интересно, что он ответит на математический вопрос, остававшийся нерешенным больше 40 лет.
Если доказательство подтвердится, это будет “супер-красивый результат”, как говорит Стефани Вернер, физик-теоретик из Технологического Университета Делфта в Нидерландах.
В сердце статьи находится теорема из теории алгоритмической сложности об эффективности алгоритмов. Предыдущие работы показали, что эта задача математически эквивалентна вопросу о мистическом дальнодействии — которое также называется квантовой запутанностью.
Теорема описывает задачу из теории игр, где команда из двух игроков может координировать свои действия с помощью квантовой запутанности, но при этом не может разговаривать друг с другом. Квантовая запутанность позволяет игрокам выигрывать чаще, чем это было бы возможно в классическом случае. Авторы новой работы доказывают, что игроки принципиально не могут рассчитать оптимальную стратегию игры. Соответственно, невозможно рассчитать, какой степени координации они могут достичь в теории. “Не существует алгоритма, который скажет вам, каково максимальное нарушение классических пределов в квантовой механике” — говорит соавтор Томас Видик из Калтеха.
“Что самое потрясающее, что именно квантовая теория алгоритмической сложности оказалась ключом к доказательству” говорит Тоби Кубитт, специалист по теории квантовой информации из Университетского Колледжа в Лондоне.
Новости о статье быстро разошлись волной воодушевления по социальным сетям после публикации статьи 14 января. “Я думал этот вопрос окажется одним из тех, что требует сотни лет для решения” затвиттил Джозеф Фитцсимонс, исполнительный директор стартапа Horizon Quantum Computing из Сингапура.
“Я тут сру кирпичами” комментирует другой физик, Mateus Araújo из Австрийской Академии Наук в Вене. “Никогда бы не подумал, что в моей жизни увижу решение этой проблемы”.
Наблюдаемые свойства
С точки зрения чистой математики, проблема была известна как задача Конна о вложении, в честь французского математика и лауреата премии Филдса Алана Конна. Это вопрос в теории операторов, области математики, которая сама возникла в 1930х из попыток создать основание для квантовой механики. Операторы это матрицы чисел, которые могут иметь конечное или бесконечное число строк и столбцов. Они играют ключевую роль в квантовой теории, где операторы задают наблюдаемые свойства физических объектов.
В статье 1976 года [3] Конн, используя язык операторов, задавался вопросом: может ли квантовая система с бесконечным числом измеряемых величин быть приблизительно описана более простой системой с конечным числом величин.
Но статья Видика и соавторов доказывает, что ответ — нет: в принципе могут существовать квантовые системы, которые нельзя приблизительно описать конечными системами. Согласно работе физика Бориса Цирельсона [4], который переформировал задачу, это также значит, что невозможно посчитать количество корреляции, которые две такие системы проявят, будучи запутанными.
Несоизмеримые области
Доказательство оказалось сюрпризом для сообщества.”Я был уверен, что проблема Цирельсона должна иметь положительный ответ” написал Araújo в своем комментарии, добавляя, что результат пошатнул его убеждённость в том, что “Природа в некотором смысле фундаментально конечна”.
Но исследователи только начали осознавать все последствия результата. Квантовая запутанность находится в самом сердце зарождающейся области квантовых вычислений и квантовых коммуникаций и может быть использована для создания супер-защищенных сетей. В частности, измерение количества корреляции между запутанными объектами в системе сообщения может дать доказательство надежности сети от прослушивания. Но, как говорит Венер, новый результат вряд ли будет иметь последствия для технологии, так как все практические применения используют конечные квантовые системы. На самом деле, говорит она, даже сложно представить, как должен выглядеть эксперимент, проверяющий квантовую странность бесконечной системы.
Сочетание теории сложности, квантовой информации и математики значит, что лишь немногие ученые могут похвастаться тем, что они понимают все грани новой статьи. Сам Конн сказал Nature, что он не достаточно квалифицирован, чтобы давать комментарий. Но он также добавил, что он удивлен количеством последствий этого результата. “Потрясающе, что эта проблема оказалась столь глубока, я никогда не мог предположить этого!”
Литература
От переводчика
Очень советую почитать пост Скотта Ааронсона про этот результат, в нем много подробностей, особенно полезны комментарии.
А еще о проблеме Цирельсона есть очень интересная презентация, где сама задача рассматривается очень подробно.
И напоследок: если хотите понаблюдать за моими попытками разобраться в том, как вести научный твиттер, добро пожаловать: @hbar_universe.
Квантовая теория открытых систем
Открытая система в квантовой механике — квантовая система, которая может обмениваться энергией и веществом с внешней средой. В определенном смысле всякая квантовая система может рассматриваться как открытая система, поскольку измерение любой динамической величины (наблюдаемой) связано с конечным необратимым изменением квантового состояния системы. Поэтому в отличие от классической механики, в которой измерения не играют существенной роли, теория открытых квантовых систем должна включает в себя теорию квантовых измерений.
Открытые системы в статистической механике и в квантовой механике могут быть гамильтоновыми и негамильтоновыми. Эволюция гамильтоновых систем целиком определяется ее гамильтонианом. Например, в равновесной статистической механике системы с переменным числом частиц, которые можно считать открытыми, описываются большим каноническим распределением Гиббса. Важным классом открытых систем является класс негамильтоновых систем. Именно в негамильтоновых системах возможны процессы самоорганизации. Среди негамильтоновых систем выделяются диссипативные, аккретивные, обобщенно диссипативные системы.
Динамика гамильтоновой квантовой системы, описывается однопараметрической группой унитарных операторов. В качестве уравнений движения используются уравнение фон Неймана и уравнение Гейзенберга. Эволюция негамильтоновой системы, подверженной внешним воздействиям, будь то процесс установления равновесия с окружающей средой или взаимодействие с измерительным прибором, обычно описывается вполне положительными отображениями. Динамика негамильтоновых открытых квантовых систем, обладающих свойством марковости, задается уравнение Линдблада.
Содержание
Примечания
Литература
Литература на русском языке
См. также
Теория струн — Теория суперструн Теория … Википедия
Квантовая механика — Квантовая механика … Википедия
Квантовая механика — волновая механика, теория устанавливающая способ описания и законы движения микрочастиц (элементарных частиц, атомов, молекул, атомных ядер) и их систем (например, кристаллов) а также связь величин, характеризующих частицы и системы, с… … Большая советская энциклопедия
КВАНТОВАЯ МЕХАНИКА — (волновая механика), теория, устанавливающая способ описания и законы движения микрочастиц (элем. ч ц, атомов, молекул, ат. ядер) и их систем (напр., кристаллов), а также связь величин, характеризующих ч цы и системы, с физ. величинами,… … Физическая энциклопедия
Квантовая электроника — Квантовая электроника область физики, изучающая методы усиления и генерации электромагнитного излучения на основе явления вынужденного излучения в неравновесных квантовых системах, а также свойств получаемых таким образом усилителей и… … Википедия
Открытая система (квантовая механика) — У этого термина существуют и другие значения, см. Открытая система. Открытая система в квантовой механике квантовая система, которая может обмениваться энергией и веществом с внешней средой. В определенном смысле всякая квантовая система… … Википедия
Открытая система (статистическая механика) — У этого термина существуют и другие значения, см. Открытая система. Открытая система в статистической механике механическая система, которую может обмениваться веществом и энергией с окружающей средой. Открытые системы взаимодействуют с… … Википедия
Квантовая песочница: часть 2

Квантовая песочница: часть 1
Что такое квантовое состояние? Чем обычное состояние отличается от квантового? В какой момент обычное состояние становится квантовым и что будет, если от него отнять квантовости? Оно всё еще будет квантовым или уже превратится в обычное? Оно же только что было квантовым. Наверное, оно стало запутанным, и кот тоже стал запутанным.
В данной статье постараемся ответить на эти вопросы и разобраться в сути квантовой механики.
Цель: написать простую программу, «имитирующую» квантовую эволюцию, чтобы наконец можно было пощупать эти кубиты ручками.
Оглавление:
Что такое обычное «состояние»? Этим термином пользуются так часто, что он начал восприниматься полностью интуитивно.
Часть I: Классическое состояние
Вопрос №1: «Дана частица P, которую можно наблюдать вдоль отрезка
. Что такое состояние частицы P?»
Ответ: Классическое состояние частицы P — число из отрезка.
Внимательного читателя привлечет слово «наблюдать» — как это вообще понимать?
Оказалось, что все это время на участке 
Мы сказали, что состояние частицы — число из отрезка 

А ведь, утверждая, что состояние есть число, мы, получается, подразумеваем именно это. Именно то, что у нас в наличии бесконечно много детекторов. Но ведь это не так. И такого не может быть в принципе.
На практике мы бы разбили отрезок на конечное число сегментов, а в пересечениях поставили бы детекторы, и каждый детектор был бы способен приближенно сообщить, есть ли частица в его окрестности или нет.
То, что было сделано выше называется квантованием. В данном случае мы провели квантование отрезка на сегменты. Квант — неделимая порция чего-либо в рамках используемой модели, абстрактный термин.
Самые интересные явления начинаются именно по той причине, что состояние частицы теперь перестало быть просто числом.
Часть II: Квантовое состояние
Вопрос №2: «Дана частица P, которую можно наблюдать только в окрестности некоторого числа детекторов на отрезке
. Что такое состояние частицы P?»
Ответ: .
Дан отрезок 
Каждый детектор показывает какое-то определенное число, согласно которому мы можем определить, как далеко находится частица от данного детектора.
A — первый детектор, 

B — второй детектор, 

Выдвинем предположение о частице, чтобы как-то ограничить круг наших исследований:
Предположение: Частица одна, она не может просто так взять и клонировать себя.
Из этого предположения следует, что если частица в А, то она не может быть в В, и наоборот.
Или, что то же самое, если 

Теперь рассмотрим «движение» частицы от детектора А к детектору В. Частица была в А ( 




Таким образом, мы описываем состояние частицы с помощью самих детекторов и их показаний. 
Это запись означает, что конфигурация X включает в себя детектор A, показывающий нам число c1, и детектор B, показывающий нам число c2.
Вопрос №2: «Дана частица P, которую можно наблюдать только в окрестности детекторов, расположенных в точках A и B, которые являются квантованием отрезка
на один сегмент
. Что такое состояние частицы P?»
Предположение: Частица одна, она не может взять и просто так клонировать себя.
Ответ: Квантовое состояние частицы P — вектор двумерного гильбертова пространствас базисными векторами A = <1, 0>и B = <0, 1>. При этом этот вектор нормирован на единицу (
), а базисные векторы A и B являются классическими состояниями из вопроса 1. Такие частицы также называют кубитами в силу двумерности базиса. Когда базис трехмерный, частицы называются кутритами и т. д.
Вопрос №2 (обобщенный): «Дана частица P, которую можно наблюдать только в окрестности конечного числа детекторов, расположенных в точках
, которые являются квантованием отрезка на N — 1 сегмент
. Что такое состояние частицы P?»
Предположение: Частица одна, она не может взять и просто так клонировать себя.
Ответ: Квантовое состояние частицы P — вектор N-мерного гильбертова пространствас базисными векторами
. При этом этот вектор нормирован на единицу
, а базисные векторы
являются классическими состояниями из вопроса 1.
Часть III: Кот
Мы вплотную подошли к самым интересным проявлениям квантовой механики. Без сомнения каждый из читателей хоть краем уха слышал о таких терминах, как «квантовая суперпозиция» или «квантовая запутанность» — эти эффекты и другая подобная магия начинаются именно в тот момент, когда вы не будете делать тех умозаключений, которые не требуются.
У нас есть два определения состояния.
Определение №1: Классическое состояние частицы P — число из отрезка
…
Предположение: Частица одна, она не может взять и просто так клонировать себя.
Определение №2: Квантовое состояние частицы P — вектор двумерного гильбертова пространства …
Обычно из каких-то определений выводят следствия, здесь же нас будет интересовать то, что не следует из определения, но мы все равно назовем это следствиями для стройности.
Следствие №1: Из определения квантового состояния не следует, что частица находится в одной точке отрезка. Вообще ниоткуда никак не следует.
То есть частица может находится сразу в двух точках! Например для частицы, которая находится в квантовом состоянии 
Следствие №2: Из определения квантового состояния не следует, что частица разделилась на маленькие кусочки, одни кусочку полетели туда, а другие сюда.
Как это вообще понимать? Как частица может находится сразу в двух точках и при этом оставаться неделимой? Мы же привыкли, что кот Шрёдингера и жив, и мертв одновременно, значит и частица тоже и здесь, и там одновременно. Но ведь она же неделима. Она что растянулась?
Введем понятие роя и экземпляра виртуальных частиц.
Часть IV: Рой
Определение №3: Экземпляр частицы — виртуальный объект, которому соответствует положение в пространстве в данный момент времени, траектория движения с течением времени, а также комплексное число (называемое амплитудой), обладающее модулем и аргументом, для которого справедливы все алгебраические правила:

Определение №4: Рой — совокупность экземпляров.
Определение №5: Частица — рой (при выполнении операции квантования пространства).
Представим экземпляр как шарик, внутри которого есть стрелка, соответствующая комплексному числу в комплексной плоскости. Важно понимать, что шарик может иметь одно направление движения, а стрелка внутри него — другое, то есть эти направления разные.
Но почему разные? Дело в том, что процессы внутри элементарной частицы настолько сложно описать, что влияние этих процессов на движение самой частицы невозможно предсказать на фундаментальном уровне, поэтому и связи между стрелкой внутри шарика и направлением движения самого шарика для нас не существует.
Словесные манипуляция, которые мы сейчас совершили, бесполезны, если не определить законы изменения величин r, φ и закон движения, ведь в них все и упирается.
Закон изменения аргумента: φ постоянно равномерно увеличивается на величину dφ по мере движения экземпляра.
Иными словами, наши комплексное стрелки постоянно крутятся в одном и том же направлении. Зачем это нужно? Чтобы система ни при каких обстоятельствах не перестала эволюционировать.
Закон сложения и умножения: По мере движения вдоль одной траектории амплитуды перемножаются. Амплитуды вдоль всевозможных траекторий складываются.
Данный закон также известен как «принцип суперпозиции в квантовой механике»
| 1. Внутри каждого шарика находится та самая комплексная стрелка, которая крутится на угол dφ после каждого перемещения экземпляра из одной клетки в другую. | 2. Таким образом у нас есть огромная динамическая система, которая постоянно клонирует себя. | 3. Направление движения самого первого экземпляра, в целом, определяет движения роя, но рой тем не менее распространяется во все стороны. Если же отследить движение любого отдельного экземпляра (не обращая внимание на клонов), то он будет двигаться по абсолютно случайной траектории. |
Мы не забываем, что внутри каждого шарика находится комплексная стрелка, которая имеет свое направление и длину. Как предсказать, какая результирующая стрелка окажется в произвольной клетке пространства в данный момент времени? Очевидно, для этого нужно знать, что было со всей системой в предыдущий момент времени. Мы получаем дифференциальное уравнение (его называют уравнением Шрёдингера в честь Шрёдингера, который его и открыл).
Закон движения экземпляров в пространстве: Пусть —
квантовое состояние частицы, вектор-столбец, в котором одна за другой записаны амплитуды во всех клетках пространства.
— оператор энергии, определяющий способ взаимодействия между экземплярами. Тогда рой движется согласно следующему закону:
.
Формирование оператора энергии «по кусочкам ручками» будет рассмотрено в следующей статье.
Квантовая система
| Основа |
|---|
| Классическая механика · Интерференция · Бра и кет · Гамильтониан |
| Фундаментальные понятия |
|---|
| Квантовое состояние · Волновая функция · Суперпозиция · Запутанность · |
| Эксперименты |
|---|
| Опыт Дэвиссона — Джермера · Опыт Поппера · Опыт Штерна — Герлаха · Опыт Юнга ·Проверка неравенств Белла · Фотоэффект · Эффект Комптона |
| Формулировки |
|---|
| Картина Шрёдингера · Картина Гейзенберга · Картина взаимодействия · Матричная квантовая механика · Интегралы по траекториям |
| Уравнения |
|---|
| Уравнение Шрёдингера · Уравнение Паули · Уравнение Клейна — Гордона · Уравнение Дирака |
| Интерпретации |
|---|
| Копенгагенская интерпретация · Теория скрытых параметров · Многомировая |
| Сложные темы |
|---|
| Квантовая теория поля · Квантовая гравитация · Теория всего |
| Известные учёные |
|---|
| Планк · Эйнштейн · Шрёдингер · Гейзенберг· Йордан · Бор · Паули · Дирак · Фок · Борн · де Бройль · Ландау · Фейнман · Бом · Эверетт |
Ква́нтовая меха́ника (другие названия: волновая механика, матричная механика) — раздел теоретической физики, описывающий квантовые системы и законы их движения.
Основными понятиями квантовой кинематики являются понятия наблюдаемой, состояния, среднего значения.
Содержание
История
На заседании Немецкого физического общества Макс Планк зачитал свою историческую статью «К теории распределения энергии излучения в нормальном спектре», в которой он ввел универсальную постоянную h. Именно дату этого события, 14 декабря 1900 года, часто считают днем рождения квантовой теории.
Квантовая гипотеза Макса Планка состояла в том, что любая энергия поглощается или испускается только дискретными порциями, которые состоят из целого числа квантов с энергией ε таких, что эта энергия пропорциональна частоте ν с коэффициентом пропорциональности, определённым по формуле:
В 1905 году для объяснения явлений фотоэффекта Альберт Эйнштейн, использовав квантовую гипотезу Планка, предположил, что свет состоит из квантов, которые впоследствии назвали фотонами.
Для объяснения структуры атома Нильс Бор в 1913 году предложил существование стационарных состояний электрона, в которых энергия может принимать лишь дискретные значения. Этот подход, развитый Арнольдом Зоммерфельдом и другими физиками, часто называют старой квантовой теорией (1900—1924). Отличительной чертой старой квантовой теории, является сочетание классической теории и противоречащими ей дополнительными предположениями.
В 1925—1926 годах была заложены основы последовательной квантовой теории, в виде квантовой механики, содержащей новые фундаментальные законы кинематики и динамики. Первая формулировка квантовой механики содержится в статье Вернера Гейзенберга, датированная 29 июля 1925 года. Эту дату можно считать днем рождения нерелятивистской квантовой механики. Отметим, что развитие и формирование основ квантовой механики продолжается до сих пор, и связано, например, с исследованиями открытых и диссипативных квантовых систем, квантовой информатикой, квантовым хаосом и др. Помимо квантовой механики, важнейшей частью квантовой теории является квантовая теория поля.
Математические основания квантовой механики
Математический аппарат нерелятивистской квантовой механики строится на следующих положениях: [1]
Эти положения позволяют создать математический аппарат, пригодный для описания широкого спектра задач в квантовой механике гамильтоновых систем, находящихся в чистых состояниях. Дальнейшим развитием этого аппарата является уравнение Дирака, которое с хорошей точностью позволяет описать релятивистские эффекты. Для динамики открытых, негамильтоновых и диссипативных квантовых систем применяется уравнение Линдблада.
Необычные явления, мысленные эксперименты и парадоксы квантовой механики
Разделы квантовой механики
В стандартных курсах квантовой механики изучаются следующие разделы
Комментарии
См. также
Литература
Примечания
Ссылки
| Разделы механики | п · о · р | |
|---|---|---|
| теоретическая механика | небесная механика | квантовая механика | классическая механика | сопротивление материалов | строительная механика | теория колебаний | теория упругости | теория пластичности | теория устойчивости | теория катастроф|> | ||
Полезное
Смотреть что такое «Квантовая система» в других словарях:
квантовая система — Отдельные частицы вещества или совокупности частиц, процессы в которых подчиняются законам квантовой механики. [ГОСТ 15093 90] Тематики лазерное оборудование … Справочник технического переводчика
квантовая система — kvantinė sistema statusas T sritis fizika atitikmenys: angl. quantum system vok. Quantensystem, n rus. квантовая система, f pranc. système quantique, m … Fizikos terminų žodynas
Квантовая механика — Квантовая механика … Википедия
Квантовая телепортация — Квантовая телепортация передача квантового состояния на расстояние при помощи разъединённой в пространстве сцепленной(запутанной) пары и классического канала связи, при которой состояние разрушается в точке отправления при проведении… … Википедия
Квантовая теория открытых систем — Открытая система в квантовой механике квантовая система, которая может обмениваться энергией и веществом с внешней средой. В определенном смысле всякая квантовая система может рассматриваться как открытая система, поскольку измерение любой… … Википедия
КВАНТОВАЯ МЕХАНИКА — (волновая механика), теория, устанавливающая способ описания и законы движения микрочастиц (элем. ч ц, атомов, молекул, ат. ядер) и их систем (напр., кристаллов), а также связь величин, характеризующих ч цы и системы, с физ. величинами,… … Физическая энциклопедия
Квантовая теория поля — Квантовая теория поля квантовая теория систем с бесконечным числом степеней свободы (полей физических (См. Поля физические)). К. т. п., возникшая как обобщение квантовой механики (См. Квантовая механика) в связи с проблемой описания… … Большая советская энциклопедия
КВАНТОВАЯ ТЕОРИЯ ПОЛЯ — (КТП), релятивистская квант. теория физ. систем с бесконечным числом степеней свободы. Пример такой системы эл. магн. поле, для полного описания к рого в любой момент времени требуется задание напряжённостей электрич. и магн. полей в каждой точке … Физическая энциклопедия
Квантовая криптография — Квантовая криптография метод защиты коммуникаций, основанный на принципах квантовой физики. В отличие от традиционной криптографии, которая использует математические методы, чтобы обеспечить секретность информации, квантовая криптография… … Википедия