что такое исключающее или в логике
Практика применения XOR в программировании
В данной статье я расскажу о битовой операции XOR (исключающее ИЛИ) и приведу наиболее интересные примеры ее применения на JAVA.
Итак, XOR – операция, которая принимает значение «истина» только если всего один из аргументов имеет значение «истина».
XOR обладает следующими свойствами:
a XOR 0 = a
a XOR a = 0
a XOR b = b XOR a
(a XOR b) XOR b = a
В языке JAVA (а также в С, С++, C#, Ruby, PHP, JavaScript) операция обозначается символом «^».
Обмен значений переменных без использования дополнительной переменной
С использованием операции XOR можно реализовать обмен значений однотипных пременных без использования дополнительной переменной:
или в более короткой записи:
Таким образом можно, например, реализовать реверс текстовой строки:
Следует, однако, заметить, что такой код не дает выигрыша в скорости по сравнению с кодом использующим временную переменную.
Шифрование
Шифрование на основе операций XOR использует свойство:
(a XOR k) XOR k = a
где k – выступает в роли ключа
Простая реализация шифрования строки:
Попробуем зашифровать строку “Съешь ещё этих мягких французских булок, да выпей чаю.” И в качестве ключа возьмем слово “хабра”:
Узким местом такого шифрования является то, что зная часть зашифрованного текста можно с легкостью восстановить ключ и, соответственно, расшифровать весь текст. Поэтому в чистом виде он редко используется на практике, хотя его применяют как часть более сложных алгоритмов шифрования.
Интересно, что в свое время данный алгоритм использовался Microsoft для шифрования содержимого документов в Office 95.
Генератор случайных чисел XORShift
В 2003 году Джордж Марсаглия представил миру быстрый алгоритм генерации случайных чисел с использованием XOR – XORShift.
Одна из возможных его рализаций:
39462749392662495
4596835458788324745
-7932128052244037525
-2502212788642280052
3288035714308340525
-8561046377475020727
-812160615072319265
-3869866974339671508
-7329504029400927428
3890915262874757420
В заключение просьба тем, у кого есть другие красивые примеры применения XOR, не вошедшие в статью, рассказать о них.
Трюк с XOR для собеседований и не только
Есть целая куча популярных задач для собеседований, которые можно решить одним из двух способов: или логичным применением стандартных структур данных и алгоритмов, или использованием некоторых свойств XOR сложным для понимания способом.
Хоть и непривычно ожидать решения с XOR на собеседованиях, довольно забавно разбираться, как они работают. Оказывается, все они основаны на одном фундаментальном трюке, который я постепенно раскрою в этом посте. Далее мы рассмотрим множество способов применения этого трюка с XOR, например, при решении популярной задачи с собеседований:
Дан массив из n — 1 целых чисел, находящихся в интервале от 1 до n. Все числа встречаются только один раз, за исключением одного числа, которого нет. Найдите отсутствующее число.
В большинстве языков программирования ^ реализован как побитовый оператор, то есть XOR по отдельности применяется к каждому биту в строке битов (например, в байте).
Благодаря этому мы можем применять XOR к чему угодно, а не только к булевым значениям.
Выявляем полезные свойства
Из представленного выше определения можно вывести несколько свойств. Давайте разберём их по порядку, а затем скомбинируем их для решения задач с собеседований.
XOR и 0: x ^ 0 = x
| x | y | x ^ y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
XOR с одинаковыми аргументами: x ^ x = 0
| x | y | x ^ y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Это означает, что применив XOR к одинаковым аргументам, мы их взаимно уничтожим.
Коммутативность: x ^ y = y ^ x
Операция XOR коммутативна, то есть мы можем менять порядок применения XOR. Чтобы доказать это, можно взглянуть на таблицу истинности x ^ y и y ^ x :
Как мы видим, x ^ y и y ^ x всегда дают одинаковые значения.
Последовательности операций XOR
Скомбинировав всё это, мы можем вывести главную мысль, стоящую в основе всего дальнейшего:
Давайте разберём пример:
Способ применения 1: перемена значений местами
Прежде чем приступать к задаче поиска отсутствующего числа, давайте начнём с более простой задачи:
Поменяйте местами два значения x и y без использования вспомогательных переменных.
Оказывается, эту задачу можно легко решить при помощи трёх команд XOR:
Это кажется довольно загадочным. Почему при этом x и y поменяются местами?
Чтобы понять, как это происходит, давайте разберёмся пошагово. В комментарии после каждой команды указаны текущие значения (x, y) :
Воспользовавшись выведенными ранее свойствами, мы видим, что это на самом деле так.
Способ применения 2: поиск отсутствующего числа
Давайте наконец решим задачу, представленную в начале поста:
Дан массив A из n — 1 целых чисел, находящихся в интервале от 1 до n. Все числа встречаются в нём ровно один раз, за исключением одного отсутствующего числа. Найти это отсутствующее число.
Разумеется, есть множество прямолинейных решений этой задачи, но мы решили использовать XOR.
Из трюка с XOR мы знаем, что имея последовательность операторов XOR, можно убрать из неё все повторяющиеся аргументы. Однако если мы просто применим XOR ко всем значениям массива, то не сможем воспользоваться этим трюком, потому что в нём нет одинаковых значений:
Так мы получим последовательность операторов XOR, в которой элементы встречаются следующим образом:
В коде это будет выглядеть примерно так:
С первого взгляда на код алгоритм понять сложно. Однако если знать, как работает трюк с XOR, то он становится довольно тривиальным. По-моему, именно поэтому не стоит ждать такого решения на собеседованиях: оно требует знания очень специфичного трюка, но почти никакого алгоритмического мышления.
Прежде чем мы перейдём к следующему способу применения, я сделаю пару замечаний.
Использование этого трюка не только для целых чисел
Хоть мы пока работали только с целыми числами от 1 до n, это необязательно. На самом деле, предыдущий алгоритм работает в любой ситуации, где есть (1) некоторое множество потенциальных элементов и (2) множество действительно встречающихся элементов. Эти множества могут отличаться только одним отсутствующим элементом. Это замечательно сработало для целых чисел, потому что множество потенциальных элементов соответствует элементам от 1 до n.
Можно придумать способы применения, где элементы не являются целыми числами от 1 до n:
Арифметические операции вместо XOR
Если алгоритм по-прежнему кажется вам непостижимым и магическим (надеюсь, это не так), то может быть полезным подумать, как достичь того же результата при помощи арифметических операторов. На самом деле всё довольно просто:
Способ применения 3: поиск повторяющегося числа
И вот здесь всё становится интереснее: мы можем применить точно такое же решение к похожей задаче с собеседования:
Дан массив A из n + 1 целых чисел, находящихся в интервале от 1 до n. Все числа встречаются ровно один раз, за исключением одного числа, которое повторяется. Найти это повторяющееся число.
Давайте подумаем, что произойдёт, если мы просто применим алгоритм из предыдущего решения. Мы получим последовательность операторов XOR, в которой элементы встречаются следующим образом:
Все остальные элементы взаимно уничтожаются, потому что встречаются ровно два раза.
Способ применения 4: поиск двух отсутствующих/повторяющихся чисел
Оказывается, мы можем расширить возможности алгоритма. Рассмотрим чуть более сложную задачу:
Дан массив A из n — 2 целых чисел, находящихся в интервале от 1 до n. Все числа встречаются ровно один раз, за исключением двух отсутствующих чисел. Найти эти два отсутствующих числа.
Как и ранее, задача полностью эквивалентна поиску двух повторяющихся чисел.
Как вы наверно догадались, мы будем придерживаться того, что сработало раньше, и начнём точно так же: рассмотрим, что произойдёт, если использовать предыдущий алгоритм с XOR. Если мы его применим, то получим последовательность операторов XOR, в которой все элементы взаимно уничтожают друг друга, за исключением тех, которые мы ищем.
Разделение при помощи изучения u ^ v
К счастью, мы можем понять, что делать, воспользовавшись изложенным выше. Давайте подумаем:
Упрощаем задачу
Далее мы можем использовать ещё одно сделанное ранее открытие:
Хоть пока мы работали только с целыми числами от 1 до n, это необязательно. На самом деле, предыдущий алгоритм работает в любой ситуации, где есть (1) некоторое множество потенциальных элементов и (2) множество действительно встречающихся элементов. Эти множества могут отличаться только одним отсутствующим (или повторяющимся) элементом.
На самом деле это очень удобный способ решения задачи: по сути, мы сводим данную новую задачу к более общей версии решённой ранее задачи.
Достигнуть предела
Следовательно, задача требует более сложных решений, больше не использующих XOR.
Заключительные мысли
Как говорилось выше, наверно, не стоит давать такие задачи на собеседованиях. Для их решения нужно знать не сразу понятный трюк, но если он известен, то решать больше практически нечего (возможно, за исключением способа применения 4). Едва ли таким образом кандидат продемонстрирует алгоритмическое мышление (кроме навыков упрощения) и здесь не особо получится использовать структуры данных.
Однако здорово было выяснить, как этот трюк работает. Похоже, XOR обладает идеально подходящими для этой задачи свойствами. Кроме того, есть некая красота в том, что нечто столь фундаментальное, как XOR, можно использовать для создания описанных в статье алгоритмов.
На правах рекламы
VDSina предлагает виртуальные серверы на Linux и Windows — выбирайте одну из предустановленных ОС, либо устанавливайте из своего образа.
Основные логические операции. AND, NOT, OR и XOR (исключающее или)
В этой статье мы поговорим о некоторых битовых операциях. Рассмотрим основные из них: XOR (исключающее ИЛИ), AND (И), NOT (НЕ) а также OR (ИЛИ).
Как известно, минимальной единицей измерения информации является бит, который хранит одно из 2-х значений: 0 (False, ложь) либо 1 (True, истина). Таким образом, битовая ячейка может одновременно находиться лишь в одном из двух возможных состояний.
Для манипуляций с битами используют определённые операции — логические или булевые. Они могут применяться к любому биту, вне зависимости от того, какое у него значение — ноль или единица. Что же, давайте посмотрим на примеры использования трёх основных логических операций.
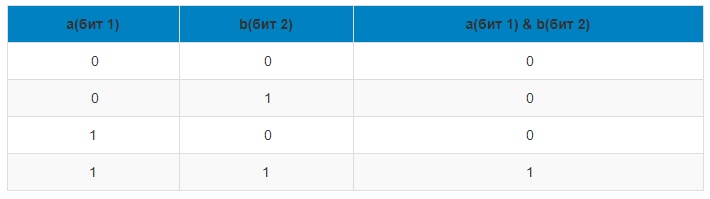
Логическая операция AND (и)
Оператор AND выполняется с 2-мя битами, возьмём, к примеру, a и b. Результат выполнения операции AND равен 1, если a и b равняются 1. В остальных случаях результат равен 0. Например, с помощью AND вы можете узнать, чётное число или нет.
Посмотрите на таблицу истинности операции AND:
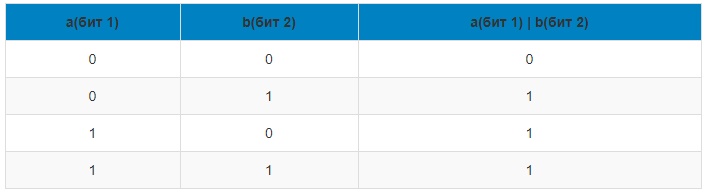
Логическая операция OR (ИЛИ)
Оператор OR также выполняется с 2-мя битами (a и b). Результат равен 0, если a и b равны 0, иначе он равен 1. Смотрим таблицу истинности.
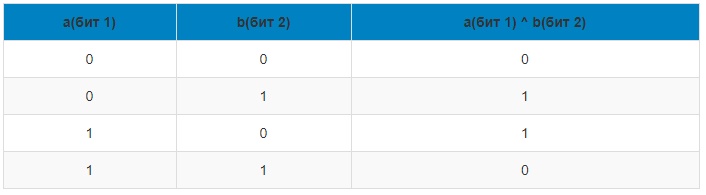
Логическая операция XOR (исключающее ИЛИ)
XOR выполняется с 2-мя битами (a и b). Результат выполнения операции XOR (исключающее ИЛИ) равен 1, когда один из битов b или a равен 1. В остальных ситуациях результат применения оператора XOR равен 0.
Таблица истинности логической операции для XOR (исключающее ИЛИ) выглядит так:
Используя XOR (исключающее ИЛИ), вы можете поменять значения 2-х переменных одинакового типа данных, не используя временную переменную. А ещё, посредством XOR можно зашифровать текст, например:
Согласен, XOR — далеко не самый надёжный метод шифрования, но это не значит, что его нельзя сделать частью какого-либо шифровального алгоритма.
Логическая операция NOT (НЕ)
Это побитовое отрицание, поэтому выполняется с одним битом и обозначается
Результат зависит от состояния бита. Если он в нулевом состоянии, то итог операции — единица и наоборот. Всё предельно просто.
Эти 4 логические операции следует запомнить в первую очередь, т. к. с их помощью можно получить практически любой возможный результат. Также существуют такие операции, как (побитовый сдвиг влево) и >> (побитовый сдвиг вправо).
Что такое исключающее или в логике
Войти
Авторизуясь в LiveJournal с помощью стороннего сервиса вы принимаете условия Пользовательского соглашения LiveJournal
Проект «логика для чайников». Параграф 26.
Простейшие логические операции
Простейшие логические операции относятся к двузначной логике. Их 4 штуки: “НЕ”, “И”, “ИЛИ”, “XOR”. Также для обозначения этих операций используют разные значки (“
При записи логических формул вместо слов “истина” и “ложь” обычно используют стандартные международные обозначения:
Вместо “истина” пишут: true, T, t, 1.
Вместо “ложь” пишут: false, F, f, 0.
Операция “НЕ” преобразует истину в ложь, а ложь в истину:
НЕ true = false
НЕ false = true
У этой операции бывают разные другие названия: “логическое НЕ”, “отрицание”, “логическое отрицание”, “инверсия”, “логическая инверсия”. Для международных обозначений вместо “НЕ” пишут “NOT”.
В естественном языке этой операции соответствует добавление слов “неправда, что. ” в начале высказывания. Например:
“Сурков должен мне денег”. (1)
Применение операции “НЕ” к высказыванию (1):
“Неправда, что Сурков должен мне денег”. (2)
Если высказывание (1) ложно, то высказывание (2) истинно. Если высказывание (2) ложно, то высказывание (1) истинно.
Нетрудно понять, что двойное применение “НЕ” возвращает нас к прежней истинности.
“Неправда, что неправда, что Сурков должен мне денег”. (3)
Истинность высказывания (3) всегда совпадает с истинностью высказывания (1).
Операция “И” применяется к двум высказываниям. Ее результат “истина”, только если оба высказывания истинны (а иначе “ложь”):
false И false = false
false И true = false
true И false = false
true И true = true
У этой операции бывают разные другие названия: “логическое И”, “конъюнкция”, “логическое умножение”. Для международных обозначений вместо “И” пишут “AND”.
В естественном языке этой операции соответствует вставка союза “и” между высказываниями. Например:
“Сурков должен мне денег”. (1)
“Петров должен мне денег”. (2)
Применение операции “И” к высказываниям (1) и (2):
“Сурков должен мне денег, и Петров должен мне денег”. (3)
Эту фразу можно сократить, сохранив прежний смысл:
“Сурков и Петров должны мне денег”. (3)
Высказывание (3) истинно только тогда, когда истинны оба высказывания: (1) и (2). Если хотя бы одно из них ложно, то результат тоже ложен. Если оба ложны – тоже.
То есть, если Петров мне денег не задолжал, а задолжал только Сурков, тогда высказывание (3) не будет “полуправдой” или “полуложью”, а будет просто ложью.
Операция “ИЛИ” применяется к двум высказываниям. Ее результат “истина”, если хотя бы одно высказывание истинно (а иначе “ложь”):
false ИЛИ false = false
false ИЛИ true = true
true ИЛИ false = true
true ИЛИ true = true
У этой операции бывают разные другие названия: “логическое ИЛИ”, “включающее ИЛИ”, “дизъюнкция”, “логическое сложение”. Для международных обозначений вместо “ИЛИ” пишут “OR”.
В естественном языке этой операции соответствует вставка союза “или” между высказываниями, но. не всегда (см. ниже об операции “XOR”). Например:
“Я хочу попить”. (1)
“Я хочу поесть”. (2)
Применение операции “ИЛИ” к высказываниям (1) и (2):
“Я хочу попить, или я хочу поесть”. (3)
По-русски звучит правильно, но коряво, и эту фразу можно сократить, сохранив прежний смысл:
“Я хочу попить или поесть ”. (3)
Высказывание (3) истинно тогда, когда истинно хотя бы одно из высказываний (1) и (2), а можно оба. Если оба высказывания ложны, то результат тоже ложен.
То есть, если я хочу есть, но не пить, тогда высказывание (3) истинно. Если я не прочь и поесть, и попить, выказывание (3) тоже истинно. Ложно оно тогда, когдя я не хочу ни того, ни другого.
Операция “XOR” применяется к двум высказываниям. Ее результат “истина”, если ровно одно из высказываний истинно (а иначе “ложь”):
false XOR false = false
false XOR true = true
true XOR false = true
true XOR true = false
У этой операции бывают разные другие названия: “исключающее ИЛИ”, “сложение по модулю 2”, “логическое сложение по модулю 2”. “XOR” – это международное обозначение, общепринятого “русского” аналога нет.
В естественном языке этой операции соответствует вставка союза “или” между высказываниями – так же, как в случае с операцией “ИЛИ”. Например:
“Я собираюсь просить прибавки к зарплате”. (1)
“Я попытаюсь сэкономить ”. (2)
Применение операции “XOR” к высказываниям (1) и (2):
“Я собираюсь просить прибавки к зарплате или я попытаюсь сэкономить”. (3)
“Я собираюсь просить прибавки к зарплате или попытаюсь сэкономить”. (3)
Высказывание (3) истинно тогда, когда истинно ровно одно из высказываний (1) и (2). Если я не собираюсь ни просить прибавки, ни экономить, тогда фраза ложна. Также, я имел в виду, что не собираюсь делать и то, и другое одновременно.
Обратите внимание на разницу между операциями “ИЛИ” и “XOR”. Она заключается только в последнем правиле:
true ИЛИ true = true
true XOR true = false
В естественном языке обе операции изображаются одним и тем же союзом “или”. Это – пример неоднозначности естественного языка. Если помните, омонимы и многозначные слова могут иметь больше одного значения. Союз “или” именно такой: он имеет два возможных значения. Первое выражается логической операцией “ИЛИ”, второе – логической операцией “XOR”.
В английском языке существуют те же проблемы: союз “or” имеет те же два значения. А вот древним римлянам было проще, так как в латыни есть два разных слова: “vel” (операция “ИЛИ”) и “aut” (операция “XOR”).
Поскольку разница между операциями “ИЛИ” и “XOR” невелика (всего одно последнее правило), то иногда эта разница не имеет значения. Иногда о том, что имеется в виду, можно догадаться по интонации, или по контексту. Иногда определить точный смысл так и не удается.
ElectronicsBlog
Обучающие статьи по электронике
Логический элемент Исключающее ИЛИ
Всем доброго времени суток! Сегодня мы рассмотрим последние два элемента, которые выполняют простейшие логические функции. Такими элементами являются Исключающее ИЛИ (Exclusive-OR, XOR) и Исключающее ИЛИ-НЕ (None Exclusive-OR, NXOR). Предыдущие статьи смотрите здесь, здесь, здесь и здесь.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Логический элемент Исключающее ИЛИ, как и ранее рассмотренные логические элементы имеет несколько равноправных входов и один выход, но не один из входных выводов не может заблокировать другие входы, установив выходной сигнал к уровню единицы или нуля. Исходя из сказанного, можно установить логику работы элемента Исключающее ИЛИ: высокий логический уровень на выходе появляется только тогда, когда только на одном из входов есть высокий уровень, а если на всех входах одновременно присутствуют сигналы логического нуля или логической единицы, то на выходе буде низкий уровень напряжения. Так же как и все остальные логические элементы элемент Исключающее ИЛИ может иметь инверсию на выходе, такой элемент называют Исключающее ИЛИ-НЕ. Логика работы такого элемента следующая: высокий уровень на выходе логического элемента Исключающее ИЛИ-НЕ появиться только в том случае, когда на всех входах одновременно присутствует сигналы лог. 0 или лог. 1. Таким образом таблица истинности логических элементов Исключающее ИЛИ и Исключающее ИЛИ-НЕ будет иметь следующий вид:
| Входные выводы | Тип логического элемента | ||
| 1 | 2 | Исключающее ИЛИ | Исключающее ИЛИ-НЕ |
| 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Элементы Исключающее ИЛИ из-за своего специфического функционала не имеют широкого применения, поэтому отдельных суффиксов в их обозначении не присутствует, они в основном входят в серию ЛП (например, К555ЛП5, КР1533ЛП12, К561ЛП2), в составе которой микросхемы с различным функционалом. Логические элементы Исключающее ИЛИ имеют своё графическое обозначение, которое приведено ниже.
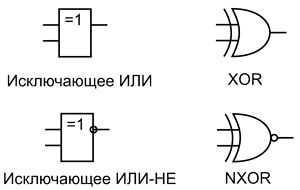
Условное графическое обозначение элементов Исключающее ИЛИ: DIN (слева) и ANSI (справа).
Применение элемента Исключающее ИЛИ
С точки зрения математики, элемент Исключающее ИЛИ выполняет операцию суммирования по модулю 2. Поэтому эти элементы иногда называют сумматорами по модулю два. Основное предназначение элементов Исключающее ИЛИ состоит в сравнении двух входных сигналов (когда на входы приходят два высоких или два низких логических уровня на выходе формируется лог. 0), очень часто данный элемент применяют для формирования задержки сигнала или формирования коротких импульсов.
Управляемый инвертор
Важное применение элементов Исключающее ИЛИ – управляемый инвертор. Опишем его работу. Один из входов используется как управляющий, а на другой поступает сигнал. Если на управляющем входе высокий логический уровень, то сигнал инвертируется, а если низкий, то не инвертируется. Чаще всего управляющий сигнал задаётся постоянным уровнем, определяя режим работы элемента, а информационный сигнал является импульсным. То есть элемент Исключающее ИЛИ может изменять полярность входного сигнала или фронта, а может и не изменять в зависимости от управляющего сигнала.
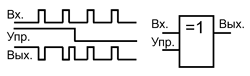
Элемент Исключающее ИЛИ в качестве управляемого инвертора.
Смешивание сигналов
В случае, когда имеется два сигнала и исключается их одновременный приход на элемент Исключающее ИЛИ, то он может быть использован для смешивания сигналов. Такое применение данного элемента может быть использовано в тех случаюх, когда остаются неиспользованными некоторые элементы Исключающее ИЛИ.
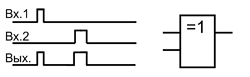
Применение элемента Исключающее ИЛИ для смешивания двух неодновременных сигналов.
Формирование коротких импульсов
Второе важное применение данного элемента – выделение фронта и среза входного импульса, которое традиционно делали с помощью дифференцирующего RC-звена, с последующим усилением и формированием сигнала. Микросхема с элементами Исключающее ИЛИ упрощает данную задачу.
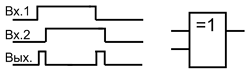
Выделения фронта и среза импульса.
Ниже представлена схема для выделения среза и фронта входящего импульса. Входной сигнал задерживается цепочкой элементов, а затем исходный сигнал и его задержаная копия поступают на входы элемента Исключающее ИЛИ. В результате такого преобразования можно говорить об удвоении частоты входного сигнала, так как выходные импульсы следуют вдвое чаще, чем входные.
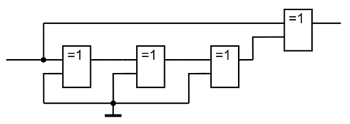
Схема реализующая выделение фронта и среза импульса.
Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.