что такое граф связей
Алгоритмы на графах — Часть 0: Базовые понятия
Как оказалось тема алгоритмов интересна Хабра-сообществу. Поэтому я как и обещал, начну серию обзоров «классических» алгоритмов на графах.
Так как публика на Хабре разная, а тема интересна многим, я должен начать с нулевой части. В этой части я расскажу что такое граф, как он представлен в компьютере и зачем он используется. Заранее прошу прощения у тех кто это все уже прекрасно знает, но для того чтобы объяснять алгоритмы на графах, нужно сначала объяснить что такое граф. Без этого никак.
В математике, Граф — это абстрактное представление множества объектов и связей между ними. Графом называют пару (V, E) где V это множество вершин, а E множество пар, каждая из которых представляет собой связь (эти пары называют рёбрами).
Граф может быть ориентированным или неориентированным. В ориентированном графе, связи являются направленными (то есть пары в E являются упорядоченными, например пары (a, b) и (b, a) это две разные связи). В свою очередь в неориентированном графе, связи ненаправленные, и поэтому если существует связь (a, b) то значит что существует связь (b, a).
Неориентированный граф: Соседство (в жизни). Если (1) сосед (3), то (3) сосед (1). См рис. 1.а
Ориентированный граф: Ссылки. Сайт (1) может ссылаться на сайт (3), но совсем не обязательно (хотя возможно) что сайт (3) ссылается сайт (1). См рис. 1.б
Путь в графе это конечная последовательность вершин, в которой каждые две вершины идущие подряд соединены ребром. Путь может быть ориентированным или неориентированным в зависимости от графа. На рис 1.а, путем является например последовательность [(1), (4), (5)] на рис 1.б, [(1), (3), (4), (5)].
У графов есть ещё много разных свойств (например они могут быть связными, двудольными, полными), но я не буду описывать все эти свойства сейчас, а в следующих частях когда эти понятия понадобятся нам.
Представление графов
Существует два способа представления графа, в виде списков смежности и в виде матрицы смежности. Оба способа подходят для представления ориентированных и неориентированных графов.
Матрица смежности
Этот способ является удобным для представления плотных графов, в которых количество рёбер (|E|) примерно равно количеству вершин в квадрате (|V| 2 ).
В данном представлении мы заполняем матрицу размером |V| x |V| следущим образом:
A[i][j] = 1 (Если существует ребро из i в j)
A[i][j] = 0 (Иначе)
Данный способ подходит для ориентированных и неориентированных графов. Для неориентированных графов матрица A является симметричной (то есть A[i][j] == A[j][i], т.к. если существует ребро между i и j, то оно является и ребром из i в j, и ребром из j в i). Благодаря этому свойству можно сократить почти в два раза использование памяти, храня элементы только в верхней части матрицы, над главной диагональю)
Понятно что с помощью данного способа представления, можно быстро проверить есть ли ребро между вершинами v и u, просто посмотрев в ячейку A[v][u].
С другой стороны этот способ очень громоздкий, так как требует O (|V| 2 ) памяти для хранения матрицы.

На рис. 2 приведены представления графов из рис. 1 с помощью матриц смежности.
Списки смежности
Данный способ представления больше подходит для разреженных графов, то есть графов у которых количество рёбер гораздо меньше чем количество вершин в квадрате (|E| 2 ).
В данном представлении используется массив Adj содержащий |V| списков. В каждом списке Adj[v] содержатся все вершины u, так что между v и u есть ребро. Память требуемая для представления равна O (|E| + |V|) что является лучшим показателем чем матрица смежности для разреженных графов.
Главный недостаток этого способа представления в том, что нет быстрого способа проверить существует ли ребро (u, v).

На рис. 3 приведены представления графов из рис. 1 с помощью списков смежности.
Применение
Те кто дочитал до этого места, наверное задали себе вопрос, а где же собственно я смогу применить графы. Как я и обещал я буду стараться приводить примеры. Самый первый пример который приходит в голову это социальная сеть. Вершинами графа являются люди, а ребрами отношения (дружба). Граф может быть неориентированным, то есть я могу дружить только с теми кто дружит со мной. Либо ориентированным (как например в ЖЖ), где можно добавить человека в друзья, без того чтобы он добавлял вас. Если же он да добавит вас вы будете «взаимными друзьями». То есть будет существовать два ребра: (Он, Вы) и (Вы, Он)
Ещё одно из применений графа, которое я уже упоминал это ссылки с сайта на сайт. Представим Вы хотите сделать поисковую систему и хотите учесть на какие сайты есть больше ссылок (например сайт A), при этом учитывать сколько сайтов ссылается на сайт B, который ссылается на сайт A. У вас будет матрица смежности этих ссылок. Вы захотите ввести какую то систему подсчёта рейтинга, которая делает какие то подсчёты на этой матрице, ну, а дальше… это Google (точнее PageRank) =)
Заключение
Это небольшая часть теории которая понадобится нам чтобы для следующих частей. Надеюсь вам было понятно, а главное понравилось и заинтересовало читать дальнейшие части! Оставляйте свои отзывы и пожелания в комментариях.
В следующей части
BFS — Алгоритм поиска в ширину
Библиография
Кормен, Лайзерсон, Риверст, Штайн — Алгоритмы. Построение и анализ. Издательство Вильямс, 2007.
Словарь терминов теории графов
Граф — статья в английской Википедии
Статья это кросс-пост из моего блога — «Programing as is — записки программиста»
Метод графов связей. Построение графов связей для систем различной физической природы. Причинность. Эквивалентные преобразования графов связей.
Метод графов связей, или связных графов основан на представлении о том, что любые физические процессы состоят из элементарных актов преобразования энергии. Такими элементарными процессами являются накопление энергии, диссипация (потери) энергии и преобразование энергии без потерь.
Граф связей представляет собой совокупность элементов, соответствующих основным типам преобразования энергии и изображаемых в качестве вершин графа, соединенных связями (дугами графа). Основные переменные связей – усилие e(t) и поток f (t).
Интерпретация переменных связи для объектов различной физической природы представлена в таблице:
Физическая интерпретация для элементов (узлов) графа представлена в таблице:
Причинная стрелка является указателем направления усилия и потока.
Перечисленные правила позволяют расставить причинные отношения в любом графе связей, причем, как правило, несколькими способами. Можно рекомендовать следующую последовательность выполнения этой процедуры.
1. В первую очередь расставляются причинные отношения на связях источников энергии, поскольку они предопределены типами источников и не допускают свободы выбора.
2. Затем задаются причинности на связях аккумуляторов. Можно рекомендовать для всех аккумуляторов выбирать один тип причинности, например интегральный.
3. Последовательно, в соответствии с правилами, расставляются причинные отношения на остальных связях графа. Если на этом этапе появляется причинное противоречие, то можно вернуться к предыдущему пункту и изменить направление причинности у одного или нескольких аккумуляторов.
Заметка: 0 узел может иметь сколь угодно много причинностей, но при этом только одна причинность не должна быть направлена к нему. 1 узел – напротив только одну причинность, остальные от него.
Таблица упрощений (левая колонка исходный граф – правая его упрощение)
Графы связей и структурные схемы. Методы построения структурных схем и расчета передаточных функций с использованием методологии графов связей.
Построение операторно-структурных схем основано на том, что явные зависимости потоков и усилий для элементов графа связей, получаемые после расстановки отношений причинности, могут быть, в случае линейных систем, отображены в виде функциональных направленных звеньев с соответствующими передаточными функциями. Проведем соответствия между элементами графа и ОСС в таблице на след странице.
Знаки слагаемых зависят от направления полустрелок на связях. Если направление связи слагаемого совпадает с направлением связи суммы, то слагаемое входит в сумму со знаком «+», в противном случае – со знаком «-».
Возможность получения различных вариантов операторноструктурных схем является одним из достоинств графа связей. Так можно расставив причинности по разному (интегральные и дифференциальный) получим разные операторно-структурные схемы, но с одинаковой общей передаточной функцией.
Дата добавления: 2019-07-17 ; просмотров: 595 ; Мы поможем в написании вашей работы!
7.3. Диаграмма связей (граф связей).
Диаграмма связей является главным образом логическим инструментом, противопоставленным диаграмме сродства, которая сама по себе была творческая. Примеры ситуаций, когда диаграмма связей может быть полезной:
Когда тема (предмет) настолько сложна, что связи между различными идеями не могут быть установлены при помощи обычного обсуждения.
Когда временная последовательность, согласно которой делаются шаги, является решающей.
Когда подозревается, что проблема, затронутая в вопросе, является исключительным симптомом более фундаментальной незатронутой проблемы.
Применяется два типа диаграммы связей:
Качественный граф связей;
Количественный граф связей.
В качественный граф связей нужно включать как проблемы, так и их причины разных уровней (рис.7.2.).
Для построения диаграммы связей этого типа выполняются следующие действия:
1. Выделите все факторы, которые могут иметь отношение к рассматриваемой проблеме. Для этого можно воспользоваться ранее разработанными диаграммами сродства и Исикавы.
2. Изобразите все возможные проблемы и причины с помощью прямоугольников.
Основная
Рис.7.2. Принципы построения диаграммы связей (качественный граф связей).
3. Идентифицируйте все возможные мыслимые причинные взаимосвязи между каждым фактором и другими и покажите их стрелками на этом графе.
4. Классифицируйте факторы в зависимости от роли, которую они играют в причинно-следственной ситуации.
5. Сконцентрируйте ваши усилия по совершенствованию на устранение основных причин рассматриваемой проблемы.
В отличии от качественного графа, оценивающего зависимости между факторами, иногда проще количественный подход к определению роли различных факторов. Общий вид количественного графа связей дан на рис.7.3.
Для построения диаграммы связей в виде количественного графа выполняются следующие действия:
1. Разместите обозначения рассматриваемых факторов произвольным образом на листе бумаги, желательно, примерно, по кругу.
0 Входит4 Выходит

2 Входят 0 выходит 1 входит3 выходят

2 Входят0 Выходит 2 входят0 выходит
Рис. 7.3. Принцип построения диаграммы связей (количественный граф связей)
2. Для каждого фактора оцените: на какие факторы он влияет, под влиянием каких факторов он находится сам. Это влияние отметьте стрелками. Направление стрелки будет указывать направление влияния.
3. После оценки всех взаимосвязей нужно подсчитать и отметить на диаграмме число стрелок, приходящих к каждому фактору и уходящих от него (например, «3 стрелки входят, 2 выходят»).
В зависимости от числа стрелок в каждом направлении для каждого фактора можно определить одну из двух ролей:
Генератор показателей или причина. Это фактор, имеющий много стрелок, влияющих на уровень показателей других факторов (имеет больше выходящих стрелок, чем входящих).
Индикатор результата или эффект. Это фактор, который указывает нечто, как результат действия генератора показателей (имеет больше входящих стрелок, чем выходящих).
Когда предпринимается попытка отыскать основную причину проблемы или эффект, то генератор показателей следует выбирать в качестве отправной точки для проведения исследований. Эти факторы – движущая сила процесса и они создают уровень его показателей.
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.
8.5. Граф связей
Граф связей предназначен для идентификации логических причинно-следственных связей в комплексе в какой-либо особо сложной, критической ситуации. С помощью графа можно визуализировать эти связи.
В граф рассматриваемого типа нужно включать как проблемы, так и их причины разных уровней. Эго показано на рис. 8.14. Данная диаграмма очень похожа на традиционную диаграмму причин и результатов. Однако Ролстадос в книге [2] показал, что она больше подходит для решения сложных проблем.
Рис. 8.4. Принципы построения графа связей
Качественный граф можно построить с помощью компьютера. Рекомендуемая программа называется FPT for Windows. Она помогает пользователю строить различные схемы и диаграммы.
Компания потратила много времени и денег на внедрение системы измерения показателей. Однако эта система так и не нашла широкого применения в компании. Сотрудники компании не любили работать с ней, а в некоторых случаях просто ее саботировали.
Рис. 8.15. Качественный граф связей для плохо работающей системы измерения
Количественный граф связей
Этот вариант графа изначально возник в связи с развитием бенчмаркинга, который описан далее в главе 10. Он предназначен, в частности, для определения и оценки того, как многие показатели влияют друг на друга. Описание количественного графа дано Б. Андерсеном и П. Петтерсеном в книге [1]. Количественные графы связей можно, однако, использовать и для более общих целей, чем просто классификация показателей. В отличие от качественного графа, оценивающего зависимости между факторами, иногда проще количественный подход к определению роли различных факторов.
Общий вид количественного графа дан на рис. 8.16.
О входит, 4 выходят
. После оценки всех взаимосвязей нужно подсчитать и отметить на диаграмме число стрелок, приходящих к каждому фактору я уходящих от него (например, «3 стрелки входят, 2 выходят»),
В зависимости от числа стрелок в каждом направлении для каждого фактора можно определить одну из двух ролей: Генератор показателей или причина.
Когда предпринимается попытка отыскать основную причину проблемы или эффект, то генератор показателей следует выбирать в качестве отправной точки для проведения исследования. Эти факторы — движущая сила процесса и они создают уровень его показателей.
Далее на рис. 8.17 приводится соответствующий количественный граф связей для предыдущего примера. Граф содержит ту же самую информацию, т.е. главная проблема заключается в том, что не работает.
Измерительная система [7 входит, 0 выходит], причем главный генератор показателей — плохо определенная мера [0 входит, 5 выходит] и нет обучения измерениям [0 входит, 3 выходит].
Рис. 8.17. Количественный граф связей для примера
ДИАГРАММА СВЯЗЕЙ (ГРАФ СВЯЗЕЙ)



Общий
заголовок для А и В
 |  |
 |  |
Общий заголовок А Общий заголовок В
для (а) и (в) для (с) и (д)
 |  |  |  |
 |  |  |  |
Устные Устные Устные Устные
данные(а) данные(в) данные (с) данные(д)
Рис.7.1. Принцип построения диаграммы сродства.
Работа заканчивается, когда все данные будут приведены в порядок, то есть, собраны в предварительные группы сродственных данных, когда вышеупомянутые конфликты будут разрешены. Оставшиеся конфликты будут разрешены во время дискуссии. Анализ заканчивается, когда сгруппируют данные в соответствии с подходящим количеством ведущих направлений.
Диаграмма связей является главным образом логическим инструментом, противопоставленным диаграмме сродства, которая сама по себе была творческая. Примеры ситуаций, когда диаграмма связей может быть полезной:
· Когда тема (предмет) настолько сложна, что связи между различными идеями не могут быть установлены при помощи обычного обсуждения.
· Когда временная последовательность, согласно которой делаются шаги, является решающей.
· Когда подозревается, что проблема, затронутая в вопросе, является исключительным симптомом более фундаментальной незатронутой проблемы.
Применяется два типа диаграммы связей:
· Качественный граф связей;
· Количественный граф связей.
В качественный граф связей нужно включать как проблемы, так и их причины разных уровней (рис.7.2.).
Для построения диаграммы связей этого типа выполняются следующие действия:
1. Выделите все факторы, которые могут иметь отношение к рассматриваемой проблеме. Для этого можно воспользоваться ранее разработанными диаграммами сродства и Исикавы.
2. Изобразите все возможные проблемы и причины с помощью прямоугольников.
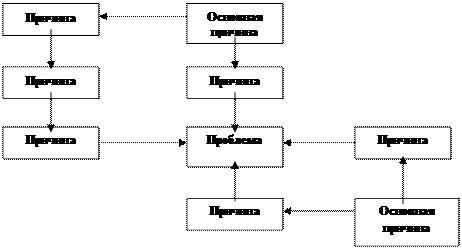 |
Рис.7.2. Принципы построения диаграммы связей (качественный граф связей).
3. Идентифицируйте все возможные мыслимые причинные взаимосвязи между каждым фактором и другими и покажите их стрелками на этом графе.
4. Классифицируйте факторы в зависимости от роли, которую они играют в причинно-следственной ситуации.
5. Сконцентрируйте ваши усилия по совершенствованию на устранение основных причин рассматриваемой проблемы.
В отличии от качественного графа, оценивающего зависимости между факторами, иногда проще количественный подход к определению роли различных факторов. Общий вид количественного графа связей дан на рис.7.3.
Для построения диаграммы связей в виде количественного графа выполняются следующие действия:
1. Разместите обозначения рассматриваемых факторов произвольным образом на листе бумаги, желательно, примерно, по кругу.
| |
 | |
 |

|
| ||
 |

|
|
Рис. 7.3. Принцип построения диаграммы связей (количественный граф связей)
2. Для каждого фактора оцените: на какие факторы он влияет, под влиянием каких факторов он находится сам. Это влияние отметьте стрелками. Направление стрелки будет указывать направление влияния.
3. После оценки всех взаимосвязей нужно подсчитать и отметить на диаграмме число стрелок, приходящих к каждому фактору и уходящих от него (например, «3 стрелки входят, 2 выходят»).
В зависимости от числа стрелок в каждом направлении для каждого фактора можно определить одну из двух ролей:
· Генератор показателей или причина.Это фактор, имеющий много стрелок, влияющих на уровень показателей других факторов (имеет больше выходящих стрелок, чем входящих).
· Индикатор результата или эффект.Это фактор, который указывает нечто, как результат действия генератора показателей (имеет больше входящих стрелок, чем выходящих).
Когда предпринимается попытка отыскать основную причину проблемы или эффект, то генератор показателей следует выбирать в качестве отправной точки для проведения исследований. Эти факторы – движущая сила процесса и они создают уровень его показателей.