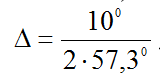что такое дсо и ддо

Диаграмма остойчивости и диаграмма динамической остойчивости (ДДО)

При статическом приложении кренящего момента восстанавливающий момент постепенно увеличивается вместе с нарастанием угла крена, и эти моменты взаимно уравновешивают друг друга в течение всего процесса статического накренения судна. Движение судна происходит равномерно, без угловых ускорений. Предположим теперь, что к судну, находящемуся в прямом положении, внезапно приложен кренящий момент, величина которого не связана с углом наклонения. Тогда график его действия можно изобразить на диаграмме статической остойчивости прямой линией ЕК параллельно оси (так действует, например, на судно внезапно налетевший порыв ветра (шквал), обрыв тяжелого груза, подвешенного на шкентеле вываленной за борт грузовой стрелы, обрыв буксирного троса). Под действием этого момента судно быстро накреняется.

Рис. 1

Рис. 2

Отсюда получаем правило, которое используется для графического решения уравнения (1): при заданном динамическом кренящем моменте М_КР положение ординаты Вθ_дин подбирают таким образом, чтобы заштрихованные площади оказались равными. Тогда пересечение с осью ординаты Вθ_дин даст искомый угол динамического крена. Определить динамический угол крена по диаграмме статической остойчивости можно лишь приближенно. Задачи, связанные с динамической остойчивостью, решаются быстрее и точнее с помощью так называемой диаграммы динамической остойчивости, которая представляет собой кривую, выражающую зависимость работы восстанавливающего момента от угла крена.

Построение такой диаграммы, являющейся интегральной кривой по отношению к диаграмме статической остойчивости, производится следующим образом. На оси абсцисс намечают несколько точек, соответствующих выбранным углам крена, и восстанавливают перпендикуляр до пересечения с кривой диаграммы статической остойчивости. Вычислив работу восстанавливающего момента (выраженную графически соответствующими площадями) при накренении судна от прямого положения ( θ = 0 ) до заданного угла крена, на перпендикулярах откладывают ординаты, которые в заданном масштабе определяют вычисленные значения площадей. Точки ординат соединяют плавной кривой, которая является диаграммой динамической остойчивости при данном состоянии нагрузки судна. На практике диаграмму динамической остойчивости строят по рассчитанным плечам динамической остойчивости методом определения интегральных сумм плеч статической остойчивости и расчета на основании этих сумм плеч динамической остойчивости.

Рис. 3

Определение минимального опрокидывающего момента по диаграмме статистической и динамической остойчивости

Предельные наклонения судна с помощью диаграмм статической и динамической остойчивости можно изобразить следующим образом:

Рис. 4

Мы видим, что предельный кренящий момент, действующий статически, всегда больше предельного кренящего момента, действующего динамически. Таким образом, для судна быстрое нарастание кренящего момента всегда более опасно, чем медленное.

Рассматривая вопросы, связанные с действием внезапно приложенного кренящего момента, мы исходим из предположения, что начальному положению судна соответствует угол крена, равный нулю (прямое положение). Между тем в практике эксплуатации судов бывают случаи, когда к началу действия внезапного кренящего момента судно уже находится в накрененном положении в результате действия какого-то кренящего момента. В этой ситуации при решении задач динамической остойчивости возможны два случая:

Рис. 5

По диаграмме динамической остойчивости значения опрокидывающего момента и вызываемого им крена определяют следующим образом:

Рис. 6

Нашли опечатку? Выделите и нажмите CTRL+Enter

Источник

Построение диаграмм статической и динамической остойчивости. Связь ддо и дсо. Задачи, решаемые с помощью диаграмм остойчивости.

Построение диаграммы статической остойчивости.

Статическая остойчивость – остойчивость, при которой кренящий момент приложенный к судну, нарастает постепенно от нуля до бесконечного значения и не вызывает угловых ускорений, а следовательно и сил инерции.

Диаграмма динамической остойчивости

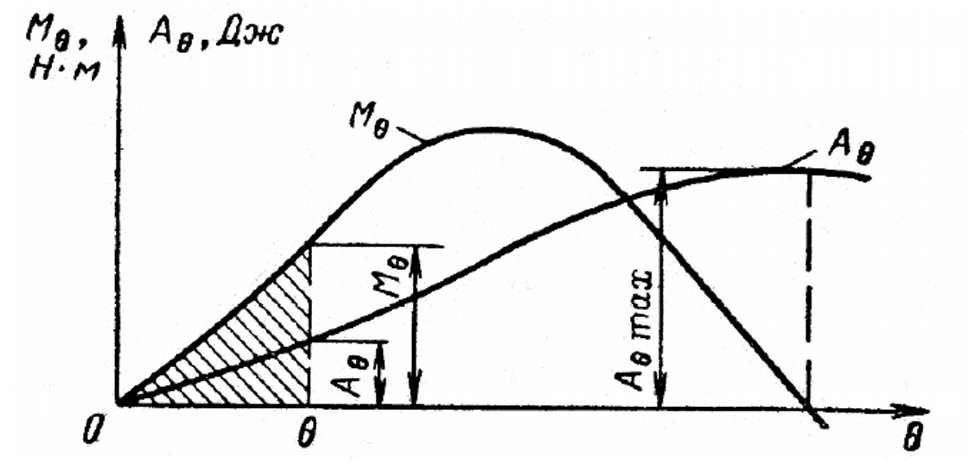
На ней можно отметить три точки, характерные для непов­режденного судна, обладающего положительной остойчивостью: точку О (начало координат), определяющую положение ус­тойчивою равновесия; точку А, где плечо статической остойчивости и восстанавливающий момент имеют максимальные значения; точку В, определяющую так называемый угол заката диаграммы.

Равновесие накренившегося судна наступает при равенстве кренящего и восстанавливающего моментов. Чтобы воспользоваться диаграммой статичес­кой остойчивости для определения угла крена, возникающего под действием заданного кренящего момента М_кр, необходимо найти плечо кренящего мо­мента . Условие равновесия судна можно написать и в таком виде: . Плечо откладывают в соответствующем масш­табе на оси ординат диаграммы и проводят горизонтальную линию до пере­сечения с кривой. В точке пересечения восстанавливающий момент равен кре­нящему, и, следовательно, судно находится в равновесии в наклоненном по­ложении. Точка пересечения перпендикуляра, опущенного из точки С, с горизонтальной осью диаграммы определяет угол крена. Диаграмма статической остойчивости строится для конкретного судна и соответствует определенным водоизмещению и положению Ц.В. по высо­те. Если у данного судна изменится водоизмещение или аппликата Ц.Т., то диаграмма статической остойчивости приобретает другой вид. Это обстоя­тельство всегда следует иметь в виду, и, прежде чем воспользоваться диаг­раммой для решения каких-либо вопросов, касающихся остойчивости дан­ного судна, необходимо обратить внимание на ее соответствие имеющейся нагрузке судна. Каждое судно должно быть снабжено комплектом диаграмм статической остойчивости, характеризующих остойчивость его при наибо­лее часто встречающихся случаях загрузки.

Диаграммы статической остойчивости отличаются большим разнообрази­ем форм кривых, но все они обладают некоторыми общими свойствами:

1. Начальный участок диаграммы статической остойчивости представляет собой прямую наклонную линию. Это видно, если приравнять две формулы восстанавливающего момента; метацентрическую формулу поперечной остой­чивости, применимую только для малых углов крена, и формулу восстанавли­вающего момента, справедливую для любых углов крена, т. е.

откуда:

2. Отрезок перпендикуляра, восста­новленного из точки на оси абсцисс, на­ходящейся на расстоянии одного радиа­на (57,3 град) от начала осей координат; до точки пересечения его с начальной касательном к кривой, определяет на ди­аграмме статической остойчивости по­перечную метацентрическую высоту h, взятую в масштабе плеч статической остойчивости. Однако графически определять метацентрическую высоту h по диаграмме статической остойчивости не рекомендуется, т.к. проведение ка­сательной к кривой не может быть выполнено с необходимой точностью.

Определение поперечной метацентрической высоты по ДСО

Построение диаграммы динамической остойчивости.

Динамическая остойчивость – остойчивость, при которой приложенный кренящий момент, действующий на судно мгновенно, приводя к возникновению углового ускорения и сил инерции.

При статическом приложении кренящего момента восстанавливающий момент постепенно увеличивается вместе с нарастанием угла крена, и эти моменты взаимно уравновешивают друг друга в течение всего процесса ста­тического накренения судна Движение судна происходит равномерно, без уг­ловых ускорении. Предположим теперь, что к судну, находящемуся в прямом положении, внезапно приложен кренящий момент, величина которого не связана с углом наклонения. Тогда график его действия можно изобразить на диаг­рамме статической остойчивости прямой линией ЕК параллельно оси (так действу­ет, например, на судно внезапно налетев­ший порыв ветра (шквал), обрыв тяжело­го груза, подвешенного на шкентеле вываленной за борт грузовой стрелы, обрыв

буксирного троса) Под действием этого момента судно быстро накреняется.

Угол крена, на который наклоняется судно при внезапном действии кренящего момента, называется динамическим углом крена θ_дин. Динамический угол крепа θ_дин определяют из условия равенства работ кренящего и восстанавливающего момента:

Отсюда получаем правило, которое используемся для графического решения уравнения (1) при сданном динамичес­ком кренящем моменте М_кр положение ординаты Вθ_дин подбирают таким образом, чтобы заштрихованные площади оказались равными. Тогда пересечение с осью ординаты Вθ_дин даст искомый угол динамическою крена. Определить динамический угол крена по диаграмме статической остойчивости можно лишь приближенно. Задачи, связанные с динамической остойчивостью решаются быстрее и точнее с помощью, так называемой диаграммы динамической остойчивости, которая представляем собой кривую, выражающую зависимость работы вос­станавливающего момента от угла крена. Построение такой диаграммы, являющейся интегральной кривой по от­ношению к диаграмме статической остойчивости, производится следующим образом. На оси абсцисс намечают несколько точек, соответствующих выб­ранным углам крена, и восстанавливают перпендикуляр до пересечения с кривой диаграммы статической остойчивости.

Диаграмма динамической остойчивости является интегральной кривой по отношению к диаграмме статической остойчивости и поэтому обладает свойствами, общими для всех интегральных кривых:

— Точки пересечения подынтегральной кривой (диаграммы статической остойчивости) с осью абсцисс отвечают точкам экстремума интегральной кривой (диаграммы динамической остойчивости);

— Точка максимума диаграммы статической остойчивости соответствует точке перегиба диаграммы динамической остойчивости;

— Точка максимума диаграммы динамической остойчивости соответствует углу заката диаграммы статической остойчивости;

— Любая ордината диаграммы динамической остойчивости, отвечающая некоторому углу крена θ, представляет в масштабе соответствующую этому углу крена площадь диаграммы статической остойчивости (заштрихована);

Задачи, решаемые с помощью диаграмм остойчивости.

Если момент, действующий на судно, находящееся в прямом положении, будет постепенно возрастать, то заштрихованная часть площади АВК (рис.1) будет также увеличиваться (из ус­ловия равенства работ кренящего и восстанавливающего моментов). При достижении некоторого значения кренящего момента М_{кр мах дин} вся площадь, расположенная выше линии кренящего момента, должна быть заштрихована. Динамический угол крена θ_{дин мах} станет равным статиче­скому углу крена θ_ст. соответствующему неустойчивому равновесию. Положение θ_ст определяет­ся второй точкой пересечения линии кренящего момента с диаграммой статической остойчивости, т.е. точкой К. При малейшем отклонении судна из этого положения равновесия работа кренящего момента превысит работу восстанавливающего — судно приобретет положительную угловую ско­рость и, выйдя из положения равновесия, неизбежно опрокинется. Внезапно приложенный кренящий момент, при котором динамический угол крена достигает значения статического угла неустойчивого равновесия, называется минимальным опрокидыва­ющим моментом М_опр. Прямая ОС (рис. 2) по мере увеличения кренящего момента может занять предельное положение, став касательной, проведенной из начала координат к диаграмме динамической остой­чивости. В этом случае абсцисса точки касания T₁ определит значение предельного угла динами­ческого крена θ_{дин мах}. Абсцисса точки T₁ на диаграмме динамической остойчивости будет соот­ветствовать абсциссе точки К на диаграмме статической остойчивости. Касательная ОС к диа­грамме динамической остойчивости характеризует ее предельный угол наклона α_пр к оси абсцисс, следовательно, точка пересечения этой касательной с перпендикуляром, восставленным к оси абс­цисс из точки А. соответствующей значению θ = 57.3° (1 радиан), дает отрезок АС, который опре­деляет минимальный опрокидывающий момент.

Теперь сопоставим значения предельных кренящих моментов — статических, постепенно возрастающих, и динамических, т. е. внезапных. Из сказанного выше следует, что предельный кре­нящий момент, действующий статически (его значение на рис.1 определяется ординатой точ­ки В), всегда больше предельного момента, действующего динамически (его значение определяет­ся ординатой ОЕ). Таким образом, для судна быстрое нарастание кренящего момента всегда более опасно, чем медленное.

До сих пор, рассматривая вопросы, связанные с действием внезапно приложенного креняще­го момента, мы исходили из предположения, что начальному положению судна соответствует угол крена, равный нулю (прямое положение). Между тем в практике эксплуатации судов бывают случаи, когда к началу действия внезапного кренящего момента судно уже находится в накренен­ном положении в результате действия какого-то кренящего момента. В этой ситуации при реше­нии задач динамической остойчивости возможны два случая: 1) судно плавает с начальным углом крена в том же направлении, в котором приложен внезапный кренящий момент; 2) судно имеет начальный крен в сторону, противоположную действию внезапного кренящего момента. При­мером первого случая служит действие на судно внезапно усилившегося ветра — шквала с навет­ренной стороны, примером второго — действие шквала с подветренной стороны.

Ограничимся рассмотрением способа решения задач по определению минимального опроки­дывающего момента для второго, более опасного случая.

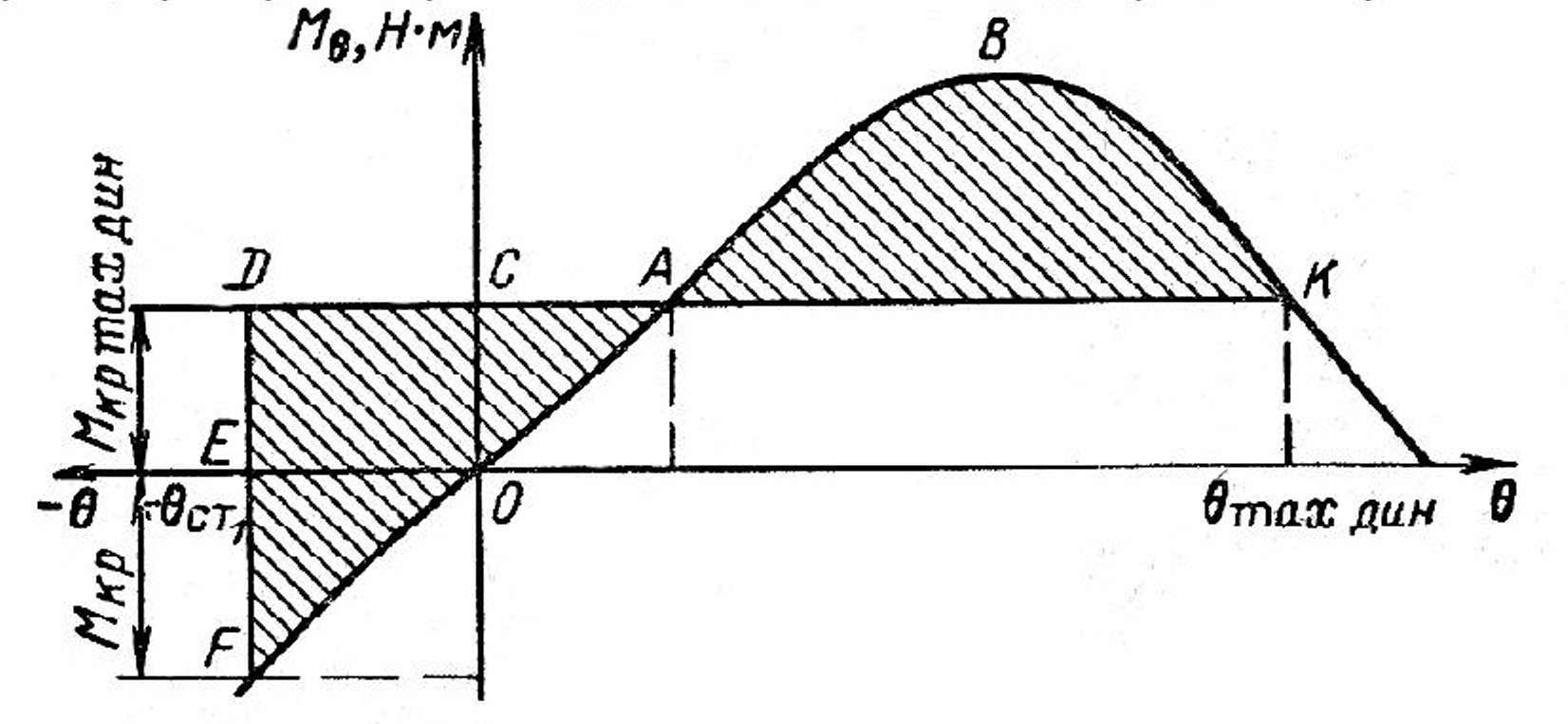
Допустим, что судно имеет крен – θ_ст1 созданный первоначально действующим моментом М_кр (рис.3). Кроме того, на судно действует внезапный кренящий момент М_{кр дин} в направле­нии, противоположном направлению М_кр, т. е. судно имеет крен на тот борт, со стороны которого подействовал внезапный кренящий момент.

В этом случае минимальный опрокидывающий момент определяют следующим образом.

Диаграмму статической остойчивости продолжают в область отрицательных значений абсцисс на участке, равном углу крена θ_ст1. Затем на оси абсцисс откладывают в соответствующем масштабе угол крена θ_ст1 через полученную точку Е проводят вертикальную линию до пересечения с диа­граммой (точка F) и продолжают ее вверх. После этого подбирают такое положение по высоте ли­нии DK. параллельной оси абсцисс, чтобы заштрихованные площади FDA и АВК оказались рав­ными. Найденная ордината ОС соответствует значению минимального опрокидывающего момента М_{кр мах дин} при наличии крена судна на угол θ_ст1 созданного первоначальным моментом М_кр. Абсцисса точки /С определяет угол крена θ_{дин мах} который при этом получит судно.

По диаграмме динамической остойчивости значения опрокидывающего момента и вызывае­мого им крена определяют следующим образом. Продолжают диаграмму

(рис. 4) в область отрицательных значений абсцисс на участке, равном углу θ_ст1. Затем на левой части оси абсцисс отмечают точку Е, соответствующую первоначальному углу крена θ_ст1, и через нее проводят вер­тикальную линию до пересечения с диаграммой

Сравнив ход решения задач с помощью двух диаграмм, видим, что использование диаграм­мы статической остойчивости для определения минимального опрокидывающего момента пред­ставляет некоторые трудности, но зато по этой диаграмме удобно находить динамический угол крена. По диаграмме динамической остойчивости, напротив, удобно определять минимальный оп­рокидывающий момент, но сложно найти точное положение точки Т и, следовательно, угол крена от действия этого момента. Очевидно, более точные результаты решения задачи можно получить в том случае, если минимальный опрокидывающий момент определять по диаграмме динамической остойчивости, а после этого, нанеся последний на диаграмму статической остойчивости, найти угол крена.

Источник

Динамическая остойчивость судна

В ряде случаев судоводителю приходится обращаться к вопросам динамической остойчивости судна. Конечно, в этих случаях судоводитель не решает сложных задач динамики судна – эта область деятельности ученных и исследователей в области теории судна. Но при решении отдельных задач, например при определении динамического крена, при определении предельных значений восстанавливающего момента, после которых судно опрокидывается, и при проверке соответствия параметров остойчивости принятым международным нормам без вопросов динамической остойчивости, хотя бы даже в упрощенной постановке, не обойтись.

Рассмотрение динамики наклонения судна в поперечной плоскости на этом уровне допустимо без учета инерции судна и потерь энергии на взаимодействие с жидкостью. В такой постановке достаточным оказывается использование понятия механической работы, совершаемой кренящим и восстанавливающим моментами, и сопоставлением их величин между собой.

Прежде чем перейти к специальным средствам теории динамической остойчивости, рассмотрим случай динамического накренения судна под действием ударной нагрузки от внезапного шквалистого ветра, пользуясь диаграммой статической остойчивости.

Предположим, что на плавающее без хода на поверхности спокойной воды судно внезапно обрушивается со стороны борта ветровой шквал. Этот шквал характеризуется возникновением ветровой нагрузки на надводной части судна и приводит к появлению внезапно действующего кренящего момента. Вид этого момента во времени представлены на Рисунке

Плечо кренящего момента от шквалистого ветра

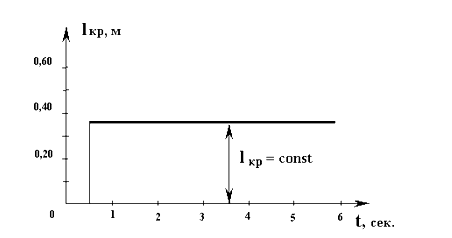
Можно с некоторой погрешностью считать, что величина этого кренящего момента слабо зависит от крена судна, т.е. считать его по крену постоянной величиной М_кр (θ) = const. Графическая зависимость такого кренящего момента, помещенная на диаграмму статической остойчивости, выглядит как горизонтальная линия с ординатой, равной величине этого момента (М_кр = М * _кр),

Крен судна от действия шквала

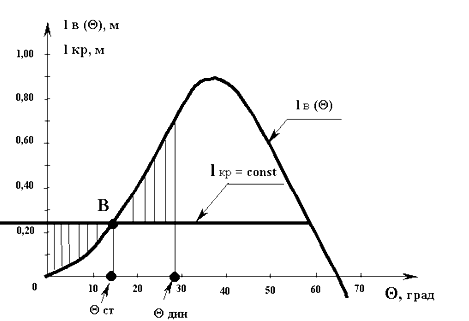
Теперь, если постараться проследить процесс наклонения судна на ДСО, от момента времени, когда восстанавливающий момент еще был равен нулю, то по мере развития (нарастания) угла крена судно будет разгоняться по угловой скорости вращения относительно продольной оси ОХ и приобретать инерцию. Дойдя на ДСО до точки пересечения обоих графиков (точка В на Рис. 9) судно не остановится и будет по инерции крениться дальше.

После точки В разница между обоими участвующими моментами становиться больше в пользу восстанавливающего момента (∆М = М_в – М_кр > 0), следовательно, этот результирующий момент будет совершать работу, пытаясь остановить его накренение. По-видимому, процесс динамического наклонения судна прекратится в момент времени, которому будет соответствовать равенство работ, совершенных каждым из моментов на своем пути.

Вспомним, что в механике работа при вращении тела вычисляется как произведение момента на угловой путь (в нашем случае это текущий угол крена судна). Для постоянного момента его работа вычисляется как произведение кренящего момента на угловой путь.

Для переменного по углу крена восстанавливающего момента работа вычисляется по общей формуле механики с использованием операции интегрирования переменного восстанавливающего момента по углу крена:

В судовых расчетах динамической остойчивости широко используется аналогия между величиной работы и площадью под графиком восстанавливающего момента. В данном рассмотренном случае удобно использовать подобную трактовку для нахождения момента окончания наклонения судна под действием шквала и соответствующий этому моменту динамический угол крена. Этот угол крена может быть найден на Рис. 9 путем взаимного подбора площадей под обоими графиками до их равенства.

Можно сделать вывод о том, что причиной больших динамических отклонений судна (это видно из сравнений крена θ_в и θ_g при одной и той же величине кренящего момента) является первоначальное «запаздывание» величины восстанавливающего момента, который нарастает постепенно от нуля, и его величина пока меньше величины кренящего момента. За это время, подходя к точке В, судно накапливает инерцию вращения, которую потом ему же самому приходится гасить с помощью увеличившегося к этому времени восстанавливающего момента. Результат этого процесса – значительно большие углы динамического крена по сравнению со статическим, либо даже опрокидывание судна.

Попутно здесь же можно сразу определить тот предельный кренящий динамический момент, действие которого судно уже удержать не сможет, обладая данной остойчивостью и ДСО.

Такой предельный момент называется опрокидывающим моментом (М_опр). Его значение находят на ДСО способом последовательных приближений, постепенно увеличивая величину кренящего момента (подбором более интенсивного шквала); наступает момент расчета, когда для площади под графиком кренящего момента М_кр (θ) уже не найдется равной по величине площади под графиком ДСО.

Как видно, решение задачи по нахождению опрокидывающего момента с помощью ДСО, сопряжено с необходимостью вычисления площадей и большим объемом вычислений. Для облегчения процедуры вычислений используется диаграмма динамической остойчивости (ДДО).

ДДО представляет собой графическую зависимость работы восстанавливающего момента от угла крена.

Такую диаграмму целесообразно построить заранее, сразу после построения ДСО, и использовать при решении динамических задач.

ДДО вычисляется на основе формулы (12), следовательно, график ДДО обладает свойствами интегральной кривой по отношению к графику подынтегральной функции, т.е. к ДСО. При углах крена θ = 0 и θ = θ₃, где М_в = 0, ДДО должна иметь экстремальные точки, т.е. минимум и максимум, соответственно, а при угле крена θ = θ_m, где М_в(θ) принимает максимальное значение – ДДО будет иметь точку перегиба. Важно отметить, что ДДО при всех вариантах остойчивости судна (при всех h₀) должна в начале координат иметь горизонтальную касательную.

Из прочих свойств ДДО можно отметить следующие:

так же будет возрастать угол заката, поскольку у соответствующих ДСО он увеличивается с ростом исходной МВ (h₀ испр ).

Диаграммы статической и динамической остойчивости

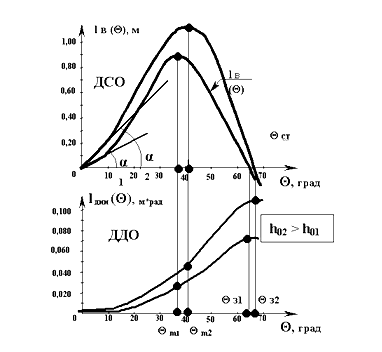
ДДО имеет две разновидности (как и соответствующие им ДСО):

Величину l_дин(θ * ) называют, по аналогии, плечом динамической остойчивости, хотя искать ему геометрическую интерпретацию не следует – эта величина получена чисто формальным путем. Размерность l_дин – [м · рад].

Однако, учитывая независимость l_дин от веса Р (и размеров) судна, возможно использовать её в задачах нормирования остойчивости, где удобно назначать универсальные константы-нормативы, которые могут использоваться на судах различного водоизмещения.

Судоводителю рекомендуют выполнять расчеты ДДО в табличной форме, где реализуется приближенный способ вычисления интеграла с переменным верхним пределом θ = θ * с использованием правила трапеций с повторениями (пример применения показан в Таблице:

Величины l_дин(θ) в четвертой колонке Табл. 1 получаются умножением значений частичной суммы Σ _част (из третьей колонки) на постоянный сомножитель, являющийся шагом интегрирования:Рассчитанная диаграмма статической остойчивости строится по значениям l_дин из четвертой колонки Табл.1 при значениях угла крена θ, взятых из первой колонки.

Источник