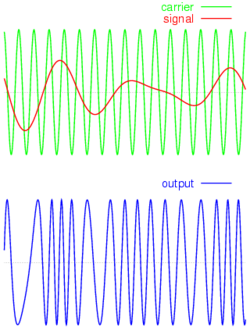
Частотная модуляция для чего нужна
Частотная модуляция
| Технологии модуляции п ·Аналоговая модуляция |
|---|
| AM · SSB · ЧМ(FM) · ЛЧМ · ФМ(PM) · СКМ |
| Цифровая модуляция |
| АМн · ФМн · КАМ · ЧМн · GMSK OFDM · COFDM · TCM |
| Импульсная модуляция |
| АИМ · ДМ · ИКМ · ΣΔ · ШИМ · ЧИМ · ФИМ |
| Расширение спектра |
| FHSS · DSSS |
| См. также: Демодуляция |
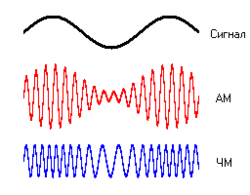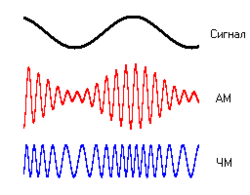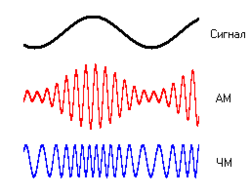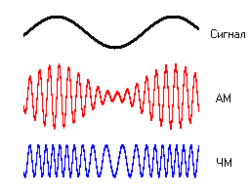
Частотная модуляция (ЧМ) — вид аналоговой модуляции, при котором информационный сигнал управляет частотой несущего колебания. По сравнению с амплитудной модуляцией здесь амплитуда остаётся постоянной.
Частотная модуляция была предложена Эдвином Армстронгом и запатентована им 26 декабря 1933 года.
Применение
Частотная модуляция применяется для высококачественной передачи звукового (низкочастотного) сигнала в радиовещании (в диапазоне УКВ), для звукового сопровождения телевизионных программ, передачи сигналов цветности в телевизионном стандарте SECAM, видеозаписи на магнитную ленту, музыкальных синтезаторах.
Высокое качество кодирования аудиосигнала обусловлено тем, что при ЧМ применяется большая (по сравнению с шириной спектра сигнала АМ) девиация несущего сигнала, а в приёмной аппаратуре используют ограничитель амплитуды радиосигнала для ликвидации импульсных помех.
См. также
Ссылки
Полезное
Смотреть что такое «Частотная модуляция» в других словарях:
частотная модуляция — ЧМ Модуляция синусоидального колебания путем изменения частоты в соответствии с амплитудными вариациями модулирующего сигнала. [http://www.vidimost.com/glossary.html] частотная модуляция [IEV number 314 08 02] EN frequency modulation process by… … Справочник технического переводчика
ЧАСТОТНАЯ МОДУЛЯЦИЯ — изменение частоты колебаний по заданному закону, медленное по сравнению с периодом этих колебаний (см. Модуляция колебаний). Преимущество частотной модуляции перед амплитудной модуляцией большая помехоустойчивость. Применяется для передачи звука… … Большой Энциклопедический словарь
ЧАСТОТНАЯ МОДУЛЯЦИЯ — ЧАСТОТНАЯ МОДУЛЯЦИЯ, форма радиопередачи, особый способ передачи радиоволн, излучаемых по сигналу радиовещания. Технический прием, который позволил сделать прием радиоволн совершенно свободным от статических помех. И хотя при этом ограничено… … Научно-технический энциклопедический словарь
ЧАСТОТНАЯ МОДУЛЯЦИЯ — вид модуляции колебаний, при к рой частота высокочастотного колебания изменяется во времени по закону, соответствующему передаваемому сигналу. Физический энциклопедический словарь. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983 … Физическая энциклопедия
частотная модуляция — изменение частоты колебаний по заданному закону, медленное по сравнению с периодом этих колебаний (см. Модуляция колебаний). Преимущество частотной модуляции перед амплитудной модуляцией большая помехоустойчивость. Применяется для передачи звука … Энциклопедический словарь
частотная модуляция — dažnio moduliavimas statusas T sritis automatika atitikmenys: angl. frequency modulation vok. Frequenzmodulation, f rus. частотная модуляция, f pranc. modulation de fréquence, f … Automatikos terminų žodynas
частотная модуляция — dažnio moduliavimas statusas T sritis Standartizacija ir metrologija apibrėžtis Veiksmas, kuriuo pagal tam tikrą dėsnį keičiamas nešlio dažnis. atitikmenys: angl. frequency modulation vok. Frequenzmodulation, f rus. частотная модуляция, f pranc.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
частотная модуляция — dažnio moduliavimas statusas T sritis fizika atitikmenys: angl. frequency modulation vok. Frequenzmodulation, f rus. частотная модуляция, f pranc. modulation de fréquence, f … Fizikos terminų žodynas
Частотная модуляция — вид модуляции колебаний (См. Модуляция колебаний), при которой частота несущего высокочастотного колебания изменяется во времени по закону, соответствующему передаваемому сигналу. Особенность Ч. м. высокая помехозащищенность. Ч. м.… … Большая советская энциклопедия
ЧАСТОТНАЯ МОДУЛЯЦИЯ — изменение частоты колебаний по заданному закону, медленное по сравнению с периодом этих колебаний (см. Модуляция колебаний). Преимущество Ч.м. перед амплитудной модуляцией большая помехоустойчивость. Применяется для передачи звука в телевидении и … Естествознание. Энциклопедический словарь
Теория радиоволн: аналоговая модуляция
Амплитудная модуляция
При амплитудной модуляции, огибающая амплитуд несущего колебания изменяется по закону, совпадающему с законом передаваемого сообщения. Частота и фаза несущего колебания при этом не меняется.
Одним из основных параметров АМ, является коэфициент модуляции(M).
Коэффициент модуляции — это отношение разности между максимальным и минимальным значениями амплитуд модулированного сигнала к сумме этих значений(%).
Проще говоря, этот коэффициент показывает, насколько сильно значение амплитуда несущего колебания в данный момент отклоняется от среднего значения.
При коэффициенте модуляции больше 1, возникает эффект перемодуляции, в результате чего происходит искажение сигнала.
Данный спектр свойственен для модулирующего колебания постоянной частоты.
На графике, по оси Х представлена частота, по оси У — амплитуда.
Для АМ, кроме амплитуды основной частоты, находящейся в центре, представлены также значения амплитуд справа и слева от частоты несущей. Это так называемые левая и правая боковые полосы. Они отнесены от частоты несущей на расстояние равное частоте модуляции.
Расстояние от левой до правой боковой полосы называют ширина спектра.
В нормальном случае, при коэффициенте модуляции
Частотная модуляция: теория, временная и частотная области
Хотя менее и интуитивно понятная, чем амплитудная модуляция, частотная модуляция (ЧМ, англ. FM) по-прежнему является довольно простым способом беспроводной передачи данных.
Мы все, по крайней мере, смутно знакомы с частотной модуляцией – это источник термина «FM радио». Если мы считаем частоту тем, что имеет мгновенное значение, а не как нечто, состоящее из нескольких периодов сигнала, деленных на соответствующий период времени, мы можем непрерывно изменять частоту в соответствии с мгновенной величиной низкочастотного сигнала.
Математика
В первой статье данной главы мы обсудили парадоксальную величину, называемую мгновенной частотой. Если вы считаете этот термин незнакомым или запутанным, вернитесь на эту страницу и прочитайте раздел «Частотная модуляция (ЧМ, англ. FM) и фазовая модуляция (ФМ, англ. PM)». Тем не менее, вы всё еще можете быть немного запутаны, и это понятно: идея мгновенной частоты нарушает основной принцип, согласно которому «частота» указывает, как часто сигнал завершает полный цикл: десять раз в секунду, миллион раз в секунду или сколько бы то ни было раз.
Мы не будем пытаться заниматься каким-либо тщательным или всесторонним рассмотрением мгновенной частоты в качестве математической концепции. (Если вы намерены подробно изучить эту проблему, вот академический документ, который должен помочь.) В контексте FM важно понять, что мгновенная частота естественно вытекает из того, что частота сигнала несущей изменяется непрерывно в ответ на модулирующую волну (т.е. низкочастотный сигнал). Мгновенное значение модулирующего сигнала влияет на частоту в определенный момент, а не на частоту одного или нескольких полных циклов.
На самом деле это верно только для аналоговой частотной модуляции; в цифровой ЧМ один бит соответствует дискретному числу циклов. Это приводит к интересной ситуации, когда более старая технология (аналоговая ЧМ) менее интуитивно понятна, чем более новая технология (цифровая частотная модуляция, также называемая частотной манипуляцией или FSK (Frequency Shift Keying)).
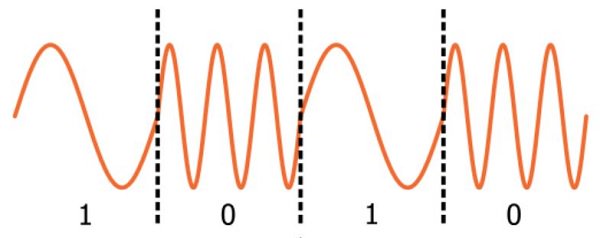
Единственное, что нам нужно здесь добавить, это индекс модуляции m. В предыдущей статье мы увидели, что индекс модуляции можно использовать для того, чтобы изменения амплитуды несущей были более или менее чувствительны к изменениям амплитуды низкочастотного сигнала. Его функция в FM аналогична: индекс модуляции позволяет нам точно настраивать интенсивность изменения частоты, которое возникает при изменении амплитуды низкочастотного сигнала.
Временна́я область
Давайте посмотрим на несколько сигналов во временной области. Ниже показана наша несущая 10 МГц:
Низкочастотным модулирующим сигналом будет синусоида 1 МГц, показанная ниже:
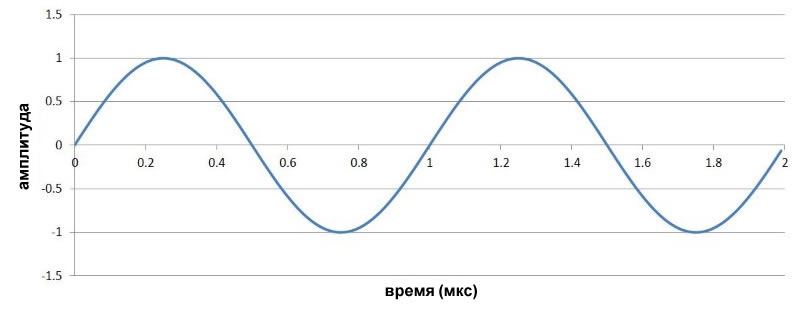
\[x_<чм>(t)=\sin((10\times10^6\times2\pi t)-\cos(1\times10^6\times2\pi t))\]
Результат показан ниже (красным показан низкочастотный модулирующий сигнал):
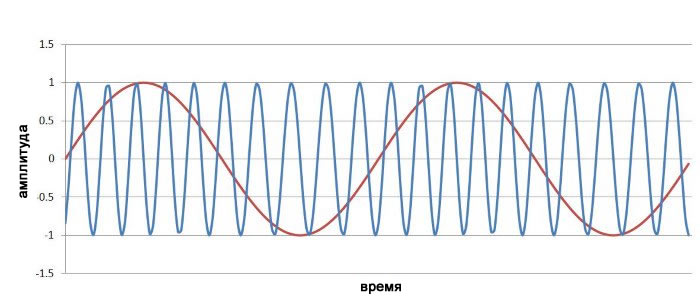
Похоже, что несущая не изменилась, но если присмотреться, пики немного ближе друг к другу, когда низкочастотный модулирующий сигнала приближается к своему максимальному значению. Итак, у нас есть частотная модуляция; но проблема заключается в том, что изменения модулирующего сигнала не создают достаточного изменения частоты несущей. Мы можем легко исправить эту ситуацию, увеличив индекс модуляции. Используем m =4.
\[x_<чм>(t)=\sin((10\times10^6\times2\pi t)-4\cos(1\times10^6\times2\pi t))\]
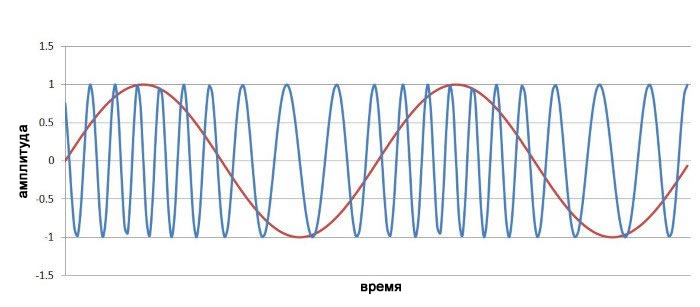
Теперь мы можем более четко видеть, как частота модулированной несущей непрерывно следует за мгновенным значением амплитуды низкочастотного модулирующего сигнала.
Частотная область
Формы AM и FM сигналов при одинаковых сигнале несущей и низкочастотном модулирующем сигнале выглядят совершенно по-разному. Поэтому интересно обнаружить, что AM и узкополосная FM дают аналогичные изменения в частотной области. (Узкополосная частотная модуляция предусматривает ограниченную полосу модулирующего сигнала и позволяет упростить анализ.) В обоих случая низкочастотный спектр (включая отрицательные частоты) переносится в полосу, которая простирается выше и ниже несущей частоты. В AM спектр самого низкочастотного модулирующего сигнала сдвигается вверх. В FM это спектр интеграла низкочастотного модулирующего сигнала, который появляется в полосе, окружающей несущую частоту.
Для модуляции, показанной выше, с m=1 мы получаем следующий спектр:
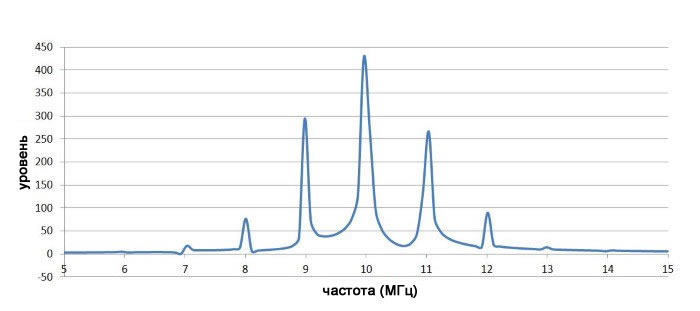
Следующий спектр соответствует m=4:
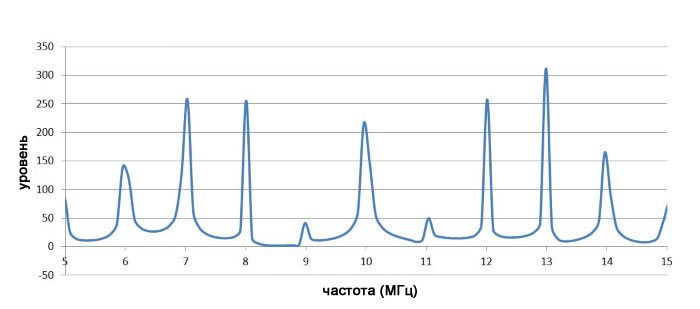
Это очень ясно показывает, что индекс модуляции влияет на частотные составляющие частотно-модулированного сигнала. Спектральный анализ частотной модуляции сложнее, чем для амплитудной модуляции; поэтому для частотно-модулированных сигналов трудно предсказать ширину полосы частот.