линейное время работы алгоритма означает что
Как найти временную сложность алгоритма
Вопрос
Как найти временную сложность алгоритма?
Что я сделал до публикации вопроса о SO?
Я прошел этот, этот и многие другие ссылки
Но нет, где я смог найти ясное и прямое объяснение того, как рассчитать сложность времени.
Что я знаю?
Скажите, что код такой же простой, как ниже:
Произнесите цикл, подобный приведенному ниже:
ОТВЕТЫ
Ответ 1
Как найти временную сложность алгоритма
Вы добавляете, сколько машинных инструкций он будет выполнять в зависимости от размера его ввода, а затем упростит выражение до самого большого (когда N очень велико) и может включать в себя любой упрощающий постоянный коэффициент.
Мы заинтересованы в производительности алгоритма по мере того, как N становится большим.
Рассмотрим два члена 2N и 2.
По этой причине мы бросаем все, кроме наибольших членов для больших N.
Традиционно нас интересует только производительность до постоянных факторов.
Это означает, что нам все равно, существует ли какая-то постоянная кратная разница в производительности, когда N велико. Во всяком случае, блок 2N не определен в первую очередь. Таким образом, мы можем умножить или разделить на постоянный коэффициент, чтобы перейти к простейшему выражению.
Ответ 2
Нижеприведенный ответ скопирован сверху (в случае, если прекрасная ссылка обанкротится)
Наиболее распространенной метрикой для расчета временной сложности является нотация Big O. Это устраняет все постоянные факторы, так что время работы можно оценить по отношению к N, когда N приближается к бесконечности. В общем, вы можете думать об этом так:
Постоянно. Время выполнения инструкции не изменится относительно N.
Является линейным. Время работы петли прямо пропорционально N. Когда N удваивается, время работы также выполняется.
Квадратично. Время работы двух петель пропорционально квадрату N. Когда N удваивается, время работы увеличивается на N * N.
Логарифмически. Время работы алгоритма пропорционально количеству раз, когда N можно разделить на 2. Это связано с тем, что алгоритм разделяет рабочую область пополам с каждой итерацией.
Является N * log (N). Время выполнения состоит из N циклов (итеративных или рекурсивных), которые являются логарифмическими, поэтому алгоритм представляет собой комбинацию линейных и логарифмических.
Обратите внимание, что ничто из этого не учитывает лучшие, средние и худшие меры. У каждого будет своя нотация Big O. Также обратите внимание, что это ОЧЕНЬ упрощенное объяснение. Big O является наиболее распространенным, но он также более сложным, чем я показал. Существуют и другие обозначения, такие как большая омега, маленькая о и большая тета. Вероятно, вы не столкнетесь с ними вне курса анализа алгоритмов.;)
Ответ 3
1. Введение
В информатике временная сложность алгоритма количественно определяет количество времени, затрачиваемое алгоритмом на выполнение, как функцию длины строки, представляющей входные данные.
2. Большая О запись
Временная сложность алгоритма обычно выражается с использованием больших обозначений O, что исключает коэффициенты и члены более низкого порядка. Когда выражено таким образом, говорят, что временная сложность описывается асимптотически, т.е. Размер входного сигнала стремится к бесконечности.
Например, если время, требуемое алгоритмом на всех входах размера n, составляет не более 5n 3 + 3n, асимптотическая сложность времени составляет O (n 3 ). Подробнее об этом позже.
Еще несколько примеров:
3. O (1) постоянное время:
Говорят, что алгоритм работает в постоянном времени, если ему требуется одинаковое количество времени независимо от размера ввода.
4. O (n) линейное время
Говорят, что алгоритм работает за линейное время, если его время выполнения прямо пропорционально размеру входа, то есть время растет линейно с увеличением размера входа.
Рассмотрим следующие примеры: ниже я линейно ищу элемент, который имеет временную сложность O (n).
5. O (log n) Логарифмическое время:
Говорят, что алгоритм работает в логарифмическом времени, если его время выполнения пропорционально логарифму входного размера.
6. O (n2) квадратичное время
Говорят, что алгоритм выполняется за квадратичное время, если его время выполнения пропорционально квадрату входного размера.
7. Некоторые полезные ссылки
Ответ 4
O (n): Time Сложность цикла рассматривается как O (n), если переменные цикла увеличиваются/уменьшаются на постоянную величину. Например, следующие функции имеют O (n) временную сложность.
O (n ^ c): временная сложность вложенных циклов равна количеству раз, когда выполняется самый внутренний оператор. Например, следующие контуры образцов имеют сложность времени O (n ^ 2)
Например, сортировка сортировки и сортировка вставки имеют сложность времени O (n ^ 2).
O (Logn) Время Сложность цикла рассматривается как O (Logn), если переменные цикла делятся/умножаются на постоянную величину.
Например, двоичный поиск имеет сложность времени O (Logn).
O (LogLogn) Время Сложность цикла рассматривается как O (LogLogn), если переменные цикла уменьшены/увеличены экспоненциально на постоянную величину.
Один пример анализа временной сложности
Анализ:
For i = 1, the inner loop is executed n times. For i = 2, the inner loop is executed approximately n/2 times. For i = 3, the inner loop is executed approximately n/3 times. For i = 4, the inner loop is executed approximately n/4 times. ……………………………………………………. For i = n, the inner loop is executed approximately n/n times.
Ответ 5
Сложность времени с примерами
Таким образом, сложность вышеуказанного псевдокода T (n) = 2 + 1 + max (1, 1 + 2) = 6. Таким образом, его большое oh по-прежнему остается постоянным T (n) = O (1).
Таким образом, его сложность T (n) = 1 + 4n + 1 = 4n + 2. Таким образом, T (n) = O (n).
Общее время выполнения
При анализе алгоритма существует некоторое общее время работы:
Взято из этой статьи. Очень хорошо объясненный должен дать прочитать.
Ответ 6
Когда вы анализируете код, вы должны анализировать его по очереди, подсчитывая каждую операцию/распознавая сложность времени, в конце концов, вы должны суммировать ее, чтобы получить целую картину.
Например, у вас может быть один простой цикл с линейной сложностью, но позже в этой же программе вы можете иметь тройной цикл с кубической сложностью, поэтому ваша программа будет иметь кубическую сложность. Здесь действует принцип роста.
Посмотрим, каковы возможности временной сложности алгоритма, вы можете увидеть порядок роста, о котором я говорил выше:
Ответ 7
Как и большинство вещей, коктейль может помочь нам понять.
O (N ^ 2)
O (N ^ 3)
Вы должны встретить всех остальных, и в ходе каждой встречи вы должны поговорить обо всех остальных в комнате.
Хост хочет что-то объявить. Они бросают рюмку и громко говорят. Каждый слышит их. Оказывается, неважно, сколько посетителей там, эта операция всегда занимает столько же времени.
O (log N)
Ведущий выложил всех за стол в алфавитном порядке. Где Дэн? Вы полагаете, что он должен быть где-то между Адамом и Мэнди (конечно, не между Мэнди и Заком!). Учитывая это, он между Джорджем и Мэнди? Нет. Он должен быть между Адамом и Фредом, а также между Синди и Фредом. И так далее. мы можем эффективно найти Дэна, посмотрев на половину набора, а затем на половину этого набора. В конечном счете мы смотрим на людей O (log_2 N).
O (N log N)
Вы можете найти, где сесть за столом, используя вышеприведенный алгоритм. Если к столу приходило большое количество людей, по одному за раз, и все это делали, что потребовалось бы O (N log N). Похоже, это время, необходимое для сортировки любой коллекции элементов, когда их нужно сравнивать.
Лучший/худший случай
Пространство и связь
Те же идеи могут быть применены для понимания того, как алгоритмы используют пространство или связь.
Теорема 2: Существуют сколь угодно длинные песни сложности O (1).
Доказательство: (из-за Кейси и полосы Солнца). Рассмотрим песни Sk, определенные по (15), но с
Ответ 8
Ответ 9
Ответ 10
Чтобы получить представление об алгоритме, я часто делаю это экспериментально. Просто измените вход N и посмотрите, сколько времени займет вычисление. Это требует некоторой мысли, поскольку big-O описывает худшую временную сложность алгоритма, и найти худший случай может быть сложным.
Для этого теоретически ваш подход кажется мне правдивым: пройдитесь по программе (всегда выбирайте самый сложный путь), добавляйте индивидуализированные времена и избавляйтесь от всех констант/факторов. Вложенные петли, прыжки и т.д. Могут сделать это довольно сложным, но я не могу думать о серебряной пуле, чтобы решить это в противном случае.
Сложность алгоритмов. Big O. Основы.
Развитие технологий привело к тому, что память перестала быть критическим ресурсом. Поэтому когда говорят об анализе сложности алгоритма, обычно подразумевают то, насколько быстро он работает.
Но ведь время выполнения алгоритма зависит от того, на каком устройстве его запустить. Один и тот же алгоритм запущенный на разных устройствах выполняется за разное время.
Big O показывает верхнюю границу зависимости между входными параметрами функции и количеством операций, которые выполнит процессор.
Распространённые сложности алгоритмов
Здесь рассмотрены именно распространённые виды, так как рассмотреть все варианты врядли возможно. Всё зависит от алгоритма, который вы оцениваете. Всегда может появится какая-то дополнительная переменная (не константа), которую необходимо будет учесть в функции Big O.
Означает, что вычислительная сложность алгоритма не зависит от входных данных. Однако, это не значит, что алгоритм выполняется за одну операцию или требует очень мало времени. Это означает, что время не зависит от входных данных.
Пример № 1.
У нас есть массив из 5 чисел и нам надо получить первый элемент.
Насколько возрастет количество операций при увеличении размера входных параметров?
Нинасколько. Даже если массив будет состоять из 100, 1000 или 10 000 элементов нам всеравно потребуется одна операция.
Пример № 2.
Сложение двух чисел. Функция всегда выполняет константное количество операций.
Пример № 3.
Размер массива. Опять же, функция всегда выполняет константной количество операций.
Означает, что сложность алгоритма линейно растёт с увеличением входных данных. Другими словами, удвоение размера входных данных удвоит и необходимое время для выполнения алгоритма.
Такие алгоритмы легко узнать по наличию цикла по каждому элементу массива.
Пример № 3.
Означает, что сложность алгоритма растёт логарифмически с увеличением входных данных. Другими словами это такой алгоритм, где на каждой итерации берётся половина элементов.
К алгоритмам с такой сложностью относятся алгоритмы типа “Разделяй и Властвуй” (Divide and Conquer), например бинарный поиск.
Означает, что удвоение размера входных данных увеличит время выполнения чуть более, чем вдвое.
Примеры алгоритмов с такой сложностью: Сортировка слиянием или множеством n элементов.
Означает, что удвоение размера входных данных увеличивает время выполнения в 4 раза. Например, при увеличении данных в 10 раз, количество операций (и время выполнения) увеличится примерно в 100 раз. Если алгоритм имеет квадратичную сложность, то это повод пересмотреть необходимость использования данного алгоритма. Но иногда этого не избежать.
Такие алгоритмы легко узнать по вложенным циклам.
Пример № 1.
В функции есть цикл в цикле, каждый из них проходит массив длиной n, следовательно сложность будет: O(n * n) = O(n 2 )
Зачем изучать Big O
Шпаргалка
Небольшие подсказки, которые помогут определить сложность алгоритма.
Полезные ссылки
Что такое временная сложность алгоритма?
Когда в детстве меня учили умножать числа, мне говорили, что смысл умножения в том, чтобы короче записать сумму. Например, 4 * 3 это то же, что 4 + 4 + 4.
Сведение умножения к сумме — самый простой, наивный алгоритм умножения. А теперь я возьму мой рабочий ноут и попробую перемножить этим способом какие-нибудь большие числа, например, 4 * 10000000000:
Если я попробую посчитать то же самое на калькуляторе, то замечу, что лаптоп отрабатывает заметно медленнее, несмотря на то, что он мощнее. Почему? Потому что для умножения чисел существует несколько алгоритмов, а я выбрала самый неэффективный из них. Ещё есть, например, метод Карацубы, или алгоритм на основе преобразования Фурье. В калькуляторах обычно используется второй, и он требует значительно меньше операций, чем наивный.
Как понять, быстро ли работает алгоритм? Можно попробовать измерить время напрямую:
Но мы обнаружим, что скорость зависит от производительности машины, от ее архитектуры и загруженности в момент выполнения программы. Поэтому физическое время никак не поможет нам оценить эффективность алгоритма.
Чтобы уйти от физических свойств вычислителя, используют понятие сложности. Асимптотическая сложность алгоритма — это то, как изменяется время исполнения в зависимости от объема входных данных. В этом определении намеренно не учитывается то, на каком устройте выполняется алгоритм: это может быть компьютер, калькулятор или даже человек. Такой абстрактный вычислитель называют машиной Тьюринга.
При этом разделяют сложность алгоритма в худшем и лучшем случае. Представьте, что мы хотим проверить, есть ли в списке число 42. Мы проверяем первый элемент на равенство 42, второй, третий… В лучшем случае первый элемент окажется искомым. В худшем — последний. Поэтому обычно рассматривают сложность алгоритма в наилучшем, наихудшем случае, и в среднем. Как правило, пессимистическая оценка самая интересная из всех, потому что позволяет планировать объем ресурсов.
Временную сложность алгоритма в худшем случае выражают с использованием нотации «O» большое. В этом случае из рассмотрения исключают члены меньшего порядка и говорят об изменении используемых ресурсов при стремлении размера входа к бесконечности. Например, если время, которое нужно алгоритму для выполнения работы, для всех входов длины n не превосходит 5n^3 + 3n, то асимптотическая временная сложность равна O(n^3).
Рассмотрим несколько примеров
Время, которое не зависит от объема входных данных, или постоянное время. За постоянное время можно получить элемент массива по индексу или добавить элемент в связный список.
Алгоритм, в котором мы идём по списку, чтобы узнать, есть ли в нем значение 42, в худшем случае требует O(n) операций, где n — длина списка. Такую же сложность имеет сравнение строк, потому что по сути оно тоже требуют обхода всей строки.
O(log n)
Проверить, есть ли значение 42 в списке, можно быстрее, чем за O(n), если список отсортирован. Тогда можно проверить на равенство элемент из середины списка. Если он равен 42, то останавливаемся. Если больше — значит, слева можно не искать, там значения только меньше. Будем продолжать проверку, выбирая каждый раз элемент из середины оставшегося отрезка. Этот алгоритм называют бинарным поиском и он имеет логарифмическую сложность, потому что количество вариантов уменьшается каждый раз на 2, как функция, обратная степенной (она же логарифм).
O(n log n)
Можно показать, что большинство алгоритмов сортировки имеют сложность n log(n). За время n log(n) работают сортировка слиянием, кучей, и быстрая сортировка. Еще есть теорема, которая говорит, что если сортировка основана на сравнении элементов, то быстрее, чем за n log(n) отсортировать элементы не получится.
За время n^2 работает обход двумерного массива, это можно представить себе как обход таблицы n * n. И ещё за это же время работают некоторые не очень эффективные по времени алгоритмы сортировки, например, сортировка пузырьком.
Для разработчика важно иметь интуицию насчет временной сложности алгоритмов, потому что за счет неэффективности вычислений можно загубить производительность самого мощного железа, как это случилось, когда калькулятор побил мой мощный ноутбук. Поэтому этой науке уделяется большое внимание в разработке. 95%, что на собеседовании вам предложат алгоритмическую задачу и попросят оценить время выполнения вашего решения.
Если вы хотите углубиться в теорию алгоритмов, то я советую специализацию Алгоритмы и структуры данных на Курсере. Теория здесь изложена доступно и в курсе есть задачи, чтобы набить руку. А еще есть Стенфордский учебник по теории сложности, он написан замечательным языком и в нем прекрасные примеры.
Оценка сложности алгоритмов, или Что такое О(log n)
Авторизуйтесь
Оценка сложности алгоритмов, или Что такое О(log n)
Наверняка вы не раз сталкивались с обозначениями вроде O(log n) или слышали фразы типа «логарифмическая вычислительная сложность» в адрес каких-либо алгоритмов. И если вы хотите стать хорошим программистом, но так и не понимаете, что это значит, — данная статья для вас.
Оценка сложности
Сложность алгоритмов обычно оценивают по времени выполнения или по используемой памяти. В обоих случаях сложность зависит от размеров входных данных: массив из 100 элементов будет обработан быстрее, чем аналогичный из 1000. При этом точное время мало кого интересует: оно зависит от процессора, типа данных, языка программирования и множества других параметров. Важна лишь асимптотическая сложность, т. е. сложность при стремлении размера входных данных к бесконечности.
Примеры
O(n) — линейная сложность
Такой сложностью обладает, например, алгоритм поиска наибольшего элемента в не отсортированном массиве. Нам придётся пройтись по всем n элементам массива, чтобы понять, какой из них максимальный.
O(log n) — логарифмическая сложность
Простейший пример — бинарный поиск. Если массив отсортирован, мы можем проверить, есть ли в нём какое-то конкретное значение, методом деления пополам. Проверим средний элемент, если он больше искомого, то отброс им вторую половину массива — там его точно нет. Если же меньше, то наоборот — отброс им начальную половину. И так будем продолжать делить пополам, в итоге проверим log n элементов.
O(n 2 ) — квадратичная сложность
Бывают и другие оценки по сложности, но все они основаны на том же принципе.
Аналогично проводят оценку и по памяти, когда это важно. Однако алгоритмы могут использовать значительно больше памяти при увеличении размера входных данных, чем другие, но зато работать быстрее. И наоборот. Это помогает выбирать оптимальные пути решения задач исходя из текущих условий и требований.
Наглядно
Время выполнения алгоритма с определённой сложностью в зависимости от размера входных данных при скорости 10 6 операций в секунду:
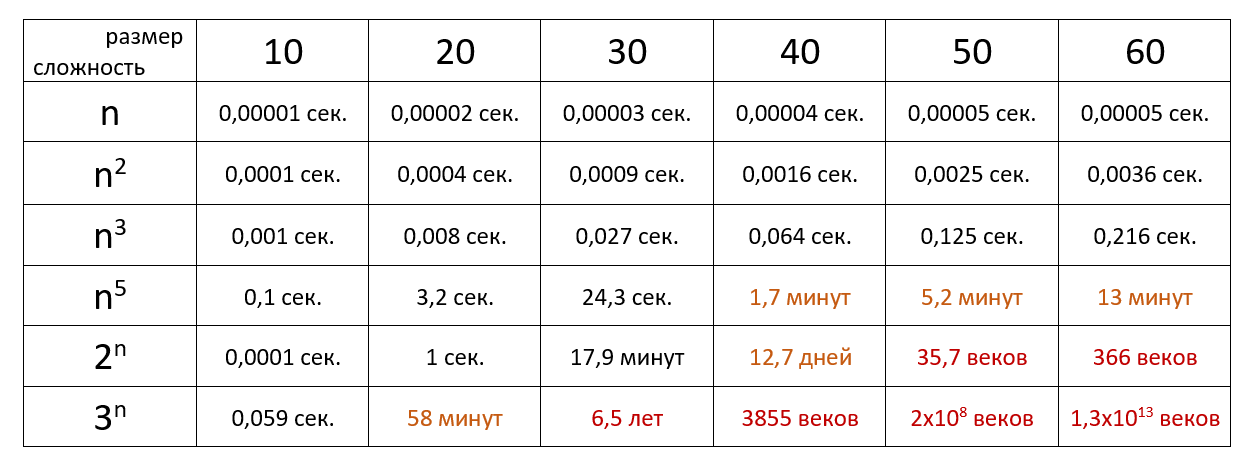
Если хочется подробнее и сложнее, заглядывайте в нашу статью из серии «Алгоритмы и структуры данных для начинающих».
«О» большое: объяснение для тех, у кого нет диплома по информатике
Перевод статьи «Big-O For The Non-CS Degree».
Вам когда-нибудь было любопытно, почему одни алгоритмы работают быстрее других? Да, я раньше тоже как-то не задумывался над этим, а зря. Объяснить это различие в скорости помогает «О» большое.
Что такое это ваше «О» большое?
Это способ измерить, сколько по времени будет выполняться алгоритм и насколько хорошо он масштабируется относительно размера набора данных. В общем, «О» большое служит для измерения эффективности алгоритмов.
Допустим, у нас есть список из 15 человек и мы хотим найти в этом списке всех людей, чье имя начинается на «Т». Для сортировки можно использовать разные алгоритмы, причем все они будут отличаться по уровню сложности. И некоторые из них будут более производительными, чем другие.
А теперь представьте, что имен у нас не 15, а миллион. Как вы думаете, насколько такой прирост данных повлияет на производительность алгоритмов? Ответ на этот вопрос можно найти при помощи нотации «О» большое.
«О» большое бывает разным:
Давайте рассмотрим каждый из вариантов.
O(1) — постоянное время
Если у алгоритма постоянная временная сложность, значит, размер передаваемых данных никак не влияет на его производительность. Время выполнения останется неизменным, какой бы набор данных вы ему ни передали. То есть, это может быть список из 5 элементов, а может быть и из тысячи — не важно. Алгоритм с такой нотацией очень масштабируемый.
Допустим, у нас есть массив чисел и мы хотим найти второй элемент в этом списке. Не важно, насколько длинный наш список: поиск второго элемента всегда будет занимать одинаковое время.
Оба вызова функции будут выполнены за одинаковое время, несмотря на то, что один список больше другого.
O(log n) — логарифмическое время
Если у алгоритма логарифмическая временная сложность, это значит, что время выполнения будет зависеть от логарифма размера входящих данных. Хорошим примером может послужить бинарный поиск. Вы последовательно делите набор данных надвое, пока не достигнете нужной точки.
В примере, приведенном ниже, мы перебираем в цикле список чисел и проверяем, равен ли элемент на серединной позиции определенному значению. Если нет, мы отделяем половину чисел, выбираем новую серединную позицию и проверяем снова. Это продолжается, пока мы не найдем нужное нам число или пока в массиве не кончатся числа.
O(n) — линейное время
Линейная временная сложность алгоритма означает, что время его работы находится в прямой зависимости от размера входящих данных. Если количество элементов наборе данных растет, пропорционально растет и время работы.
Посмотрите на пример, приведенный ниже. Мы используем цикл for для вывода на экран каждого элемента массива. Чем больше элементов, тем дольше работает алгоритм.
Если бы мы добавили еще один элемент в массив junkFood, время работы функции возросло бы пропорционально.
O(n log n) — линейно-логарифмическое время
Если временная сложность алгоритма описывается линейно-логарифмической функцией, то, как вы можете догадаться, она занимает промежуточное положение между линейной и логарифмической сложностью. В таком алгоритме тоже применяется подход «разделяй и властвуй», как в алгоритмах с логарифмической сложностью. Но здесь набор данных сначала разбивается на подсписки, состоящие максимум из двух элементов (т. е., на пары).
В нашем примере мы взяли список из 20 элементов. Эти элементы сначала будут разбиты попарно, на 10 подсписков. И здесь вступает в игру «линейная» часть функции. Когда все элементы разбиты попарно, мы сортируем каждую отдельную пару, а затем последовательно объединяем отсортированные пары, продолжая сортировать получившийся результат. Пример алгоритма с линейно-логарифмической временной сложностью — сортировка слиянием.
O(n^2) — квадратичное время
Квадратичная временная сложность — это когда производительность алгоритма прямо пропорциональна размеру входных данных в квадрате. Проще говоря, это линейная временная сложность в квадрате.
Если, к примеру, в нашем наборе данных есть 2 элемента, за время работы алгоритма будет выполнено 4 операции. Если в наборе 4 элемента, то операций будет 16. При 6 элементах будет 36 операций, и так далее.
В нашем примере мы применяем алгоритм сортировки пузырьком, имеющий квадратичную временную сложность. Мы создаем вложенный цикл внутри другого цикла, сортируем наш массив и меняем местами смежные элементы, если они идут в неправильном порядке.
Это очень хороший метод работы для маленьких объемов данных, потому что такой алгоритм легко реализовать. Но при увеличении объема входных данных время работы будет расти экспоненциально. Очевидно, что подобные решения не годятся для масштабирования.
O(2^n) — экспоненциальное время
Экспоненциальную временную сложность мы можем наблюдать в алгоритмах, где количество вычислений удваивается при добавлении каждого нового элемента в набор данных. Так происходит, например, в брутфорс-решениях с использованием рекурсии. На маленьких наборах данных все работает отлично, но с увеличением числа элементов в наборе время выполнения может выйти из-под контроля.
Хорошим примером может служить рекурсивный расчет чисел Фибоначчи — такой, как в коде, приведенном ниже.
O(n!) — факториальное время
Факториальная временная сложность — это когда количество вычислений в алгоритме прирастает факториально в зависимости от размера набора данных. Это, пожалуй, наихудший тип временной сложности, потому что количество операций возрастает до астрономических пределов даже при небольшом увеличении набора данных.
Как видите, число операций ужасно растет при каждом добавлении элемента в набор.
Хорошим примером алгоритма с факториальной временной сложностью может послужить простая рекурсивная функция. Эта функция принимает число в качестве входных данных и умножает его на факториал числа, меньшего на единицу. (В общем, стандартная функция для вычисления факториала числа, переданного в качестве инпута, — прим. ред. Techrocks). Как видите, время работы функции при незначительном увеличении входных данных растет просто катастрофически.
Итоги
Когда ищете алгоритмическое решение задачи, важно учитывать временную сложность выбранного алгоритма. Не все алгоритмы одинаково производительны: некоторые могут быть эффективнее других в зависимости от величины обрабатываемого объема данных. А для сравнения эффективности алгоритмов применяется нотация большого «О».