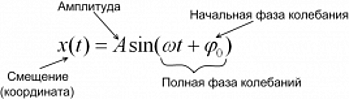круговая частота колебаний в чем измеряется
Угловая частота
Углова́я частота́ (синонимы: радиальная частота, циклическая частота, круговая частота) — скалярная физическая величина, мера частоты вращательного или колебательного движения. В случае вращательного движения, угловая частота равна модулю вектора угловой скорости. В системах СИ и СГС угловая частота выражается в радианах в секунду, её размерность обратна размерности времени (радианы безразмерны). Угловая частота является производной по времени от фазы колебания:
Другое распространённое обозначение
Угловая частота в радианах в секунду выражается через частоту f (выражаемую в оборотах в секунду или колебаниях в секунду), как
В случае использования в качестве единицы угловой частоты градусов в секунду связь с обычной частотой будет следующей:
См. также
Полезное
Смотреть что такое «Угловая частота» в других словарях:
угловая частота — периодических колебаний; угловая частота; отрасл. круговая частота Число периодов колебаний в 2π единиц времени. угловая частота синусоидального электрического тока; угловая частота Частота синусоидального электрического тока, умноженная на 2π … Политехнический терминологический толковый словарь
угловая частота — Скорость изменения фазы синусоидального электрического тока, равная частоте синусоидального электрического тока, умноженной на 2π. Примечание — Аналогично определяют угловые частоты синусоидальных электрического напряжения,… … Справочник технического переводчика
УГЛОВАЯ ЧАСТОТА — (круговая частота), число колебаний, совершаемое за 2p секунд. Угловая частота w=2pn=2p/T, где n число колебаний в 1 с., T период колебаний. Угловая частота при вращательном движении число оборотов, совершаемое вращающимся твердым телом за 1 с.,… … Современная энциклопедия
Угловая частота — (круговая частота), число колебаний, совершаемое за 2p секунд. Угловая частота w=2pn=2p/T, где n число колебаний в 1 с., T период колебаний. Угловая частота при вращательном движении число оборотов, совершаемое вращающимся твердым телом за 1 с.,… … Иллюстрированный энциклопедический словарь
угловая частота — 3.1.2 угловая частота w (angular frequency), рад/с: Циклическая частота, умноженная на 2π. Источник … Словарь-справочник терминов нормативно-технической документации
угловая частота — (круговая частота), число колебаний, совершаемых за 2π единиц времени. Угловая частота ω = 2πn = 2π/T, где ν число колебаний в единицу времени, Т период колебаний. Обычно используемая единица времени секунда; тогда угловая частота измеряется в … Энциклопедический словарь
угловая частота — kampinis dažnis statusas T sritis fizika atitikmenys: angl. angular frequency; cyclic frequency; radian frequency vok. Kreisfrequenz, f; Winkelfrequenz, f rus. круговая частота, f; угловая частота, f; циклическая частота, f pranc. fréquence… … Fizikos terminų žodynas
угловая частота — kampinis dažnis statusas T sritis automatika atitikmenys: angl. angular frequency; circular frequency vok. Kreisfrequenz, f; Winkelfrequenz, f rus. круговая частота, f; угловая частота, f pranc. fréquence angulaire, f; fréquence circulaire, f … Automatikos terminų žodynas
угловая частота — kampinis dažnis statusas T sritis Standartizacija ir metrologija apibrėžtis Virpesio fazės kitimo sparta, išreiškiama formule: ω = 2πf; čia f – dažnis. Kampinio dažnio ω matavimo vienetas yra rad/s (radianas per sekundę), o dažnio f – Hz (hercas) … Penkiakalbis aiškinamasis metrologijos terminų žodynas
Круговая частота
Углова́я частота́ (синонимы: радиальная частота, циклическая частота, круговая частота) — скалярная величина, мера частоты вращательного или колебательного движения. В случае вращательного движения, угловая частота равна модулю вектора угловой скорости. В системах СИ и СГС угловая частота выражается в радианах в секунду, её размерность обратна размерности времени (радианы безразмерны). Угловая частота является производной по времени от фазы колебания:
Угловая частота в радианах в секунду выражается через частоту f (выражаемую в оборотах в секунду или колебаниях в секунду), как
В случае использования в качестве единицы угловой частоты градусов в секунду связь с обычной частотой будет следующей:
Наконец, при использовании оборотов в секунду угловая частота совпадает с частотой вращения:
Введение циклической частоты (в её основной размерности — радианах в секунду) позволяет упростить многие формулы в теоретической физике и электронике. Так, резонансная циклическая частота колебательного LC-контура равна 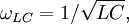
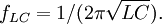
См. также
Полезное
Смотреть что такое «Круговая частота» в других словарях:
круговая частота — угловая частота циклическая частота Величина ω=2πf=2π/Т, где f частота, Т период колебания. [Система неразрушающего контроля. Виды (методы) и технология неразрушающего контроля. Термины и определения (справочное пособие). Москва 2003… … Справочник технического переводчика
КРУГОВАЯ ЧАСТОТА — то же, что угловая частота … Большой Энциклопедический словарь
круговая частота — то же, что угловая частота. * * * КРУГОВАЯ ЧАСТОТА КРУГОВАЯ ЧАСТОТА, то же, что угловая частота (см. УГЛОВАЯ ЧАСТОТА) … Энциклопедический словарь
круговая частота — угловая частота периодических колебаний; угловая частота; отрасл. круговая частота Число периодов колебаний в 2π единиц времени … Политехнический терминологический толковый словарь
круговая частота — kampinis dažnis statusas T sritis fizika atitikmenys: angl. angular frequency; cyclic frequency; radian frequency vok. Kreisfrequenz, f; Winkelfrequenz, f rus. круговая частота, f; угловая частота, f; циклическая частота, f pranc. fréquence… … Fizikos terminų žodynas
круговая частота — kampinis dažnis statusas T sritis automatika atitikmenys: angl. angular frequency; circular frequency vok. Kreisfrequenz, f; Winkelfrequenz, f rus. круговая частота, f; угловая частота, f pranc. fréquence angulaire, f; fréquence circulaire, f … Automatikos terminų žodynas
круговая частота — kampinis dažnis statusas T sritis Standartizacija ir metrologija apibrėžtis Virpesio fazės kitimo sparta, išreiškiama formule: ω = 2πf; čia f – dažnis. Kampinio dažnio ω matavimo vienetas yra rad/s (radianas per sekundę), o dažnio f – Hz (hercas) … Penkiakalbis aiškinamasis metrologijos terminų žodynas
КРУГОВАЯ ЧАСТОТА — то же, что угловая частота … Большой энциклопедический политехнический словарь
КРУГОВАЯ ЧАСТОТА — то же, что угловая частота … Естествознание. Энциклопедический словарь
круговая частота — угловая скорость … Словарь русских синонимов по технологиям автоматического контроля
Циклическая частота
Определение циклической частоты
Циклической (угловой, радиальной круговой) частотой называют скалярную физическую величину, которая служит мерой вращательного или колебательного движения.
Угловая скорость при равномерном движении по окружности является постоянной величиной, в этом случае ее называют циклической частотой.
Циклическая частота гармонических колебаний
Колебательные движения играют важную роль в самых разных вопросах физики. Рассмотрим колебания материальной точки. При колебаниях материальная точка через равные промежутки времени проходит через одно и то же положение при движении в одном направлении.
Если начальная фаза колебаний равна нулю, то
Период (T) колебаний и циклическая частота связаны формулой:
Единицей измерения циклической частоты в Международной системе единиц (СИ) является радиан, деленный на секунду:
Размерность циклической частоты:
Примеры задач с решением
Решение. Запишем уравнение гармонических колебаний точки, если известно, что они происходят по оси X:
Максимальное значение скорости (амплитуда скорости) равна:
Следовательно, циклическую частоту колебаний находим как:
Вычислим величину циклической частоты:
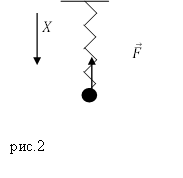
Решение. Сделаем рисунок.
тогда уравнение (2.2) преобразуется к виду:
Общее решение уравнения (2.4) это:
Значит, груз на пружине совершает колебания, циклическая частота которых равна:
Амплитуда, период, частота колебаний.
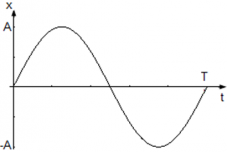
Амплитуда колебаний (лат. amplitude — величина) — это наибольшее отклонение колеблющегося тела от положения равновесия.
Для маятника это максимальное расстояние, на которое удаляется шарик от своего положения равновесия (рисунок ниже). Для колебаний с малыми амплитудами за такое расстояние можно принимать как длину дуги 01 или 02, так и длины этих отрезков.
Амплитуда колебаний измеряется в единицах длины — метрах, сантиметрах и т. д. На графике колебаний амплитуда определяется как максимальная (по модулю) ордината синусоидальной кривой, (см. рис. ниже).
Период колебаний.
Период колебаний — это наименьший промежуток времени, через который система, совершающая колебания, снова возвращается в то же состояние, в котором она находилась в начальный момент времени, выбранный произвольно.
Другими словами, период колебаний (Т) — это время, за которое совершается одно полное колебание. Например, на рисунке ниже это время, за которое грузик маятника перемещается из крайней правой точки через точку равновесия О в крайнюю левую точку и обратно через точку О снова в крайнюю правую.
За полный период колебаний, таким образом, тело проходит путь, равный четырем амплитудам. Период колебаний измеряется в единицах времени — секундах, минутах и т. д. Период колебаний может быть определен по известному графику колебаний, (см. рис. ниже).
Понятие «период колебаний», строго говоря, справедливо, лишь когда значения колеблющейся величины точно повторяются через определенный промежуток времени, т. е. для гармонических колебаний. Однако это понятие применяется также и для случаев приблизительно повторяющихся величин, например, для затухающих колебаний.
Частота колебаний.
Частота колебаний — это число колебаний, совершаемых за единицу времени, например, за 1 с.
Единица частоты в СИ названа герцем (Гц) в честь немецкого физика Г. Герца (1857-1894). Если частота колебаний (v) равна 1 Гц, то это значит, что за каждую секунду совершается одно колебание. Частота и период колебаний связаны соотношениями:

В теории колебаний пользуются также понятием циклической, или круговой частоты ω. Она связана с обычной частотой v и периодом колебаний Т соотношениями:

Циклическая частота — это число колебаний, совершаемых за 2π секунд.
17. Механика  Читать 0 мин.
Читать 0 мин.
17.547. Механические колебания
Колебания ― это процесс, при котором состояние системы изменяется, повторяясь во времени, и смещаясь то в одну, то в другую сторону относительно состояния равновесия.
Период ― это время, через которое повторяются показатели системы, т. е. система совершает одно полное колебание. Период изменяется в секундах.
N ― количество колебаний;
ω ― циклическая частота [рад/с];
Гармонические колебания ― колебания, в которых физические величины изменяются по закону синуса или косинуса. Кинематическое уравнение гармонических колебаний имеет вид:
ω ― циклическая частота [рад/с];
φ0 ― начальная фаза колебаний, [рад];
Смещение (x) ― это отклонение тела от положения равновесия. Смещение также является координатой тела, если отсчитывать ее от положения равновесия.
Амплитуда колебаний (A) ― максимальное отклонение колеблющейся величины от положения равновесия, т. е. максимальное смещение равно амплитуде колебаний xmax = A.
Начальная фаза колебаний (φ0) определяет смещение в начальный момент времени, выраженное в радианах.
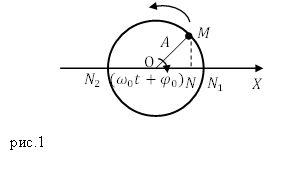
Фаза колебаний (φ) или полная фаза колебаний, определяет смещение в данный момент времени, выраженное в радианах. Фаза колебаний равна φ = ωt + φ0, где
φ ― полная фаза колебаний [рад];
φ0 ― начальная фаза колебаний, [рад];
ω ― циклическая частота [рад/с];
Пример анализа гармонических колебаний точки
Рассмотрим гармонические колебания, в которых уравнение движения точки имеет вид x(t) = Asin(ωt), где
ω ― циклическая частота [рад/с].
График колебания координаты точки имеет вид:
Определим уравнение и график колебания скорости. Скорость ― это производная координаты по времени: v = xt‘, где
v ― скорость движения точки [м/с];
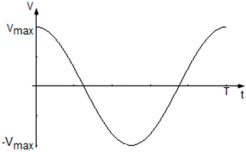
Так как закон изменения координаты нам известен x(t) = Asin(ωt), скорость движения колеблющейся точки: v = xt‘ = |Asin(ωt)|’t = Acos(ωt).
Уравнение скорости точки равно v(t) = Acos(ωt), где
v ― скорость движения точки [м/с];
ω ― циклическая частота [рад/с];
Сравнив уравнение v(t) = Aωcos(ωt) с кинематическим уравнением гармонических колебаний, легко заметить, что Aω ― амплитуда изменения скорости, а ωt ― фаза колебаний скорости. Таким образом, максимальное значение скорости равно vmax = Aω, и оно достигается при | cos(ωt) | = 1, т. е. тогда, когда фаза колебаний скорости равна φ = πn, где n = 0, 1, 2, … N.
График колебания скорости точки имеет вид:
Аналогично определяются уравнение и график колебания ускорения точки, которая движется по гармоническому закону.
Ускорение ― это производная скорости по времени: a = vt‘, где
a ― ускорение движения точки [м/с2];
v ― скорость движения точки [м/с];
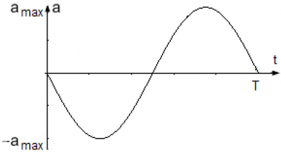
Так как закон изменения скорости был определен выше v(t) = Aωcos(ωt), определим ускорения движения колеблющейся точки: a = vt‘ = [Aωcos(ωt)]t‘ = –Aω2sin(ωt).
Уравнение ускорения точки равно a(t) = –Aω2sin(ωt), где
a ― ускорение движения точки [м/с2];
ω ― циклическая частота [рад/с];
Модуль ускорения точки максимален, когда |sin(ωt)| = 1 ― тогда же, когда достигает максимума смещение точки. Максимальное ускорение, т. е. амплитуда ускорения точки равна amax = Aω2.
График колебания ускорения точки имеет вид:
Во время гармонических колебаний, формы энергии колебательной системы все время находятся в процессе взаимной трансформации. В механической колебательной системе преобразуется механическая энергия: потенциальная энергия ― в кинетическую, а затем кинетическая энергия ― вновь в потенциальную. Полная механическая энергия колеблющейся системы постоянна, и в любой момент времени справедлив закон сохранения энергии E = EП + EK, где
E ― полная механическая энергия системы, E = const, [Дж];
EП ― потенциальная энергия системы, изменяющаяся во времени, [Дж];
EK ― кинетическая энергия системы, изменяющаяся во времени, [Дж].
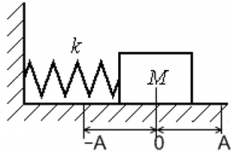
Рассмотрим изменение потенциальной энергии пружинного маятника, который колеблется по гармоническому уравнению x(t) = Asin(ωt).
EП ― потенциальная энергия деформированной пружины, [Дж];
k ― коэффициент упругости пружины [Н/м];
x ― деформация пружины (величина ее удлинения или сжатия) [м].
EП ― потенциальная энергия пружинного маятника, [Дж];
k ― коэффициент упругости пружины [Н/м];
ω ― циклическая частота [рад/с];
EПmax ― максимальная потенциальная энергия пружинного маятника, [Дж];
k ― коэффициент упругости пружины [Н/м];
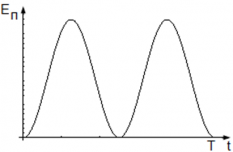
Потенциальная энергия пружинного маятника равна нулю, когда sin(ωt) = 0 ― когда маятник проходит положение равновесия, и максимальна, когда sin(ωt) = 1 ― когда маятник находится в крайних положениях, т. е. когда его смещение равно амплитуде.
График колебаний потенциальной энергии пружинного маятника:
Eк ― кинетическая энергия тела, [Дж];
v ― скорость движения тела, [м/с].
У тела, которое совершает колебательные движения, скорость ― переменная величина.
Eк ― кинетическая энергия маятника, [Дж];
ω ― циклическая частота [рад/с];
EКmax ― максимальная кинетическая энергия маятника, [Дж];
ω ― циклическая частота [рад/с].
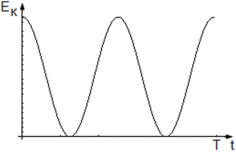
Максимальная кинетическая энергия маятника достигается тогда, когда cos2(ωt) = 1 ― маятник проходит положение равновесия, и она равна нулю, когда маятник находится в крайнем положении.
График колебаний кинетической энергии маятника:
Математический маятник ― это колебательная система, состоящая из материальной точки, подвешенной на нерастяжимой нити или стержне.
l ― длина нити математического маятника [м];
g ― ускорение свободного падения [м/с2].
Существует особый тип колебаний ― вынужденные колебания. Вынужденные колебания происходят только под постоянным периодическим внешним воздействием и их характеристики зависят от характеристик этого воздействия.
Если частота внешнего воздействия, которое вызывает вынужденные колебания, совпадает с собственной внутренней частотой колебательной системы ― возникает явление резонанса. При резонансе резко возрастает амплитуда колебаний системы. Частота, при которой возникает явление резонанса, называется резонансной частотой.
На рисунке показан график резонансной кривой ― увеличение амплитуды при совпадении частоты внешнего воздействия с внутренней частотой системы.




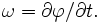
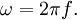
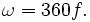
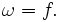



 Читать 0 мин.
Читать 0 мин.