корреляция с клиническими лабораторными данными что это необходима
Что такое клиническая корреляция
Клиническая корреляция – это лечебный процесс, который используют врачи, чтобы помочь себе поставить диагноз пациенту для его правильного лечения или определения его состояния.
Клиническая корреляция используется после диагностического теста – например, после рентгена, биопсии или МРТ – показывает что-то на картине или ткани сканирования все ли нормально или нет. Врач также берет во внимание возраст пациента, истории болезней, физическое здоровье, клинические испытания и симптомы, чтобы определить диагноз, основанный на корреляции (сравнение и сопоставление) клинических результатов пациента.
Примеры клинической корреляции
Следующий пример клинической корреляции поможет вам лучше понять его. Как уже упоминалось выше, она производится для сравнения всей информации, чтобы определить диагноз. Итак, клиническая корреляция, что это?
Например, ваши лимфатические узлы причиняют вам боль, вы идете к врачу для проверки, он же отправляет вас к рентгенологу. Радиолог рассматривает полученный результат и замечает проблему под названием лимфаденит. Он возникает, когда лимфатические железы становятся увеличенными из-за вирусов, бактерий, грибков или по другим причинам.
В худшем случае, воспаленные железы иногда находятся рядом с местом опухоли или инфекции, и увеличение лимфатических узлов является предупредительным знаком для аутоиммунных заболеваний, лимфомы и рака.
Невозможно сразу определить что это, лимфаденит или более тяжелые заболевания, рентгенолог заказывает клиническую корреляцию. Для этого, радиолог отправляет информацию обратно к вашему врачу, который затем будет применять все свои медицинские знания, беря вашу медицинскую историю и сравнивая всю вашу общую картину здоровья на данный момент и симптомы, чтобы определить, насколько серьезна проблема.
Когда в отчете врач пишет, что лимфатические узлы не слишком увеличены и это может быть просто возможно незначительная инфекция, то он берет вас на 6-8 недель наблюдения, чтобы убедиться, как улучшить ваши симптомы, точнее избавить от них, используя разные антибиотики для борьбы с инфекцией.
| Как менопауза влияет на мозг Менопауза может вызвать изменения в вашем мозгу. Узнайте точно, что именно происходит, и что вы можете с этим поделать |
| Что можно сделать с очень сухими волосами Советы по уходу за очень сухими волосами. Какие шампуни для очень сухих волос использовать, причины, чем полоскать, масла для сухих волос и многое другое. |
Если опухоль увеличивается и ваши лимфатические узлы становятся большими, врач исключает инфекцию и делает биопсию, чтобы определить, есть ли у вас аутоиммунное заболевание. В конечном результате, врач сопоставит все данные, чтобы поставить диагноз и назначить правильное лечение.
Корреляция и регрессия
Когда вы исследуете закономерности в своих данных, как вы можете определить, насколько тесно связаны между собой две переменные? Можете ли вы использовать одну переменную для предсказания другой?
В этом модуле вы познакомитесь с концепциями корреляции и регрессии, которые могут помочь вам в дальнейшем изучении, понимании и обмене данными.
Цели
По завершении этого модуля вы сможете:
Раздел 1. Корреляция
В этом модуле вы познакомитесь с двумя концепциями, которые помогут вам в изучении взаимосвязей между переменными: корреляция и регрессия. Начнем с корреляции.
Что такое корреляция?
Корреляция – это техника, которая может показать, насколько сильно связаны пары количественных переменных. Например, количество ежедневно потребляемых калорий и масса тела взаимосвязаны, но эта связь не абсолютная.
Многие из нас знают кого-то, кто очень худой, несмотря на то, что он/она регулярно потребляет большое количество калорий, и мы также знаем кого-то, у кого есть проблемы с лишним весом, даже когда он/она сидит на диете с пониженным содержанием калорий.
Однако средний вес людей, потребляющих 2000 калорий в день, будет меньшим, чем средний вес людей, потребляющих 2500, а их средний вес будет еще меньше, чем у людей, потребляющих 3000, и так далее.
Корреляция может сказать вам, насколько тесно разница в весе людей связана с количеством потребляемых калорий.
Корреляция между весом и потреблением калорий – это простой пример, но иногда данные, с которыми вы работаете, могут содержать корреляции, которых вы никак не ожидаете. А иногда вы можете подозревать корреляции, не зная, какие из них самые сильные. Корреляционный анализ помогает лучше понять связи в ваших данных.
Диаграммы разброса или Точечные диаграммы используются для графического представления взаимосвязей между количественными показателями. Диаграмма показывает данные и позволяет нам проверить свои предположения, прежде чем устанавливать корреляции. Глядя на взаимосвязь между продажами и маркетингом, можно предположить наличие в них корреляции. По мере того, как одна переменная растет, другая, похоже, тоже увеличивается.
Диаграмма, указывающая на корреляцию между двумя количественными переменными
Корреляция против причинно-следственной связи
Теперь вы знаете, как определяется корреляция и как ее можно представить графически. Теперь давайте посмотрим, как понимать корреляцию.
Во-первых, важно понимать, что корреляция никогда не доказывает наличие причинно-следственной связи.
Корреляция говорит нам только о том, насколько сильно пара количественных переменных линейно связана. Она не объясняет, как и почему.
Например, продажи кондиционеров коррелируют с продажами солнцезащитных кремов. Люди покупают кондиционеры, потому что они купили солнцезащитный крем, или наоборот? Нет. Причина обеих покупок явно в чем-то другом, в данном случае – в жаркой погоде.
Измерение корреляции
Корреляция Пирсона, также называемая коэффициентом корреляции, используется для измерения силы и направления (положительного или отрицательного) линейной связи между двумя количественными переменными. Когда корреляция измеряется в выборке данных, используется буква r. Критерий Пирсона r может находиться в диапазоне от –1 до 1.
Когда r = 1, существует идеальная положительная линейная связь между переменными, это означает, что обе переменные идеально коррелируют с увеличением значений. Когда r = –1, существует идеальная отрицательная линейная связь между переменными, это означает, что обе переменные идеально коррелируют при уменьшении значений. Когда r = 0, линейная связь между переменными не наблюдается.
На графиках разброса ниже показаны корреляции, где r = 1, r = –1 и r = 0.
Переверните каждую карту ниже, чтобы увидеть значение для этой совокупности.
Идеальная положительная корреляция
Когда r = 1, есть идеальная положительная линейная связь между переменными, и это означает, что обе переменные идеально коррелируют с увеличением значений.
Идеальная отрицательная корреляция
Когда r = –1, существует идеальная отрицательная линейная связь между переменными, и это означает, что обе переменные идеально коррелируют при уменьшении значений.
Нет линейной корреляции
Когда r = 0, линейная зависимость между переменными не наблюдается.
С реальными данными вы никогда не увидите значений r «–1», «0» или «1».
Как правило, чем ближе r к 1 или –1, тем сильнее корреляция, это показано в следующей таблице.
Сила корреляции
Очень сильная корреляция
Очень слабая корреляция или ее нет вообще
Условие корреляции
Чтобы корреляции были значимыми, они должны использовать количественные переменные, и описывать линейные отношения, при этом не может быть выбросов.
В 1973 году статистик по имени Фрэнсис Анскомб разработал показатель «квартет Анскомба», он показывает важность визуального представления данных в виде графиков, а не простого выполнения статистических тестов.
Выделенный график разброса в верхнем левом углу – единственный, который удовлетворяет условиям корреляции.
Четыре визуализации в его квартете показывают одну и ту же линию тренда, поэтому значение r будет одинаковым для всех четырех.
Что вы заметили? Только один из графиков рассеяния соответствует критериям линейности и отсутствия выбросов.
Другими словами, мы не должны проводить корреляции на трех из четырех примерах, потому что не имеет смысла устанавливать сильные отношения.
Проверка знаний
Силу корреляции при значении r, равному –0,52, лучше всего можно описать как:
Резюме
Итак, вы ознакомились с концепциями статистической техники корреляции. На следующем уроке вы узнаете о линейной регрессии.
Раздел 2. Линейная регрессия
На предыдущем уроке вы узнали, что корреляция относится к направлению (положительному или отрицательному) и силе связи (от очень сильной до очень слабой) между двумя количественными переменными.
Линейная регрессия также показывает направление и силу взаимосвязи между двумя числовыми переменными, но регрессия использует наиболее подходящую прямую линию, проходящую через точки на диаграмме рассеяния, чтобы предсказать, как X вызывает изменение Y. При корреляции значения X и Y взаимозаменяемы. При регрессии результаты анализа изменятся, если поменять местами X и Y.
Диаграмма рассеяния с линией регрессии
Линия регрессии
Как и в случае с корреляциями, для того, чтобы регрессии были значимыми, они должны:
Как и корреляция, линейная регрессия отображается на диаграмме рассеяния
Линия регрессии на диаграмме рассеяния – это наиболее подходящая прямая линия, которая проходит через точки на диаграмме рассеяния. Другими словами, это линия, которая проходит через точки с наименьшим расстоянием от каждой из них до линии (поэтому в некоторых учебниках вы можете встретить название «регрессия наименьших квадратов»).
Почему эта линия так полезна? Мы можем использовать вычисление линейной регрессии для вычисления или прогнозирования нашего значения Y, если у нас есть известное значение X.
Чтобы было понятнее, давайте рассмотрим пример.
Пример регрессии
Представьте, что вы хотите предсказать, сколько вам нужно будет заплатить, чтобы купить дом площадью 1,500 квадратных футов.
Давайте используем для этого линейную регрессию.
Вот диаграмма рассеяния, показывающая цены на жилье (ось Y) и площадь в квадратных футах (ось x).
Вы можете видеть, что дома с большим количеством квадратных футов, как правило, стоят дороже, но сколько именно вам придется потратить на дом размером 1500 квадратных футов?
Диаграмма рассеяния цен на дома и квадратных метров
Чтобы помочь вам ответить на этот вопрос, проведите линию через точки. Это и будет линия регрессии. Линия регрессии поможет вам предсказать, сколько будет стоить типовой дом определенной площади в квадратных метрах. В этом примере вы можете видеть уравнение для линии регрессии.
Уравнение линии регрессии
Уравнение линии регрессии: Y = 113x + 98,653 (с округлением).
Что означает это уравнение? Если вы купили просто место без площади (пустой участок), цена составит 98,653 доллара. Вот как можно решить это уравнение:
Чтобы найти Y, умножьте значение X на 113, а затем добавьте 98,653. В этом случае мы не смотрим на квадратные метры, поэтому значение X равно «0».
Значение 98,653 называется точкой пересечения по оси Y, потому что здесь линия пересекает ось Y. Это – значение Y, когда X равно «0».
Но что такое 113? Число «113» – это наклон линии. Наклон – это число, которое описывает как направление, так и крутизну линии. В этом случае наклон говорит нам, что за каждый квадратный фут цена дома будет расти на 113 долларов.
Итак, сколько вам нужно будет потратить на дом площадью 1500 квадратных футов?
Взгляните еще раз на эту диаграмму рассеяния. Синие отметки – это фактические данные. Вы можете видеть, что у вас есть данные для домов площадью от 1100 до 2450 квадратных футов.
Насколько можно быть уверенным в результате, используя приведенное выше уравнение, чтобы спрогнозировать цену дома площадью в 500 квадратных футов? Насколько можно быть уверенным в результате, используя приведенное выше уравнение, чтобы предсказать цену дома площадью 10,000 квадратных футов?
Поскольку оба этих измерения находятся за пределами диапазона фактических данных, вам следует быть осторожными при прогнозировании этих значений.
Величина достоверности аппроксимации
Наведите курсор на линию регрессии, чтобы увидеть значение величины достоверности аппроксимации r.
В дополнение к уравнению в этом примере мы также видим значение величины достоверности аппроксимации r (также известная как коэффициент детерминации).
Это значение является статистической мерой того, насколько близки данные к линии регрессии или насколько хорошо модель соответствует вашим наблюдениям. Если данные находятся точно на линии, значение величины достоверности аппроксимации будет 1 или 100%, и это означает, что ваша модель идеально подходит (все наблюдаемые точки данных находятся на линии).
Для наших данных о ценах на жилье значение величины достоверности аппроксимации составляет 0,70, или 70%.
Корреляция против причинно-следственной связи
Теперь давайте рассмотрим, как отличить линейную регрессию от корреляции.
Линейная регрессия
Корреляция
Готовы проверить свои знания? В следующем упражнении определите, чему соответствует каждое из описаний: корреляции или регрессии.
Варианты для категорий: «корреляция» или «регрессия».
Измеряется величиной достоверности аппроксимации
Прогнозирует значения Y на основе значений X.
Не предсказывает значения Y из значений X, только показывает взаимосвязь.
Переменные оси X и Y взаимозаменяемы.
Если поменять местами X и Y, результаты анализа изменятся.
Резюме
Итак, здесь вы познакомились со статистическими концепциями корреляции и регрессии. Это поможет вам лучше исследовать и понимать данные, с которыми вы работаете, путем изучения взаимосвязей в них.
Что такое корреляция акций и облигаций?
Объясните, пожалуйста, простым языком, что такое корреляция ценных бумаг? Почему о ней говорят при составлении портфеля и что значит, когда она отрицательная?
Корреляция показывает, насколько активы схожи по поведению. Показатель описывает закономерности. Например, если при росте одного актива другой дешевеет и эта закономерность подтверждается историческими данными, говорят, что у активов обратная корреляция. Это относится как к отдельным ценным бумагам, так и к широким рынкам, классам активов и секторам экономики.
Коэффициент корреляции вычисляется на конкретном историческом отрезке. Он обозначается буквой r и принимает значения от −1 до +1. Если два актива движутся в связке, то коэффициент корреляции будет ближе к +1, а если в противоположных направлениях — ближе к −1. Но когда корреляция близка к нулю, взаимосвязи между ними нет. Это значит, что при росте или падении одного актива другой может вообще никак себя не проявлять. Например, корреляция акций и облигаций на рынке США в период с 1950 по 2012 год составила 0,11.
Расскажу, как можно использовать знание о корреляции при формировании портфеля.
Роль корреляции в управлении портфелем
Понимание корреляции между инструментами позволяет диверсифицировать портфель и снизить инвестиционные риски.
Например, если инвестор собрал портфель из 10 нефтегазовых компаний, он защитил себя только от специфических рисков, связанных с конкретным эмитентом. Волатильность портфеля по-прежнему будет высокой: если цены на нефть упадут, портфель также уйдет в красную зону из-за тесной корреляции акций.
Чтобы диверсификация работала, необходимо использовать инструменты с низкой или обратной корреляцией. Тогда движение цены одного актива будет компенсироваться движением другого. Так, государственные облигации — наиболее частный диверсификатор для акций, поскольку у этих активов исторически низкая взаимосвязь друг с другом.
Таким же образом устроен и механизм хеджирования, когда инвестор открывает позицию с отрицательной корреляцией к исходному активу, чтобы застраховаться от его падения. Например, так называемые обратные ETF обладают корреляцией, близкой к −1 по отношению к исходному активу.
Как победить выгорание
Как изменяется корреляция со временем
Современная теория портфеля позволяет найти идеальную смесь активов, при которой у портфеля будет оптимальное соотношение доходности и риска. Но главный недостаток этой теории в том, что корреляции со временем могут меняться. Два актива могут начать двигаться синхронно, даже если в прошлом их взаимосвязь была низкой. И заметить это можно только постфактум — на исторических данных.
Например, компания Blackstone провела исследование корреляции между разными классами активов за 20 лет. Результаты показали, что корреляция со временем только увеличивается. Это связано с разными факторами: тесной интеграцией экономик, глобальными производственными цепочками и усилившимся влиянием рынков друг на друга.
Seeking an Alternative — BlackstonePDF, 421 КБ
Если посмотреть на десятилетие перед кризисом 2008 года, то корреляция большинства инструментов по отношению к S&P 500 была ниже 0,5. Но после 2008 года она заметно выросла. Теперь только у высоконадежных облигаций по-прежнему слабая связь с акциями, хотя их корреляция сменилась с отрицательной на положительную: если раньше при падении S&P 500 они росли, то теперь тоже падают, пусть и не так сильно.
Корреляция различных классов активов с индексом S&P 500
| 1998—2007 | 2008—2020 | |
|---|---|---|
| Глобальные акции | 0,84 | 0,89 |
| Недвижимость | 0,32 | 0,74 |
| Высокодоходные облигации | 0,49 | 0,73 |
| Товары | −0,01 | 0,59 |
| Высоконадежные облигации | −0,21 | 0,01 |
Корреляция и волатильность
Между корреляцией и волатильностью существует взаимосвязь: когда рынки становятся волатильными, корреляции между инструментами возрастают. Поэтому рост корреляции со временем можно объяснить тем, что за последние десятилетия рынки стали более волатильными. Например, с 2000 по 2009 год было 95 торговых сессий, когда S&P 500 сдвинулся на 3% и больше. А за предшествующие 50 лет был всего 81 случай.
Количество дней в каждом десятилетии, когда S&P 500 сдвинулся на 3% и более
| 1950—1959 | 5 |
| 1960—1969 | 9 |
| 1970—1979 | 16 |
| 1980—1989 | 24 |
| 1990—1999 | 27 |
| 2000—2009 | 95 |
| 2010—2019 | 50 |
Особенно явно корреляции усиливаются во время фондовых обвалов. В панике инвесторы массово скидывают ценные бумаги широкого спектра, и в итоге все падает независимо от корреляции.
Поэтому на спокойном рынке с 2014 по 2017 год положительно коррелировали между собой только высокорисковые активы: S&P 500, глобальные акции, бумаги развивающихся рынков и фонды REIT. А низкорисковые активы были связаны только между собой. Это, например, муниципальные, корпоративные облигации, долгосрочные трежерис. При этом корреляции между этими двумя группами активов практически не наблюдалось.
Но во время коронавирусного кризиса корреляции усилились. Все перечисленные выше активы стали взаимосвязаны. А облигации, которые традиционно считаются защитным инструментом, падали вместе с рисковыми активами.
Как посчитать корреляцию
Чтобы рассчитать корреляцию, можно воспользоваться онлайн-калькулятором, например от Portfolio Visualizer или более простым вариантом от Unicornbay.
Я использовал Portfolio Visualizer, чтобы проверить корреляции между такими классами активов:
Для этого я вбил через пробелы указанные тикеры, выбрал расчет корреляций на основе месячной доходности инструментов и рассчитал 36-месячную скользящую.
Корреляции рассчитывались в рамках окна шириной три года, которое двигалось по шкале времени с марта 2006 по февраль 2021 года. Скользящая корреляция за 36 месяцев позволяет увидеть, как менялись ее значения с течением времени.
Я начал расчет с марта 2006 года, так как для фонда DBC более ранних данных нет.
Результаты расчетов представлены в таблице. Мы видим, что исторически у недвижимости, коммодити и S&P 500 слабая отрицательная корреляция по отношению к долгосрочным и коротким облигациям.
36-месячная скользящая корреляция разных классов активов
| Название | Тикер | TLT | SHY | SPY | GLD | DBC | VNQ |
|---|---|---|---|---|---|---|---|
| iShares 20+ Year Treasury Bond ETF | TLT | — | 0,54 | −0,32 | 0,23 | −0,37 | −0,01 |
| iShares 1-3 Year Treasury Bond ETF | SHY | 0,54 | — | −0,37 | 0,29 | −0,21 | −0,18 |
| SPDR S&P 500 ETF Trust | SPY | −0,32 | −0,37 | — | 0,05 | 0,54 | 0,72 |
| SPDR Gold Shares | GLD | 0,23 | 0,29 | 0,05 | — | 0,36 | 0,09 |
| Invesco DB Commodity Tracking | DBC | −0,37 | −0,21 | 0,54 | 0,36 | — | 0,34 |
| Vanguard Real Estate ETF | VNQ | −0,01 | −0,18 | 0,72 | 0,09 | 0,34 | — |
Как рассчитать корреляцию в «Экселе»
Скользящие корреляции также достаточно легко рассчитать в «Экселе». В этом помогает функция КОРРЕЛ() — или CORREL() в англоязычной версии.
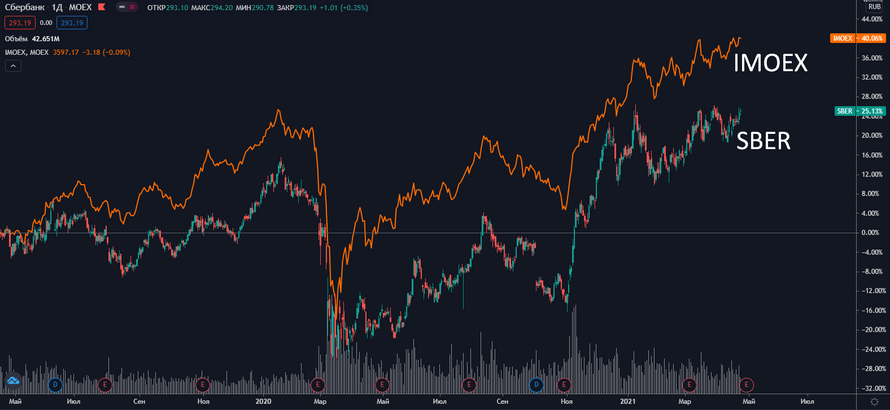
Для начала необходимо сформировать два массива данных с котировками интересующих инструментов. Для примера я возьму акции «Газпрома» (GAZP) и Сбербанка (SBER) и выгружу цены бумаг на конец каждого месяца с 1 марта 2015 по 1 марта 2021 года. Всего получилось 73 месяца.
После этого можно воспользоваться функцией КОРРЕЛ(), чтобы посчитать скользящие корреляции. Я приведу пример, как рассчитать скользящую трехмесячную, то есть значение за каждое предыдущее окно в три месяца.
Что в итоге
Корреляция показывает схожесть поведения активов. Понимание корреляций активов используется при диверсификации, а также оптимизации стратегии согласно современной теории портфеля.
Корреляция рассчитывается на конкретном временном отрезке, и она может меняться. Как показывают исторические данные, с течением времени корреляция растет.
Корреляция усиливается на падающих рынках и вместе с увеличением волатильности.
Что делать? Читатели спрашивают — эксперты Т—Ж отвечают
MarketTwits, как-то неправильно приводить в пример корреляцию акции и индекса, состоящего на 1/6 из этих акций. Вот Русгидро и Сбер сравнить да, выбрать их индекса максимально отрицательно коррелирующие и составить свой идеальный индекс)