координатная плоскость xoy что это

Координатная плоскость xoy что это

то вектор нормали коллинеарен вектору k = (0, 0, 1). Поэтому плоскость перпендикулярна оси OZ, а значит параллельна плоскости XOY. Координатная плоскость XOY имеет уравнение z = 0.

Аналогично, x = 0 — уравнение координатной плоскости YOZ; x = а — уравнение плоскости, параллельной YOZ; y = 0 — уравнение плоскости XOZ; y = b — уравнение плоскости, параллельной XOZ.

Если равна нулю только одна из координат вектора нормали, то нормаль перпендикулярна, а плоскость, следовательно, параллельна соответствующей оси. Например, плоскость Ax + Cz + D = 0 параллельна оси OY (возможно, содержит эту ось).

Вопросы о взаимном расположении плоскостей решаются с помощью вектора нормали. Пусть две плоскости заданы своими уравнениями: A1x + B1y + C1z + D1 = 0 (плоскость P1), A2x + B2y + C2z + D2 = 0 (плоскость P2).

Запишем в краткой, символической форме условия параллельности и перпендикулярности плоскостей:

Угол между плоскостями равен углу между векторами нормали и находится с помощью скалярного произведения (см. раздел 4.2).

Пример 9. Найти угол между плоскостями 2x — 2y + z — 5 = 0, x — z + 7 = 0.

Решение. Найдём косинус угла между векторами нормали N1 = (2, —2, 1) и N2 = (1, 0, —1):

Используя таблицы или калькулятор, можно найти.

Как известно, через любые 3 точки, не лежащие на одной прямой, можно провести единственную плоскость. Научимся решать эту важную задачу в общем виде, а затем рассмотрим пример.

Пусть точки M1(x1, y1,z1), M2(x2,y2,z2), M3(x3,y3,z3) не лежат на одной прямой. Мы помним, что главное для записи уравнения плоскости — найти вектор нормали, т. е. какой-нибудь вектор, перпендикулярный плоскости. В качестве такого вектора можно взять векторное произведение:

Источник

1.2.2. Общее уравнение плоскости. Неполное уравнение

Раскрывая скобки и обозначая свободный член – Ax0 – By0 – Cz0 = D, получим общее уравнение плоскости В пространстве R3:

Ax+By+Cz+D=0, A2+B2+C2>0. (4)

Итак, линейное относительно текущих координат x, y,z уравнение (4) определяет плоскость в пространстве (причем, =(A, B,C) ее нормаль). Можно показать, что верно и обратное утверждение: всякое линейное уравнение (4) в пространстве R3 определяет некоторую плоскость.

Пример. Написать уравнения координатных плоскостей.

Для того, чтобы написать уравнение любой плоскости надо знать координаты какой-нибудь точки на плоскости и какой-нибудь вектор, перпендикулярный плоскости.

В нашем примере все координатные плоскости проходят через точку M0(0,0,0) – начало координат.

А в качестве нормалей к координатным плоскостям можно взять соответственно базисные векторы .

Плоскость XOY: М0(0,0,0), (0,0,1)=(A, B,C).

0(x – 0) + 0(y – 0) + 1(z – 0)=0

Уравнение плоскости XOY: z=0.

Плоскость YOZ: M0(0,0,0), :

Уравнение плоскости YOZ: x=0.

Плоскость XOZ: M0(0,0,0), :

Уравнение плоскости XOZ: y=0.

Заметим, что в нашем примере в уравнениях координатных плоскостей отсутствуют два члена с текущими координатами (какие-либо два из коэффициентов A, B,C равны нулю).

Уравнение плоскости (4), в котором хотя бы один из коэффициентов A, B,C или D равен нулю, называют Неполным уравнением плоскости. В этих случаях плоскость либо параллельна одной из координатных осей (один из коэффициентов A, B,C равен нулю, или, что то же, вектор нормали ортогонален одной из координатных осей); либо плоскость (4) параллельна одной из координатных плоскостей (два из коэффициентов A, B,C равны нулю, параллелен какой-нибудь координатной оси); если же коэффициент D уравнения (4) равен нулю, т. е. точка (0,0,0) удовлетворяет уравнению плоскости, плоскость проходит через начало координат.

Источник

Общее уравнение плоскости

В данной статье мы рассмотрим общее уравнение плоскости в пространстве. Определим понятия полного и неполного уравнения плоскости. Для построения общего уравнения плоскости пользуйтесь калькулятором уравнение плоскости онлайн.

Пусть задана произвольная декартова прямоугольная система координат Oxyz. Общим уравнением плоскости называется линейное уравнение вида:

Мы покажем, что линейное уравнение (1) в пространстве определяет плоскость и любой плоскость в пространстве можно представить линейным уравнением (1). Докажем следующую теорему.

Теорема 1. В произвольной декартовой прямоугольной системе координат в пространстве каждая плоскость α может быть задана линейным уравнением (1). Обратно, каждое линейное уравнение (1) в произвольной декартовой прямоугольной системе координат в пространстве определяет плоскость.

Доказательство. Достаточно доказать, что плоскость α определяется линейным уравнением при какой нибудь одной декартовой прямоугольной системе координат, поскольку тогда она будет определяться линейным уравнением и при любом выборе декартовой прямоугольной системы координат.

Пусть в пространстве задана плоскость α. Выберем оси Ox и Oy так, чтобы они располагались на плоскости α, а ось Oz направим перпендикулярно к этой плоскости. Тогда линейное уравнение z=0 будет уравнением плоскости, т.к. координаты любой точки, принадлежащей этой плоскости удовлетворяют уравнению z=0, а координаты любой точки, не лежащей на этой плоскости − нет. Первая часть теоремы доказана.

Таким образом, существует точка M₀(x₀, y₀, z₀), координаты которой удовлетворяют уравнению (1):

Вычитая из уравнения (1) тождество (2), получим

которая эквивалентна уравнению (1).

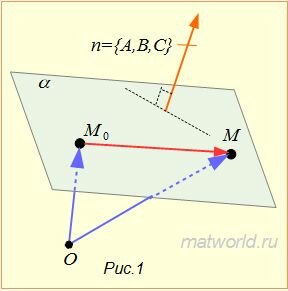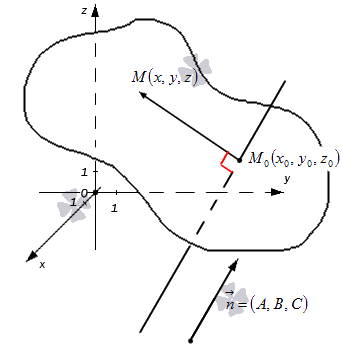
Покажем, что (3) определяет некоторую плоскость, проходящую через точку M₀(x₀, y₀, z₀) и перпендикулярную вектору n=<A,B,C> (n≠0, так как хотя бы один из чисел A,B,C отлично от нуля).

Если точка M₀(x₀, y₀, z₀) принадлежит плоскости α, то ее координаты удовлетворяют уравнению (3), т.к. векторы n=<A,B,C> и перпендикулярны (Рис.1) и их скалярное произведение равно нулю:

.

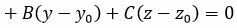Если же точка M(x, y, z) не лежит на плоскости α, то векторы n=<A,B,C> и не ортогональны. Тогда их скалярное произведение не равно нулю, т.е. координаты точки M(x, y, z) не удовлетворяют условию (3). Теорема доказана.

Одновременно с доказательством теоремы 1 мы получили следующее утверждение.

Утверждение 1. В декартовой прямоугольной системе координат вектор с компонентами (A,B,C) перпендикулярен плоскости Ax+By+Cz+D=0.

Утверждение 2. Если два общих уравнения плоскости

определяют одну и ту же плоскость, то найдется такое число λ, что выпонены равенства

Умножая уравнение (7) на λ и вычитая из него уравнение (8) получим:

Так как выполнены первые три равенства из выражений (6), то D₁λ−D₂=0. Т.е. D₂=D₁λ. Утверждение доказано.

Неполные уравнения плоскости

Рассмотрим все возможные варианты неполных уравнений плоскости:

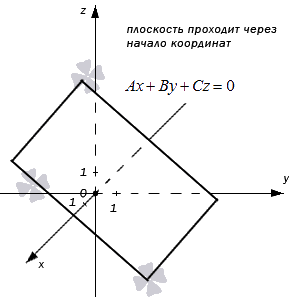
При D=0, имеем уравнение плоскости Ax+By+Cz=0, проходящей через начало координат (Рис.2). Действительно, точка O(0,0,0) удовлетворяет этой системы линейных уравнений.

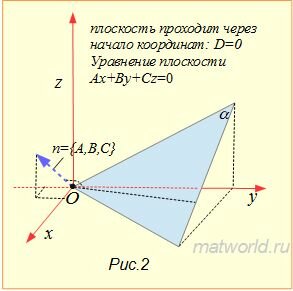
При A=0, имеем уравнение плоскости By+Cz+D=0, которая параллельна оси Ox (Рис.3). В этом случае нормальный вектор плоскости n=<0,B,C> лежит на координатной плоскости Oyz.

При B=0, имеем уравнение плоскости Ax+Cz+D=0, которая параллельна оси Oy (Рис.4).

При C=0, имеем уравнение плоскости Ax+By+D=0, которая параллельна оси Oz (Рис.5).

При A=0,B=0 имеем уравнение плоскости Cz+D=0, которая параллельна координатной плоскости Oxy (Рис.6).

При B=0,C=0 имеем уравнение плоскости Ax+D=0, которая параллельна координатной плоскости Oyz (Рис.7).

При A=0,C=0 имеем уравнение плоскости By+D=0, которая параллельна координатной плоскости Oxz (Рис.8).

При A=0,B=0,D=0 имеем уравнение плоскости Cz=0, которая совпадает с координатной плоскостью Oxy (Рис.9).

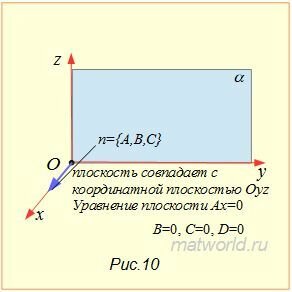
При B=0,C=0,D=0 имеем уравнение плоскости Ax=0, которая совпадает с координатной плоскостью Oyz (Рис.10).

При A=0,C=0,D=0 имеем уравнение плоскости By=0, которая совпадает с координатной плоскостью Oxz (Рис.11).

Рассмотрим примеры построения общего уравнения плоскости.

Пример 1. Построить общее уравнение плоскости, проходящей через точку M(4,−1,2) параллельной координатной плоскости Oxy.

Решение. Общее уравнение плоскости, проходящей через некоторую точку M(x₀,y₀,z₀) имеет вид (3). Подставляя координаты точки M в (3), получим:

Так как плоскость параллельна координатной плоскости Oxy, то направляющий вектор имеет следующий вид n=<A,B,C>=<0,0,1>, т.е. A=0, B=0, C=1.

Подставляя коэффициенты A,B,C в (9), получим:

Пример 2. Построить общее уравнение плоскости, проходящей через начало координат и имеющий нормальный вектор n==<2,3,1>.

Решение. Начало координат имеет коэффициенты (0,0,0). Общее уравнение плоскости, проходящей через некоторую точку M(x₀,y₀,z₀) имеет вид (3). Подставляя коэффициенты начальной точки в (3), получим:

Так как плоскость имеет нормальный вектор n=<A,B,C>=<2,3,1>, т.е. A=2, B=3, C=1, подставляя коэффициенты A,B,C в (10), получим:

Онлайн калькулятор для построения общего уравнения плоскости находится здесь. Там же вы найдете примеры построения общего уравнения плоскости, если известны три точки этой плоскости или если известна одна точка и нормальный вектор этой плоскости.

Источник

Общее уравнение плоскости : описание, примеры, решение задач

В статье рассмотрим такой тип уравнений плоскости как общее уравнение, получим его вид и разберем на практических примерах. Рассмотрим частные случаи и понятие общего неполного уравнения плоскости.

Общее уравнение плоскости: основные сведения

Также вспомним определение прямой, перпендикулярной к плоскости: прямая является перпендикулярной к заданной плоскости, если она перпендикулярна любой прямой, принадлежащей этой плоскости.

Теорема состоит из двух частей. Разберем доказательство каждой из них.

Уравнение вида A x + B y + C z + D = 0 называют общим уравнением плоскости в прямоугольной системе координат O x y z трехмерного пространства.

Раскроем чуть шире смысл теорем.

Укажем пример как иллюстрацию этих утверждений.

Общее уравнение плоскости, проходящей через точку

Решение

Подставим координаты точки М 0 в исходной уравнение плоскости:

Ответ: точка М 0 принадлежит заданной плоскости; точка N 0 – не принадлежит.

Решение

Разберем обратную задачу, когда требуется составить уравнение плоскости по заданным координатам нормального вектора.

Возможно получить это уравнение другим способом.

Решение

Рассмотрим два способа решения.

Чтобы получить искомое общее уравнение плоскости, необходимо также воспользоваться необходимым и достаточным условием перпендикулярности векторов и тогда:

Неполное общее уравнение плоскости

Разберем все возможные варианты общих неполных уравнений в прямоугольной системе координат трехмерного пространства.

A · 0 + B · 0 + C · 0 = 0 ⇔ 0 ≡ 0

Р​​ешение

Задачу возможно решить еще одним способом.

Решение

Источник

Урок 46 Бесплатно Координатная плоскость

До этого занятия мы обсуждали с вами только прямую и все, что с ней связано.

Сегодня урок посвятим изучению плоскости.

Узнаем, что называют координатной плоскостью и как получить её из обычной плоскости.

Познакомимся с прямоугольной системой координат на плоскости и разберем ее основные характеристики и особенности.

Выясним области применения и использования систем координат в практических целях и в жизни человека.

Научимся пользоваться прямоугольной системой координат на плоскости: определять координаты заданных точек и по заданным координатам точки находить ее положение на координатной плоскости.

Координатная плоскость и ее основные особенности

Представим движение автомобиля по прямолинейному участку дороги.

Любой прямолинейный участок дороги легко представить с помощью координатной прямой.

Координатная прямая позволяет нам связать точки на этой прямой с числом.

Вам уже известно, как из любой прямой получить координатную прямую.

Необходимо на прямой выбрать начало отсчета, задать направление и единичный отрезок (масштаб).

В результате с помощью координатной прямой вы однозначно определите, что конкретной точке на прямой соответствует ее единственное верное значение с соответствующим знаком.

И наоборот, если известна координата точки, то можно определить положение этой точки на координатной прямой.

Таким образом, для указания местоположения точки (в нашем случае автомобиля) на прямой нужна только одна координата на координатной оси.

В жизни часто приходится устанавливать положение точки по нескольким параметрам. В таком случае для однозначного определения положения точки требуется больше информации.

Предположим, купили мы билет на концерт.

Чтобы определить расположение конкретного кресла в зале, в билете указывают адрес места: номер ряда и номер кресла в ряду.

Так как каждому месту ставится в соответствие два числа, то для однозначного определения положения точки нам не будет хватать одной координатной прямой.

Для обозначения числами точного положения точки на плоскости используют математическую модель, которую называют координатной плоскостью.

Чтобы из обычной плоскости получить координатную, необходимо на этой плоскости задать определенную систему координат.

Существует различные системы координат.

Мы рассмотрим прямоугольную систему координат на плоскости.

Прямоугольной системой координат на плоскости называют систему из двух взаимно перпендикулярных прямых с общим началом отсчета и общей масштабной единицей.

Рассмотрим основные составляющие прямоугольной системы координат.

Единичный отрезок выбирается чаще всего одинаковый для каждой координатной оси.

Направление осей указывается стрелкой, каждая ось подписывается буквой.

Для координатных осей обычно выбирают положительное направление, т.е. «по умолчанию» принято использовать правостороннюю систему координат, в которой за положительное направление осей принимают ось ординат, направленную вверх, и ось абсцисс, направленную вправо.

Если приходится по каким-либо причинам использовать левостороннюю прямоугольную систему координат, то данный факт оговаривают в задаче.

Положение точки на плоскости определяется двумя упорядоченными числами: координатами х и y.

Координату точки на плоскости записывают так:

Например, координата точки A:

A(2;-1), где

У меня есть дополнительная информация к этой части урока!

Чтобы запомнить порядок следования абсциссы и ординаты в записи координаты точки, часто используют такое сравнение:

Представьте, многоэтажный дом, а в нем вашу квартиру.

Чтобы попасть домой, первым делом вам необходимо зайти в нужный подъезд (координата по оси Ох), а затем подняться на нужный этаж (координата по оси Оу).

Координаты могут иметь различные числовые значения, в том числе быть равными нулю.

Если ордината точки равна нулю, то точка лежит на оси Ох.

Если абсцисса точки равна нулю, то точка лежит на оси Оу.

Нумерация координатных плоскостей ведется против часовой стрелки римскими цифрами I, II, III, IV.

Если точка имеет положительную координату х (х > 0) и положительную координату у (у > 0), то она лежит в I координатной четверти.

Если точка имеет отрицательную координату х (х 0), то она лежит во II координатной четверти.

Античные ученые, мыслители (астрономы, философы, географы) на протяжении нескольких столетий пытались создать теорию о происхождении окружающего мира и всего мироздания в целом, изобразить известные им моря, океаны, страны в чертежах, а звездное небо на карте.

Благодаря великим умам появилось огромное множество фундаментальных знаний, понятий, представлений.

Появилось представление о Земле как о шаре, о ее расположение на звездном небе; создавались все более совершенные карты и планы, методы определения географических координат; на карту наносились линии широты и долготы, сетка параллелей и меридиан.

Долгое время лишь география и астрономия пользовались данными знаниями.

В XIV веке французский философ, астроном, математик Никола Орем пытался применить метод координат к геометрии.

Одной из самых важных математических работ Орема стал «Трактат о конфигурации качеств».

Именно в этой работе он ввел графическое изображение зависимости одной величины от другой с помощью прямоугольной системы координат, называя широтой и долготой то, что сейчас называют абсциссой и ординатой.

Это нововведение стало отправной точкой создания современного метода координат.

Научному обоснованию прямоугольной системы координат мы обязаны французскому ученому, философу Рене Декарту.

Он обобщил известные на то время знания по этой теме и дал научное истолкование прямоугольной системе координат.

Предложенная им прямоугольная система координат получила его имя, ее стали называть декартовой системой координат.

Координатный метод описания геометрических объектов положил начало аналитической геометрии.

Создание аналитической геометрии позволило переводить геометрические свойства тел и кривых на алгебраический язык, вместо геометрических построений использовать расчеты; кроме того, стало возможным анализировать геометрические объекты с помощью уравнений.

Развитием координатного метода и аналитической геометрии занимался также современник Рене Декарта, знаменитый французский ученый Пьер Ферма.

Однако все научные труды Ферма были опубликованы только после его смерти

Пройти тест и получить оценку можно после входа или регистрации

Источник