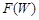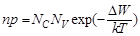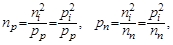концентрация носителей заряда в чем измеряется

Концентрация носителей заряда в чем измеряется

Так как число свободных носителей заряда в полупроводнике постоянно при данной температуре и числа электронов и дырок при собственной электропроводности равны между собой, то для любого полупроводника, находящегося в равновесном состоянии, можно записать: .

В полупроводниках с примесной электропроводностью концентрация электронов донорной примеси значительно превышает собственную концентрацию в довольно широком интервале температур. Поэтому можно считать, что концентрация электронов полностью определяется концентрацией донорной примеси . Тогда концентрация дырок, являющихся неосновными носителями заряда, в полупроводнике n-типа . Так как и «да да , то при увеличении температуры концентрации неосновных носителей заряда увеличивается по экспоненциальному закону. Аналогичное выражение имеет место и для полупроводника p-типа.

Из приведенных уравнений следует, что увеличение количества электронов при данной температуре всегда вызывает пропорциональное уменьшение количества дырок, и наоборот.

Так как при данной температуре количество электронов и дырок постоянно, то рекомбинация одной пары вызовет генерацию электрона и дырки в другом месте. Рекомбинация и генерация дырок и электронов в полупроводнике происходят непрерывно.

В зависимости от характера процессов различают несколько видов рекомбинаций: межзонная; через рекомбинационные центры; поверхностная.

При межзонной рекомбинации электроны из зоны проводимости непосредственно переходят в валентную зону (рис. 2.4, а, б). При этом выделяется энергия, равная ширине запрещенной зоны: . Эта энергия выделяется или в виде фотона (излучательная рекомбинация), или в виде фонона (безызлучательная рекомбинация). Характер излучения зависит от строения зон полупроводника. Если экстремумы зон совпадают (рис. 2.4, а) (в реальном полупроводнике ширина запрещенной зоны меняется в зависимости от геометрической координаты) и при переходе электрона значение его импульса остается постоянным, то энергия выделяется в виде фотона.

При несовпадении экстремумов (рис. ) обычно имеет место безызлучательная рекомбинация с выделением фонона.

В большинстве полупроводников, используемых в настоящее время, рекомбинация осуществляется через рекомбинационные центры, которые называют рекомбинационными ловушками или просто ловушками. Ловушки — это атомы примесей или дефекты кристаллической структуры, энергетические уровни которых находятся в запрещенной зоне, как правило, достаточно далеко как от валентной зоны, так и от зоны проводимости. Электрон из зоны проводимости может перейти на энергетический уровень ловушки (переход ), затем либо вернуться назад (переход 2), либо перейти в валентную зону (переход 3) (рис. 2.4, в). В последнем случае произойдет восстановление валентной связи. Рекомбинация носит своеобразный ступенчатый характер, и энергия АЕ выделяется двумя порциями. Аналогичным двухступенчатым путем может происходить и генерация зарядов.

Поверхностная рекомбинация обусловлена тем, что на поверхности кристалла в результате ее окисления, адсорбции атомов примесей, наличия дефектов кристаллической решетки, вызванных механической обработкой, появляются поверхностные состояния, энергетические уровни которых лежат в запрещенной зоне.

Источник

Определение концентрации и подвижности основных носителей заряда по измерениям эффекта Холла

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное
учреждение высшего профессионального образования
«Новгородский государственный университет
имени Ярослава Мудрого»

Кафедра «Общей и экспериментальной физики»

Определение концентрации и подвижности основных носителей заряда по измерениям эффекта Холла

Лабораторная работа по учебной дисциплине

» Методы исследования материалов и структур электроники «

Великий Новгород

Ознакомиться с эффектом Холла и с его помощью определить концентрацию, подвижность и удельную проводимость образца полупроводникового материала.

Эффект был открыт американским физиком Эдвином Холлом в 1879 году в тонких пластинках золота. Холл обнаружил следующее явление: если металлическую пластинку, вдоль которой течёт постоянный электрический ток, поместить в перпендикулярное к ней магнитное поле, то наблюдается возникновение поперечной разности потенциалов, называемой ЭДС Холла.

Эффекту можно дать изложенное ниже объяснение.

Рис. 1 Появление поверхностных зарядов и холловской напряженности электрического поля в акцепторном полупроводнике

Рассмотрим для примера акцепторный полупроводник. Удельная электропроводность полупроводника с примесной проводимостью определяется формулой:

,

где – элементарный заряд; – концентрация основных носителей тока;
– подвижность носителей тока.

На дырку, движущуюся в магнитном поле, действует сила Лоренца , где – средняя скорость упорядоченного движения дырок. В установившемся состоянии сила Лоренца равна силе электрического поля: . Тогда

.

Скорость можно найти из выражения для плотности тока

,

где .

.

С учетом этого выражение для электрического поля примет вид

.

Холловская разность потенциалов связана с напряженностью поперечного электрического поля

h.

,

– постоянная Холла.

Таким образом, для определения постоянной Холла следует измерить индукцию магнитного поля (В), ток через образец (I) и толщину образца (b). Зная постоянную Холла, можно определить концентрацию носителей заряда в пластине:

,

постоянная Холла;

Измерения обычно проводят на образце в форме параллелепипеда
(рис. 2), имеющем два торцовых контакта и три боковых. Контакты 1 и 5 служат для создания тока через образец. Постоянное магнитное поле B прикладывается перпендикулярно большой грани образца. В соответствии с эффектом Холла между контактами 2 и 3 образуется холловская разность потенциалов U23. Поскольку с холловскими измерениями часто одновременно проводят измерения удельной электропроводности образца, то на боковой поверхности образца имеется дополнительный контакт 4, который вместе с контактом 3 служит для измерения продольного падения напряжения U23 на расстоянии L между контактами.

Рис.2 Вид образца для Холловских измерений

Для расчета подвижности носителей заряда в исследуемом образце необходимо воспользоваться формулой:

В действительности произведенный элементарный вывод коэффициента Холла неточен: в нем не учтена разница между полной скоростью электронов, входя­щей в выражение магнитной силы, и дрейфовой ско­ростью, которую электрон приобретает под действием электрического поля. Кроме того, не учитывается рас­пределение электронов по скоростям и механизм рас­сеяния носителей. Учет этих явлений может приводить к поправкам, величина которых в предельных случаях не превышает 2 крат.

Для определения индукции магнитного поля можно поступить следующим образом. Катушка медной проволоки, подключенная к веберметру, помещается в зазор сердечника электромагнита. С помощью источника питания при различных напряжениях катушки магнита с веберметра снимается показание магнитного потока.

Магнитная индукция, определяется из формулы:

В – магнитная индукция

Площадь катушки рассчитывается по формуле:

S =р ,

Опытные значения заносятся в таблицу.

Используемое оборудование: источники тока, датчик Холла, электромагнит, измерительные приборы, соединительные провода.

Общая схема установки эффекта Холла приведена на рисунке 3.

Рис.3 Установка для измерения эффекта Холла

Источник тока ИП 1 служит для создания тока через холловский образец. Исследуемый образец помещается в поле электромагнита, питающегося от источника ИП 2. Вольтметр используется для измерения напряжения холла (Uх) или для измерения омического падения напряжения на образце (Uу).

1 Собрать электрическую схему согласно рис.3.

2 Определить, используя веберметр, величину магнитной индукции при различных значениях тока через электромагнит.

3 Вставить образец в магнит, подключить его к 5-ти канальной шине, (перед включением питания убедиться в надежности крепления сердечника);

4 Включить питание магнита и пустить ток через образец, подключить вольтметр для измерения холловской ЭДС к контактам Ux, (переключатель U/Uxпоставить в положение Ux);

5 Комбинацией тумблеров В и I получить 4 значения холловской ЭДС для различных направлений тока и индукции магнитного поля. Для расчета использовать среднее арифметическое полученных значений, взятых по модулю.

6 Для измерения подвижности необходимо использовать 5-ти контактный образец, переключатель U/Ux переключить в положение U, включить питание образца и получить два значения U, изменяя направление тока переключателем I,

7 Рассчитать концентрацию и подвижность носителей заряда

Для выполнения лабораторной работы необходимо выполнить следующие указания:

1. Ток, пропускаемый через образец не должен превышать 100 мА. Для этого датчик Холла необходимо подключить к источнику тока через резистор ограничивающий максимальный ток.

2. Надежно закрепить движущиеся элементы магнитопровода, чтобы исключить возможность механического повреждения датчика Холла.

ВОПРОСЫ И ДЛЯ САМОКОНТРОЛЯ

Источник

Концентрация носителей заряда

Разрешенные зоны содержат большое количество уровней, на каждом из которых могут находиться электроны. Чтобы оценить фактическую концентрацию носителей в полупроводнике, необходимо знать распределение уровней и вероятность их заполнения.

Для невырожденных полупроводников вероятность заполнения уровня W в зоне проводимости дается распределением Максвела–Больцмана:

,

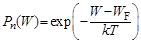
где W_F – энергия, характеризующая уровень Ферми, т.е. уровень, вероятность заполнения которого равна 0,5; k = 1,38 · 10 –23 Дж/ºК – постоянная Больцмана, Т – температура по шкале Кельвина.

Вероятность незаполнения уровня в валентной зоне, т.е. наличия дырки на этом уровне, определяется аналогично:

.

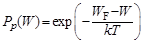
В предположении того, что плотность уровней

,
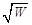
концентрация свободных электронов будет равна:

,

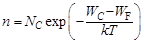
где 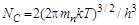, m_n – эффективная масса электрона,
h = 6,63 · 10 –34 Дж · С – постоянная Планка.

Аналогично концентрация дырок

,

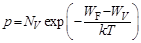
где 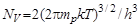, m_p – эффективная масса дырки.

Из произведения концентраций:

видно, что при неизменной температуре произведение концентраций – величина постоянная. Увеличение одной из концентраций сопровождается уменьшением другой.

В собственном полупроводнике концентрации электронов и дырок одинаковы: n_i = p_i (здесь и далее символ i означает собственный полупроводник). Поэтому

.

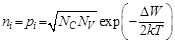
Из этого выражения следует:

1) собственная концентрация носителей заряда очень сильно зависит от ширины запрещенной зоны. Именно поэтому значение n_i для кремния на три порядка меньше, чем для германия;

2) собственная концентрация очень сильно зависит от температуры. При этом влияние температуры тем сильнее, чем больше ширина запрещенной зоны.

Для примесных полупроводников справедливы следующие выражения:

где n_p, p_p – концентрации электронов и дырок в полупроводнике
р-типа; n_n, p_n – концентрация электронов и дырок в полупроводнике
n-типа.

, , , ,

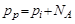
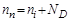
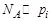
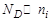
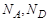
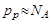
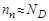
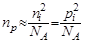
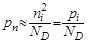
где – концентрации акцепторных и донорных примесей, получим:

, , , .

Отсюда вывод: концентрация неосновных носителей заряда в полупроводнике обратно пропорциональна концентрации примеси.

Важными характеристиками полупроводника являются скорость генерации V_ген и скорость рекомбинации V_рек электронно-дырочных пар:

, ,

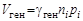
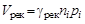
где 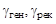– коэффициенты, зависящие от материала полупро-
водника.

Равновесное состояние полупроводника характеризуется тем, что скорость генерации равна скорости рекомбинации: V_ген = V_рек.

Неравновесным состоянием полупроводника называется такое состояние, когда скорость генерации отличается от скорости рекомбинации: V_ген V_рек.

Зная концентрацию электронов и дырок, можно определить значение уровня Ферми:

,

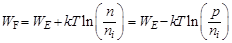
где 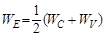– электростатический потенциал полупроводника.

Отсюда можно сделать следующие выводы.

1. В собственных полупроводниках, у которых n = p = n_i, уровень Ферми расположен в середине запрещенной зоны.

2. В электронных полупроводниках (n-типа), у которых 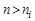, уровень Ферми лежит в верхней половине запрещенной зоны и тем выше, чем больше концентрация электронов.

3. В дырочных полупроводниках (р-типа), у которых 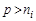, уровень Ферми лежит в нижней половине запрещенной зоны и тем ниже, чем больше концентрация дырок.

4. С ростом температуры, когда примесный полупроводник постепенно превращается в собственный, уровень Ферми смещается к середине запрещенной зоны.

Одно из фундаментальных положений в физике полупроводников формулируется следующим образом: уровень Ферми одинаков во всех частях равновесной системы, какой бы она ни была.

Источник

Концентрации носителей заряда в полупроводниках

КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ И ОСНОВНЫЕ

РАСЧЕТНЫЕ ФОРМУЛЫ

Проводниковые материалы

Плотность тока в проводнике с одним типом носителей заряда

Удельная электрическая проводимость металла

В соответствии с классической электронной теорией металлов выра­жение для удельного электрического сопротивления имеет вид

Если атомы в металле ионизированы однократно, то концентрация свободных электронов n будет равна концентрации атомов N и может быть рассчитана по формуле

В соответствии с квантовой теорией удельное электрическое сопро­тивление металлов

Средняя скорость дрейфа за время свободного пробега

где τ₀ – время свободного пробега.

Среднюю скорость можно также найти по формулам

В промежутках между столкновениями с узлами кристаллической решетки электрон при воздействии электрического поля движется с ускорением

Удельная проводимость проводника может быть определена как

g = (e 2 * n * l)/(m₀ * u),

где u – средняя скорость теплового движения (температуре 300 К соответствует средняя скорость порядка 10 5 м/с).

Время дрейфа электрона по проводнику t = l/v.

Время пролета при движении электрона без соударений t_пр = .

Влияние примесей и структурных дефектов на удельное сопро­тивление. Примеси и структурные дефекты увеличивают удельное сопро­тивление металлов. В соответствии с правилом Маттиссена

Удельное сопротивление металлических сплавов, имеющих струк­туру неупорядоченного твердого раствора, ρ_ост может существенно пре­вышать ρ_т. Для многих двухкомпонентных сплавов металлов, не принад­лежащих к числу переходных или редкоземельных элементов, зависимость ρ_ост от состава описывается законом Нордгейма

Влияние температуры на сопротивление и длину проводника. В диапа­зоне температур, где зависимость ρ от Т близка к линейной, справедливо выражение

Температурные коэффициенты удельного сопротивления a_r, сопротивления a_R и удлинения a_l связаны соотношением

Температурный коэффициент сопротивления

Зависимость длины проводника от температуры

где l₀ – начальная длина проводника при температуре Т₀;

l – длина при температуре Т;

α_l – температурный коэффициент линейного удлинения.

Количество теплоты Q, выделяющееся в единицу времени в единице объема проводника, по которому протекает ток плотностью J, при напряженности электрического поля E, выражается формулой

Внутренняя контактная разность потенциалов при соприкосновении металлов А и В

причем уровни Ферми отсчитываются от дна зоны проводимости.

Связь между концентрацией электронов и энергией Ферми

n = (8p/3) * (2m₀/h 2 ) 3/2 * (W_F) 3/2

Разность потенциалов на концах последовательной разнородной цепи

где А_н, А_к – работа выхода электронов из начального и конечного проводников; l – расстояние между ними.

Примечание: если работа выхода выражена в эВ, величина е в знаменателе отсутствует.

Термоэлектродвижущая сила (термоЭДС). В однородном провод­нике при наличии градиента температуры на его концах возникает раз­ность потенциалов. Ее значение, отнесенное к единичной разности темпе­ратур на концах проводника, называют абсолютной удельной термоЭДС. В термоэлектрической цепи, составленной из разнородных проводников (термопаре), относительная удельная термоЭДС представляет собой разность абсолютных удельных термоЭДС составляющих провод­ников

Сопротивление проводников на высоких частотах. На высоких частотах наблюдается неравномерное распределение электрического тока по сечению проводника: плотность тока максимальна на поверхности и убывает по мере проникновения вглубь проводника. Распределение тока по сечению проводника описывается уравнением

Плотность тока изменяется по тому же закону, что и напряженность электрического поля E, так как J = γE. Связь глубины проникновения поля с физическими характеристиками вещества определяется выражением

Так как центральная часть сечения проводника почти не использует­ся, активное сопротивление провода R

при прохождении по нему пере­менного тока больше, чем его активное сопротивление R₀ при постоянном токе. Коэффициент увеличения сопротивления k_R рассчитывается по фор­муле

,

Полупроводники

Удельная электрическая проводимость полупроводника

где n, p – концентрация электронов и дырок соответственно;

μ_n, μ_p – подвижности электронов и дырок.

В примесных полупроводниках одним из слагаемых, в зависимости от типа проводимости, можно пренебречь.

Концентрации носителей заряда в полупроводниках

Собственная концентрация носителей заряда (электронов и дырок)

Концентрации электронов и дырок в примесных полупроводниках

Концентрации носителей заряда связаны с собственной концентра­цией носителей соотношением «действующих масс»

Уровень Ферми в собственном полупроводнике

,

где W_i – уровень, соответствующий середине запрещенной зоны.

Вероятность заполнения энергетического уровня W электроном и дыркой при температуре T:

— для собственного полупроводника (статистика Максвелла-Больцмана)

— для примесного полупроводника (статистика Ферми-Дирака)

Уровень Ферми в примесных полупроводниках:

; .

Концентрации основных носителей n и p в электронном и дырочном полупроводниках соответственно при температурах частичной иониза­ции примесных атомов

Концентрации основных носителей в примесных полупроводниках при температурах полной ионизации атомов примеси и пренебрежимо низ­кой концентрации собственных носителей

Источник