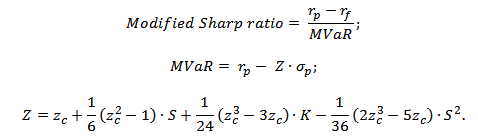коэффициент шарпа что это формула расчета
Коэффициент Шарпа — что он показывает, формула и расчет
Доброго времени суток уважаемые читатели проекта Тюлягин! В сегодняшней статье мы поговорим о финансовых показателях и рассмотрим коэффициент Шарпа. В данной статье вы узнаете что такое коэффициент Шарпа, о чем говорит и что он показывает инвестору и аналитику. Также приведена формула для расчета коэффициента Шарпа с примерами. Кроме этого даны другие особенности и ответы на наиболее популярные вопросы о коэффициента Шарпа. Об этом и не только далее в статье.
Содержание статьи:
Что такое коэффициент Шарпа?
Коэффициент Шарпа был разработан лауреатом Нобелевской премии Уильямом Ф. Шарпом и используется, чтобы помочь инвесторам понять доходность инвестиций по сравнению с их риском. Коэффициент Шарпа — это средний доход, полученный сверх безрисковой ставки на единицу волатильности или общего риска. Волатильность — это мера колебаний цены актива или портфеля.
Формула и расчет коэффициента Шарпа
Коэффициент Шарпа = (Rp — Rf) \ σ p
Rp — возврат портфеля
Rf — risk-free rate
σ p — стандартное отклонение сверхдоходности портфеля
Коэффициент Шарпа рассчитывается следующим образом:
О чем может рассказать коэффициент Шарпа
Вычитание безрисковой ставки из средней доходности позволяет инвестору лучше изолировать прибыль, связанную с рискованной деятельностью. Безрисковая процентная ставка (безрисковая норма доходности) — это возврат инвестиций с нулевым риском, то есть доход, на который инвесторы могут рассчитывать, не принимая на себя риска. Например, доходность казначейских облигаций США может использоваться как безрисковая ставка.
Как правило, чем больше значение коэффициента Шарпа, тем привлекательнее доход с поправкой на риск.
Коэффициент Шарпа — один из наиболее широко используемых методов расчета доходности с поправкой на риск. Современная теория портфеля утверждает, что добавление активов в диверсифицированный портфель с низкой корреляцией может снизить риск портфеля без ущерба для доходности.
Добавление диверсификации должно увеличить коэффициент Шарпа по сравнению с аналогичными портфелями с более низким уровнем диверсификации. Чтобы это было правдой, инвесторы также должны принять допущение о том, что риск равен волатильности, что не является необоснованным, но может быть слишком узким, чтобы применяться ко всем инвестициям.
Коэффициент Шарпа можно использовать для оценки прошлой доходности портфеля (постфактум), где в формуле используется фактическая доходность. В качестве альтернативы инвестор может использовать ожидаемую доходность портфеля и ожидаемую безрисковую ставку для расчета предполагаемого коэффициента Шарпа (прогнозируемого).
Коэффициент Шарпа также может помочь объяснить, является ли избыточная доходность портфеля результатом разумных инвестиционных решений или результатом слишком большого риска. Хотя один портфель или фонд может иметь более высокую доходность, чем его аналоги, это хорошее вложение только в том случае, если эта более высокая доходность не сопряжена с превышением дополнительного риска.
Чем выше коэффициент Шарпа портфеля, тем лучше его показатели с поправкой на риск. Если анализ приводит к отрицательному коэффициенту Шарпа, это означает, что либо безрисковая ставка больше, чем доходность портфеля, либо ожидается, что доходность портфеля будет отрицательной. В любом случае отрицательный коэффициент Шарпа не несет никакого полезного значения.
Пример использования коэффициента Шарпа
Коэффициент Шарпа часто используется для сравнения изменения общих характеристик риска и доходности при добавлении нового актива или класса активов в портфель.
Например, инвестор рассматривает возможность добавления хедж-фонда в свой существующий портфель, который в настоящее время разделен между акциями и облигациями и принес 15% прибыли за последний год. Текущая безрисковая ставка составляет 3,5%, а волатильность доходности портфеля составляет 12%, что дает коэффициент Шарпа 95,8% или (15% — 3,5%), деленный на 12%.
Инвестор считает, что добавление хедж-фонда в портфель снизит ожидаемую доходность до 11% в следующем году, но также ожидает, что волатильность портфеля снизится до 7%. Он предполагает, что безрисковая ставка в ближайший год останется прежней.
Используя ту же формулу с расчетными будущими цифрами, инвестор находит, что портфель имеет ожидаемый коэффициент Шарпа 107%, или (11% — 3,5%), деленный на 7%.
Здесь инвестор показал, что, хотя вложение в хедж-фонд снижает абсолютную доходность портфеля, оно улучшило его эффективность с поправкой на риск. Если добавление новой инвестиции снизило коэффициент Шарпа, ее не следует добавлять в портфель. В этом примере предполагается, что коэффициент Шарпа, основанный на прошлой производительности, можно справедливо сравнить с ожидаемой будущей производительностью.
Разница между коэффициентом Шарпа и коэффициентом Сортино
Разновидностью коэффициента Шарпа является коэффициент Сортино, который устраняет влияние восходящих движений цены на стандартное отклонение, чтобы сосредоточиться на распределении доходов, которые ниже целевого или требуемого дохода.
Коэффициент Сортино также заменяет безрисковую ставку требуемой доходностью в числителе формулы, делая формулу доходности портфеля за вычетом требуемой доходности, деленной на распределение доходностей ниже целевого или требуемого дохода.
Другой вариант коэффициента Шарпа — коэффициент Трейнора, который использует бета-коэффициент портфеля или корреляцию, которую портфель имеет с остальным рынком. Бета — это показатель волатильности и риска инвестиций по сравнению с рынком в целом.
Цель коэффициента Трейнора — определить, получает ли инвестор компенсацию за принятие дополнительного риска, превышающего неотъемлемый риск рынка. Формула коэффициента Трейнора — это доходность портфеля за вычетом безрисковой ставки, деленная на бета-коэффициент портфеля.
Ограничения использования коэффициента Шарпа
Коэффициент Шарпа использует стандартное отклонение доходности в знаменателе как показатель общего риска портфеля, который предполагает, что доходность распределяется нормально. Нормальное распределение данных похоже на бросание пары игральных костей. Мы знаем, что при большом количестве бросков наиболее частым результатом игры в кости будет семь, а наименее частыми — двумя и двенадцатью.
Однако доходность на финансовых рынках отклоняется от среднего из-за большого количества неожиданных падений или скачков цен. Кроме того, стандартное отклонение предполагает, что движение цены в любом направлении одинаково рискованно.
Управляющие портфелями могут манипулировать коэффициентом Шарпа, стремясь повысить свою очевидную историю доходности с поправкой на риск. Это можно сделать, увеличив интервал измерения. Это приведет к заниженной оценке волатильности. Например, среднегодовое стандартное отклонение дневной доходности обычно выше, чем у еженедельной доходности, которое, в свою очередь, выше, чем у ежемесячной доходности.
Выбор периода для анализа с наилучшим потенциальным коэффициентом Шарпа, а не нейтрального периода ретроспективного анализа, — это еще один способ тщательно отобрать данные, которые будут искажать доходность с поправкой на риск.
Популярные вопросы о коэффициенте Шарпа
Что такое коэффициент Шарпа?
Коэффициент Шарпа — это финансовый показатель, который часто используется инвесторами при оценке эффективности активов и управления инвестиционными продуктами и портфелями. Он состоит из взятия избыточной доходности портфеля относительно безрисковой ставки и деления ее на стандартное отклонение избыточной доходности портфеля. По идее, это дает измерение превосходства портфеля на единицу волатильности портфеля. При прочих равных, портфели с более высокой избыточной доходностью или более низкой волатильностью будут иметь более высокий коэффициент Шарпа, и наоборот.
Какой коэффициент Шарпа «хороший»?
Коэффициенты Шарпа выше 1,00 обычно считаются «хорошими», поскольку это предполагает, что портфель предлагает избыточную доходность по сравнению с его волатильностью. При этом инвесторы часто сравнивают коэффициент Шарпа портфеля с аналогичными портфелями. Следовательно, портфель с коэффициентом Шарпа 1,00 может считаться неадекватным, если у конкурентов в аналогичной группе портфелей средний коэффициент Шарпа выше 1,00.
Как рассчитывается коэффициент Шарпа?
Для расчета коэффициента Шарпа инвесторы сначала вычитают безрисковую ставку из нормы доходности портфеля, часто используя доходность государственных облигаций (казначейских облигаций) в качестве прокси для безрисковой нормы доходности. Затем они делят результат на стандартное отклонение избыточной доходности портфеля. Обратите внимание, что при использовании стандартного отклонения эта формула неявно предполагает, что доходность портфеля нормально распределяется, что на самом деле может быть не так.
Резюме
А на этом сегодня все про Коэффициент Шарпа. Надеюсь статья оказалась для вас полезной. Делитесь статьей в социальных сетях и мессенджерах и добавляйте сайт в закладки. Успехов и до новых встреч на страницах проекта Тюлягин!
Коэффициент Шарпа. Что это. Формула расчета. Пример в Excel
Рассмотрим один из классических коэффициентов оценки паевых инвестиционных фондов (ПИФов) и инвестиционных портфелей – коэффициент Шарпа.
Коэффициент Шарпа (англ. Sharp ratio) – это показатель оценивающий эффективность и результативность управления инвестиционным портфелем (паевым инвестиционным фондом). Данный коэффициент был разработан У. Шарпом в 1966 году и применяется для оценки, как уже действующих стратегии управления, так и для сравнительного анализа различных альтернативных стратегий инвестирования.
Коэффициент Шарпа используется в оценке: качества управления паевых инвестиционных фондов (ПИФов), результативности активных торговых стратегий на фондовом рынке, эффективности формирования инвестиционных портфелей инвесторов.
Коэффициент Шарпа представляет собой относительный показатель доходность-риска инвестиционного фонда (ПИФа) и отражает во сколько раз уровень избыточной доходности выше уровня риска инвестиции (инвестиционного портфеля, ПИФа, акции и т.д.).
Инфографика. Коэффициент Шарпа (основные моменты)
Оценка стоимости бизнеса | Финансовый анализ по МСФО | Финансовый анализ по РСБУ |
Расчет NPV, IRR в Excel | Оценка акций и облигаций |
Формула расчета коэффициента Шарпа
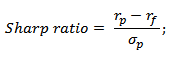
rp – средняя доходность паевого инвестиционного фонда (инвестиционного портфеля);
rf – средняя доходность безрискового актива;
σp – стандартное отклонение доходностей активов паевого инвестиционного фонда (риск инвестиционного портфеля).
Рассмотрим более подробно, как рассчитать каждый из показателей формулы.
 | ★ Excel таблица для формирования инвестиционного портфеля ценных бумаг (рассчитай портфель за 1 минуту) + оценка риска и доходности |
 | ★ Программа InvestRatio — расчет всех инвестиционных коэффициентов в Excel за 5 минут (расчет коэффициентов Шарпа, Сортино, Трейнора, Калмара, Модильянки бета, VaR) + прогнозирование движения курса |
Расчет доходности безрискового актива
Для оценки избыточной доходности, которую получил инвестор необходимо рассчитать минимальную возможную доходность, которую он мог бы получить при вложении в абсолютно надежные активы. Именно избыточная доходность отражает качество управления и эффективность принимаемых решений менеджером паевого инвестиционного фонда.
Существуют несколько способов оценки доходности безрискового актива:
В результате необходимо сопоставить доходность полученную за счет управления рискованными ценными бумагами и минимальный уровень доходность абсолютно надежного актива.
Оценка паевого инвестиционного фонда по коэффициенту Шарпа
Оценка показателя Шарпа представлена в таблице ниже. К примеру, если показатель больше единицы, значит уровень избыточной доходности выше нежели существующий риск фонда или инвестиционного портфеля. Оценка показателя позволяет выбрать наиболее инвестиционно привлекательные фонды, портфели или стратегии для вложения.
| Значение показателя | Оценка эффективности управления |
| Sharp ratio >1 | Высокая результативность управления паевым инвестиционным фондом или портфелем. Данный фонд привлекателен для вложения |
| 1>Sharp ratio >0 | Уровень риска выше, нежели значение избыточной доходности паевого инвестиционного фонда. Необходимо рассмотреть другие показатели инвестиционной привлекательности фонда |
| Sharp ratio Sharp ratio2 | Первый паевой инвестиционный фонд более привлекателен для вложения, чем второй |
Пример выбра паевого инвестиционного фонда по коэффициенту Шарпа
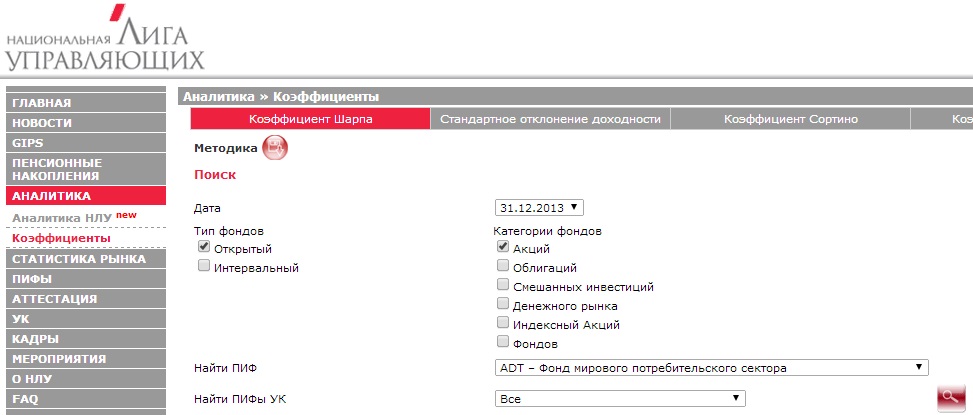
Информацию о существующих фондах можно получить на сайте nlu.ru (национальная лига управляющих). Заходим на сайт и выбираем раздел «АНАЛИТИКА».→ «Коэффициент» → «Коэффициент Шарпа». В системе есть возможности отфильтровать по различным параметрам фонды: по типу, по управляющей компании, по категории и дате.
Оценка паевых инвестиционных фондов на основе коэффициента Шарпа
На рисунке ниже будет отражаться ранжирование всех паевых инвестиционных фондов по коэффициенту Шарпа. Так фонд «РЕГИОН Фонд акций» имеет максимальное значение коэффициента Шарпа, что свидетельствует о высоком качестве управления.
Оценка ПИФов на основе их эффективности управления
Пример оценки коэффициента Шарпа для инвестиционного портфеля
Если вы формируете сами инвестиционный портфель и вам необходимо сравнить различные портфели ценных бумаг, то для этого необходимо получить котировки изменения всех акций входящий в портфель, рассчитать их доходность и общий риск портфеля. Рассмотрим более подробно пример расчета коэффициента Шарпа в программе Excel.
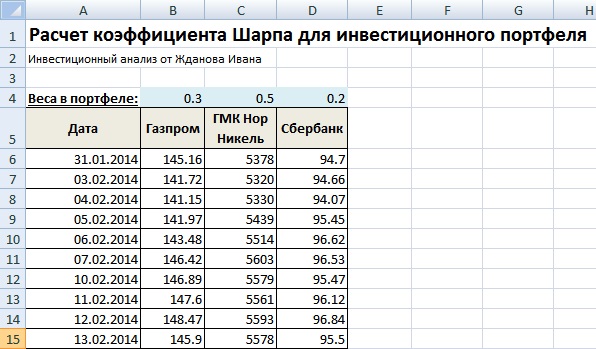
Получить котировки можно с сайта finam.ru в разделе «Про рынок» → «Экспорт данных». Возьмем портфель из трех акций: ОАО «Газпром», ОАО «ГМК Норильский Никель» и ОАО «Сбербанк». Для каждой акции оценим долю в общем портфеле, так у Газпрома – 0,3, ГМК Нор. Никель – 0,5 и Сбербанк – 02. Для анализа брались котировки в течение года с 31.01.2014 – 31.01.2015.
Расчет коэффициента Шарпа для инвестиционного портфеля в Excel
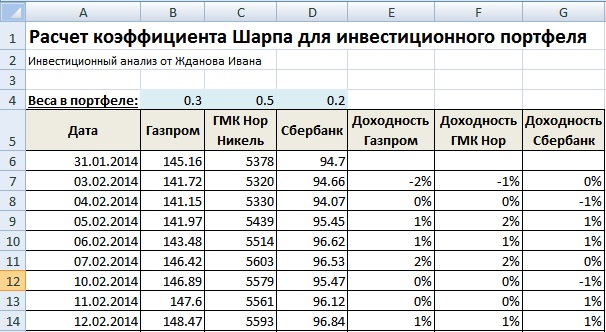
На следующем этапе необходимо рассчитать доходность по каждой ценной бумаге портфеля. Для этого воспользуемся формулой в Excel:
Доходность акции Газпром =LN(B7/B6)
Доходность акции ГМК Нор. Никель =LN(C7/C6)
Доходность акции Сбербанк =LN(D7/D6)
Оценка доходности акций инвестиционного портфеля
Далее необходимо рассчитать параметры коэффициента: доходность и риск портфеля в целом, а также оценить безрисковую доходность. Доходность портфеля представляет собой взвешенную сумму среднеарифметических дневных доходностей, риск портфеля равен взвешенной сумме стандартных отклонений доходностей акций.
Безрисковая доходность была взята как годовая процентная ставка по депозиту в банке и составляет 12%. Воспользуемся следующими формулами оценки:
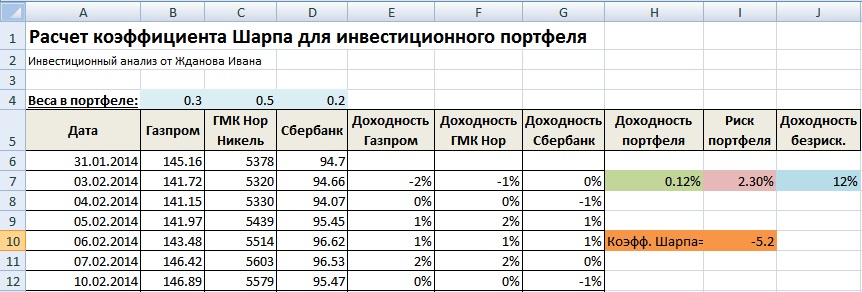
Доходность портфеля =СРЗНАЧ(E7:E256)*B4+СРЗНАЧ(F7:F256)*C4+СРЗНАЧ(G7:G256)*D4
Риск портфеля =СТАНДОТКЛОН(E7:E256)*B4+СТАНДОТКЛОН(F7:F256)*C4+СТАНДОТКЛОН(G7:G256)*D4
Коэффициент Шарпа =(H7-J7)/I7
Оценка эффективности инвестиционного портфеля по коэффициенту Шарпа
Как мы видим значения показателя Шарпа отрицательное, это говорит о том, что данный инвестиционный портфель сформирован неправильно и его следует пересмотреть. Доходность по безрисковому активу оказалась выше, чем сама доходность по акциям. Инвестору целесообразнее было вложиться в безрисковый актив нежели активно управлять и нести дополнительные риски. Более подробно узнать про коэффициенты оценки эффективности инвестиций вы можете в статье: «Оценка эффективности инвестиций, инвестиционного портфеля, акций на примере в Excel«.
Модифицированный коэффициент Шарпа
Классический коэффициент Шарпа имеет ряд недостатков, которые решены в его модификации. Модификация показателя главным образом затрагивает изменение оценки риска инвестиционного портфеля. Для оценки риска используется не только стандартное отклонение как мера изменчивости доходности портфеля, а модифицированная мера риска VaR (Value at Risk). Данная мера позволяет оценить более реалистично будущие убытки за счет оценки характера распределения исторической доходности акций. Формула расчета его следующая:
где: rp – средняя доходность инвестиционного портфеля; rf – средняя доходность безрискового актива; σp – стандартное отклонение доходностей инвестиционного портфеля; S –эксцесс распределения доходностей; zc – куртозис распределения доходностей портфеля; K – квантиль распределения доходностей.
Оценка риска в данной модели основывается исключительно на статистическом расчете, что позволяет более адекватно оценить риски инвестиционного портфеля или паевого инвестиционного фонда.
 | ★ Программа InvestRatio — расчет всех инвестиционных коэффициентов в Excel за 5 минут (расчет коэффициентов Шарпа, Сортино, Трейнора, Калмара, Модильянки бета, VaR) + прогнозирование движения курса |
Где применяется коэффициент Шарпа
Одним из направлений применения коэффициента Шарпа является сравнение и оценка эффективности инвестиционных портфелей, Фондов (ETF, REIT и др.), торговых стратегий. Сравнить инвестиционные портфели только по полученной доходности или только по риску (убыткам) не грамотно. Поэтому для определения результативности используется интегральный показатель, включающий доходность и риск. Чем выше значение коэффициента Шарпа, тем эффективнее инвестиционный портфель.
Смоделировать портфель можно в сервисе portfoliovisualizer.com. Для этого возьмем акции «большой четверки»: Apple (APPL), Google (GOOG), Amazon (AMZN), Facebook (FB). Первый портфель создадим без оптимизации весов акций. У каждой акции будет равный вес по 25%. Второй портфель оптимизируем по максимизации коэффициента Шарпа.
Максимизация коэффициента Шарпа позволяет найти оптимальные доли акций в портфеле
В оптимизированном портфеле изменятся веса акций ↓
| Тикер | Название | Вес нового портфеля |
| AMZN | Amazon. | 44.29% |
| GOOG | Alphabet | 5.43% |
| FB | 27.11% | |
| AAPL | Apple | 23.18% |
В таблице ниже представлены доходности и риски за 10-й период. Как видим, несмотря на небольшое увеличение волатильности портфеля, прибыльность выше.
| Портфель | Доходность за 10 лет | Риск (средняя волатильность) | Коэффициент Шарпа |
| Портфель с равными весами | 840% | 20,8% | 3,06 |
| Оптимизированный портфель | 1030% | 22,6% | 3,20 |
Наши портфели имеют коэффициент Шарпа больше 3, это говорит о том, что подобранные акции позволяют создавать доходность в 3 раза превышающую риски (выраженные в волатильности).
На рисунке ниже отражена динамика доходности первого и второго портфеля.
Оптимизация портфеля по коэффициенту Шарпа позволяет ребалансировать портфель, увеличит прибыль при незначительном увеличении риска
Проблема коэффициента Шарпа
Один из недостатков коэффициента Шарпа является использование за меру риска — стандартное отклонение (σ). Эта статистический критерий показыает измнчивость доходностей и отражает отклонение от среднеарифметического доходностей как в положительную, так и отрицательную сторону. Но ведь отклонение в положительную сторону выгодно инвестору и его можно считать как прибыль. Решение данного противоречия измерения риска предложил Сортино, который заменил стандарное отклонение — «стандартным отклонением вниз». Более подробно про коэффициент Сортино читайте в статье: → Коэффициент Сортино. Интерпретация. Пример расчета.
Резюме
Коэффициент Шарпа является классическим показателем оценки результативности управления инвестиционным портфелем, паевым инвестиционным фондов или даже вложения в отдельную акцию. Чем выше значения показателя, тем большая сверхдоходность была получена управляющим. Для быстрой оценки коэффициента Шарпа можно воспользоваться сервисом «НЛУ», а для оценки стратегии собственного инвестиционного портфеля необходимо провести расчет в Excel. Модификация показателя позволяет решить вопрос более реалистичной оценки риска за счет использования статистических показателей распределения исторической доходности. С вами был Иван Жданов.
Автор: к.э.н. Жданов Иван Юрьевич