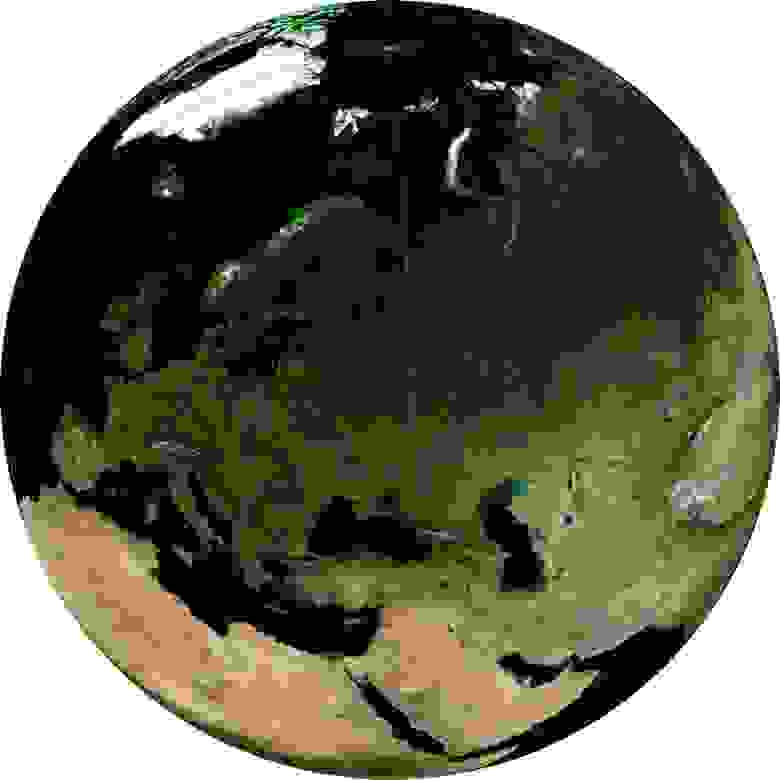
что такое зона картографической проекции
aistikb
Особенности формирования технических планов по 6-й версии схемы
Общая информация
Системы координат и зоны картографической проекции
Вот такое описание данных сведений содержится в описании новой схемы:
Мы добавили в справочник систем координат возможность добавлять сведения о зонах картографической проекции (КП) для каждой СК. Для дальнейшей работы существующий список систем координат следует сохранить и ввести новые уже с заполнением реквизитов кода субъекта РФ и сведений о зонах КП.
Подробное описание о работе с данным справочником приведено здесь.
При вводе технического плана в Системе сведения о СК приводятся в разделе «Исходные данные» вкладка «Геодезическая основа».
Номер зоны картографической проекции задается для каждого контура в разделе «Местоположение и сведения о частях» на вкладке «Пространственные координаты». При формировании технического плана для одновременного образования нескольких объектов недвижимости сведения приводятся в отношении каждого образуемого объекта.
Сведения о состоянии пункта геодезической сети
При оформлении технического плана в xml версии 3 сведения о состоянии пункта приводили в заключении кадастрового инженера.
В новой схеме данные сведения в xml документе технического плана приводятся в структурированном виде. Теперь нет необходимости приводить их в заключении кадастрового инженера.
В Системе данные сведения заполняются в разделе «Исходные данные» на вкладке «Геодезическая основа».
Планы этажей (план объекта недвижимости)
В соответствии с п. 11 и п. 21 Требований планы этажей или план объекта недвижимости (при отсутствии этажности) обязательно включается в состав технического плана в формате JPEG.
Привести данные сведения в xml технического плана сформированного по схеме версии 3 не было возможности. В связи с эти планы этажей (план объекта недвижимости) прикрепляли в виде многостраничного PDF в виде документа приложения к техническому плану.
В Системе для формирования технического плана по новой схеме данные сведения необходимо заполнять в разделе «Планы этажей». При наличии этажности для каждого плана необходимо указать тип и номер этажа в соответствующем поле. При отсутствии этажности поле «тип и номер этажа» следует оставить пустыми. При формировании технического плана для одновременного образования нескольких объектов недвижимости сведения приводятся в отношении каждого образуемого объекта.
Схема, Чертеж и Схема геодезических построений
В xml технического плана сформированного по 3-й версии схемы можно было включить только один файл Схемы, один файл Чертежа и один файл Схемы геодезических построений.
Новая схема позволяет приводить один и более файл для каждого типа графического приложения. Все они должны быть в формате PDF.
В Системе данные сведения заполняются в разделе «Графическая часть». Если необходимо более одного графического вложения, то сведения о втором и последующих приводятся в разделе «Все приложения» на вкладке «Графика». Для приложения необходимо выставить соответствующий атрибут «Чертеж контура объекта», «Схема расположения объекта на ЗУ» или «Схема геодезических построений».
Сведения о графических приложениях приводятся в отношении документа (технического плана).
Описание части здания
При описании образуемой или изменяемой части здания для выгрузке по xml схеме версии 3 обязательно необходимо приводить описание ее расположения в виде контура. Дополнительно можно было приводить описание расположения в виде плана в формате JPG, с его привязкой к этажу и номерам помещения на плане.
Новая схема определяет описание расположение части одним из видов: либо в виде контура, либо в виде описание расположения в здании.
В Системе описание расположения части следует приводить или контуром или в виде расположения в здании (номера помещений, этаж, план). Если для части приведено описание и виде контура и в виде расположения части в здании, то в xml по 6-й версии будет выгружено только описание в виде контура.
Приложения
Согласно п. 11 Требований раздел Приложения является обязательным для включения в состав любого технического плана. Xml схема технического плана версии 6 требует наличия в составе приложения минимум одного файла.
При формировании xml Системой в состав приложения включаются все документы с атрибутом «Приложение к техническому плану».
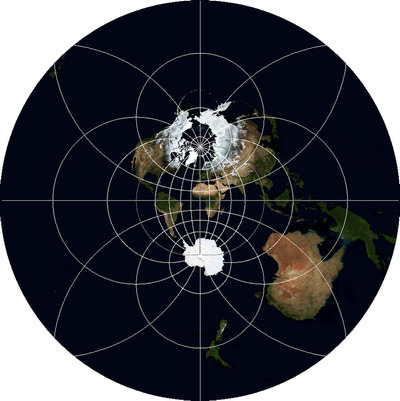
Ликбез по картографическим проекциям с картинками
Визуализация данных самого разного рода, имеющих некое географическое распределение, в последнее время получает все большее и большее распространение. Тут, на Хабре, статьи с картами встречаются чуть ли не каждую неделю. Карты в статьях очень разные, но роднит их одно: как правило, в них используются всего две картографические проекции, при том — не самые удачные из существующих. Мне бы хотелось дать несколько наглядных примеров проекций, которые выглядят более эстетично и лучше приспособлены для разных видов визуализации. В этой статье будут рассмотрены общемировые проекции и проекции большей части Земли, так как визуализация чего-либо на карте мира, пожалуй, является наиболее распространенной из подобных задач.
Легкое введение
Поскольку статья ориентирована на вопросы визуализации данных, я не буду касаться глубоко теории проекций (датумов, конформности, равноугольности и тому подобного), кроме общих принципов их построения. Также, я буду говорить тут о «проекциях», формально подразумевая «систему координат», coordinate reference system, потому что для карт таких масштабов не имеет смысла отдельно рассматривать проекцию и датум. Математики здесь тоже практически не будет, кроме простой геометрии. Желающие ознакомиться с математическими принципами, могут это сделать по статьям на Wolfram MathWorld. Так что изучающим программирование в области геоинформационных систем или их опытным пользователям, эта статья, возможно, будет не очень полезна.
Перед началом, объясню пару вещей. Все примеры будут даваться с использованием набора данных государственных границ с вот этого сайта и набора данных Blue Marble Next Generation с сайта NASA. Последний включает в себя синтезированные безоблачные снимки земной поверхности за каждый из двенадцати месяцев 2004-го года, что позволит внести некоторое разнообразие в иллюстрации.
Я очень люблю открытый софт, но использовать GDAL в данном случае мне показалось неэффективно — некоторых не очень ходовых, но полезных проекций в его реализации на данный момент либо нет, либо я плохо смотрел исходники, а потому иллюстрации я готовил в коммерческой программе GlobalMapper, которой пользуюсь уже много лет, и которая славится поддержкой внушительного списка систем координат.
Названия проекций и некоторые термины я буду давать и англоязычные, потому что если кому-то захочется поискать материалы по этой теме, русскоязычных источников в сети найдется несколько меньше (объем статей в Википедии на русском меньше в несколько раз). Для большинства проекций я постараюсь дать не только названия, но и коды EPSG и/или WKID, а также название проекции в библиотеке PROJ.4, широко используемой в открытом софте (например, в пакете R) для поддержки систем координат.
Некоторые проекции, возможно, окажутся кому-то знакомыми по картинке с xkcd, но все из них тут рассмотрены не будут.
Проблема
Начнем с того, что же это за самые распространенные проекции, и что с ними не так.
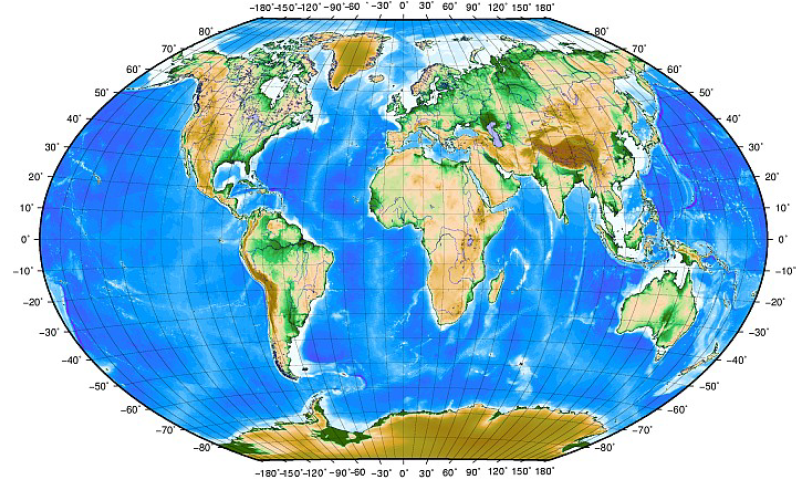
Первая проекция — так называемая «Географическая», она же – Geographic projection, Latitude/Longitude, Plate carrée EPSG:4326 WKID:54001 PROJ.4:longlat. Строго говоря, она даже не совсем является проекцией, потому что получается путем интерпретации полярных угловых координат, как линейных прямоугольных, без всяких вычислений. Эту проекцию используют, потому что она способна отобразить всю поверхность Земли целиком и потому, что она самая простая математически, а данные очень часто распространяются не спроецированными, то есть именно в географических координатах (градусах широты и долготы).
Другая весьма популярная проекция — «проекция Меркатора», Mercator projection PROJ.4:merc. Она также используется для визуализации данных, покрывающих весь мир, но ее популярность продиктована не только простотой — ее варианты являются стандартом де-факто для глобальных картографических сервисов, таких как Google Maps, Bing Maps, Here. С ней глубоко связаны картографические библиотеки OpenLayers, Leaflet, API упомянутых выше сервисов. В варианте Google и OpenStreetMap она носит название Web Mercator и имеет код EPSG/WKID:3857, иногда на нее также ссылаются, как на EPSG:900913. Принцип ее построения не сильно сложнее Географической – это проекция на цилиндр, чья ось совпадает с географической осью Земли, проецирование происходит линиями, выходящими из центра планеты, от чего ошибка растяжения приполярных областей по горизонтали оказывается скомпенсирована пропорциональным растяжением по вертикали. Проблема с этим только в том, что карта получится слишком большой по вертикали, если попытаться отобразить и север Гренландии. Потому обычно отбрасывают 16° полярных областей (в равной пропорции или больше — с юга).
На чей-то взгляд выглядит чуть лучше, чем Географическая, но одну проблему мы уже упомянули, а вторая — чем ближе объект к полюсам, тем он кажется больше, хотя его форма уже не так искажена. Потому, если предмет визуализации — плотность маркеров на единицу территории или расстояния, такой способ отображения будет вводить в заблуждение. При грамотном выборе способа визуализации, конечно, это можно скомпенсировать, а для каких-то случаев это вообще не проблема: например, если величина какого-то показателя в целой стране соотнесена с цветом этой страны на карте, эффект растяжения площадей не сказывается. Эта проекция сохраняет только форму объектов, потому очертания континентов и стран выглядят довольно узнаваемо. И, как я уже сказал, она — ваш первый и самый простой вариант при создании интерактивных веб-карт.
Варианты решения
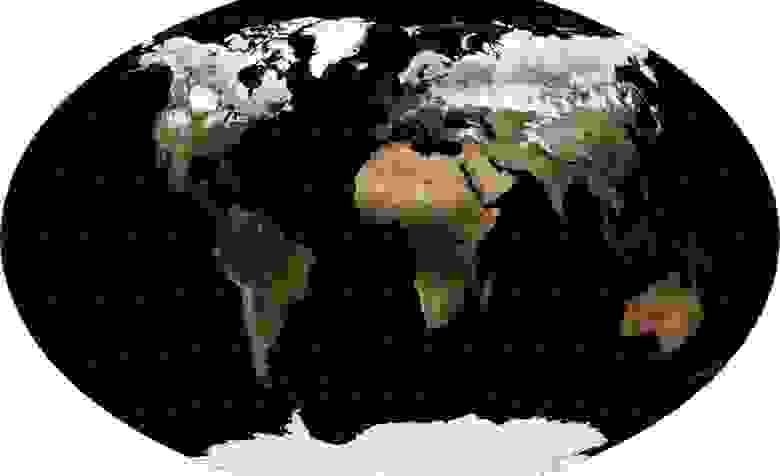
Что же делать с глобальными данными, если нам по какой-то причине понадобилась проекция, лучше сохраняющая такие свойства объектов, как форма, площадь, расстояния и углы? Законы геометрии не дают нам сохранить все эти свойства сразу, развернув круглую поверхность Земли на плоскость. Однако, для визуализации данных более всего важна эстетика и восприятие, а не сохранение свойств, как для навигационных или измерительных задач. Потому становится возможным подобрать такую проекцию, искажения в которой были бы равномерно распределены по свойствам. И таких проекций существует довольно много. Существуют три самых известных, обладающих сходными свойствами: «Тройная проекция Винкеля» Winkel Tripel WKID:54042 PROJ.4:wintri, «проекция Робинсона» Robinson projection WKID:54030 PROJ.4:robin, «проекция Каврайского» (Kavrayskiy projection). Первая и последняя имеют визуально минимальные искажения, а неспециалисту, не видя градусной сетки, вообще весьма сложно различить их, потому я приведу иллюстрацию для Winkel Tripel, как той, которая лично мне нравится больше всего.
Вот так описание этой проекции выглядит в формате ESRI WKT:
PROJCS[«Robinson»,
GEOGCS[«GCS_WGS_1984»,
DATUM[«D_WGS84»,
SPHEROID[«WGS84»,6378137,298.257223563]
],
PRIMEM[«Greenwich»,0],
UNIT[«Degree»,0.017453292519943295]
],
PROJECTION[«Robinson»],
PARAMETER[«central_meridian»,0],
PARAMETER[«false_easting»,0],
PARAMETER[«false_northing»,0],
UNIT[«Meter»,1]
]
Как легко видеть, хотя искажение контуров и некоторое увеличение площади стран к полюсам здесь также наблюдаются, но это нельзя даже сравнивать с растяжением Географической проекции и пропорциональным увеличением проекции Меркатора.
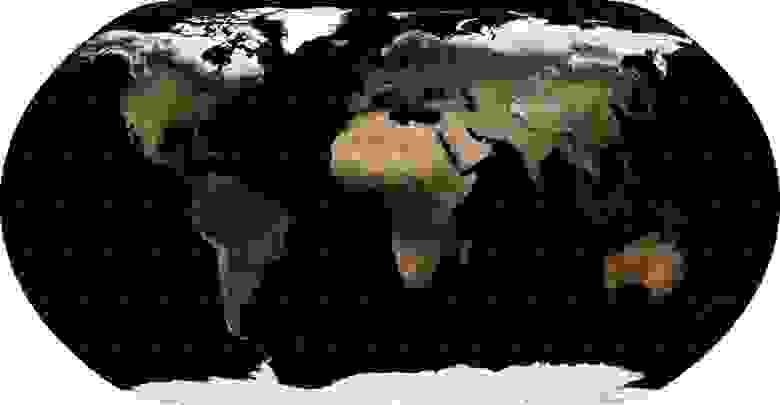
Тут стоит сделать небольшое отступление и обратить внимание на то, что вид этой проекции по умолчанию страдает одним недостатком, который касается и других общемировых проекций. Дело в том, что если за центральный меридиан — линию, соединяющую северный и южный полюс через центр карты (longitude of origin) — принять нулевой меридиан, то карта будет разрезана по 180-му. Но при этом треть Чукотки окажется на левом краю карты, а две трети — на правом. Чтобы сделать карту красивее, разрез должен проходить где-то в районе 169-го западного меридиана восточнее острова Ратманова, для чего за центральный должен быть принят 11-й. Вот иллюстрация того, что получается:
А вот измененное для этого случая описание в ESRI WKT:
PROJCS[«Robinson»,
GEOGCS[«GCS_WGS_1984»,
DATUM[«D_WGS84»,
SPHEROID[«WGS84»,6378137,298.257223563]
],
PRIMEM[«Greenwich»,0],
UNIT[«Degree»,0.017453292519943295]
],
PROJECTION[«Robinson»],
PARAMETER[«central_meridian»,11],
PARAMETER[«false_easting»,0],
PARAMETER[«false_northing»,0],
UNIT[«Meter»,1]
]
В формате определения системы координат для PROJ.4 долгота центра проекции задается параметром +lon_0=.
11-й меридиан — «магическое» число: практически все мировые проекции, имеющие равномерный масштаб вдоль экватора, могут быть разрезаны по Берингову проливу, если за центральный принять именно его, а не нулевой.
Замечу, что задумываясь о выборе проекции, стоит принимать во внимание все существующие реальные требования к визуализации. Например, если данные касаются климата, то может иметь смысл либо нанести на карту линии широты, либо использовать проекцию, где они горизонтальны, а не загибаются к краям карты (то есть, отказаться от Тройной Винкеля в пользу, например, Робинсона). В данном случае, это позволит легче и точнее оценить относительную близость разных мест к полюсам и экватору. Еще один весомый плюс проекции Робинсона — то, что она поддерживается множеством софта, в том числе открытого, тогда как про некоторые другие этого сказать нельзя.
Иногда, когда требуется максимально сохранить какое-то свойство, например — соотношение площадей объектов (стран) — эстетическая сторона страдает. Но поскольку это все же может для чего-то понадобиться, я приведу один пример такой проекции — «проекцию Моллвейде», Mollweide projection WKID:54009 PROJ.4:moll.
Как видно, она довольно сильно напоминает проекцию Робинсона, но с той разницей, что полюса все же стянуты в точки, от чего форма приполярных областей выглядит сильно искаженной. Но пропорции площадей стран, как и требовалось, сохраняются куда лучше.
Самым молодым конкурентом этих проекций является проекция Natural Earth PROJ.4:natearth — она представляет из себя гибрид проекций Каврайского и Робинсона, а ее параметры были подобраны группой американских, швейцарских и словенских специалистов в 2007 году, тогда как возраст большинства картографических проекций — не менее полувека.
Для перепроецирования данных в нее существует некоторое количество инструментов, которые были написаны специально для этого, но ее поддержка еще далека от повсеместной.
Немного экзотики и специальных случаев
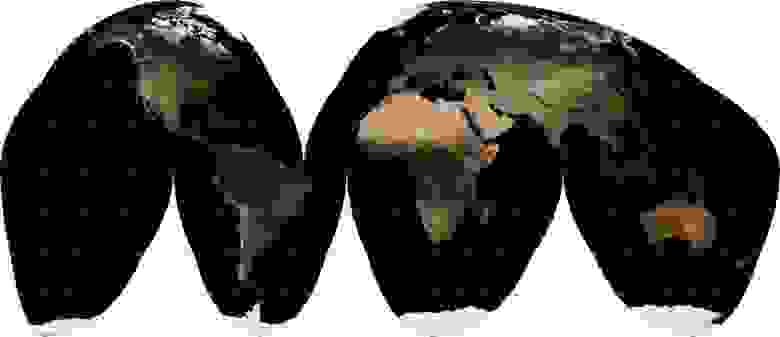
Конечно, все многообразие проекций на этом не заканчивается. Их изобретено немало. Некоторые просто выглядят странно (скажем, проекция Бонне изображает Землю в виде фигуры, напоминающей разрезанное яблоко или стилизованное сердце), некоторые — предназначены для особых ситуаций. Например, готов поспорить, что очень многие видели на картинках карту мира, которая похожа на корку мандарина, которую сняли и расплющили. Это, наверняка, была «Разрывная гомолосинусоидальная проекция Гуда» Interrupted Goode Homolosine projection WKID:54052.
Вид ее вполне достоин названия. Ее назначение — отображать размер объектов (и в некоторой степени — форму) близко к естественным пропорциям. Ее главная проблема, кроме названия и странного вида, состоит в том, что путем подбора центрального меридиана невозможно добиться того, чтобы ни один крупный кусок суши не был разрезан. Обязательно пострадает что-то из списка: Гренландия, Исландия, Чукотка, Аляска. Лично на мой взгляд, проще привести отдельно изображения стран, чем использовать такую карту, если вы не хотите стилизовать свою работу под середину XX века.
На иллюстрации эта проекция имеет широту и долготу центра, равные широте и долготе Москвы, а высоту — 5000000 метров. Чем больше это расстояние, тем сильнее изображение Земли становится похоже на ее изображение в проекции, которую мы рассмотрим последней.
Проекция, которая показывает вид на Землю в параллельной перспективе, то есть как-бы с бесконечного расстояния, называется «Ортографическая проекция» Orthographic projection WKID:43041 PROJ.4:ortho. В каком-то смысле, она знакома всем, кто когда-либо пользовался Google Earth. Я говорю, что в каком-то смысле, потому что «направление взгляда» в этой проекции всегда перпендикулярно поверхности Земли, тогда как в Google Earth его можно наклонять как угодно.
Для нее, как и для предыдущей проекции, можно задать центральные широту и долготу, чтобы ориентировать Землю желаемым образом. Например, можно показать полушарие с центром в какой-то точке, о которой идет речь — скажем, иллюстрируя транспортные потоки континентального масштаба, исходящие от одного предприятия. Сделав две карты с противоположными значениями координат, можно получить карту всего мира (правда, на краях искажения будут очень велики). Генерация последовательности карт с плавным изменением центральной точки даст кадры для анимации вращающейся планеты без всякой трехмерной графики.
Если статья окажется интересной, постараюсь написать продолжение о проекциях, используемых для отображения отдельных стран или регионов, ориентированную, как и эта статья, на базовые свойства этих проекций для задачи визуализации данных, инфографики и тому подобного.
GIS-LAB
Географические информационные системы и дистанционное зондирование
Краткое введение в ГИС. Часть 7: Системы координат
| ГИС для преподавателей | Часть 7: Системы Координат | |
 | Цель: Понимание систем координат | |
Ключевые слова: Система координат (СК), Картографическая Проекция, Проецирование «На лету», Широта, Долгота, Северное Смещение, Восточное Смещение
Картографические проекции служат для представления сферической поверхности Земли на плоскости бумажной или компьютерной карты. Системы координат (СК) определяют, как двумерная спроецированная карта описывает реальные местоположения на Земле с помощью координат. Выбор картографической проекции и системы координат зависит от географической области, которую Вы хотите показать на карте, от задач, стоящих перед будущей картой, и часто от доступности данных.
Подробнее о картографических проекциях:
Традиционный метод представления формы Земли – это глобус. Тем не менее, здесь возникает ряд проблем. Хотя глобусы достаточно точно передают форму Земли и очертания континентов, их невозможно носить с собой в кармане. Также они подходят для использования в очень малых масштабах (примерно 1 к 100 млн). Большинство тематических данных, используемых в картографических приложениях, имеют гораздо более крупный масштаб. Типичные наборы геоданных имеют масштаб 1:250 000 или крупнее, в зависимости от уровня детализации. Глобус подобного масштаба было бы трудно произвести и еще более трудно сдвинуть с места. Поэтому картографы разработали ряд математических техник, называемых картографическими проекциями, разработанных для представления сферической поверхности Земли в двух измерениях.
Смотря на Землю с близкого расстояния, люди воспринимают ее плоской. Тем не менее, из космоса она выглядит шарообразной. Карты, как известно, являются представлением реальности. Они создаются для представления не только самих объектов, но и их формы, размеров и пространственных отношений. Каждая картографическая проекция имеет достоинства и недостатки. Выбор лучшей проекции зависит от масштаба карты и от цели ее создания. Например, проекция, которая будет иметь неприемлемые искажения в случае создания карты на весь африканский континент, может быть отличным решением для составления крупномасштабной (детальной) карты одного из африканских городов. Свойства картографической проекции также воздействуют на визуальные характеристики карты. Некторые проекции хороши для малых областей, некоторые – для территорий с большим протяжением с запада на восток, третьи – с севера на юг.
Три семейства картографических проекций:
Процесс создания картографической проекции может быть наглядно показан путем помещения источника света внутрь прозрачного глобуса с обозначенными параллелями и меридианами. Свет падает на лист бумаги. Различные способы проецирования имитируются оборачиванием глобуса листом в форме цилиндра, конуса, или просто прикладыванием плоского листа. Каждый из этих методов называется семейством картографических проекций. Таким образом, существуют семейства цилиндрических, конических и плоскостных проекций (см. Рисунок 62а, б, в).
Рисунок 62: Три семейства картографических проекций: а) цилиндрические, б) конические и в) плоскостные проекции
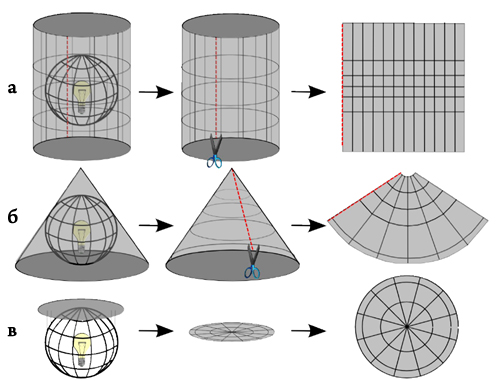
Процесс проецирования осуществляется с использованием математических принципов геометрии и тригонометрии. Процесс, показанный выше, моделируется числовыми функциями.
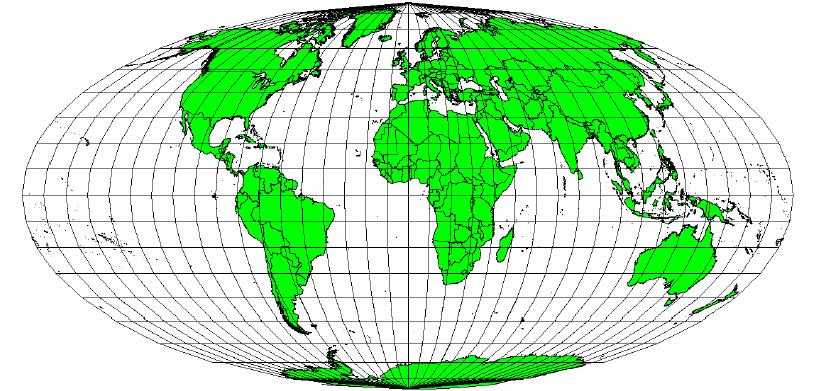
Точность картографических проекций
Картографические проекции по определению не могут передать сферическую поверхность со 100% точностью. В ходе проецирования любая карта будет иметь искажения углов, расстояний или площадей. Картографическая проекция может быть компромиссной, т.е. искажать все три свойства в некоторых допустимых пределах. Примером компромиссной проекции служит проекция Робинсона (см. Рисунок 63), часто используемая для карт мира.
Рисунок 63: Проекция Робинсона является компромиссной проекцией, в которой искажения
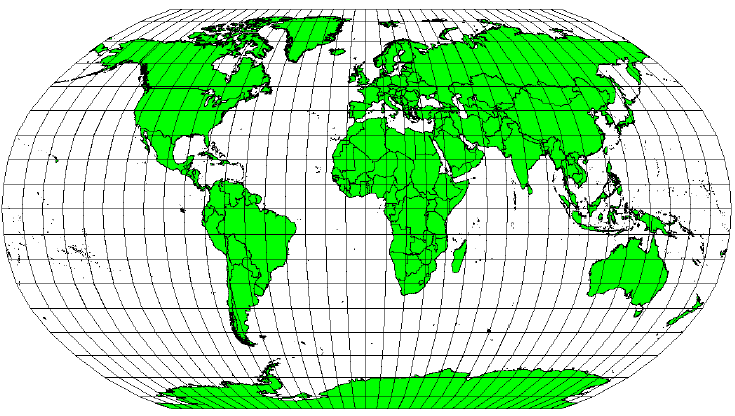
площадей, углов и расстояний находятся на приемлемом уровне.
Как уже сказано, при перенесении Земли на плоскость сохранить точность всех характеристик одновременно невозможно. Это означает, что если Вам нужно осуществлять точные аналитические операции по карте, Вы должны выбрать картографическую проекцию, которая наилучшим образом сохраняет точность характеристики, которую Вы будете измерять. Например, если Вы хотите измерять расстояния на Вашей карте, Вам следует выбрать проекцию, которая обеспечивает высокую точность расстояний.
Равноугольные картографические проекции
На глобусе главные направления розы ветров (север, запад, юг и восток) всегда находятся под углом 90 градусов друг к другу. Другими словами, меридианы всегда находятся под прямым углом к параллелям. Такие углы могут быть сохранены на картографической проекции, называемой равноугольной. Также такая проекция называется конформной, или ортоморфической.
Рисунок 64: Проекция Меркатора используется в случаях, когда важно сохранить углы.
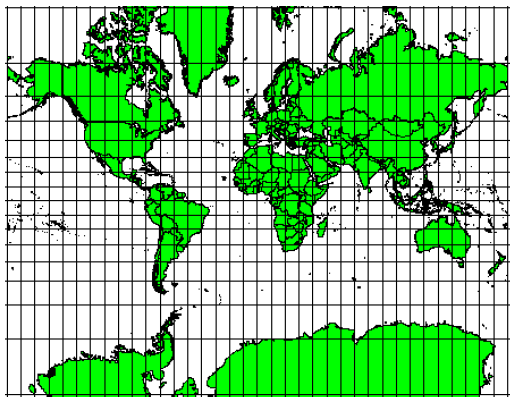
В то же время, она сильно искажает площади в высоких широтах.
Подобные проекции используются, когда важно сохранить правильные углы, в частности для навигационных и метеорологических задач. Важно помнить, что сохранение правильных углов на карте ведет к искажению других характеристик и действительно на малых площадях. Так, конформная проекция искажает площади, т.е. если на карте с конформной проекцией будут измерены площади, их значения будут неправильными. Чем больше область, изображенная на карте, тем больше будут искажены площади. Примеры конформных проекций – Проекция Меркатора (см. Рисунок 64) и Конформная Коническая Проекция Ламберта. Подобные проекции используются на многих картах Геологической Службы США.
Если Вы хотите правильно измерять расстояния, Вам потребуется картографическая проекция, которая хорошо сохраняет расстояния. Такие проекции, называемые равнопромежуточными, поддерживают постоянный масштаб карты. Карта является равнопромежуточной, когда она корректно отображает расстояния от центра проекции до любой другой точки на карте. Равнопромежуточные проекции обеспечивают правильные расстояния от центра проекции вдоль определенных линий. Эти проекции используются для сейсмического картографирования, а также для задач навигации. Цилиндрическая Проекция Плате-Карре (см. Рисунок 65) и Равнопромежуточная проекция относятся к этому типу проекций. Есть и другие проекции, например Азимутальная Равнопромежуточная Проекция используется на эмблеме ООН (см. Рисунок 66).
Рисунок 65: Проекция Плате-Карре используется, когда важно правильное измерение расстояний.
Рисунок 66: На логотипе ООН используется азимутальная равнопромежуточная проекция.
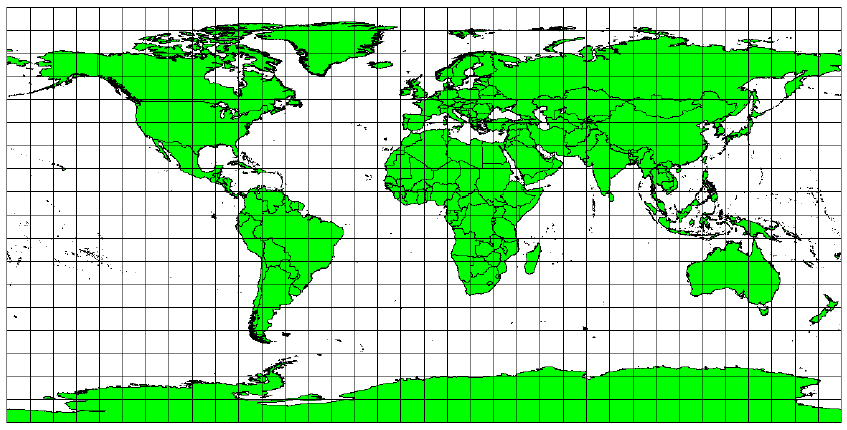
Когда площади объектов на карте имеют те же пропорциональные отношения, что и площади объектов на Земле, это означает, что использована равновеликая проекция. Такие проекции широко используют на картах общего назначения, а также на образовательных картах. Как подсказывает название, эти карты лучше всего подходят для расчетов площадей. Например, если Вам нужно проанализировать конкретный район города, чтобы определить, достаточно ли там свободного места для нового супермаркета, лучшим выбором для карты будет равновеликая проекция. С одной стороны, чем больше будет территория покрытия Вашей карты, тем более точными будут Ваши измерения площадей в случае использования равновеликой проекции по сравнению с другими типами. С другой стороны, равновеликая проекция приводит к искажению углов при больших территориях охвата. На малых площадях искажения углов будут незначительными. Примеры равновеликих проекций, часто используемых в ГИС: Равновеликая Проекция Альберса, Равновеликая Проекция Ламберта и Равновеликая Цилиндрическая Проекция Мольвейде (см. Рисунок 67).
Помните, что картографические проекции – это очень сложная тема. Существуют сотни различных проекций, каждая из которых подходит для определенных территорий и задач. Чаще всего выбор правильной проекции лежит на ГИС-специалисте. Во многих странах есть свои популярные проекции, и в случае обмена данными люди просто следуют национальным тенденциям.
Рисунок 67: Равновеликая Цилиндрическая Проекция Мольвейде обеспечивает правильные пропорции площадей.
Подробнее о системах координат (СК)
С помощью систем координат (СК) каждое место на Земле может быть описано набором из трех цифр, называемых координатами. В общем, СК делят на системы географических координат и системы проекционных координат (также называются картезианскими, или прямоугольными).
Системы Географических Координат
Использование географических координат широко распространено. Системы географических координат основаны на широте и долготе, а также дополнительном значении высоты для описания местоположений на Земле. Самая популярная в наше время называется WGS 84.
Рисунок 68: Система географических координат, состоящая из параллелей и меридианов.
Линии долготы (меридианы), с другой стороны, не являются регулярными. Они пересекают экватор под прямым углом, а потом сходятся на полюсах. Линия нулевой долготы (нулевой меридиан) идет от Северного полюса к Южному полюсу через Гринвич, Англия. Долгота измеряется от 0 до 180 градусов к западу или востоку от нулевого меридиана. Стоит заметить, что в ГИС-приложениях значения к западу от нулевого меридиана имеют негативные значения (см. Рисунок 68).
На экваторе, и только на экваторе, расстояние между соседними меридианами, равно расстоянию между соседними параллелями. По мере приближения к полюсам, расстояние между меридианами уменьшается до тех пор, пока все 360 градусов долготы не сходятся в одной-единственной точке полюса. Используя систему географических координат, мы имеем сетку линий, разделяющую Землю на фигуры, покрывающие примерно 12363.365 кв. км на экваторе. хорошее начало, но не очень полезное для точного определения местоположения.
Чтобы быть по-настоящему полезной, градусная сетка делится на более мелкие участки, которые способны определить местоположение объекта с допустимым уровнем точности. Для этого градусы разделены на минуты (‘) и секунды («). В градусе 60 минут, в минуте 60 секунд, соответственно в градусе 3600 секунд. Значит, на экваторе одна секунда широты или долготы примерно равна 30.87624 м
Системы проекционных координат
Двумерная координатная система обычно определяется двумя осями. Располагаясь под прямым углом друг к другу, они формируют так называемую XY-плоскость (см. Рисунок 69, слева). Горизонтальная ось обычно подписывается как X, вертикальная – как Y. В случае трехмерной системы координат добавляется третья ось Z. Она также располагается под прямым углом к двум первым осям (см. Рисунок 69, справа). Представьте себе, что внутри этой системы расположена сфера. Каждая точка на этой сфере, имеющая сферические координаты, может быть выражена в координатах XYZ.
Рисунок 69: Система проекционных координат. Двумерная система с координатами X и Y (слева) и трехмерная система с координатами X, Y и Z (справа).
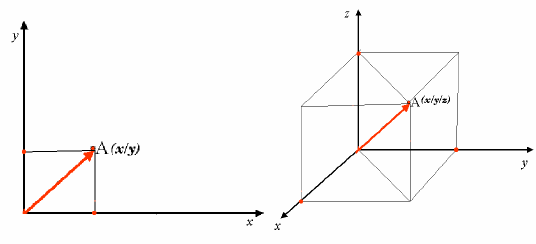
Система проекционных координат в Южном полушарии (к югу от экватора) берет отсчет на экваторе от определенной долготы. Это значит, что значения Y повышаются на юг, а значения X растут в сторону запада. В Северном полушарии (к северу от экватора) проекционная СК также берет начало от экватора на определенной долготе. При этом значения Y растут в сторону севера, а значения X увеличиваются на восток. Дальше мы опишем систему проекционных координат, называемую Универсальной Поперечной Проекцией Меркатора (UTM), часто используемую для территории ЮАР.
Подробнее об Универсальной Поперечной Проекции Меркатора
Точка отсчета системы координат UTM находится на экваторе на определенной долготе. Значения Y повышаются на юг, а значения X растут в сторону запада. UTM является глобальной картографической проекцией. Это означает, что она используется по всему миру. Но, как описано выше, с увеличением площади использования растет степень искажения геометрических параметров. Для того, чтобы избежать повышения искажений, Землю поделили на 60 одинаковых зон, каждая из которых занимает 6 градусов долготы. Зоны UTM пронумерованы от 1 до 60, и номера растут с запада на восток. Нумерация начинается от линии перемены дат (зона 1 находится на 180 градусах Западной долготы) и увеличивается на восток (зона 60 примыкает к 180 градусами Восточной долготы), как показано на Рисунке 70.
Рисунок 70: Зоны Универсальной Поперечной Проекции Меркатора. Для Южной Африки используются зоны 33S, 34S, 35S и 36S.
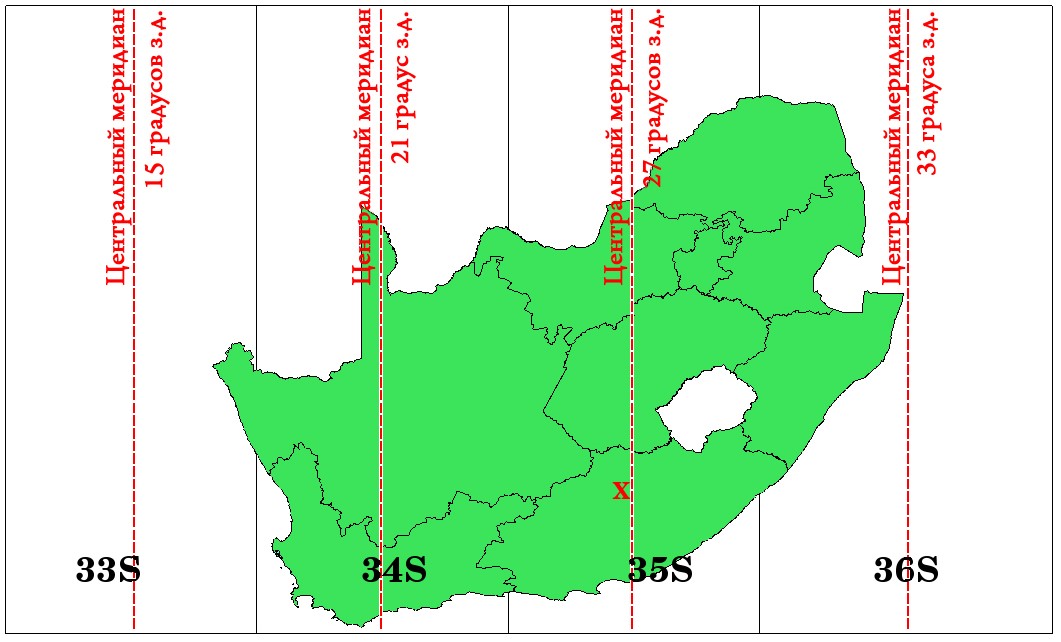
Как можно видеть на Рисунках 70 и 71, Южная Африка покрыта четырьмя зонами UTM для минимизации искажений. Зоны называются 33S, 34S, 35S и 36S. Буква S после зоны означает положение к югу от экватора.
Рисунок 71: Зоны 33S, 34S, 35S и 36S, используемые для высокоточного проецирования территории ЮАР, и их центральные меридианы.
Красным крестом помечена область интереса.
Например, мы хотим определить координаты в области интереса, помеченной красным крестиком на Рисунке 71. Как Вы можете видеть, область находится в зоне 35S. Это означает: для того, чтобы минимизировать искажения и получить корректный результат, нужно использовать UTM, зону 35S в качестве системы координат. Позиция координаты в системе UTM к югу от экватора описывается номером зоны (35) и северным (y) и восточным (x) смещением. Северное смещение – это расстояние от экватора в метрах. Восточное смещение – это расстояние от центрального меридиана используемой зоны UTM. Для зоны 35S центральный меридиан проходит по линии 27° в.д., как показано на Рисунке 71. Кроме того, в UTM используются только положительные значения, потому ко всем значениям y прибавляют 10 000 000 м, а ко всем значениям х прибавляют 500 000 м. Это может показаться трудным, поэтому мы проиллюстрируем на примере, как найти правильную координату для области интереса в системе UTM 35S.
Северное смещение (y)
Восточное смещение (х)
В результате, координата для нашей точки интереса (POI), проецированная в системе UTM 35S, будет записываться как 35 415000 mE / 6450000mN. В некоторых ГИС, когда определена правильная зона и единицы измерения карты установлены на метры, координаты могут отображаться просто как 415000; 6450000.
Как Вы могли уже подумать, довольно распространены ситуации, когда данные, которые Вы хотите использовать в ГИС, находятся в разных системах координат. Например, у Вас может быть векторный слой границ в проекции UTM 35S и точечный слой с метеорологической информацией, записанный в географической системе WGS84. Если открыть эти слои в ГИС, мы увидим, что они отображаются в абсолютно разных местах, хотя по факту информация относится к одной и той же территории.
Для решения этой проблемы многие ГИС имеют функцию, называемую проекцией «на лету». Это значит, что Вы можете задать определенную проекцию вашей карты перед тем, как добавлять слои, а затем по мере добавления слоев они будут автоматически отображаться в заданной проекции, вне зависимости от того, в какой проекции они записаны изначально. Эта функция обеспечивает корректное наложение слоев даже в случае различающихся систем координат.
О чем стоит помнить:
Тема картографических проекций очень сложна, и даже профессионалы в области географии, геодезии и ГИС часто испытывают проблемы при ответе на вопрос, что такое картографические проекции и системы координат. Обычно, когда Вы работаете в ГИС, данные уже находятся в определенной проекции, так что Вам не понадобится определять проекцию. Более того, благодаря функции проецирования «на лету» часто нет необходимости перепроецировать данные. Тем не менее, всегда полезно знать, что означают эти термины.
Закрепим изученный материал:
Ниже приведено несколько примеров практических заданий для Ваших учеников:
Если у Вас нет компьютера:
Вы можете показать Вашим ученикам принципы трех семейств картографических проекций. Возьмите глобус и карту и продемонстрируйте общие принципы работы цилиндрических, конических и плоскостных проекций. С помощью кальки Вы можете нарисовать двумерную систему координат, состоящую из осей X и Y. Затем, позвольте Вашим ученикам определить координаты для различных мест.
Руководство пользователя QGIS также содержит более детальную информацию о работе с картографическими проекциями в QGIS.
В следующем разделе мы познакомимся с подготовкой карт.
Последнее обновление: 2014-05-14 23:50
Дата создания: 09.08.2013
Автор(ы): Алексей Еськов