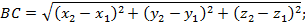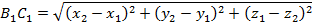что такое зеркальная симметрия

Зеркальная симметрия: определение и примеры

Какие примеры зеркальной симметрии можно встретить в повседневном мире и всегда ли это красиво? Что это такое? Какие характеристики ее определяют? Отражательную симметрию можно найти в геометрических фигурах, математике, природе и искусственном мире.

Что такое рефлексивная симметрия?

Какое можно дать определение? Зеркальная симметрия возникает, если при разделении объекта или формы пополам, каждая половина будет отражать другую. Иногда объекты или формы имеют более одной линии симметрии. Возьмем, к примеру, букву H. Сколько линий симметрии она имеет? Если вы ответили две, вы правы. Есть два способа сделать линию, чтобы каждая половина отражала другую половину.

Можно ли считать человеческое лицо симметричным?

Однако, поскольку люди имеют неконтролируемые различия, наши лица не всегда могут рассматриваться как идеальные примеры. Например, у некоторых из нас может быть одна сторона лица красивее, чем вторая. Если вы внимательно посмотрите в зеркало, вы можете заметить, что один из ваших глаз немного меньше другого, одна скула шире, чем другая, и так далее. Многие аспекты человеческого облика могут искажать понятие истинной рефлексивной симметрии, поэтому истинная зеркальная симметрия должна удовлетворять определенным условиям.

Примеры рефлексивной симметрии

Многие буквы алфавита имеют зеркальную симметрию. Некоторые используют вертикальную линию; некоторые используют горизонтальную линию. Какие есть примеры зеркальной симметрии в геометрии? Формы также могут демонстрировать рефлексивную симметрию, такую ​​как круги и квадраты, которые имеют четыре линии симметрии. В зависимости от типа треугольника можно иметь нулевую, одну или три линии.

Поскольку мы все больше и больше изучаем нашу окружающую среду и наше окружение, мы видим, что природа может быть описана математически. Красота цветка, величие дерева, даже скалы могут проявлять зеркальную симметрию в природе. Есть и другие примеры, которые можно найти в кристаллографии или даже на микроскопическом уровне. Кажется, что везде, куда мы сейчас смотрим, наши глаза сначала обращаются к существующим образцам симметрии.

Существуют разные виды симметрии

В математике

В природе

Многие животные являются симметричными. Такие организмы имеют отражательную симметрию в сагиттальной плоскости, которая разделяет тело вертикально на левую и правую половинки с одним из каждого органа чувств и пары конечностей с обеих сторон. Большинство животных имеют двустороннюю симметричность, вероятно, потому что это поддерживает движение вперед и баланс.

В архитектуре

Симметрия помогает связать различные элементы структуры вместе в единое целое. Она также широко используется для создания чувства рационального порядка и спокойной логики, предпочтительной эстетики древних греков и римлян. Мы можем смотреть на симметрию во многих масштабах, от отношения между отдельными деталями, до макета полной структуры и даже до всех городских центров, построенных на симметричной сетке.

Основополагающий принцип устройства мира

Симметрия – везде, и поэтому она является эффективным методом познания природы. В природе она обеспечивает устойчивость, равновесие, надежность и прочность. Симметричные формы более устойчивы к различным воздействиям. Существует бесчисленное множество видов симметрии, однако, для живой и неживой природы также является вполне естественной определенная асимметрия.

Для организации всех живых структур свойственно геометрическое подобие. например, кленовые листочки похожи друг на друга, лист березы подобен листу березы и так далее. Что бы ни происходило в процессе жизнедеятельности живой клетки, которая принадлежит целому организму и выполняет функцию его воспроизведения в новый отдельный субъект, она является все лишь отправной точкой. В результате деления эта маленькая ячейка преображается и формируется в объект, схожий по всем показателям первоначальному.

Живым организмам симметрия оказывает неоценимую услугу, в первую очередь, это равновесие при передвижении и функционировании. Это можно наблюдать и в растительном мире. Симметричное расположение ветвей обеспечивает стволам деревьев определенную устойчивость тем, что регулирует распределение силы тяжести. Интересен то факт, что большинство деревьев и имеют конусообразную вершину. С чем это связано? Все в природе хорошо продумано: форма конуса дает возможность не только верхним, но и нижним листьям получать достаточное количество солнечных лучей, не говоря уже об установлении центра тяжести, от которого зависит устойчивость растения.

Симметрия вместе с асимметрией успешно сосуществуют в нашем мире, и та и другая нашли свое отражение в генах живых организмов, они гармонично дополняют друг друга.

Источник

Зеркальная симметрия

Отражение, зеркальное отражение или зеркальная симметрия — движение евклидова пространства, множество неподвижных точек которого является гиперплоскостью (в случае трехмерного пространства — просто плоскостью).

Термин зеркальная симметрия употребляется также для описания соответствующего типа симметрии объекта, т.е., когда объект при операции отражения переходят в себя.

Это математическое понятие описывает соотношение в оптике объектов и их (мнимых) изображений при отражении в плоском зеркале, а также многие законы симметрии (в кристаллографии, химии, физике, биологии и т. д., а также в искусстве и искусствоведении)

Осевая симметрия

В размерности 2 (то есть на плоскости) гиперплоскость представляет собой прямую, говорят об осевой симметрии или симметрии относительно прямой.

Для фигуры, переходящей в себя при осевой симметрии, прямая, образованная неподвижными точками движения, называется осью симметрии этой фигуры. Примером оси симметрии отрезка является его серединный перпендикуляр.

Любое движение плоскости можно представить в виде композиции не более чем трёх осевых симметрий.

См. также

Полезное

Смотреть что такое «Зеркальная симметрия» в других словарях:

ЗЕРКАЛЬНАЯ СИММЕТРИЯ — в физике частиц симметрия относительно пространственной инверсии. Нарушается в процессах слабого взаимодействия. Физическая энциклопедия. В 5 ти томах. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988 … Физическая энциклопедия

зеркальная симметрия — ▲ симметрия ↑ относительно, плоскость зеркальная симметрия равноудаленность соответственных точек двух фигур от соответственных сторон оси или плоскости; одинаковость положения двух фигур относительно оси или плоскости. билатеральность.… … Идеографический словарь русского языка

зеркальная симметрия — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN mirror symmetry … Справочник технического переводчика

зеркальная симметрия — veidrodinė simetrija statusas T sritis fizika atitikmenys: angl. bilateral symmetry; mirror symmetry; specular symmetry vok. Spiegelsymmetrie, f rus. зеркальная симметрия, f pranc. symétrie par réflexion, f … Fizikos terminų žodynas

СИММЕТРИЯ — (от греч. соразмерность), понятие, характеризующее переход объектов в самих себя или друг в друга при осуществлении над ними оп редел. преобразований (преобразований С.); в широком смысле свойство неизменности (инвариантности) некоторых… … Философская энциклопедия

СИММЕТРИЯ — (от греч. symmetria соразмерность) законов физики. Если законы, устанавливающие соотношение между величинами, характеризующими физ. систему, или определяющие изменение этих величин со временем, не меняются при определённых операциях… … Физическая энциклопедия

Симметрия (физика) — У этого термина существуют и другие значения, см. Симметрия (значения). Симметрия в физике Преобразование Соответствующая инвариантность Соответствующий закон сохранения ↕ Трансляции времени …энергии ⊠ C, P, CP и T симметрии …чётности ↔… … Википедия

симметрия — ▲ одинаковость ↑ расположение, несколько, фигура, относительно, центр (фигуры) < > асимметрия, асимметричный. асимметрический. несимметричный. симметрия одинаковость расположения фигур вокруг условного центра (одинаковые расстояния их… … Идеографический словарь русского языка

Симметрия (в физике) — Симметрия в физике. Если законы, устанавливающие соотношения между величинами, характеризующими физическую систему, или определяющие изменение этих величин со временем, не меняются при определённых операциях (преобразованиях), которым может быть… … Большая советская энциклопедия

СИММЕТРИЯ МОЛЕКУЛЫ — хар ка молекулы, определяемая совокупностью возможных операций точечной симметрии для её равновесной конфигурации. Четыре операции точечной симметрии (вращение вокруг оси на нек рый угол, меньший или равный 360°; отражение от плоскости; инверсия… … Физическая энциклопедия

Источник

Презентация по геометрии «Зеркальная симметрия» (11 класс)

Описание презентации по отдельным слайдам:

Описание слайда:

Описание слайда:

Что такое симметрия?
Симметрия — это соразмерность, пропорциональность частей чего-либо, расположенных по обе стороны от центра. Говоря проще, если обе части от центра одинаковы, то это симметрия.
Зеркальной симметрией (относительно плоскости) называется такое отображение пространства на себя, при котором любая точка переходит в симметричную ей относительно плоскости точку.

Описание слайда:

Как нужно написать слово РЕАНИМАЦИЯ на капоте машины скорой помощи, чтобы водитель впереди едущей машины увидел в зеркале верную надпись?

Описание слайда:

Решение:
написать нужно следующим образом
Почему так? Потому что в зеркале все видится симметрично.
Если отразить эту надпись, то в зеркале водитель впереди едущей машины видит РЕАНИМАЦИЯ. И сразу пропустит такой автомобиль.

Описание слайда:

Симметрично ли наше лицо?
Человек, многие животные, рыбы и насекомые практически зеркально симметричны. Почему «практически»? Судите сами на примере человека: строение внутренних органов у человека не симметричное, зато внешне, руки, ноги, глаза, уши и т.д. человек симметричен.
Так симметрично ли наше лицо? Сейчас в Интернете можно найти много изображений, которые сделаны так: взята левая половинка лица, которая отражена симметрично направо в компьютерной программе, а потом аналогично с правой. Смотрите, что получается.

Описание слайда:

Пример задачи
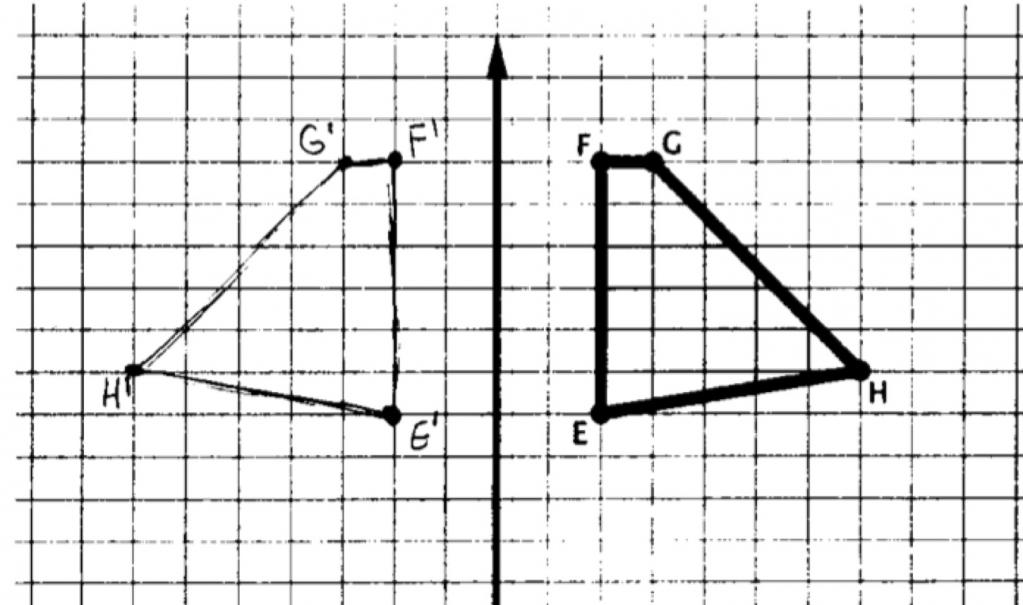
Постройте зеркальную симметрию тетраэдра, относительно плоскости L, изображенных на рисунке 1.
Для построения такой зеркальной симметрии сначала проведем через все точки тетраэдра прямые, каждая из которых будет перпендикулярна к плоскости l (рисунок 2).
Далее, для построения будем использовать определение.

Рисунок 1.
Рисунок 2.

Описание слайда:

Точки P и P′ будем называть симметричными относительно какой-либо плоскости a, если прямая (PP′) будет перпендикулярна плоскости a и, при этом, плоскость a будет делить отрезок [PP′] пополам.

Описание слайда:

Пример задачи
4. Точка A перейдет в такую точку A′, которая будет принадлежать прямой a.
Точка B перейдет в такую точку B′, которая будет принадлежать прямой b.
Точка C перейдет в такую точку C′, которая будет принадлежать прямой c. Аналогично, и точка D перейдет в такую точку D′, которая будет принадлежать прямой d. Причем, при этом первоначальная плоскость l делит отрезки AA′, BB′, CC′, DD′ пополам. Зеркальная симметрия этого тетраэдра изображена на рисунке.

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Ищем педагогов в команду «Инфоурок»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

также Вы можете выбрать тип материала:

Общая информация

Похожие материалы

Презентация к уроку геометрии в 8 классе по теме «Осевая и центральная симметрия»

Внеклассное мероприятие на тему «Пресс-конференция» по математике (8 класс)

Презентация по геометрии на тему «медианы, биссектрисы и высоты треугольника»(9 класс)

Краткосрочные планы.признаки равенства треугольников

Подборка 16 заданий ОГЭ по математике (окружность)

Презентация «Многогранники. Призма и ее мвойства.»

Практическое задание по теме «Осевая симметрия».

Практическое задание по теме «Параллельный перенос»

Не нашли то что искали?

Воспользуйтесь поиском по нашей базе из
5327405 материалов.

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Минобрнауки учредит именные стипендии для студентов из малочисленных народов

Время чтения: 1 минута

Путин поручил не считать выплаты за классное руководство в средней зарплате

Время чтения: 1 минута

В МГУ разрабатывают школьные учебники с дополненной реальностью

Время чтения: 2 минуты

Кузнецова призвала разработать закон о психологической помощи

Время чтения: 1 минута

В России зарегистрировали вакцину от коронавируса для подростков

Время чтения: 1 минута

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Чёрная пятница

На все курсы повышения квалификации и профессиональной переподготовки

Источник

Тема: Центральная и зеркальная симметрия

Выполнила ученица 11 А класса Ковалева Дарья

Учитель Багирян Нонна Александровна

· определение и основные свойства

· фигуры, обладающие центральной симметрией

· применение в жизни

· определение и построение

· фигуры, обладающие зеркальной симметрией

· зеркальная симметрия в реальной жизни

Другие названия этого преобразования — симметрия с центром A. Центральная симметрия в планиметрии является частным случаем поворота, точнее, является поворотом на 180 градусов.

· Центральная симметрия является движением;

· Любая прямая при центральной симметрии преобразуется в прямую. Причем, прямая, проходящая через центр, преобразуется в себя. Прямая, не проходящая через центр, преобразуется в параллельную ей прямую. (доказано в задаче 2)

· Центральная симметрия сохраняет расстояния между точками.

· Центральная симметрия переводит отрезки в отрезки, лучи в лучи.

Докажем, что центральная симметрия является движением.

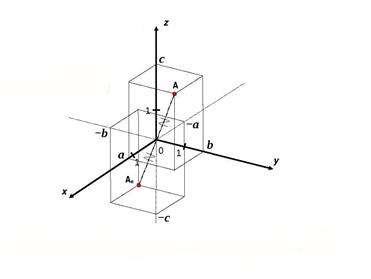
Обозначим буквой O центр симметрии и введем в прямоугольную систему координат Oxyz с началом в точке О. Установим связь между координатами двух точек M (x; y; z) и M₁ (x₁; y₁; z₁), симметричных относительно точки О.

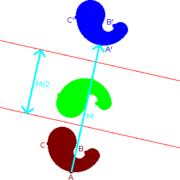
Построим точку А₀ симметричную точке А относительно точки О.

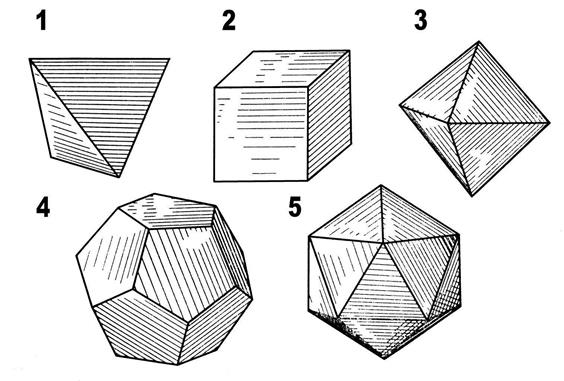
Фигуры, обладающие центральной симметрией.

1. – тетраэдр 2. – куб 3. – октаэдр 4. – додекаэдр 5. – икосаэдр

Применение центральной симметрии в жизни.

В архитектуре центральная симметрия используется реже осевой. Она присуща античным круглым храмам, используется в колоннах.

Колизей Пирамиды в Египте

Башни церквей, замков, колонны проектировались с учетом центральной симметрии. Такие сооружения предавали зданиям массивности. Башни одинаково роскошно выглядели с любой плоскости города.

Центральная симметрия в природе. Она присутствует в снежинках, листьях деревьев и трав, насекомых, цветах, животных.

Центральная симметрия прослеживается в

костюмах казанских татар

При центральной симметрии относительно начала координат знаки координат искомых точек меняются на противоположные.

№ 2. Докажите, что при центральной симметрии: а) прямая, не проходящая через центр симметрии, отображается на параллельную ей прямую; б) прямая, проходящая через центр симметрии, отображается на себя.

а)

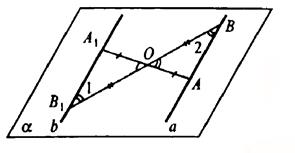
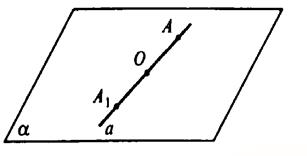
Через центр симметрии и данную прямую можно провести единственную плоскость. Пусть О — центр симметрии, а — данная прямая, α — плоскость, проведенная через О и а. Пусть А ∈ а, построим отрезок ОА.

Продолжим ОА за точку О на расстояние ОА₁=АО. Получим точку А₁, симметричную А.

Пусть В ∈ а, построим отрезок ОВ. Продолжим ОВ за точку О на расстояние ОВ₁=ОВ. Получим точку B₁, симметричную точке В.

Через А₁ и В₁ проведем прямую b. Рассмотрим ΔAОВ и ΔА₁ОВ₁⋅AО=А₁О, ВО=ОВ₁, ΔАОВ=ΔА₁ОВ₁ как вертикальные, следовательно, ΔAОВ=ΔА₁ОВ₁.

Пусть А ∈ а. Симметричная ей точка А₁ тоже принадлежит прямой а; АО=ОА₁.

Точка А произвольна, следовательно, любая точка прямой, а также симметричная точка относительно центра О лежат на прямой а, следовательно, прямая а переходит сама в себя при условии, что проходит через центр симметрии.

Зеркальной симметрией (симметрией относительно плоскости α) называется такое отображение пространства на себя, при котором любая точка М переходит в симметричную ей точку М₁ относительно плоскости α.

Докажем, что зеркальная симметрия является движением.

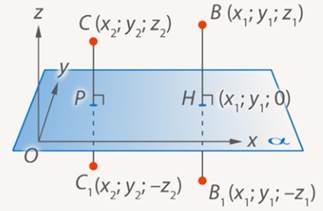
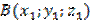
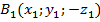
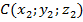
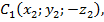
Для этого введем прямоугольную систему координат Оxyz так, чтобы плоскость Oxy совпала с плоскостью симметрии, и установим связь между координатами точек и , и симметричных относительно плоскости Oxy

Найдем длину отрезков BC и B₁C₁ по формуле расстояния между точками:

Отсюда BC = B₁C₁, значит, зеркальная симметрия является движением.

Отсюда следует, что зеркальная симметрия обладает следующими свойствами:

· переводит прямые в прямые

· полупрямые – в полупрямые

· отрезки – в отрезки

· плоскости – в плоскости

· сохраняет углы между прямыми.

Фигуры, обладающие зеркальной симметрией

(слева на право) – куб, пирамида, цилиндр, конус, сфера

Зеркальная симметрия в жизни

Наиболее распространена вархитектуре зеркальная симметрия.

Эйфелева башня Тадж Махал

Зеркальная симметрия в природе может быть представлена отражением изображения в воде.

Животные, растения, и человек тоже могут послужить примерами зеркальной симметрии. Однако назвать их идеальными примерами сложно, ведь даже лицо человека, которое на первый взгляд может показаться симметричным, таковым не является.

Аналогично решение с другими плоскостями.

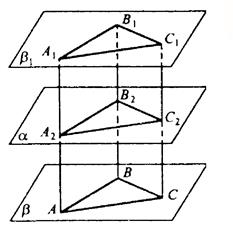
№ 2. При зеркальной симметрии относительно плоскости α плоскость β отображается на плоскость β₁. Докажите, что если: а) β || α, то β₁ || α; б) β ┴ α, то β₁ совпадает с β.

а) Выберем три точки в плоскости А, В, С, не лежащие на одной прямой. Проведем АА₂⊥α, ВВ₂ ⊥α, СС₂ ⊥α. Продолжим эти отрезки за точки А₁, B₁, C₁ так, что А₂А₁=АА₂, B₂B₁=BB₂, C₂C₁=CC₂.

Плоскость β₁ проходит через точки А₁, В₁ и C₁, она — единственная.

Если две пересекающиеся прямые (ВА и ВС) одной плоскости (β) параллельны двум прямым (B₁A₁ и В₁С₁) другой плоскости (β₁), то эти плоскости параллельны: β₁ || β.

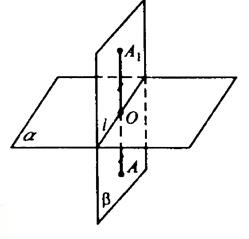
б)

Пусть α⊥β. Возьмем произвольную точку А ∈ β и построим АО перпендикулярно плоскости α. Продолжим отрезок за точку О на расстояние ОА₁=АО.

Две плоскости взаимно перпендикулярны и к одной из них проведен перпендикуляр, имеющий общую точку с другой плоскостью, тогда этот перпендикуляр весь лежит в этой плоскости, т.е.

АО⊂β, следовательно, и АА₁ ⊂β.

Таким образом, каждая точка плоскости β отображается в точку, ей симметричную, которая тоже принадлежит плоскости β. тогда, плоскость β отображается сама на себя, или β₁ совпадает с β.

Источник