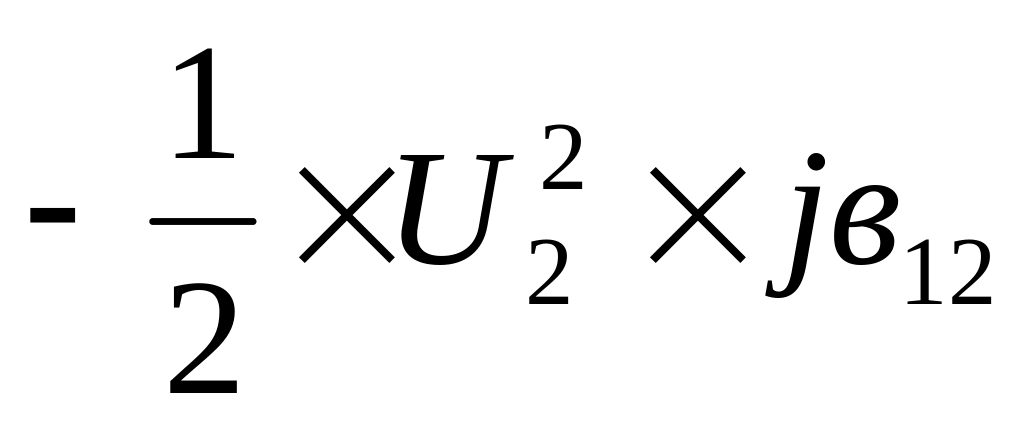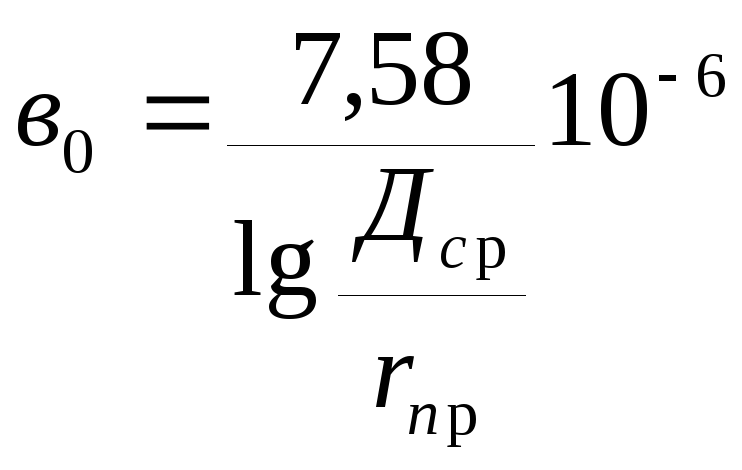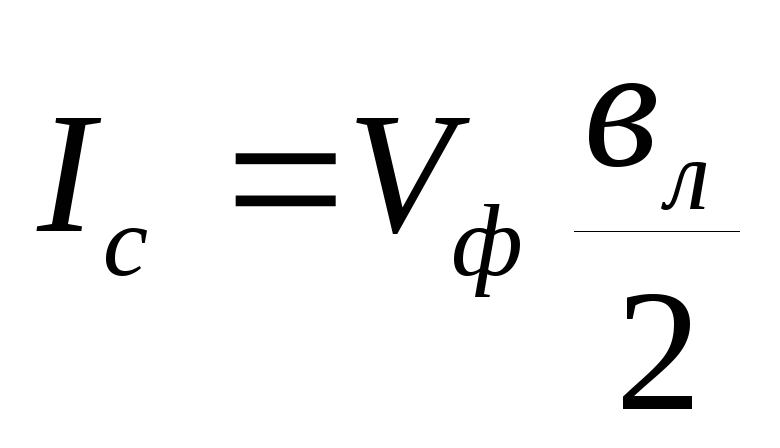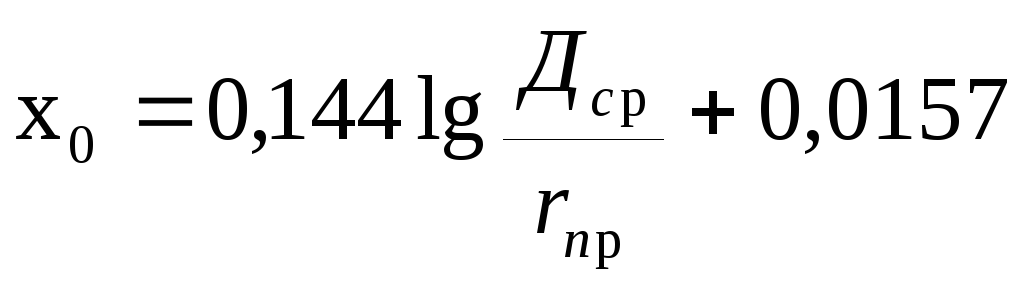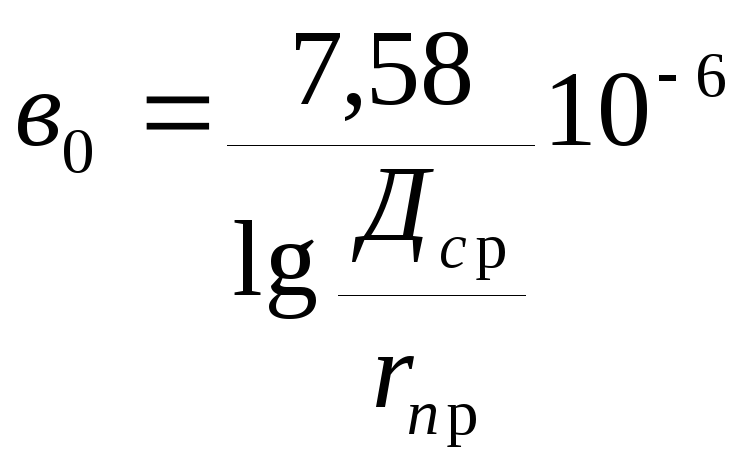что такое зарядная мощность линии это

Большая Энциклопедия Нефти и Газа

Зарядная мощность линии не зависит от ее нагрузки. Реактивная индуктивная мощность, потребляемая линией, пропорциональна квадрату тока, протекающего по ней. При определенном значении нагрузки потребителей эти мощности станут равными, и так как зарядная мощность протекает навстречу реактивной индуктивной мощности, они взаимно скомпенсируются. [1]

Зарядная мощность линии с номинальным напряжением 110 кВ ( рис. 3.9, а) составляет Qcno 3 Мвар. [2]

Требуется определить зарядную мощность линии Qb напряжение в начале линии и необходимое число включенных генераторов. [4]

Из-за большой величины зарядной мощности линий сверхвысокого напряжения для дальних передач является обязательным применение поперечных реакторов, что является радикальным средством для снижения передачи реактивной мощности по линии и связанных с ней потерь энергии в режимах малых нагрузок. Мвар на передаваемый 1 МВт активной мощности. [5]

Необходимость учета емкости и зарядной мощности линии зависит от соиз-меряемости зарядной и нагрузочной мощности. В местных сетях небольшой протяженности при номинальных напряжениях до 35 кВ зарядные токи и мощности значительно меньше нагрузочных. Поэтому в КЛ емкостную проводимость учитывают только при напряжениях 20 и 35 кВ, а в ВЛ ею можно пренебречь. [9]

Физически это возможно в результате того, что зарядная мощность линии оказывается равной потерям реактивной мощности Qc AQ. Qc Q), который направлен от середины линии в сторону обоих ее концов. Для компенсации этого превышения реактивная мощность направлена с обоих концов линии в ее середину. [13]

Источник

21.Зарядная мощность линии.

Емкость воздушной линии переменного тока практически не влияет на передаваемую мощность, однако через нее протекает так называемый зарядный ток, который создает зарядную мощность линии и приводит к дополнительному нагреву проводов, т.е. увеличивает потери энергии в линии и снижает ее КПД. Кроме того, этот ток приводит к нежелательному повышению напряжения в промежуточных точках линии и к целому ряду других отрицательных последствий. Поэтому возникает необходимость в компенсации зарядной мощности линии, для чего используются специальные устройства — реакторы, которые, в конечном счете, приводят к увеличению стоимости линии. Однако следует отметить, что необходимость в компенсации зарядной мощности линии, как правило, возникает лишь для линий сверхвысоких напряжений — 330 кВ и выше.

При работе воздушной линии на постоянном напряжении, когда по ней протекает постоянный ток, в установившемся режиме ни ее индуктивность, ни емкость не оказывают никакого влияния на процесс передачи электрической энергии по линии и, следовательно, на максимальную мощность, которую можно передать по линии при увеличении длины последней. Зарядная мощность линии постоянного тока отсутствует в силу изложенных выше причин. Поэтому сама линия не нуждается в каких-либо компенсирующих устройствах.

Главный вывод, который может быть сделан из сказанного выше, состоит в следующем:

для воздушной линии переменного тока существует зависимость максимальной передаваемой мощности от ее длины — чем длиннее линия, тем меньше предельная мощность, которую можно по ней передать; это одна из причин, ограничивающих допустимую длину такой линии;

воздушная линия постоянного тока не имеет такого ограничения, поэтому линия постоянного тока может иметь любую длину и передаваемую мощность, которые диктуются практической целесообразностью. Возможные ограничения — допустимые потери энергии на нагрев проводов и пропускная способность используемой аппаратуры.

Рассмотрим теперь кабельные линии. Известно, что кабельные линии переменного тока имеют весьма ограниченную длину — не более 15—20 км. Это объясняется двумя основными причинами:

большой зарядной мощностью, возникающей вследствие значительной емкости кабеля;

высокой стоимостью кабеля.

Зарядная мощность приводит к дополнительному нагреву жил кабеля, вынуждая снижать полезную передаваемую мощность и ограничивать длину кабеля. В особенности это относится к высоковольтным кабельным линиям (110—500 кВ). Поэтому кабельные линии переменного тока не могут быть использованы для передачи электроэнергии на достаточно большие расстояния.

В кабельной линии постоянного тока зарядная мощность отсутствует и не создает дополнительного нагрева кабеля. Поэтому кабельные линии постоянного тока могут сооружаться достаточно длинными (100—200 км, возможно и больше) и использоваться для решения задач, которые невозможно решить иными путями, например для пересечения больших водных пространств (морских проливов), ввода больших мощностей в центры крупных городов и др.

Источник

Расчёт режимов линий и определение в них потерь мощности

Страницы работы

Содержание работы

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №1

Тема: РАСЧЁТ РЕЖИМОВ ЛИНИЙ И ОПРЕДЕЛЕНИЕ В НИХ

1.1 Теоретические сведения

Расчёт установившегося режима заключается в определении токов и/или мощностей в отдельных элементах электрической сети, а также напряжений в её узлах.

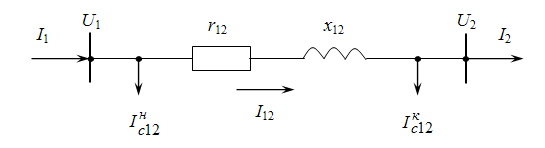
Схема замещения воздушной линии (ВЛ) номинальным напряжением 110-220 кВ и кабельной линии (КЛ) напряжением ≥35 кВ представлена на рисунке 1.

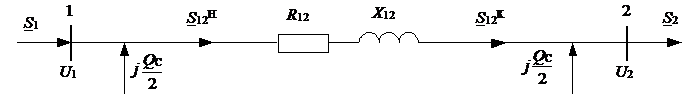Рисунок 1 – Схема замещения ВЛ 110-220 кВ и КЛ 35 кВ и выше

На рисунке 1 обозначены:

S₁ – мощность источника питания, входящая в линию (мощность узла 1);

S₂ – мощность потребителя, выходящая из линии (мощность узла 2, мощность нагрузки);

U₁ – напряжение источника питания (напряжение в узле 1, т.е. в начале линии);

U₂ – напряжение на шинах потребителя (напряжение в узле 1, т.е. в конце линии);

jQ_C – зарядная мощность линии (реактивная мощность, генерируемая самой линией);

R₁₂ – активное сопротивление линии;

X₁₂ – реактивное сопротивление линии;

S₁₂ Н – мощность в начале линии (мощность начала);

S₁₂ К – мощность в конце линии (мощность конца).

Перед расчётом режима линии необходимо рассчитать параметры её схемы замещения, к которым относятся активное сопротивление R₁₂, реактивное сопротивление X₁₂, а также зарядная мощность jQ_C, которая условно делится на две части – в начале и конце линии.

Активное и реактивное сопротивления линии определяются по паспортным данным (например, м/у 3260) в зависимости от марки и сечения проводов и длины линии:

где r₀ и x₀ – удельные (на единицу длины) активное и реактивное сопротивления проводов соответственно (м/у 3260, с.20-21, таблицы 2.4-2.5), [Ом/км] или [Ом/100] км;

Зарядная мощность линии находится по выражению:

[Мвар], (2)

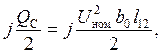
где U_ном – номинальное напряжение линии, [кВ];

b₀ – удельная емкостная проводимость линии, [См/км] (м/у 3260, с.20-21, таблицы 2.4-2.5).

Для расчёта режимов линий электропередачи характерны четыре основных случая:

1) Известны: напряжение в конце линии U₂ и мощность нагрузки S₂.

Найти: напряжение в начале линии U₁ и мощность источника питания S₁.

2) Известны: напряжение в начале линии U₁ и мощность источника питания S₁.

Найти: напряжение в конце линии U₂ и мощность нагрузки S₂.

3) Известны: напряжение в начале линии U₁ и мощность нагрузки S₂.

Найти: напряжение в конце линии U₂ и мощность источника питания S₁.

4) Известны: напряжение в конце линии U₂ и мощность источника питания S₁.

Найти: напряжение в начале линии U₁ и мощность нагрузки S₂.

Алгоритм расчёта режима линии для каждого из четырёх случаев.

– на основании 1-го закона Кирхгофа рассчитывается мощность S₁₂ К в конце линии:

, [МВА]; (3)

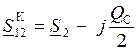
– определяются потери мощности в линии:

, [МВА], (4)

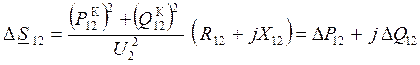
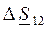
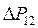
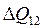
где , и – потери полной, активной и реактивной мощностей соответственно;

– находится мощность S₁₂ Н в начале линии:

; (5)

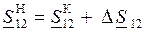
– на основании 1-го закона Кирхгофа рассчитывается мощность источника питания S₁:

; (6)

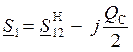
– по рассчитанной мощности в конце линии S₁₂ К и известному напряжению в конце линии U₂ определяется напряжение в начале линии U₁:

. (7)

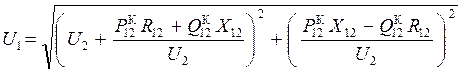
– на основании 1-го закона Кирхгофа рассчитывается мощность S₁₂ Н в начале линии:

, [МВА]; (8)

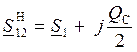
– определяются потери мощности в линии:

, [МВА], (9)

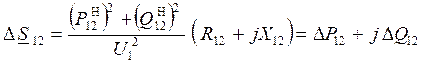
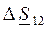
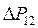
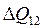
где , и – потери полной, активной и реактивной мощностей соответственно;

– находится мощность S₁₂ К в конце линии:

; (10)

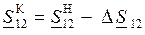
– на основании 1-го закона Кирхгофа рассчитывается мощность нагрузки S₂:

; (11)

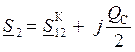
– по рассчитанной мощности в начале линии S₁₂ Н и известному напряжению в начале линии U₁ определяется напряжение в конце линии U₂:

. (12)

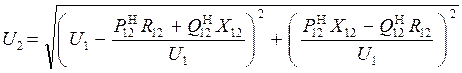
– по выражению (3) рассчитывается мощность S₁₂ К в конце линии;

– определяются потери мощности в линии по номинальному напряжению линии:

, [МВА], (13)

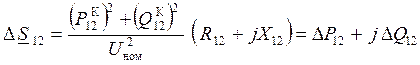
– находится мощность S₁₂ Н в начале линии по выражению (5);

– по выражению (6) рассчитывается мощность источника питания S₁;

– по формуле (12) определяется напряжение в конце линии U₂.

– по выражению (8) рассчитывается мощность S₁₂ Н в начале линии;

– определяются потери мощности в линии по номинальному напряжению линии:

, [МВА], (14)

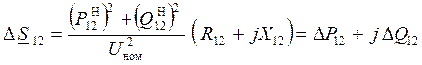
– по выражению (10) находится мощность S₁₂ К в конце линии;

– по выражению (11) рассчитывается мощность нагрузки S₂;

– по формуле (7) определяется напряжение в начале линии U₁.

1.2 Задание на самостоятельную работу

Для воздушной линии, показанной на рисунке 2, рассчитать режим. Исходные данные к расчёту приведены в таблице 1.

Источник

Вопрос 11 Вопрос 12 Зарядная мощность линии

Зарядная мощность линии не зависит от ее нагрузки. Реактивная индуктивная мощность, потребляемая линией, пропорциональна квадрату тока, протекающего по ней. При определенном значении нагрузки потребителей эти мощности станут равными, и так как зарядная мощность протекает навстречу реактивной индуктивной мощности, они взаимно скомпенсируются.

Из-за большой величины зарядной мощности линий сверхвысокого напряжения для дальних передач является обязательным применение поперечных реакторов, что является радикальным средством для снижения передачи реактивной мощности по линии и связанных с ней потерь энергии в режимах малых нагрузок. Мвар на передаваемый 1 МВт активной мощности.

Зарядная (емкостная) мощность трех фаз в конце линии:

–jQ к _с12=3I *к _с12U_2ф=

Необходимость учета емкости и зарядной мощности линии зависит от соиз-меряемости зарядной и нагрузочной мощности. В местных сетях небольшой протяженности при номинальных напряжениях до 35 кВ зарядные токи и мощности значительно меньше нагрузочных. Поэтому в КЛ емкостную проводимость учитывают только при напряжениях 20 и 35 кВ, а в ВЛ ею можно пренебречь

Вопрос 13 Расчет режима лэп при заданном токе нагрузки и напряжении в конце линии

Будем считать, что режим конца линии задан фазным напряжением U_ф=сonst и отстающим током нагрузки I₂. Также заданы Z₁₂=r₁₂+jx₁₂, в₁₂.

1) напряжение в начале линии – U₁,

2) ток в продольной части – I₁₂,

3) потери мощности – DS₁₂,

4) ток в начале линии – I₁.

Расчет состоит в определении неизвестных токов и напряжений, последовательно от конца линии к началу.

Емкостный ток в конце линии 1-2, по закону Ома:

Ток в продольной части линии 1-2, по первому закону Кирхгофа:

Напряжение в начале линии по закону Ома:

Емкостный ток в начале линии:

Ток в начале линии по первому закону Кирхгофа:

Потери мощности в линии (в трех фазах):

Векторная диаграмма токов и напряжений строится в соответствии с выражениями 1-5.

Вначале строим известные U_2ф и I₂.

Полагаем что U_2ф=U_2ф, т.е. напряжение U_2ф направлено по действительной оси. Емкостный ток I к _с12опережает на 90 о напряжение U_2ф. Ток I₁₂ соединяет начало первого и конец второго суммируеммых векторов в правой части урав.(2) [I₁₂=I₂+ I к _с12]

Вектор I₁₂∙r₁₂ параллелен вектору I₁₂, вектор I₁₂∙jx₁₂ опережает на 90 о ток I₁₂

Напряжение U_1ф соединяет начало и конец суммируемых векторов U_2ф, I₁₂∙r₁₂, I₁₂∙jx₁₂.

В линии с нагрузкой напряжение в конце линии по модулю меньше, чем в начале U_2ф к _с12 (2). I₁₂=I к _с12

В этом случае напряжение в конце линии повышается U_2ф>U_1ф

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник

Активная и реактивная проводимости линий. Эффект «короны». Зарядная мощность линии

Активная проводимость (g_л) линии соответствует двум видам потерь активной мощности:

1) от тока утечки через изоляторы;

2) потери на корону.

В связи с этим задаются наименьшие допустимые сечения по короне:

Коронирование проводов приводит:

-к усиленному окислению поверхности проводов,

-к появлению радиопомех.

При расчете установившихся режимов сетей до 220 кВ активная проводимость практически не учитывается.

В сетях с при определении потерь мощности при расчете оптимальных режимов, необходимо учитывать потери на корону.

,

(2),

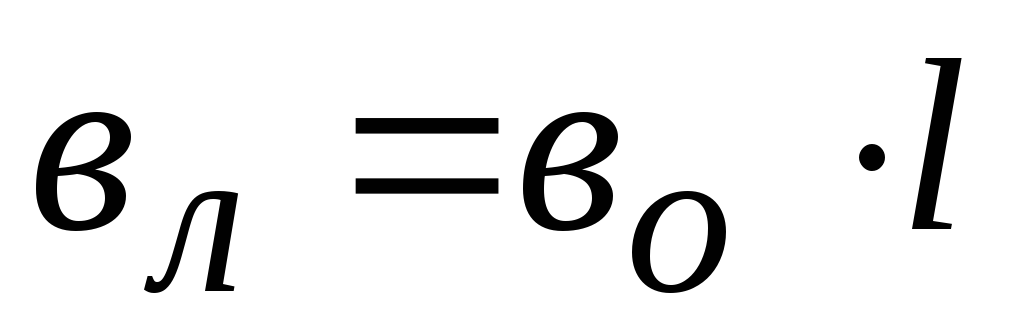
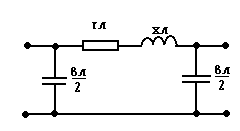
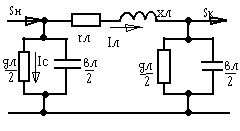
Для большинства расчетов в сетях 110-220 кВ ЛЭП (линия электропередачи) представляется более простой схемой замещения:

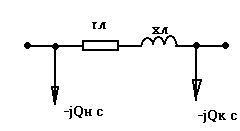
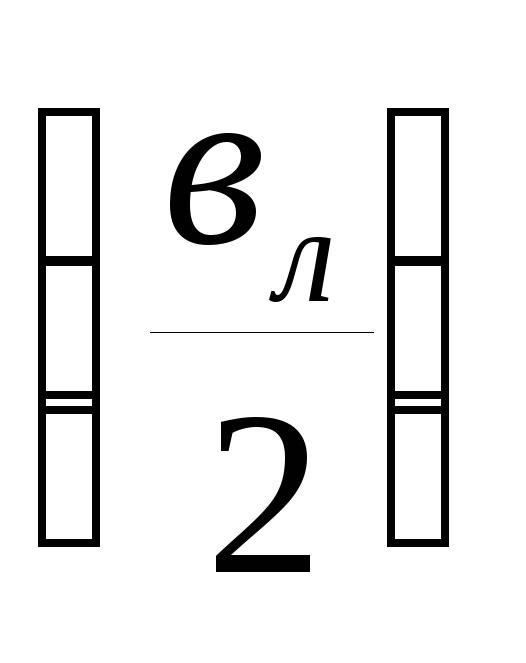
Иногда в схеме замещения вместо емкостной проводимостиучитывается реактивная мощность, генерируемая емкостью линий (зарядная мощность).

Половина емкостной мощности линии, МВАр, равна:

(*),

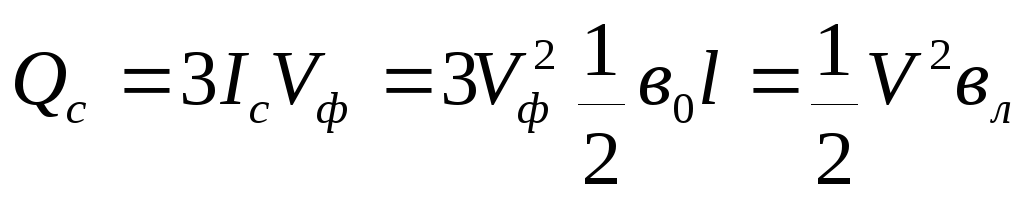
U_ф и U – соответственно фазное и междуфазное (линейное) напряжения, кВ;

Из выражения для Q_с (*) следует, что мощность Q_с, генерируемая линий сильно зависит от напряжения. Чем выше напряжение, тем больше емкостная мощность.

Для воздушных линий напряжением 35 кВ и ниже емкостную мощность (Q_с) можно не учитывать, тогда схема замещения примет следующий вид:

Для линий с 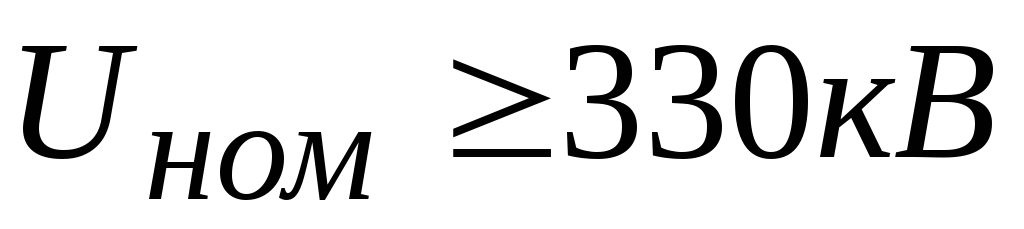при длине > 300-400 км учитывают равномерное распределение сопротивлений и проводимостей вдоль линии.

Схемы замещений кл для напряжений 10-220 кВ

Кабельные линии электропередачи представляют такой же П-образной схемой замещения как и ВЛ.

Удельные активные и реактивные сопротивления r₀, х₀ определяют по справочным таблицам, так же как и для ВЛ.

видно, что х₀ уменьшается, а в₀ растет при сближении разных проводов.

Для кабельных линий расстояние между проводами фаз значительно меньше, чем для ВЛ и Х₀ очень мало.

При расчетах режимов КЛ (кабельных линий) напряжением 10кВ и ниже можно учитывать только активное сопротивление.

Емкостный ток и Q_с в кабельных линиях больше чем в ВЛ. В кабельных линиях (КЛ) высокого напряжения учитывают Q_с, причем удельную емкостную мощность Q_c0 кВАр/км можно определить по таблицам в справочниках.

Активную проводимость (g_л )учитывают для кабелей 110 кВ и выше.

Удельные параметры кабелей х₀, а также Q_с0 приведенные в справочных таблицах ориентировочны, более точно их можно определить по заводским характеристикам кабелей.

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник