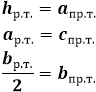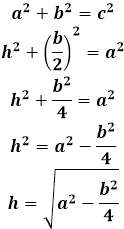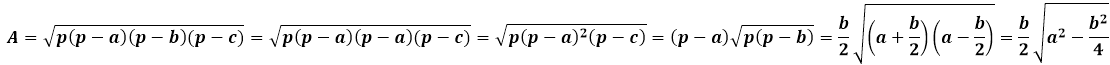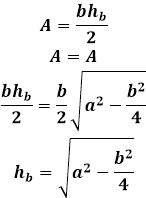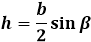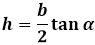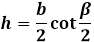что такое высота равнобедренного треугольника
Равнобедренный треугольник: свойства, признаки и формулы
Содержание:
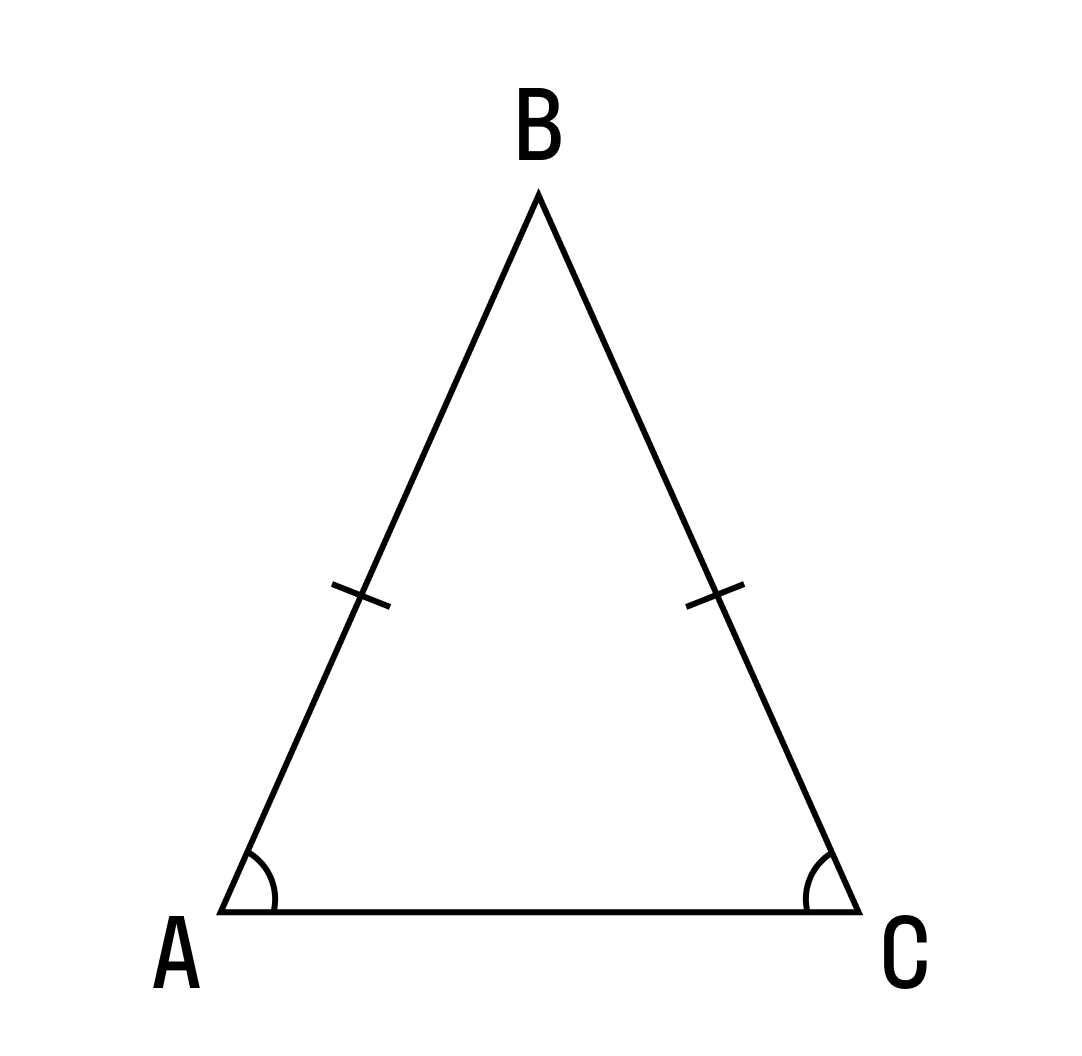
Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, а третья сторона — основанием.
АВ = ВС — боковые стороны
Свойства равнобедренного треугольника
Свойства равнобедренного треугольника выражаются через 5 теорем:
Теорема 1. В равнобедренном треугольнике углы при основании равны.
Доказательство теоремы:
Рассмотрим равнобедренный Δ ABC с основанием АС.
Боковые стороны равны АВ = ВС,
Следовательно углы при основании ∠ BАC = ∠ BСA.
Теорема о биссектрисе, медиане, высоте, проведенной к основанию равнобедренного треугольника
Доказательство теоремы:
Вывод:
Запомни! При решении таких задач опусти высоту на основание равнобедренного треугольника. Чтобы разделить его на два равных прямоугольных треугольника.
Доказательство теоремы:
Доказательство от противного.
Признаки равнобедренного треугольника
Формулы равнобедренного треугольника
Формулы сторон равнобедренного треугольника
Формулы длины стороны (основания — b):
Формулы длины равных сторон — (а):
Формулы высоты, медианы, биссектрисы равнобедренного треугольника
Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):
Формула высоты, биссектрисы и медианы, через стороны, (L):
Площадь равнобедренного треугольника
Формула площади треугольника через высоту h и основание b, (S):
Высота равнобедренного треугольника

Всего получено оценок: 80.
Всего получено оценок: 80.
Из-за двух равных сторон, равнобедренный треугольник обладает рядом специфических свойств, за которые его очень любят составители задач. Рассмотрим, чем же выделяется высота равнобедренного треугольника и как ее лучше найти.
Определение
В общем случае, высота – это перпендикуляр, опущенный из вершины фигуры на противолежащую сторону. В равнобедренном треугольнике под высотой обычно подразумевают высоту, опущенную на основание.
Если по условию задачи нужно найти значение высоты равнобедренного треугольника без уточнений, какую именно требуется найти, то имеется в виду высота, опущенная на основание.
Необходимые теоремы
Для решения задач на определение высоты равнобедренного треугольника, нужно знать теорему Пифагора и свойство высоты равнобедренного треугольника.
Теорема Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Свойство: в равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой.
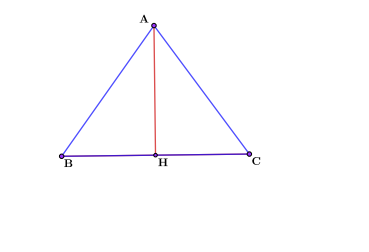
Из теоремы и свойства следует основная формула высоты равнобедренного треугольника. Рассмотрим равнобедренный треугольник АВС с высотой АН и основанием ВС. Тогда треугольник АВН является прямоугольным. Запишем значение высоты через теорему Пифагора, так как в треугольнике АВН высота АН является катетом.
$$ВН=<1\over2>*ВС$$, так как по свойству высоты равнобедренного треугольника АН является медианой. Это и есть формула высоты равнобедренного треугольника.
Задача
Решим задачу, где будет задействована не только высота, проведенная к основанию, но и другая высота. В равнобедренном треугольнике, как и в любом другом, их три. В задаче также будет применен способ нахождения высоты, который можно использовать для любого треугольника, а не только для равнобедренного.
В Равнобедренном треугольнике АВС с основанием ВС проведены высоты АН и ВР. Синус угла АСВ равен 0,6, а боковая сторона 5. Найти высоту ВР.
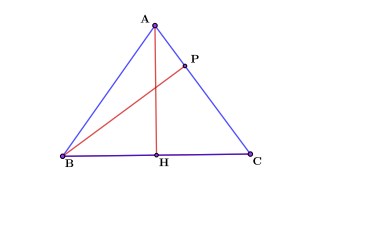
Для начала, необходимо найти значение высоты, проведенной к основанию и основание. Для этого обратим внимание на прямоугольный треугольник АСН. Воспользуемся определением синуса.
Синус угла это отношение противолежащего катета к гипотенузе. Нам известно значение синуса, значит:
$$<АН\over<АС>>=0,6$$ – из этого отношения выразим значение АН.
Через теорему Пифагора найдем значение НС:
Тогда основание равно:
Теперь найдем площадь треугольника:
С другой стороны площадь можно найти и через высоту ВР.
$$S=<1\over2>*ВР*АС$$ – так как ВР это высота, проведенная к стороне АС.
Значит верно равенство:
Что мы узнали?
Мы вывели формулу высоты прямоугольного треугольника. Определили, что высота в прямоугольном треугольнике может находиться любым способом, связанным с произвольным треугольником и решили интересную задачу на нахождение высоты треугольника.
Высота равнобедренного треугольника
Равнобедренным треугольником называется такой треугольник, у которого две из трех сторон равны между собой. Равные стороны считаются боковыми сторонами а, а третья сторона в называется основанием равнобедренного треугольника.
Рассмотрим каждый случай по отдельности.
Высота равнобедренного треугольника, опущенная на основание, обладает рядом индивидуальных свойств, присущих только ей и не распространяющихся на другие высоты в таком треугольнике. В частности, высота, проведенная к основанию равнобедренного треугольника, совпадает с медианой и биссектрисой, проведенным к основанию, следовательно, она не только образует прямой угол с основанием, но и делит его на две равные части, как медиана, и аналогично делит угол пополам, как биссектриса. В итоге, высота является своеобразной осью симметрии треугольника и разделяет его на два конгруэнтных прямоугольных треугольника. В таком треугольнике высота является катетом, и чтобы найти ее длину необходимо соотнести стороны равнобедренного треугольника со сторонами прямоугольного. Боковая сторона равнобедренного треугольника становится гипотенузой, а чтобы определить второй катет, основание равнобедренного треугольника нужно разделить пополам, по свойству медианы.
Длина высоты равнобедренного треугольника равна по теореме Пифагора квадратному корню из суммы квадрата боковой стороны равнобедренного треугольника и четверти квадрата основания равнобедренного треугольника:
Второй случай, когда условиями задачи нужно найти высоту, опущенную на боковую сторону равнобедренного треугольника, раскрывается проще всего через площадь треугольника.
Формула Герона для равнобедренного треугольника будет иметь несколько упрощенный вид за счет того, что значения боковых сторон повторяются:
Площадь равнобедренного треугольника через высоту, опущенную к боковой стороне
Эту же формулу можно применять для нахождения любой высоты в равнобедренном треугольнике, если поменять в формуле соответствующие стороны местами.
Формула высоты равнобедренного треугольника через боковую сторону и угол при основании α: h=a sinα
Формула через боковую сторону и угол напротив основания β:
Формула через основание и угол при нем α:
через основание и угол противолежащий ему β:
Равнобедренные треугольники
1. В равнобедренном треугольнике углы при основании равны.
2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
3. Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.
4. Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.
5. Углы, противолежащие равным сторонам равнобедренного треугольника, всегда острые.
6. В равнобедренном треугольнике:
— биссектрисы, проведенные из вершин при основании, равны;
— высоты, проведенные из вершин при основании, равны;
— медианы, проведенные из вершин при основании, равны.
7. Центры вписанной и описанной окружностей лежат на высоте, биссектрисе и медиане, проведенных к основанию.
8. Вписанная окружность точкой касания делит основание пополам.
Внешним углом треугольника называется угол, смежный с каким-либо углом этого треугольника.
Внешний угол треугольника равен сумме двух углов, не смежных с ним.
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
Соотношение между сторонами и углами в прямоугольном треугольнике:
Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Во всяком треугольнике стороны относятся как синусы противолежащих углов:
Воспользуемся теоремой синусов:
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной окружности
Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
Равнобедренный треугольник: свойства, признаки и формулы
Определение равнобедренного треугольника
Какой треугольник называется равнобедренным?
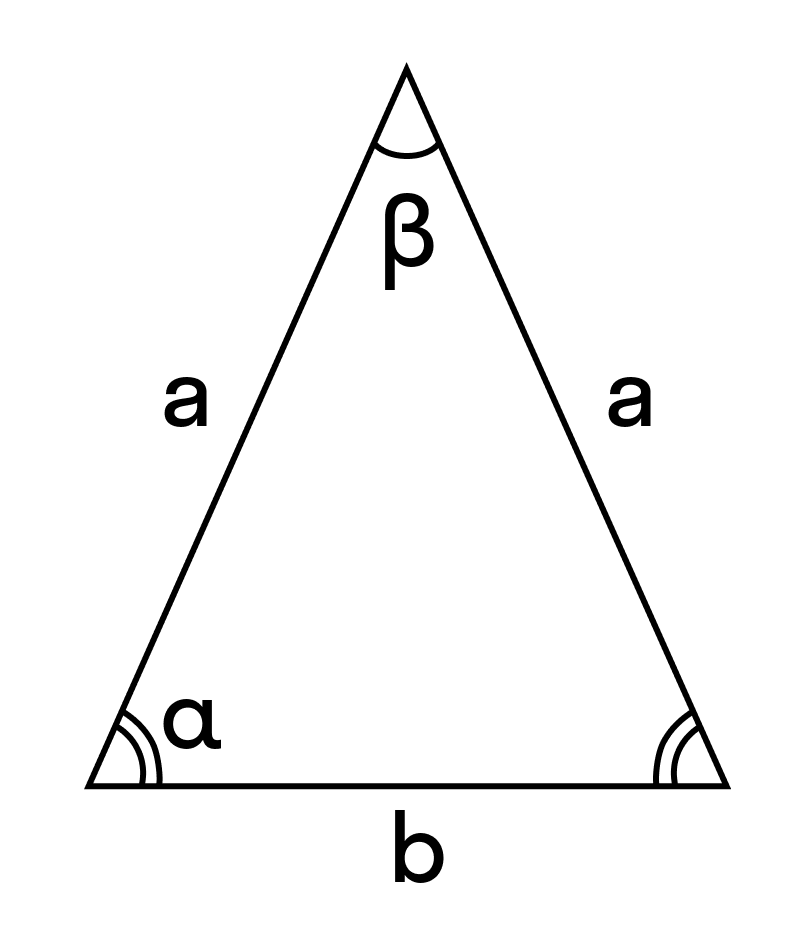
Давайте посмотрим на такой треугольник:
На рисунке хорошо видно, что боковые стороны равны. Это равенство и делает треугольник равнобедренным.
А вот как называются стороны равнобедренного треугольника:
AB и BC — боковые стороны,
AC — основание треугольника.
Чтобы найти основание равнобедренного треугольника, используйте формулу: b = 2a cos
Свойства равнобедренного треугольника
Чтобы понять суть равнобедренного треугольника, нужно думать как равнобедренный треугольник, стать равнобедренным треугольником — и выучить 5 теорем.
Теоремы помогут доказать, что треугольник равнобедренный, а не какой-нибудь ещё. Давайте приступим.
Теорема 1. В равнобедренном треугольнике углы при основании равны.
Мы выяснили, что AС — основание равнобедренного треугольника. Поскольку боковые стороны треугольника равны AB = СB, то и углы при основании — равны. ∠ BАC = ∠ BСA. Изи!
Теорема 2: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
Теорема 3: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Теорема 4: В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
Чтобы доказать все эти теоремы, вспомним, что такое биссектриса, медиана и высота.
Биссектриса — луч, который исходит из вершины угла и делит этот угол на два равных угла.
Даже если вы не знаете определения, то про крысу, бегающую по углам и делящую их пополам, наверняка слышали. Она не даст вам забыть, что такое биссектриса. А если вам не очень приятны крысы, то вместо нее бегать может кто угодно. Биссектриса — это киса. Биссектриса — это лИса. Никаких правил для воображения нет. Все правила — для геометрии.
Обратите внимание на рисунок. В представленном равнобедренном треугольнике биссектрисой будет отрезок BH.
Медиана — линия, которая соединяет вершину треугольника с серединой противолежащей стороны.
Для медианы не придумали веселого правила, как с биссектрисой, но можно его придумать. Например, буддийская запоминалка: «Медиана — это Лама, бредущий из вершины треугольника к середине его основания и обратно».
В данном треугольнике медианой является отрезок BH.
Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону.
Высотой в представленном равнобедренном треугольнике является отрезок BH.
Доказательство теорем 2, 3, 4 будет коллективным, поскольку из определений видно, что биссектриса, медиана и высота равнобедренного треугольника — это одно и то же.
А вот и доказательство:
Вуаля, сразу три теоремы доказаны.
Теорема 5: Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны (третий признак равенства треугольников).
Дано два Δ ABC = Δ A1B1C1.
Чтобы доказать равенство треугольников, мысленно наложите один треугольник на другой так, чтобы стороны совпали. Точка A должна совпасть с точкой А1, точка B должна совпасть с точкой B2, точка С — с точкой С1.
Если все стороны совпадают — треугольники равны, а теорема доказана.
Признаки равнобедренного треугольника
Вот несколько нехитрых правил, по которым легко определить, что перед вами не что иное, как его величество равнобедренный треугольник.
Формулы равнобедренного треугольника
Формулы сторон равнобедренного треугольника
b — основание равнобедренного треугольника
a — равные стороны равнобедренного треугольника
α — углы при основании
β — угол, образованный равными сторонами
Формулы длины стороны (основания b) равнобедренного треугольника
Формулы длины равных сторон равнобедренного треугольника (стороны a):
Формулы высоты, медианы, биссектрисы равнобедренного треугольника
b — основание равнобедренного треугольника
a — равные стороны равнобедренного треугольника
α — углы при основании
β — угол, образованный равными сторонами
L — высота, биссектриса и медиана
Формулы высоты, биссектрисы и медианы равнобедренного треугольника, через сторону и угол (L)
Формула высоты, биссектрисы и медианы равнобедренного треугольника, через стороны (L)
Примеры решения задач
Нет ничего приятнее, чем поупражняться и поискать градусы и длины в равнобедренном треугольнике. Ну… почти ничего.
Задачка раз. Дан ABC: ∠C = 80∘, AB = BC. Найдите ∠B.
Поскольку вы уже знакомы с пятью теоремами, то для вас не секрет, что углы при основании в равнобедренном треугольнике равны.
∠A = ∠C = 80∘.
Не должно вас удивить и то, что сумма углов треугольника равна 180∘
∠B = 180∘ − 80∘ − 80∘ = 20∘.
∠B = 20∘
Задачка два. В равнобедренном треугольнике один из углов равен 110∘. Найдите наибольший из внешних углов этого треугольника.
Вспоминаем первую теорему о равенстве углов при основании (а лучше не забываем вовсе). Поскольку сумма углов = 180∘, то второго угла в 110∘ в нём быть не может. Соответственно, известный угол в 110∘ — это угол при вершине. (180∘−110∘)/2=35∘. Внешние углы треугольника равны: 180∘−110∘=70∘,180∘−35∘=145∘,180∘−35∘=145∘. Больший внешний угол равен 145∘