что такое геометрическая фигура
Геометрические фигуры. Основные геометрические фигуры.
Основными геометрическими фигурами на плоскости являются точка и прямая линия. Отрезок, луч, ломаная линия — самые простые геометрические фигуры на плоскости.
Точка — мельчайшая геометрическая фигура, являющаяся основой других фигур во всяком изображении либо чертеже.
Каждая более сложная геометрическая фигура есть множество точек, которые обладают определенным свойством, характерное только для этой фигуры.
Прямая линия, либо прямая – это бесконечное множество точек, расположенных на 1-ой линии, которая не имеет начала и конца. На листе бумаги можно увидеть лишь часть прямой линии, т.к. она не имеет предела.
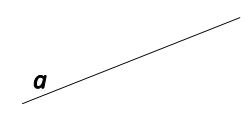
Прямую изображают так:
Часть прямой линии, которая ограничена с 2-х сторон точками, называют отрезком прямой, либо отрезком. Его изображают так:
Луч — это направленная полупрямая, имеющая точку начала и у которой нет конца. Луч изображают так:
Если на прямой поставить точку, то эта точка будет разбивать прямую на 2 противоположно направленных луча. Эти лучи называют дополнительными.
Ломаная линия — несколько отрезков, которые соединены друг с другом таким образом, что конец 1-го отрезка оказывается началом 2-го отрезка, а конец 2-го отрезка — началом 3-го отрезка и так далее, причем соседние (которые имеют 1-ну общую точку) отрезки располагаются на разных прямых. Когда конец последнего отрезка не совпадает с началом 1-го, значит, эта ломаная линия будет называться незамкнутой:
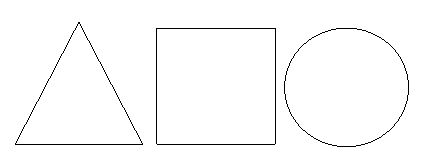
Четырехзвенная замкнутая ломаная линия — четырехугольник (прямоугольник):
Трехзвенная замкнутая ломаная линия — треугольник:
Плоскость, как и прямая, — это исходное понятие, у которого нет определения. У плоскости, как и у прямой, не возможно увидеть ни начала, ни конца. Всегда рассматривается лишь часть плоскости, ограниченная замкнутой ломаной линией.
Что такое геометрическая фигура
Геометрические фигуры – это совокупность множества точек, линий, поверхностей или тел, которые расположены на поверхности, плоскости или пространстве и формирует конечное количество линий.
Термин «фигура» в какой-то степени формально применяется к множеству точек, но как правило фигурой принято называть такие множества, которые расположенные на плоскости и ограничиваются конечным числом линий.
Что такое геометрия
Геометрия – это такая математическая наука, которая занимается изучением свойств геометрических фигур. Если дословно перевести на русский язык термин «геометрия», то он обозначает «землемерие», так как в стародавние времена основной задачей геометрии, как науки, стало измерение расстояний и площадей на поверхности земли.
Практическое применение геометрии бесценно во все времена и независимо от профессии. Без знаний геометрии не может обойтись ни рабочий, ни инженер, ни архитектор и даже художник.
В геометрии есть такой раздел, который занимается изучением различных фигур на плоскости и называется планиметрия.
Вам уже известно, что фигурой называют произвольное множество точек, находящиеся на плоскости.
К геометрическим фигурам принадлежат: точка, прямая, отрезок, луч, треугольник, квадрат, круг и другие фигуры, которые изучает планиметрия.
Точка
Из выше изученного материала вам уже известно, что точка относится к главным геометрическим фигурам. И хотя это самая малая геометрическая фигура, но она необходима для построения других фигур на плоскости, чертеже или изображении и является основой для всех остальных построений. Ведь построение более сложноватых геометрических фигур складывается из множества точек, характерных для данной фигуры.
В геометрии точки обозначают прописными буквами латинского алфавита, например, такими, как: А, В, С, D ….
А теперь подведем итог, и так, с математической точки зрения, точка является таким абстрактным объектом в пространстве, который не имеет объема, площади, длины и других характеристик, но остается одним из фундаментальных понятий в математике. Точка – это такой нульмерный объект, которые не имеет определения. По определению Евклида, точкой называют то, что невозможно определить.
Прямая
Как и точка, прямая относится к фигурам на плоскости, которая не имеет определения, так как состоит из бесконечного множества точек, находящихся на одной линии, которая не имеет ни начала ни конца. Можно утверждать, что прямая линия бесконечна и не имеет предела.
Если же прямая начинается и заканчивается точкой, то она уже не является прямой и называется отрезком.
Но иногда прямая, с одной стороны имеет точку, а с другой нет. В таком случае прямая превращается в луч.
Если же взять прямую и на ее средине поставить точку, то она разобьет прямую на два противоположно направленных луча. Данные лучи являются дополнительными.
Если же перед вами несколько отрезков, соединенных между собой так, что конец первого отрезка становиться началом второго, а конец второго отрезка — началом третьего и т. д., и эти отрезки находятся не на одной прямой и при соединении имеют общую точку, то такая цепочка является ломаной линией.
• Какая ломаная линия называется незамкнутой?
• Как обозначается прямая?
• Как называется ломаная линия, у которой четыре замкнутых звена?
• Какое название имеет ломаная линия с тремя замкнутыми звеньями?
Когда конец последнего отрезка ломаной совпадает с началом 1-го отрезка, то такую ломаную линию называют замкнутой. Примером замкнутой ломаной является любой многоугольник.
Плоскость
Как точка и прямая, так и плоскость является первичным понятием, не имеет определения и у нее нельзя увидеть ни начала, ни конца. Поэтому, при рассмотрении плоскости, мы рассматриваем только ту ее часть, которая ограничивается замкнутой ломаной линией. Таким образом, плоскостью можно считать любую гладкую поверхность. Этой поверхностью может быть лист бумаги или стола.
Фигура, которая имеет два луча и вершину, называется углом. Место соединения лучей, является вершиной этого угла, а его сторонами считаются лучи, которые этот угол образуют.
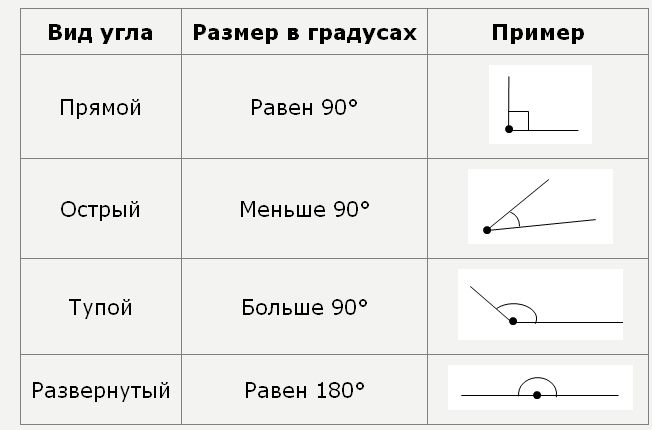
1. Как в тексте обозначают угол?
2. Какими единицами можно измерить угол?
3. Какие бывают углы?
Параллелограмм
Прямоугольник, квадрат и ромб являются частными случаями параллелограмма.
Параллелограмм, имеющий прямые углы равные 90 градусам, является прямоугольником.
Квадрат — это тот же параллелограмм, у него и углы и стороны равны.
Что до определения ромба, то это такая геометрическая фигура, все стороны которого равны.
Кроме того, следует знать, что любой квадрат является ромбом, но не каждый ромб может быть квадратом.
Трапеция
При рассмотрении такой геометрической фигуры, как трапеция, можно сказать, что в частности она, как и четырехугольник имеет одну пару параллельных противолежащих сторон и является криволинейной.
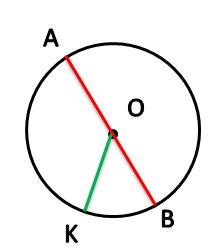
Окружность и круг
Окружность — геометрическое место точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное ненулевое расстояние, называемое её радиусом.
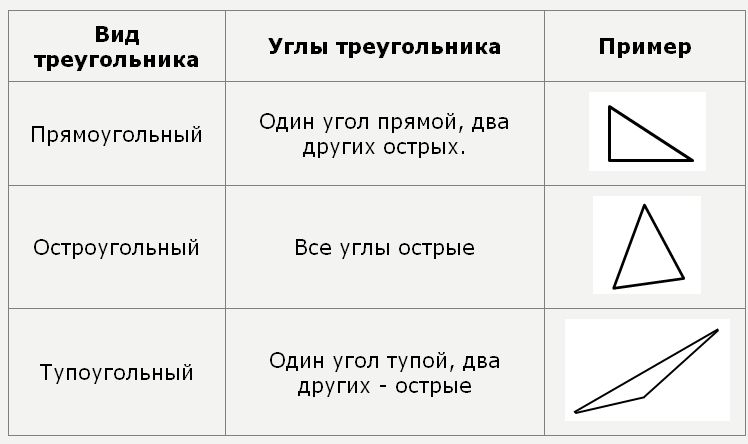
Треугольник
Также к простым геометрическим фигурам принадлежит и уже изучаемый вами треугольник. Это один из видов многоугольников, у которого часть плоскости ограничена тремя точками и тремя отрезками, которые соединяют эти точки попарно. Любой треугольник имеет три вершины и три стороны.
Задание: Какой треугольник называют вырожденным?
Многоугольник
К многоугольникам относятся геометрические фигуры разных форм, у которых замкнутая ломаная линия.
В многоугольнике все точки, которые соединяют отрезки, являются его вершинами. А отрезки, из которых состоит многоугольник, являются его сторонами.
Интересные факты
• А известно ли вам, что возникновение геометрии уходит в глубину веков и связано с развитием различных ремесел, культуры, искусства и наблюдением за окружающим миром. Да и название геометрических фигур является тому подтверждением, так как их термины, возникли не просто так, а благодаря своей схожести и подобию.
• Ведь термин «трапеция» в переводе с древнегреческого языка от слова «трапезион» обозначает столик, трапеза и другие производные слова.
• «Конус» произошел от греческого слова «конос», что в переводе звучит, как сосновая шишка.
• «Линия» имеет латинские корни и происходит от слова «линум», в переводе это звучит, как льняная нить.
• А знаете ли вы, что если взять геометрические фигуры с одинаковым периметром, то среди них обладателем самой большой площади оказался круг.
• А вот одна из известных картин, созданная еще в начале прошлого века Малевичем, прославляет такую геометрическую фигуру, как квадрат. Черный квадрат на белом фоне является мистической загадкой для окружающих, притягивая к себе исследователей и восхищенные взгляды живописцев.
Геометрические фигуры. Особенности восприятия детьми формы предметов и геометрических фигур
Чукур Людмила Васильевна
Геометрические фигуры. Особенности восприятия детьми формы предметов и геометрических фигур
«ГЕОМЕТРИЧЕСКАЯ ФИГУРА.
ОСОБЕННОСТИ ВОСПРИЯТИЯ ДЕТЬМИ
ФОРМЫ ПРЕДМЕТОВ И ГЕОМЕТРИЧЕСКИХ ФИГУР»
Подготовила: ст. воспитатель Чукур Л. В.
1. Понятие «геометрическая фигура». Особенности развития представлений о форме предметов у детей дошкольного возраста
Одним из свойств окружающих предметов является их форма. Форма предметов получила обобщенное отражение в геометрических фигурах.
Наблюдая за предметами окружающего мира, люди заметили, что есть некоторое общее свойство, позволяющее объединить предметы в одну группу. Это свойство было названо геометрической фигурой. Геометрическая фигура – это эталон для определения формы предмета, всякое непустое множество точек; обобщенное абстрактное понятие.
Само определение понятия геометрической фигуры дали древние греки. Они определили, что геометрической фигурой является внутренняя область, ограниченная замкнутой линией на плоскости. Активно это понятие применял в своей работе Евклид. Древние греки классифицировали все геометрические фигуры и дали им названия.
Упоминание о первых геометрических фигурах встречается и у древних египтян и древних шумеров. Учеными-археологами был найден папирусный свиток с геометрическими задачами, в которых упоминались геометрические фигуры. И каждая из них называлась каким-то определенным словом.
Таким образом, представление о геометрии и изучаемых этой наукой фигурах имели люди с давних времен, но название, «геометрическая фигура» и названия всем геометрическим фигурам дали древнегреческие ученые.
В наше время знакомство с геометрическими фигурами начинается с раннего детства и продолжается на всём пути обучения. Дошкольники, познавая окружающий мир, сталкиваются с разнообразием форм предметов, учатся называть и различать их, а затем знакомятся и со свойствами геометрических фигур.
Форма – это внешнее очертание предмета. Множество форм бесконечно.
Представления о форме предметов возникают у детей достаточно рано. В исследованиях Л. А. Венгера выясняется, возможно ли различение формы предметов детьми, у которых еще не сформировался акт хватания. В качестве индикатора он использовал ориентировочную реакцию ребенка в возрасте 3-4 месяцев.
Л. А. Венгер заметил также, что что на геометрической фигуре с изменением пространственной ориентации возникает такое же зрительное сосредоточение, как и на новой геометрической фигуре.
Исследования М. Денисовой и Н. Фигурина показали, что грудной ребенок по форме на ощупь определяет бутылочку, соску, материнскую грудь. Зрительно дети начинают различать форму предметов с 5 месяцев. При этом индикатором различения являются движения рук, корпуса по направлению к экспериментальному объекту и схватывание его (при пищевом подкреплении).
В других исследованиях выявлено, что, если предметы отличаются цветом, то ребенок 3-х лет выделяет их форму только в том случае, если предмет знаком ребенку из практического опыта (опыт манипуляций, действий).
Это доказывает и тот факт, что ребенок одинаково узнает прямые и перевернутые изображения (может рассматривать и понимать знакомые картинки, держа книжку «вверх ногами», предметы, окрашенные в несвойственные цвета (черное яблоко, но квадрат, повернутый на угол, т. е. в виде ромба, не узнает, так как исчезает непосредственное сходство формы предмета, которого нет в опыте.
2. Особенности восприятия детьми дошкольного возраста формы предметов и геометрических фигур
Одним из ведущих познавательных процессов детей дошкольного возраста является восприятие. Восприятие помогает отличить один предмет от другого, выделить какие-то предметы или явления из других похожих на него.
Первичное овладение формой предмета осуществляется в действиях с ним. Форма предмета, как таковая, не воспринимается отдельно от предмета, она является его неотъемлемым признаком. Специфические зрительные реакции прослеживания контура предмета появляются в конце второго года жизни и начинают предшествовать практическим действиям. Действия детей с предметами на разных этапах различны.
Исследования психолога С. Н. Шабалина показывают, что геометрическая фигура воспринимается дошкольниками своеобразно. Если взрослый воспринимает ведро или стакан как предметы, имеющие цилиндрическую форму, то в его восприятие включается знание геометрических форм. У дошкольника происходит обратное явление.
В 4-5 лет ребенок начинает сравнивать геометрическую фигуру с предметом: про квадрат говорит «это как платочек».
В результате организованного обучения дети начинают выделять в окружающих предметах знакомую геометрическую фигуру, сравнивать предмет с фигурой (стаканчик как цилиндр, крыша как треугольник, учится давать правильное название геометрической фигуры и формы предмета, в их речи появляются слова «квадрат», «круг», «квадратный», «круглый» и т. п.
Проблему знакомства детей с геометрическими фигурамии их свойствами следует рассматривать в двух аспектах:
• в плане сенсорного восприятия форм геометрических фигур и использования их как эталонов в познании форм окружающих предметов;
• в смысле познания особенностей их структуры, свойств, основных свя-зей и закономерностей в их построении, т. е. собственно геометри-ческого материала.
Контур предмета это общее начало, которое является исходным как для зрительного, так и для осязательного восприятия. Однако вопрос о роли контура в восприятии формы и формировании целостного образа требует еще дальнейшей разработки.
Первичное овладение формой предмета осуществляется в действиях с ним. Форма предмета, как таковая, не воспринимается отдельно от предмета, она является его неотъемлемым признаком. Специфические зрительные реакции прослеживания контура предмета появляются в конце второго года жизни и начинают предшествовать практическим действиям.
Уже на втором году жизни дети свободно выбирают фигурупо образцу из таких пар: квадрат и полукруг, прямоугольник и треугольник. Но различать прямоугольник и квадрат, квадрат и треугольник дети могут лишь после 2,5 лет. Отбор же по образцу фигур более сложной формы доступен примерно на рубеже 4-5 лет, а воспроизведение сложной фигуры осуществляют дети пятого и шестого года жизни.
Под обучающим воздействием взрослых восприятие геометрических фигур постепенно перестраивается. Геометрические фигуры начинают восприниматься детьми как эталоны, с помощью которых познание структуры предмета, его формы и размера осуществляется не только в процессе восприятия той или иной формы зрением, но и путем активного осязания, ощупывания ее под контролем зрения и обозначения словом.
Совместная работа всех анализаторов способствует более точному восприятию формы предметов. Чтобы лучше познать предмет, дети стремятся коснуться его рукой, взять в руки, повернуть; причем рассматривание и ощупывание различны в зависимости от формы и конструкции познаваемого объекта. Поэтому основную роль в восприятии предмета и определении его формы имеет обследование, осуществляемое одновременно зрительным и двигательно-осязательным анализаторами с последующим обозначением словом. Однако у дошкольников наблюдается весьма низкий уровень обследования формы предметов; чаще всего они ограничиваются беглым зрительным восприятием и поэтому не различают близкие по сходству фигуры (овал и круг, прямоугольник и квадрат, разные треугольники).
Сравнение фигуры с формой того или иного предмета помогает детям понять, что с геометрическими фигурами можно сравнивать разные предметы или их части. Так, постепенно геометрическая фигура становится эталоном определения формы предметов.
3. Особенности обследования и этапы обучения обследованию детьми дошкольного возраста формы предметов и геометрических фигур
Известно, что в основе познания всегда лежит сенсорное обследование, опосредованное мышлением и речью. В исследованиях Л. Венгера с детьми 2-3 лет индикатором зрительного различения формы предметов служили предметные действия ребенка.
По исследованиям С. Якобсон, В. Зинченко, А. Рузской дети 2-4 лет лучше узнавали предметы по форме, когда предлагалось сначала ощупать предмет, а потом найти такой же. Более низкие результаты наблюдались тогда, когда предмет воспринимался зрительно.
Исследования Т. Гиневской раскрывают особенности движений рук при обследовании предметов по форме. Детям завязывали глаза и предлагали ознакомиться с предметом путем осязания.
В 3-4 года – движения исполнительные (катают, стучат, возят). Движения немногочисленны, внутри фигуры, иногда (однократно) по осевой линии, много ошибочных ответов, смешение разных фигур. В 4-5 лет – движения установочные (зажимают в руке). Количество движений увеличивается в два раза; судя по траектории, ориентированы на размер и площадь; крупные, размашистые, обнаруживаются группы близко расположенных фиксаций, относящихся к наиболее характерным признакам фигуры; дают более высокие результаты. В 5-6лет – движения обследовательские (прослеживание контура, проверка на упругость). Появляются движения, прослеживающие контур, однако они охватывают наиболее характерную часть контура, другие части оказываются необследованными; движения внутри контура, количество то же, высокие результаты; как и в предыдущий период, наблюдается смешение близких фигур. В 6-7 лет – движения по контуру, пересечение поля фигуры, причем движения сосредотачиваются на наиболее информативных признаках, наблюдаются отличные результаты не только при узнавании, но и при воспроизведении.
Таким образом, для того, чтобы ребенок выделил существенные признаки геометрических фигур, необходимо их зрительное и двигательное обследование. Движения рук организовывают движения глаз и этому детей необходимо научить.
Этапы обучения обследованию
Второй этап обучения детей 5-6 лет должен быть посвящен формированию системных знаний о геометрических фигурах и развитию у них начальных приемов и способов «геометрического мышления».
«Геометрическое мышление» вполне возможно развить еще в дошкольном возрасте. В развитии «геометрических знаний» у детей прослеживается несколько различных уровней.
Первый уровень характеризуется тем, что фигура воспринимается детьми как целое, ребенок еще не умеет выделять в ней отдельные элементы, не замечает сходства и различия между фигурами, каждую из них воспринимает обособленно.
На втором уровне ребенок уже выделяет элементы в фигуре и устанавливает отношения как между ними, так и между отдельными фигурами, однако еще не осознает общности между фигурами.
На третьем уровне ребенок в состоянии устанавливать связи между свойствами и структурой фигур, связи между самими свойствами. Переход от одного уровня к другому не является самопроизвольным, идущим параллельно биологическому развитию человека и зависящим от возраста. Он протекает под влиянием целенаправленного обучения, которое содействует ускорению перехода к более высокому уровню. Отсутствие же обучения тормозит развитие. Обучение поэтому следует организовывать так, чтобы в связи с усвоением знаний о геометрических фигурах у детей развивалось и элементарное геометрическое мышление.
Познание геометрических фигур, их свойств и отношений расширяет кругозор детей, позволяет им более точно и разносторонне воспринимать форму окружающих предметов, что положительно отражается на их продуктивной деятельности (например, рисовании, лепке).
Большое значение в развитии геометрического мышления и про-странственных представлений имеют действия по преобразованию фигур (из двух треугольников составить квадрат или из пяти палочек сложить два треугольника).
Все эти разновидности упражнений развивают пространственные представления и начала геометрического мышления детей, формируют у них умения наблюдать, анализировать, обобщать, выделять главное, существенное и одновременно с этим воспитывают такие качества личности, как целенаправленность, настойчивость.
Итак, в дошкольном возрасте происходит овладение перцептивной и интеллектуальной систематизацией форм геометрических фигур. Перцептивная деятельность в познании фигур опережает развитие интеллектуальной систематизации.