что такое выбросы в данных
Что такое выбросы в данных
В рамках проектной деятельности, которую осуществляют участники тренинга шести сигм для зеленых поясов, часто приходится сталкиваться с нетривиальными задачами, решение которых не столь очевидно, а порой требует творческого подхода. Одной из таких задач является работа с выбросами перед расчетом описательных статистик и способности процесса на этапе измерений (Measure). В этой и ряде последующих публикаций попробуем разобраться в том, что такое выбросы и почему так важно знать о них, как они возникают и что с ними делать?
Итак, что же такое выбросы?
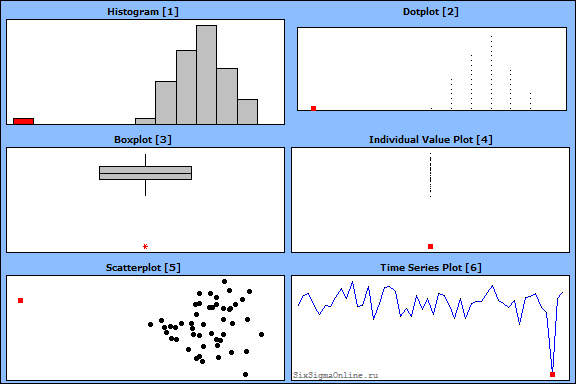
Выброс – это результат измерения, выделяющийся из общей выборки. Иными словами, выбросы – это необычно низкие или высокие значения наблюдаемой величины, причем настолько, что это заметно невооруженным глазом: в ходе графического анализа наблюдений вы можете заметить значения, которое не принадлежит популяции наблюдений. Определить выбросы можно с помощью: гистограмм [1], точечных [2] и ящичных [3] диаграмм, диаграмм индивидуальных значений [4], рассеяния [5] и даже диаграмм временных рядов [6]:
красные точки, звездочки и столбцы на диаграммах соответствуют выбросам
В теории статистического анализа нет однозначного критерия идентификации выбросов, и это – первая причина, по которой выбросы представляют опасность для неопытного исследователя.
Из определения следует, что все необычно низкие или высокие значения наблюдаемой величины могут быть выбросами. Как же определить, какое значение переменной является необычно высоким или низким. Один из самых простых способов: использовать диапазон трех стандартных отклонений вокруг среднего значения. Вероятность выхода величины за пределы ±3σ составляет 0,0027, а значит, с большой долей вероятности, значение, которое выходит за пределы ±3σ не принадлежит к популяции.
С другой стороны, можно привести ряд доводов против этого утверждения. Например, оно теряет смысл, если функция распределения отличается от нормальной или размер выборки слишком мал, чтобы представить генеральную совокупность значений. Кроме того, с вероятностью 0,0027 наблюдение все же может выйти за пределы диапазона трех стандартных отклонений.
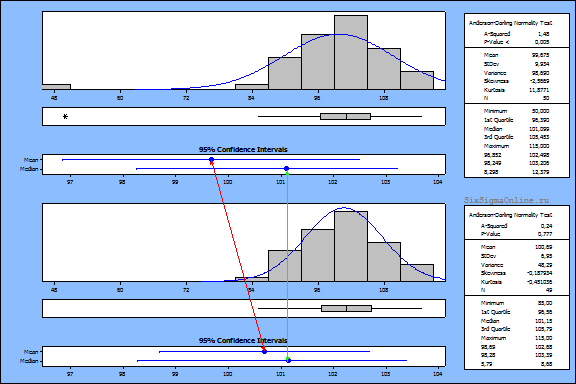
Вторая опасность, которую представляют выбросы – искажение статистик или результатов статистических расчетов. Такие показатели как среднее арифметическое (Mean), стандартное отклонение (StDev), асимметрия (Skewness), эксцесс (Kurtosis), а также критерий согласия с нормальным законом весьма подвержены влиянию выбросов. В отличие от среднего арифметического, медиана менее подвержена влиянию выбросов. На следующем рисунке медиана и среднее арифметическое до и после исключения выброса обозначены зеленой и красной стрелками соответственно:
Еще один классический пример – квартет Энскомба (Anscomb):
| X1 | Y1 | X2 | Y2 | X3 | Y3 | X4 | Y4 |
| 10 | 8,04 | 10 | 9,14 | 10 | 7,46 | 8 | 6,58 |
| 8 | 6,95 | 8 | 8,14 | 8 | 6,77 | 8 | 5,76 |
| 13 | 7,58 | 13 | 8,74 | 13 | 12,74 | 8 | 7,71 |
| 9 | 8,81 | 9 | 8,77 | 9 | 7,11 | 8 | 8,84 |
| 11 | 8,33 | 11 | 9,26 | 11 | 7,81 | 8 | 8,47 |
| 14 | 9,96 | 14 | 8,1 | 14 | 8,84 | 8 | 7,04 |
| 6 | 7,24 | 6 | 6,13 | 6 | 6,08 | 8 | 5,25 |
| 4 | 4,26 | 4 | 3,1 | 4 | 5,39 | 19 | 12,5 |
| 12 | 10,84 | 12 | 9,13 | 12 | 8,15 | 8 | 5,56 |
| 7 | 4,82 | 7 | 7,26 | 7 | 6,42 | 8 | 7,91 |
| 5 | 5,68 | 5 | 4,74 | 5 | 5,73 | 8 | 6,89 |
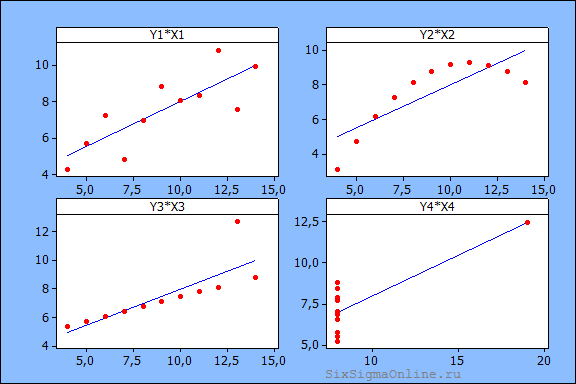
Квартет Энскомба – это четыре набора числовых данных, которые используют как свидетельство важности визуальной оценки наблюдений в корреляционном и регрессионном анализе:
Не смотря на различия взаимосвязи переменных X и Y, во всех четырех случаях статистические показатели, как и уравнение линейной регрессии, одинаковы:
| Характеристика | Значение |
| Среднее значение переменной X | 9.0 |
| Дисперсия переменной X | 10 |
| Среднее значение переменной Y | 7,5 |
| Дисперсия переменной Y | 3,75 |
| Коэффициент корреляции Пирсона | 0,816 |
| Уравнение линейной регрессии | Y=3+0.5X |
Обратите внимание на третий и четвертый наборы данных. Выброс в третьем примере искажает уравнение зависимости, а в четвертом – заставляет принять решение о наличии корреляции, в то время как ее на самом деле нет.
И, наконец, третья опасность, которую таят выбросы – это легкость их неверного истолкования, что, в свою очередь, приведет к неверному направлению последующего анализа. Наличие выбросов может означать ошибку ввода данных, недостаточную величину выборки или присутствие специальной причины отклонения – действие конкретного фактора или причины. Диагностируя выбросы, легко допустить ошибку, исключив нужные для анализа данные или наоборот – рассчитав показатели процесса, используя неверные результаты наблюдений.
Таким образом, существует, по меньшей мере, 3 причины, почему выбросы данных следует исследовать. Невнимательное отношение к выбросам наблюдений ставит под угрозу выводы о наблюдении процесса и ставит под угрозу результаты последующего анализа. Следовательно, обнаружив необычно низкие или высокие значения наблюдаемой величины, исследователь обязан найти причину их появления, прежде чем делать выводы о наблюдаемой переменной или приступать к последующему анализу данных. Наиболее вероятные причины появления выбросов будут рассмотрены в следующей статье.
Как использовать статистику для выявления выбросов в данных
Дата публикации 2018-04-25
При моделировании важно очистить выборку данных, чтобы убедиться, что наблюдения наилучшим образом представляют проблему.
Иногда набор данных может содержать экстремальные значения, которые выходят за пределы ожидаемого и отличаются от других данных. Они называются выбросами, и часто модели машинного обучения и навыки моделирования в целом могут быть улучшены путем понимания и даже устранения этих значений выбросов.
В этом руководстве вы узнаете больше о выбросах и двух статистических методах, которые можно использовать для идентификации и фильтрации выбросов из набора данных.
После завершения этого урока вы узнаете:
Обзор учебника
Этот урок разделен на 4 части; они есть:
Что такое выбросы?
Это редко, или отчетливо, или не подходит в некотором роде.
Выбросы могут иметь много причин, таких как:
Не существует точного способа определения и идентификации выбросов в целом из-за специфики каждого набора данных. Вместо этого вы или эксперт в области должны интерпретировать необработанные наблюдения и решить, является ли значение выбросом или нет.
Тем не менее, мы можем использовать статистические методы для выявления наблюдений, которые кажутся редкими или маловероятными с учетом имеющихся данных.
Это не означает, что указанные значения являются выбросами и должны быть удалены. Но инструменты, описанные в этом руководстве, могут помочь пролить свет на редкие события, которые могут потребовать второго взгляда.
Тестовый набор данных
Прежде чем мы рассмотрим методы идентификации выбросов, давайте определим набор данных, который мы можем использовать для тестирования методов.
Мы сгенерируем 10 000 случайных чисел из гауссовского распределения со средним значением 50 и стандартным отклонением 5.
Числа, взятые из гауссовского распределения, будут иметь выбросы. То есть в силу самого распределения будет несколько значений, которые будут далеки от средних, редких значений, которые мы можем определить как выбросы.
Мы будем использоватьrandn ()функция для генерации случайных гауссовских значений со средним значением 0 и стандартным отклонением 1, затем умножьте результаты на наше собственное стандартное отклонение и добавьте среднее значение для смещения значений в предпочтительный диапазон.
Генератор псевдослучайных чисел засеян, чтобы гарантировать, что мы получаем одну и ту же выборку чисел при каждом запуске кода.
При выполнении примера генерируется образец, а затем выводится среднее значение и стандартное отклонение. Как и ожидалось, значения очень близки к ожидаемым.
Метод стандартных отклонений
Если мы знаем, что распределение значений в выборке является гауссовским или гауссовидным, мы можем использовать стандартное отклонение выборки в качестве предела для выявления выбросов.
Гауссово распределение обладает свойством того, что стандартное отклонение от среднего может использоваться для надежного суммирования процентного значения в выборке.
Например, в пределах одного стандартного отклонения среднее будет охватывать 68% данных.
Таким образом, если среднее значение равно 50, а стандартное отклонение равно 5, как в тестовом наборе данных выше, то все данные в выборке между 45 и 55 будут составлять около 68% выборки данных. Мы можем охватить большую часть выборки данных, если расширим диапазон следующим образом:
Значение, которое выходит за пределы 3 стандартных отклонений, является частью распределения, но это маловероятное или редкое событие приблизительно в 1 из 370 выборок.
Давайте сделаем это на конкретном примере.
Иногда данные сначала стандартизируются (например, до Z-показателя с нулевым средним и единичной дисперсией), чтобы обнаружение выброса можно было выполнить с использованием стандартных значений отсечения Z-показателя. Это удобно и не требуется вообще, и мы сделаем вычисления в исходном масштабе данных здесь, чтобы прояснить ситуацию.
Мы можем рассчитать среднее и стандартное отклонение для данной выборки, а затем рассчитать порог для определения выбросов как более 3 стандартных отклонений от среднего.
Затем мы можем определить выбросы как те примеры, которые выходят за пределы определенных нижних и верхних пределов.
Кроме того, мы можем отфильтровать те значения из выборки, которые не находятся в определенных пределах.
Мы можем собрать все это вместе с нашим образцом набора данных, подготовленным в предыдущем разделе.
Полный пример приведен ниже.
Выполнение примера сначала выведет количество идентифицированных выбросов, а затем число наблюдений, которые не являются выбросами, демонстрируя, как идентифицировать и отфильтровать выбросы соответственно.
До сих пор мы говорили только об одномерных данных с гауссовым распределением, например одна переменная. Вы можете использовать тот же подход, если у вас есть многомерные данные, например, данные с несколькими переменными, каждая с разным распределением Гаусса.
Вы можете представить границы в двух измерениях, которые бы определяли эллипс, если у вас есть две переменные. Наблюдения, которые выходят за пределы эллипса, будут считаться выбросами. В трех измерениях это будет эллипсоид и т. Д. В более высокие измерения.
С другой стороны, если вы знали больше о домене, возможно, можно определить выброс, превышая пределы одного или подмножества измерений данных.
Межквартильный метод
Не все данные являются нормальными или достаточно нормальными, чтобы рассматривать их как взятые из гауссовского распределения.
Хорошей статистикой для суммирования выборки негауссовых распределений данных является Interquartile Range, или IQR для краткости.
IQR рассчитывается как разница между 75-м и 25-м процентилями данных и определяет прямоугольник на графике прямоугольника и вискера.
Мы называем процентили квартилями («кварта4) потому что данные делятся на четыре группы через 25-е, 50-е и 75-е значения.
IQR определяет средние 50% данных, или тело данных.
IQR может использоваться для определения выбросов путем определения пределов значений выборки, которые являются факторомКIQR ниже 25-го процентиля или выше 75-го процентиля. Общее значение для фактораКэто значение 1,5. Коэффициент k, равный 3 или более, можно использовать для определения значений, которые являются экстремальными выбросами или «дальние выходы”, Когда описано в контексте рамок и усов.
На графике бокса и усов эти пределы изображены в виде заборов на усиках (или линиях), которые нарисованы из бокса. Значения, которые выходят за пределы этих значений, отображаются в виде точек.
Мы можем рассчитать процентили набора данных, используяпроцентиля ()Функция NumPy, которая принимает набор данных и спецификацию желаемого процентиля. Затем IQR можно рассчитать как разницу между 75-м и 25-м процентилями.
Затем мы можем рассчитать пороговое значение для выбросов как 1,5-кратное IQR и вычесть это пороговое значение из 25-го процентиля и добавить его к 75-му процентилю, чтобы получить фактические пределы данных.
Затем мы можем использовать эти пределы для определения значений выбросов.
Мы также можем использовать пределы, чтобы отфильтровать выбросы из набора данных.
Мы можем связать все это вместе и продемонстрировать процедуру на тестовом наборе данных.
Полный пример приведен ниже.
При выполнении примера сначала выводятся идентифицированные 25-й и 75-й процентили и вычисленный IQR. Печатается число выявленных выбросов, а затем число наблюдений, не связанных с выбросами.
Подход может быть использован для многомерных данных путем расчета пределов для каждой переменной в наборе данных по очереди и с учетом выбросов в качестве наблюдений, которые выходят за пределы прямоугольника или гипер-прямоугольника.
расширения
В этом разделе перечислены некоторые идеи по расширению учебника, которые вы, возможно, захотите изучить.
Если вы исследуете какое-либо из этих расширений, я хотел бы знать.
Дальнейшее чтение
Этот раздел предоставляет больше ресурсов по теме, если вы хотите углубиться
Сообщений
статьи
Резюме
В этом руководстве вы обнаружили выбросы и два статистических метода, которые можно использовать для идентификации и фильтрации выбросов из набора данных.
В частности, вы узнали:
У вас есть вопросы?
Задайте свои вопросы в комментариях ниже, и я сделаю все возможное, чтобы ответить.
Необычные модели Playboy, или про обнаружение выбросов в данных c помощью Scikit-learn
Загрузка и первичный анализ данных
Итак, по-честному сославшись на первоисточник данных и человека, который над ними поработал, откроем CSV-файл с данными girls.csv и посмотрим, что там есть. Видим параметры 604-х девушек месяца Playboy с декабря 1953 по январь 2009: обхват груди (Bust, в см), обхват талии (Waist, в см), обхват бедер (Hips, в см), а также рост (Height, в см.) и вес (Weight, в кг).
Откроем нашу любимую среду программирования для Python (в моем случае Eclipse + PyDev) и загрузим данные с помощью библиотеки Pandas. В этой статье предполагается, что библиотеки Pandas, NumPy, SciPy, sklearn и matplotlib установлены. Если нет, пользователи Windows могут порадоваться и элементарно установить прекомпилированные библиотеки отсюда.
Ну а пользователям никсов и маков (как и автору) придется чуть-чуть помучаться, но статья не об этом.
Вначале импортируем модули, которые нам понадобятся. Об их роли будем говорить по мере поступления.
Создаем экземпляр girls структуры данных DataFrame модуля Pandas считыванием данных из файла girls.csv (он лежит рядом с данным py-файлом, иначе надо указывать полный путь). Параметр header говорит, что названия признаков находятся в первой строке (т.е. в нулевой, если считать, как программисты).
Кстати, Pandas — отличный вариант для тех, кто привык к питону, но все еще любит быстроту парсинга данных в R. Главное, что унаследовал Pandas от R — это как раз удобную структуру данных DataFrame.
Автор знакомился с Pandas по тьюториалу Kaggle в пробном соревновании «Titanic: Machine Learning from Disaster». Для тех, кто не знаком с Kaggle, — отличный повод наконец сделать это.
Посмотрим общую статистику наших девушек:
Нам сообщат, что в нашем распоряжении 604 девушки, каждая с 7-ю признаками — Month (тип object), Year (тип int64) и еще 5-ю признаками типа int64, которые мы уже называли.
Дальше узнаем про девушек побольше:
Эх, если бы в жизни все было так просто!
Интерпретатор нам перечислит основные статистические характеристики признаков девушек — среднее, минимальное и максимальное значения. Уже неплохо. Отсюда заключаем, что средние формы модели Playboy 89-60-88 (ожидаемо), средний рост — 168 см, вес — 52 кг.
Вот рост то, кажется, маловат. Видимо, объясняется тем, что данные исторические, с середины ХХ века, сейчас-то стандартом у моделей, кажется, считается рост 180 см.
Охват груди девушек меняется от 81 до 104 см, талия — от 46 до 89, бедра — от 61 до 99, рост — от 150 см до 188 см, вес — от 42 кг до 68 кг.
Ух ты, уже можно подозревать, что в данные вкралась ошибка. Это что за пивная бочка модель с талией 89 см? А как бедра могут быть 61 см?
Давайте посмотрим, что это за уникумы:
Это девушки месяца Playboy в декабре 1998-го и январе 2005-го соответственно. Несложно их отыскать здесь. Это тройняшки Николь, Эрика и Жаклин с неговорящей фамилей Дам (Dahm) — все три «под одним аккаунтом» и Дэстини Дэвис (Destiny Davis). Легко заметить, что талии тройняшек — 25 дюймов (64 см), а не 89, а бедра нашей Дэстини — 86 см, а никак не 61.
Для красоты можно еще построить и гистограммы распределения параметров девушек (для разнообразия они сделаны в R).

Итак, простым, невооруженным взглядом на данные уже можно найти в них какие-то странности, если, конечно, данных не очень много, и признаки можно как-то трактовать в понятном человеку виде.
Предобработка данных
Далее выделяем 2 главных компонента в данных, чтоб их можно было отобразить. Тут нам пригодилась библиотека Scikit-learn Principal Component Analysis (PCA). Также нам не помешает сохранить число наших девушек. Кроме того, мы скажем, что ищем 1% выбросов в данных, то есть ограничимся 6-7 «странными» девушками. (Переменные в Питоне, записанные в верхнем регистре, символизируют константы и обычно записываются в начале файла после подключения модулей).
Обучение модели
Для обнаружения «выбросов» в данных используем одноклассовую модель машины опорных векторов. Теоретическую работу над этой вариацией SVM начал Алексей Яковлевич Червоненкис. Как заявляет «Яндекс», сейчас разработка методов решения этой задачи занимает первое место в развитии теории машинного обучения.
Не буду здесь рассказывать, что такое SVM и ядра, про это и так много написано, например на Хабре (попроще) и на machinelearning.ru (посложнее). Отмечу только, что One-class SVM позовляет, как это следует из названия, отличать объекты одного класса. Обнаружение аномалий в данных — всего лишь скромное приложение этой идеи. Сейчас, в эпоху глубинного обучения, с помощью алгоритмов одноклассовой классификации пытаются научить компьютер «создавать представление» предмета, как, например, ребенок отличает собаку от всех остальных предметов.
Но вернемся к Scikit-реализации One-class SVM, которая неплохо документирована на сайте Scikit-learn.
Создаем экземпляр классификатора с гауссовым ядром и «скармливаем» ему данные.
Поиск выбросов
Создаем массив dist_to_border, который хранит расстояния от объектов обучающей выборки X до построенной разделяющей поверхности, а затем, после того, как мы выбрали порог, создаем массив индикаторов (True или False) того, что объект является представителем данного класса, а не выбросом. При этом расстояние положительно, если объект лежит «внутри» области, ограниченной построенной разделяющей поверхностью (т.е. является представителем класса), и отрицательно в противном случае. Порог определяется статистически, как такое расстояние до разделяющей поверхности, что у OUTLIER_FRACTION (в нашем случае у одного) процента выборки оно больше (т.е в нашем случае, threshold — это 1%-перцентиль массива расстояний до разделяющей поверхности).
Отображение и трактовка результатов
Наконец, визуализируем то что получилось. На этом моменте я не буду останавливаться, разобраться с matplotlib желающие могут самостоятельно. Это переработанный код из примера Scikit-learn «Outlier detection with several methods».
Получаем такую картинку:
Видны 7 «выбросов». Чтобы понять, что за девушки таятся под этим нелицеприятным «выбросы», посмотрим их в исходных данных.
А теперь самая занимательная часть — трактовка полученных выбросов.
Замечаем, что экспонатов в нашей кунсткамере всего 7 (мы так удачно задали порог OUTLIER_FRACTION), поэтому можно пройтись по каждому из них.
Примечательно, что дама с охватом бедер в 61 см, которую мы подозревали в сильном отличии от прочих девушек, по остальным параметрам вполне в норме, и SVM-ом не была определена как «выброс».
5 способов обнаружить выбросы / аномалии, которые должен знать каждый специалист по данным (код Python)
Дата публикации Mar 5, 2019
Что такое аномалия / выброс?
Например, вы можете ясно увидеть выбросы в этом списке: [20,24,22,19,29,18,4300, 30,18]
Это легко идентифицировать, когда наблюдения представляют собой просто набор чисел, и он одномерный, но когда у вас есть тысячи наблюдений или многомерных измерений, вам понадобятся более умные способы обнаружения этих значений. Это то, что эта статья будет освещать.
Почему мы заботимся об аномалиях?
Обнаружение выбросов или аномалий является одной из основных проблем интеллектуального анализа данных. Появляющееся расширение и продолжающийся рост данных и распространение устройств IoT заставляют нас переосмыслить подход к аномалиям и варианты использования, которые могут быть построены с учетом этих аномалий.
Теперь у нас есть умные часы и браслеты, которые могут определять сердцебиение каждые несколько минут. Обнаружение аномалий в данных сердцебиения может помочь в прогнозировании сердечных заболеваний. Аномалии в схемах движения могут помочь в прогнозировании аварий. Его также можно использовать для выявления узких мест в сетевой инфраструктуре и трафика между серверами. Следовательно, варианты использования и решения, основанные на обнаружении аномалий, безграничны.
Еще одна причина, по которой нам необходимо обнаруживать аномалии, заключается в том, что при подготовке наборов данных для моделей машинного обучения действительно важно обнаружить все выбросы и либо избавиться от них, либо проанализировать их, чтобы понять, почему они были у вас в первую очередь.
Теперь давайте рассмотрим 5 распространенных способов обнаружения аномалий, начиная с самого простого.
В статистике, если распределение данных приблизительно нормальное, то около 68% значений данных находятся в пределах одного стандартного отклонения от среднего, а около 95% находятся в пределах двух стандартных отклонений, иоколо 99,7%лежат в пределах трех стандартных отклонений
Поэтому, если у вас есть какая-либо точка данных, которая более чем в 3 раза превышает стандартное отклонение, то эти точки, скорее всего, будут аномальными или выбросами.
Давайте посмотрим код.
Графики представляют собой графическое изображение числовых данных через их квантили. Это очень простой, но эффективный способ визуализации выбросов. Думайте о нижнем и верхнем усиках как о границах распределения данных. Любые точки данных, которые показывают выше или ниже усов, могут считаться выбросами или аномальными. Вот код для построения прямоугольного графика:
Приведенный выше код отображает график ниже. Как вы можете видеть, он считает все, что выше 75 или ниже
-35, как выброс. Результаты очень близки к методу 1 выше.
Boxplot Анатомия:
Вывод вышеуказанного кода94.Это общее количество шумных точек. SKLearn помечает шумные точки как (-1). Недостатком этого метода является то, что чем выше размер, тем менее точным он становится. Вы также должны сделать несколько предположений, таких как оценка правильного значения дляEPS Wкоторый может быть сложным.
Этот метод работает по-другому. Он явно выделяет аномалии вместо того, чтобы профилировать и строить нормальные точки и области, назначая оценку каждой точке данных. Он использует тот факт, что аномалии являются точками данных меньшинства и что они имеют значения атрибутов, которые сильно отличаются от значений в обычных случаях. Этот алгоритм отлично работает с наборами данных очень большого размера, и он оказался очень эффективным способом обнаружения аномалий. Поскольку в этой статье основное внимание уделяется реализации, а не ноу-хау, я не буду подробно останавливаться на том, как работает алгоритм. Тем не менее, полная информация о том, как это работает, рассматривается в этомбумага,
Теперь давайте рассмотрим код:
Самое замечательное в этом алгоритме то, что он работает с данными очень большого размера. Он также может работать с потоковыми данными в режиме реального времени (встроенными в AWS Kinesis Analytics), а также с автономными данными.
Я объясняю концепцию более подробно в видео ниже:
В документе приведены некоторые показатели производительности по сравнению с Isolation Forest. Вот результаты из статьи, которая показывает, что RCF намного точнее и быстрее, чем Isolation Forests.
Полный пример кода можно найти здесь: