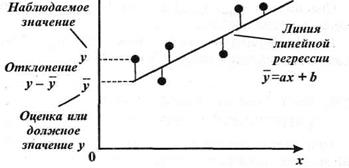
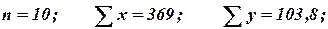что такое выборочное уравнение регрессии
Выборочное уравнение линейной регрессии. Метод наименьших квадратов
При проведении современных клинических исследований обычно нет недостатка в информации: каждому пациенту соответствует целое множество различных клинических показателей и данных.
В них могут быть завуалированы некоторые соотношения, основные черты которых и позволяют выявлять методы регрессионного анализа.
При этом задача регрессионного анализа состоит в подборе упрощенной аппроксимации этой связи с помощью математической модели.
Регрессионный анализ имеет в своем распоряжении специальные процедуры проверки, является ли выбранная математическая модель адекватной для описания имеющихся данных.
Чаще всего регрессионный анализ используется для прогноза, то есть предсказания значений ряда зависимых переменных по известным значениям других переменных.
Выше указывалось, что результаты наблюдений, приведенные в двумерной выборке:
| xi | x1 | x2 | x3 | x4 | x5 |
| yi | y1 | y2 | y3 | y4 | y5 |
можно представить в виде корреляционного поля точек (рис. 14.3), где каждая точка соответствует отдельным значениям х и у.
Рис. 14.3. Метод наименьших квадратов
В результате получается диаграмма рассеяния, позволяющая судить о форме и тесноте связи между варьирующими признаками. Довольно часто эта связь может быть аппроксимирована прямой линией (рис. 14.3).
В линейной математической модели уравнение линейной регрессии имеет вид:


Это эффективный метод, позволяющий уменьшить влияние ошибок измерений.
Теперь определяют должные величины 
Была исследована зависимость между ростом (X) и массой (Y), у 200 животных и рост, и масса подчиняются нормальному закону распределения. На рис. 3а видно, что эта зависимость линейная: чем больше рост, тем больше масса.
Из этой совокупности выберем выборку объема п = 10 (рис. 13.4б). Сохранилась ли эта зависимость массы от роста? На рис. 13.4б изображены 4 прямые, аппроксимирующие эту зависимость. Какую прямую можно считать наилучшей?
Рис 14.4. Зависимость между ростом (X) и массой (Y) у животных
Лучше прямые IIIи IV, а из них лучше та, которая ближе ко всем точкам выборки, то есть относительно которой разброс точек минимален.
Согласно методу наименьших квадратов лучше представляет зависимость 
По данным примера № 2:
| Xi | ||||||||||
| Yi | 7,8 | 8,3 | 7,6 | 9,1 | 9,6 | 9,8 | 11,8 | 12,1 | 14,7 | 13,0 |
Рассчитать параметры уравнения регрессии 
Именно это уравнение задает прямую IV в задаче № 6.
В примере № 2 был рассчитан коэффициент корреляции между ростом (X) и массой (Y) некоторых животных, ав примере № 7 было составлено уравнение линейной регрессии.
Как вы думаете, если поменять х и у, то изменится ли уравнение регрессии и коэффициент корреляции?
Провести корреляционно-регрессионный анализ. Построить корреляционное поле точек, проверить значимость (α ≤ 0,05) коэффициента корреляции между переменными X и Y и построить линию регрессии.
Изучали зависимость между содержанием вещества X в ткани С и приростом концентрации вещества Y в крови у пациентов, получавших препарат А.
Результаты наблюдений приведены в виде двумерной выборки объема 10:
| xi | 1,15 | 1,9 | 5,34 | 5,4 | 7,7 | 7,9 | 9,03 | 9,37 | 10,18 | |
| yi | 0,99 | 0,98 | 2,6 | 5,92 | 4,33 | 7,68 | 9,8 | 9,47 | 10,64 | 12,9 |
Результаты расчета на компьютере:
r = 0,94; tнабл = 6,17; 
Найдем из таблицы tкрит = 2,31; α ≤ 0,05;
Имеется очень сильная линейная корреляционная связь между признаками r = 0,94 (α ≥ 0,05).
Построим корреляционное поле точек (рис. 13.5).
Рис.13.5. График решения задачи 9
Рассчитаем должные величины:
при х = 1, 
Нанесем линию регрессии на график.
Нелинейная регрессия
Если график регрессии 
Выбор вида уравнения регрессии производится на основании опыта предыдущих исследований, литературных источников, профессионального мнения и визуального наблюдения расположения точек корреляционного поля. Этот очень важный этап анализа называется спецификацией.
Наиболее часто встречаются следующие виды уравнений нелинейной регрессии:




Для определения неизвестных параметров регрессии используется метод наименьших квадратов.
По данным таблицы исследовать зависимость урожайности зерновых культур Y (кг/га) от количества осадков X (см), выпавших в вегетационный период.
| n: | 15; |
| xi: | 53; |
| yi: | 25. |
Построить корреляционное поле точек и предположить наиболее подходящий вид уравнения регрессии.
Увеличение количества выпавших осадков приведет к увеличению урожайности до некоторого предела, после чего урожайность будет снижаться. Учитывая расположение точек корреляционного поля, можно предположить, что наиболее подходящим уравнением регрессии будет уравнение параболы.
Рис. 14.6. Нелинейная регрессия
Варианты заданий
► Провести корреляционно-регрессионный анализ:
построить корреляционное ноле точек;
проверить значимость (α ≤ 0,05) коэффициента корреляции между переменными Х и Y;
построить линию регрессии.
№ 14.1.Изучали зависимость между содержанием коллагена Y и эластина X в магистральных артериях головы (г/100 г сухого вещества, возраст 36-50 лет).
Результаты наблюдений приведены в виде двумерной выборки объема 5:
| xi: | 13,98 | 15,84 | 7,26 | 7,74 | 8,82; |
| yi: | 35,50 | 42,82 | 47,79 | 43,29 | 49,47. |
Результаты расчета на компьютере:
№ 14.2.Изучали зависимость между содержанием коллагена Y и эластина Х в магистральных артериях головы (г/100 г сухого вещества, возраст 51-75 лет).
Результаты наблюдений приведены в виде двумерной выборки объема 5:
| xi: | 13,50 | 13,09 | 6,45 | 7,26 | 8,80; |
| yi: | 33,97 | 38,07 | 53,98 | 46,00 | 48,61. |
Результаты расчета на компьютере:
№ 14.3.Изучали зависимость между систолическим давлением Y (мм рт. ст.) у мужчин в начальной стадии шока и возрастом X (годы). Результаты наблюдений приведены в виде двумерной выборки объема 11:
Результаты расчета на компьютере:
| xi: | 0,7 | 0,73 | 0,75 | 0,70 | 0,65 | 0,70 | 0,61 | 0,70 | 0,63; |
| yi: | 10,8 | 11,3 | 11,1 | 11,3 | 10,2 | 13,5 | 12. |
Результаты расчета на компьютере:
r = 0,02; mr = 0,38; tнабл = 0,05; 
№ 14.5.Изучали зависимость между суточной выработкой продукции на медицинском предприятии Y (т) и величиной основных производственных фондов X (млн руб).
Результаты наблюдений приведены в виде двумерной выборки объема 5:
| xi: | 25,5 | 29,5 | 31,9 | 35,4 | 39,2; |
| yi: | 25. |
Результаты расчёта на компьютере:
r = 0,74; tнабл = 7,62; 
№ 14.6.Изучали зависимость между объемом валовой продукции Y (млн руб) и среднесуточной численностью рабочих X. Результаты наблюдений приведены в виде двумерной выборки объема 5:
Результаты расчета на компьютере:
r = 0,8; tнабл = 6,2; 
№ 14.7.Изучали зависимость между минутным объемом сердца Y (л/мин) и средним давлением в левом предсердии X (см рт. ст.). Результаты наблюдений приведены в виде двумерной выборки объема 5:
| xi: | 4,8 | 6,4 | 9,3 | 11,2 | 17,7; |
| yi: | 0,4 | 0,69 | 1,29 | 1,64 | 2,4. |
Результаты расчета на компьютере:
r = 0,989; mr = 0,084; tнабл = 11,7; 
№ 14.8.Изучали зависимость между объемом Y (мкм 3 ) и диаметром Х (мкм) сухого эритроцита у млекопитающих. Результаты наблюдений приведены в виде двумерной выборки объема 9:
| xi: | 7,6 | 8,9 | 5,5 | 9,2 | 3,5 | 4,8 | 7,3 | 7,4 | 6,8; |
| yi: | 54. |
Результаты расчета на компьютере:
r = 0,96; mr = 0,12; tнабл = 7,99; 
№ 14.9.Изучали зависимость между количеством гемоглобина в крови (%) Y имассой животных X (кг). Результаты наблюдений приведены в виде двумерной выборки объема 9:
| xi: | 17,7 | 30; |
| yi: | 86. |
Результаты расчета на компьютере:
r = 0,64; mr = 0,29; tнабл = 2,2; 
№ 14.10.Изучали зависимость между массой тела гамадрилов-матерей X (кг) и их новорожденных детенышей Y (кг). Под наблюдением находилось 20 обезьян.
| xi: | 10,8 | 11,3 | 10,1 | 11,1 | 11,3 | 10,2 | 13,5 | 12,3 | ||
| 14,5 | 11,8 | 13,4 | 11,4 | 15,5 | 12,1; | |||||
| yi: | 0,7 | 0,73 | 0,75 | 0,7 | 0,65 | 0,65 | 0,7 | 0,61 | 0,7 | 0,63 |
| 0,7 | 0,65 | 0,72 | 0,69 | 0,78 | 0,7 | 0,6 | 0,85 | 0,8 | 0,75. |
Результаты расчета на компьютере:
r = 0,564; mr = 0,2; tнабл = 2,9; 

Результаты наблюдений приведены в виде двумерной выборки объема 5:
| xi: | 14,9 | 16,72 | 7,73 | 9,9 | 8,84; |
| yi: | 40,18 | 44,57 | 52,93 | 47,77 | 49,07. |
Результаты расчета на компьютере:
№ 14.12.Изучали зависимость между площадью поверхности тела Y (м 2 ) и ростом женщин Х (см). Результаты наблюдений приведены в виде двумерной выборки объема 11:
| xi: | 161; | ||||||||||
| yi: | 1,74 | 1,74 | 1,67 | 1,51 | 1,52 | 1,55 | 1,58 | 1,58 | 1,44 | 1,67 | 1,42. |
Результаты расчета на компьютере:
r = 0,145; mr = 0,4; tнабл = 0,44; 
№ 14.13.Изучали зависимость между поверхностью Y (мкм 2 ) и диаметром X (мкм) сухого эритроцита у млекопитающих.
Результаты наблюдений приведены в виде двумерной выборки объема 9:
| xi: | 7,6 | 8,9 | 5,5 | 9,2 | 3,5 | 4,8 | 7,3 | 7,4 | 6,8; |
| yi: | 144. |
Результаты расчета на компьютере:
r = 0,95; mr = 0,11; tнабл = 8,53; 
Приложение
t-распределение (распределение Стьюдента)
P (t > ta) = a и P (|t| > ta) = a
| k | Односторонняя критическая область (a) | |||||||
| 0,1 | 0,05 | 0,025 | 0,01 | 0,005 | 0,0025 | 0,001 | 0,0005 | |
| Двусторонняя критическая область (a) | ||||||||
| 0,2 | 0,1 | 0,05 | 0,02 | 0,01 | 0,005 | 0,002 | 0,001 | |
| ¥ | 3,08 1,89 1,64 1,53 1,48 1,44 1,41 1,40 1,38 1,37 1,36 1,36 1,35 1,34 1,34 1,34 1,33 1,33 1,33 1,33 1,32 1,32 1,32 1,32 1,32 1,32 1,31 1,31 1,31 1,31 1,30 1,30 1,29 1,28 | 6,31 2,92 2,35 2,13 2,02 1,94 1,89 1,86 1,83 1,81 1,80 1,78 1,77 1,76 1,75 1,75 1,74 1,73 1,73 1,72 1,72 1,72 1,71 1,71 1,71 1,71 1,70 1,70 1,70 1,70 1,68 1,67 1,66 1,64 | 12,71 4,30 3,18 2,78 2,57 2,45 2,36 2,31 2,26 2,23 2,20 2,18 2,16 2,14 2,13 2,12 2,11 2,10 2,09 2,09 2,8 2,07 2,07 2,06 2,06 2,06 2,05 2,05 2,05 2,04 2,02 2,00 1,98 1,96 | 31,82 6,96 4,54 3,75 3,36 3,14 3,00 2,90 2,82 2,76 2,72 2,68 2,65 2,62 2,60 2,58 2,57 2,55 2,54 2,53 2,52 2,51 2,50 2,49 2,49 2,48 2,47 2,47 2,46 2,46 2,42 2,39 2,36 2,33 | 63,66 9,92 5,84 4,60 4,03 3,71 3,50 3,36 3,25 3,17 3,11 3,05 3,01 2,98 2,95 2,92 2,90 2,88 2,86 2,85 2,83 2,82 2,81 2,80 2,79 2,78 2,77 2,76 2,76 2,75 2,70 2,66 2,62 2,58 | 127,32 14,09 7,45 5,60 4,77 4,32 4,03 3,83 3,69 3,58 3,50 3,43 3,37 3,33 3,29 3,25 3,22 3,20 3,17 3,15 3,14 3,12 3,10 3,09 3,08 3,07 3,06 3,05 3,04 3,03 2,97 2,91 2,85 2,81 | 318,30 22,33 10,21 7,17 5,89 5,21 4,79 4,50 4,30 4,14 4,02 3,93 3,85 3,79 3,73 3,69 3,65 3,61 3,58 3,55 3,53 3,51 3,48 3,47 3,45 3,44 3,42 3,41 3,40 3,39 3,31 3,23 3,16 3,09 | 636,61 31,60 12,92 8,61 6,87 5,96 5,41 5,04 4,78 4,59 4,44 4,32 4,22 4,14 4,07 4,02 3,97 3,92 3,88 3,85 3,82 3,79 3,77 3,75 3,73 3,71 3,69 3,67 3,66 3,65 3,55 3,46 3,37 3,29 |
Таблица значений функции
| x | ||||||||
| 0,0 | 0,00000 | |||||||
| 0,1 | ||||||||
| 0,2 | ||||||||
| 0,3 | ||||||||
| 0,4 | ||||||||
| 0,5 | ||||||||
| 0,6 | ||||||||
| 0,7 | ||||||||
| 0,8 | ||||||||
| 0,9 | ||||||||
| 1,0 | ||||||||
| 1,1 | ||||||||
| 1,2 | ||||||||
| 1,3 | ||||||||
| 1,4 | ||||||||
| 1,5 | ||||||||
| 1,6 | ||||||||
| 1,7 | ||||||||
| 1,8 | ||||||||
| 1,9 | ||||||||
| 2,0 | ||||||||
| 2,1 | ||||||||
| 2,2 | ||||||||
| 2,3 | ||||||||
| 2,4 | ||||||||
| 2,5 | ||||||||
| 2,6 | ||||||||
| 2,7 | ||||||||
| 2,8 | ||||||||
| 2,9 | ||||||||
| 3,0 | 0,49865 | 0,49865 | 3,1 | 3,2 | 3,3 | 3,4 | ||
| 3,5 | 3,6 | 3,7 | 3,8 | 3,9 | ||||
| 4,0 | — | — | — | — | — | — | — | — |
Критические значения выборочного коэффициента корреляции ra
Что такое выборочное уравнение регрессии
Отсюда выборочное уравнение регрессии будет иметь вид [c.168]
Выборочные уравнения регрессии [c.142]
Уравнение (5.4) определяет выборочное уравнение регрессии у на х. Сама функция J (x) называется выборочной регрессией Y на X, а график J (x) — выборочной регрессией. Аналогично определяется для случайных величин X [c.142]
Затем по формулам (3.7)— (3.15) находим выборочные характеристики и параметры уравнений регрессии [c.55]
Найдем дисперсию групповой средней у, представляющей выборочную оценку M Y). С этой целью уравнение регрессии (3.12) представим в виде [c.64]
Зная вектор Ь, выборочное уравнение множественной регрессии представим в виде [c.87]
Решение. По формуле (4.8) найдем вектор оценок параметров регрессионной модели b =(3,515 —0,006 15,542 60,110 4,475 —2,932), так что в соответствии с (4.9) выборочной уравнение множественной регрессии имеет вид [c.113]
Так что в соответствии с (4.9) выборочное уравнение множественной регрессии примет вид [c.120]
Так как параметры линейной регрессии зависимы между собой (b = Y — a-X ), то уравнение регрессии можно переписать в виде f = ax + b = a-(x — X + Y. Каждая точка на линии регрессии выражается через выборочные значения (а, 7), [c.120]
Регрессионное уравнение не дает точного прогноза зависимой переменной для любого заданного значения независимой переменной, так как коэффициенты регрессии подвержены случайным искажениям. Чтобы учесть погрешности оцененного уравнения регрессии, отражающего действительные закономерности поведения всего населения на основе выборочного наблюдения, уравнение регрессии обычно записывается как [c.5]
Наряду с ошибками спецификации могут иметь место ошибки выборки, поскольку исследователь чаще всего имеет дело с выборочными данными при установлении закономерной связи между признаками. Ошибки выборки имеют место и в силу неоднородности данных в исходной статистической совокупности, что, как правило, бывает при изучении экономических процессов. Если совокупность неоднородна, то уравнение регрессии не имеет практического смысла. Для получения хорошего результата обычно исключают из совокупности единицы с аномальными значениями исследуемых признаков. И в этом случае результаты регрессии представляют собой выборочные характеристики. [c.36]
Следует отметить, что вычисление и использование выборочных характеристик степени тесноты связи типа (1.21) затруднено по меньшей мере тремя обстоятельствами 1) необходимостью предварительного выбора общего вида регрессионной зависимости 2) необходимостью предварительного вычисления оценок для входящих в уравнение регрессии неизвестных параметров 3) отсутствием строгих рекомендаций по их проверке на статистическую значимость и по построению соответствующих интервальных оценок. [c.81]
Пользуясь результатами эксперимента, можно определить выборочные коэффициенты регрессии bo, bt, by, Ь, которые являются лишь оценками (приближенными значениями) для теоретических коэффициентов регрессии. Уравнение регрессии, полученное на основе опыта, запишется так [c.245]
Требуется по полученным данным найти выборочное уравнение прямой линии средней квадратической регрессии [c.143]
Как связаны эмпирические коэффициенты линейной регрессии с выборочным коэффициентом корреляции между переменными уравнения регрессии [c.107]
Проиллюстрируем связь между коэффициентом детерминации R для парного уравнения регрессии и выборочным коэффициентом корреляции гху. [c.134]
Если случайные отклонения уравнения регрессии удовлетворяют предпосылкам МНК, то ошибка предсказания At+p будет иметь нулевое математическое ожидание и минимальную дисперсию. При этом в случае парной регрессии (12.44) выборочная дисперсия определяется по формуле [c.294]
Коэффициенты регрессии, найденные исходя из системы нормальных уравнений, представляют собой выборочные оценки характеристики силы связи. Их несмещенность является желательным свойством, так как только в этом случае они могут иметь практическую значимость. Несмещенность оценки означает, что математическое ожидание остатков равно нулю. Следовательно, при большом числе выборочных оцениваний остатки не будут накапливаться и найденный параметр регрессии bt можно рассматривать как среднее значение из возможного большого количества несмещенных оценок. Если оценки обладают свойством несмещенности, то их можно сравнивать по разным исследованиям. [c.156]
Для простоты рассмотрим случай, когда набор активов У состоит из одного актива (т = 1), и перейдем к выборочному аналогу уравнения (15.23). Тогда, чтобы тестировать гипотезу Но, нам надо оценить коэффициенты регрессии [c.452]
Jf KXY vs x значит, прямая линия регрессии имеет уравнение у= У+(х— X )Kxv s2x Через KXy s2x обозначаем выборочные аналоги корреляционного момента случайной величины X, У и дисперсии соответственно. [c.136]
Несмотря на кажущуюся надежность уравнения регрессии для всей выборочной совокупности НГДУ, использовать его для практических целей нельзя, так как проверка на нормальность распределения у показала, что р=1,043 значительно больше табличного значения, что свидетельствует о ненормальном распределении у. Поэтому необходимо рассмотреть вопрос о правомерности использования данной совокупности НГДУ для корреляционного и регрессионного анализа. Для этого проведено попарное сравнение дисперсий о2 отдельных групп НГДУ. [c.88]
Полученные для выборочной совокупности НГДУ уравнения регрессии (20) — (22) могут точно не совпадать с истинной зависимостью, характерной для генеральной совокупности НГДУ. Поэтому необходимо найти доверительный интервал Д, в котором с определенной вероятностью будет находиться расчетная величина производительности труда. Для среднего значения производительности труда у величину доверительного интервала при заданной доверительной вероятности, являющейся минимальной, рассчитывают по формуле [c.89]
Зная величину Эу для каждого фактора, можно оценить возможный рост (падение) производительности труда за счет изменения отдельных факторов. Так, если нам известно, что изменение дебита скважин на 1 % приводит к изменению производительности труда на k %, то, зная величину изменения указанного фактора в планируемом периоде, можно рассчитать ожидаемый уровень производительности труда. Так как уравнения регрессии (20) — (22) выражают зависимость производительности труда от основных факторов не по каждому НГДУ, а в среднем по выборочной совокупности их, то прогнозируемые значения производительности труда целесообразно рассчитывать по формулам (20) — (22) лишь в отраслевом масштабе для отдельных групп НГДУ с растущей, стабильной или падающей добычей. [c.145]
Для точного описания уравнения регрессии необходимо знать условный закон распределения зависимой переменной Y при условии, что переменная X примет значение дс, т. е. Х=х. В статистической практике такую информацию получить, как правило, не удается, так как обычно исследователь располагает лишь выборкой пар значений (х/, у,) ограниченного объема п. В этом случае речь может идти об оценке (приближенном выражении, аппроксимаций) по выборке функции регрессии. Такой оценкой1 является выборочная линия (кривая) регрессии [c.52]
Проверка уравнения Фишера. Как ранее упоминалось, уравнение Фишера — это тождество, которое не может быть доказано или опровергнуто. Однако наблюдалось множество попыток ввести дополнительные ограничения для модели, чтобы проверить ее полезность для объяснения изменений процентных ставок во времени. Эти исследования восходят к работе самого Фишера, посвященной процентным ставкам и инфляции, где он обнаружил, что корреляция между темпами инфляции и ставкой по коммерческим бумагам оказалась низкой в обоих выборочных периодах (1890-1914 гг. и 1915-1927 гг.). Фама (Fama, 1975) предположил, что с течением времени серьезных изменений реальных ставок не происходит, поэтому данный процесс должен быть вызван исключительно изменениями в инфляции. Он протестировал данное положение, выстроив уравнение регрессии процентных ставок по отношению к ожидаемой инфляции [c.1193]
При практическом применении мнк-оценок исследователь часто сталкивается с явлением мультиколлинеарности, когда объясняющие переменные сильно коррелированы, т. е. существуют выраженные, хотя и неточные, линейные связи между несколькими или всеми объясняющими переменными. В этой ситуации точность обычных мнк-оценок резко падает ошибки некоторых параметров уравнения регрессии становятся очень большими, эти ошибки сильно скоррелированы, выборочные дисперсии резко возрастают. Резко сокращаются возможности интерпретации уравнения регрессии. Степень мультиколлинеарности измеряется либо обратной величиной минимального собственного числа нормированной (корреляционной) матрицы, либо числом обусловленности, равным отношению максимального собственного числа к минимальному. Если минимальное собственное число равно нулю, то степень мультиколлинеарности и число обусловленности являются бесконечно большими, и мы имеем дело с точной мультикол-линеарностью или вырожденной системой линейных уравнений. [c.297]