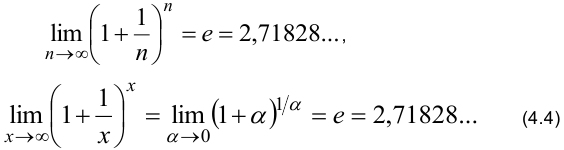что такое второй замечательный предел

Второй замечательный предел

В теории функций действительной переменной большую роль играют два замечательных предела и их следствия. Именно они позволяют доказать формулы производных простейших элементарных функций, то есть таблицу производных. Сам второй замечательный предел формулируется так:

Само доказательство этого предела проходит в несколько этапов. Полного доказательства мы здесь приводить не будем (оно есть во всех достаточно полных учебниках по математическому анализу), а дадим общую схему доказательства и доказательство первого этапа.

3. доказываем, что .

Из второго замечательного предела легко установить два важных следствия:

1)

Покажем, как из этих свойств получаются табличные производные.

Пример 1 Вывести формулу производной показательной функции .

Согласно определению производной функции имеем:

Теперь, используя правила дифференцирования и связь логарифмов с различными основаниями, находим: .

Пример 3 Найти предел .

Пример 4 Найти предел

.

Длины волн инфракрасного света достаточно велики, чтобы перемещаться сквозь облака, которые в противном случае блокировали бы наш обзор. Используя большие инфракра сные телескопы, астрономы смогли заглянуть в ядро нашей галактики. Большое количество звезд излучают часть своей электромагнитной энергии в виде видимого света, крошечной части спектра, к которой чувствительны наши глаза.

Так как длина волны коррелирует с энергией, цвет звезды говорит нам, насколько она горячая. Используя телескопы, чувствительные к различным диапазонам длин волн спектра, астрономы получают представление о широком круге объектов и явлений во вселенной.

Пример №1 Постройте центральную симметрию тетраэдра, относительно точки O, изображенных на рисунке 3.

Для построения такой центральной симметрии сначала проведем через все точки тетраэдра прямые, каждая из которых будет проходить через точку O. На них построим отрезки, удовлетворяющие условиям |AO|=|A?O|, |BO|=|B?O|, |CO|=|C?O|, |DO|=|D?O| Таким образом, и получим искомую симметрию (рис. 4).

В ряду разных механических движений особенным значением обладают колебания. Это движения и процессы, имеющие периодичность во времени.

В среде электромагнитных явлений также значительное место заняли электромагнитные колебания. В этих колебаниях заряды, токи, электрические и магнитные поля изменяются согласно периодическим законам.

Совет №1 Велосипедист, имеющий скорость 300 м/с, или идеальный газ, оказывающий давление 100 паскалей в большой тепловой машине — это странно.

Нужна помощь с курсовой или дипломной работой?

Источник

Первый замечательный предел

Первый замечательный предел часто применяется для вычисления пределов содержащих синус, арксинус, тангенс, арктангенс и получающихся при них неопределенностей ноль делить на ноль.

Формула

Для применения формулы необходимо, чтобы были соблюдены два условия:

Следствия

Достаточно редко в задания можно увидеть чистый первый замечательный предел, в котором можно сразу было бы записать ответ. На практике всё немного сложнее выглядит, но для таких случаев будет полезно знать следствия первого замечательного предела. Благодаря им можно быстро вычислить нужные пределы.

Примеры решений

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ$$ \lim_ \frac<\sin2x> <4x>=\frac<1> <2>$$Ответ$$ \lim_ \frac<\frac<\sin(x^2-9)>><\frac> = 1$$

Теперь видим в числителе и знаменателе появились выражения подходящие под формулу и следствия. Аргумент синуса и аргумент тангенса совпадают для соответствующих знаменателей

Ответ$$ \lim_ \frac<\sin2x> = \frac<2> <3>$$

В статье: «Первый замечательный предел, примеры решения» было рассказано о случаях, в которых целесообразно использовать данную формулу и её следствия.

Источник

Два замечательных предела

Первым замечательным пределом называют предел

Замечателен он тем, что раскрывает неопределенность вида 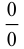, возникающую при вычислении пределов тригонометрических выражений.

Второй замечательный предел имеет несколько формулировок:

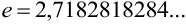
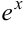
Число называется числом Непера. Оно лежит в основании натуральных логарифмов, показательной функции . Это иррациональное число, имеющее в математике значение не менее важное, чем число «пи».

Сам же предел замечателен тем, что раскрывает неопределенность вида 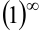, так как выражение в скобках стремится к единице. Доказательство замечательных пределов можно изучить в литературе.

Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:

Возможно вам будут полезны эти страницы:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник