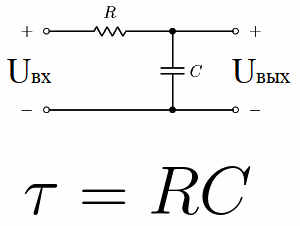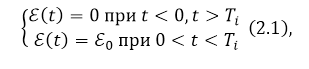что такое время релаксации в lr цепи

Содержание

Введение

На практике, однако, конденсаторы (и RC-цепи) обычно предпочтительнее катушек индуктивности, поскольку их легче изготовить и, как правило, они физически меньше, особенно для компонентов с более высокой стоимостью.

Обе цепи RC и RL образуют однополюсный фильтр. В зависимости от того, находится ли реактивный элемент (C или L) последовательно с нагрузкой или параллельно с нагрузкой, будет зависеть, является ли фильтр низкочастотным или высокочастотным.

Часто цепи RL используются в качестве источников питания постоянного тока для усилителей RF, где индуктивность используется для пропускания постоянного тока смещения и блокировки возврата RF в источник питания.

Комплексное сопротивление

Комплексное сопротивление Z _L (в омах ) от индуктора с индуктивностью L (в генри ) является

Собственные функции

В комплекснозначными собственные функции любого линейного времени инвариантной системы (LTI) имеют следующие формы:

Синусоидальное установившееся состояние

и оценка s становится

Последовательная схема

а напряжение на резисторе равно:

Текущий

Ток в цепи везде одинаковый, так как цепь включена последовательно:

Передаточные функции

Функция передачи к напряжению индуктора

Аналогично передаточная функция напряжения резистора равна

Передаточная функция по отношению к току равна

Полюсы и нули

Передаточные функции имеют один полюс, расположенный в

Коэффициент усиления и фазовый угол

Прирост по двум компонентам находится путем взятия величин из приведенных выше выражений:

Обозначение фазора

Эти выражения вместе могут быть заменены на обычное выражение для вектора, представляющего выходные данные:

Импульсивный ответ

Импульсная характеристика для напряжения индуктора равна

Точно так же импульсная характеристика для напряжения резистора равна

Ответ с нулевым входом

Реакция с нулевым входом (ZIR), также называемая естественной реакцией цепи RL, описывает поведение цепи после того, как она достигла постоянных напряжений и токов и отключена от любого источника питания. Это называется откликом с нулевым вводом, потому что он не требует ввода.

Рекомендации по частотной области

Решение вышеуказанного уравнения дает

это частота, которую фильтр будет ослаблять до половины своей исходной мощности.

Ясно, что фазы также зависят от частоты, хотя в целом этот эффект менее интересен, чем изменения усиления.

Таким образом, при постоянном токе (0 Гц ) напряжение резистора находится в фазе с напряжением сигнала, а напряжение индуктора опережает его на 90 °. По мере увеличения частоты напряжение на резисторе запаздывает на 90 ° относительно сигнала, а напряжение на катушке индуктивности становится синфазным с сигналом.

Замечания во временной области

Эти результаты также могут быть получены путем решения дифференциального уравнения, описывающего схему:

Первое уравнение решается с использованием интегрирующего коэффициента и дает ток, который необходимо дифференцировать, чтобы получить V _L ; второе уравнение простое. Решения точно такие же, как и полученные с помощью преобразований Лапласа.

Уравнение короткого замыкания

Для оценки короткого замыкания рассматривается цепь RL. Более общее уравнение:

С начальным состоянием:

я ( 0 ) знак равно я 0 <\ displaystyle i (0) = i_ <0>>

Что можно решить с помощью преобразования Лапласа :

Затем антитрансформация возвращается:

Если напряжение источника является ступенчатой ​​функцией Хевисайда (постоянный ток):

В случае, если напряжение источника является синусоидальной функцией (переменный ток):

Параллельная схема

Со сложными сопротивлениями:

Это показывает, что катушка индуктивности отстает от тока резистора (и источника) на 90 °.

Параллельная схема видна на выходе многих схем усилителя и используется для изоляции усилителя от эффектов емкостной нагрузки на высоких частотах. Из-за фазового сдвига, вносимого емкостью, некоторые усилители становятся нестабильными на очень высоких частотах и ​​имеют тенденцию к колебаниям. Это влияет на качество звука и срок службы компонентов (особенно транзисторов), и этого следует избегать.

Источник

4.2. Переходные процессы в RL-цепях

4.2. Переходные процессы в RL-цепях

Рассмотрим переходные процессы в RL-цепи на примере схемы, изображенной на рис. 4.1,а. Из рисунка видно, что переходные процессы в цепи будут возникать в моменты установки ключа К в положения 1 или 2.

При установке ключа в положение 1 происходит подключение к RL-цепи источника входного воздействия u(t) и начинается переходной процесс при нулевых начальных условиях. При установке ключа в положение 2 происходит отключение входного воздействия от цепи и замыкание индуктивностиL на резистор R и начинается переходной процесс при ненулевых начальных условиях.

Переходной процесс в RL-цепи при нулевых начальных условиях. Установим ключ К в положение 1 (рис. 4.1,а). При этом в цепи возникает ток i, который создает падения напряжений на R и L.

Рис. 4.1. RL-цепь (а) и переходные процессы в ней при подключении входного воздействия (б) и при отключеии входного воздействия(в).

Согласно второго закона Кирхгофа приложенное напряжение u(t) уравновешивается падениями напряжений на R и L, т.е.

u(t)=uR + uL = iR + Ldi/dt. (4.1)

Решение уравнения (4.1) можно записать в виде

где iсв – свободная составляющая тока, iпр – принужденная составляющая тока, обусловленная действием u(t).

Для определения свободной составляющей тока уравнение (4.1) необходимо приравнять к нулю, тогда будем иметь.

iсвR + Ldiсв/dt = 0. (4.3)

Выражение (4.3) является однородным дифференциальным уравнением, общее решение которого имеет вид

где τ = L/R [с] –постоянная времени RL-цепи.

Принужденную составляющую iпр найдем полагая, что u(t) = U = const, тогда в установившемся режиме iпр = U/R. Учитывая последнее выражение и (4.5) перепишем (4.2) в форме

До подключения к цепи входного напряжения ток в цепи был равен нулю, тогда на основании первого закона коммутации (4.6) будет иметь вид

Учитывая (4.7) находим закон изменения напряжения на индуктивности

uL = Ldi/dt = U ℮-t/τ. (4.8)

Графики зависимости i(t) и uL(t) изображены на рис. 4.1,б. Из рисунков и выражений (4.7) и (4.8) следует, что в момент подключения к индуктивности источника постоянного напряжения ток в цепи равен нулю, а напряжение на индуктивности достигает максимального значенияuL = U, т.е. индуктивность эквивалентна разрыву цепи.

С увеличением времени ток в цепи увеличивается, а напряжение uL уменьшается по экспоненциальному закону. При t = ∞ ток в цепи достигает максимального значения, а uL = 0, т.е. индуктивность эквивалентна короткозамкнутому участку цепи.

Из выражений (4.7) и (4.8) видно, что длительность переходного процесса зависит от постоянной времени цепи τ. Чем больше постоянная времени цепи τ, тем медленнее затухает переходной процесс. При t = τ напряжение UL уменьшается в е раз. На практике принято считать, что переходной процесс заканчивается через время t = 3τ, т.к. при этом ток (4.7) достигает 95% от своего установившегося значения.

Рассмотрим случай, когда на вход RL-цепи (рис. 4.1,а) подключается гармоническое колебание. Для этого случая принужденная составляющая тока будет

, (4.9)

где ; .

Свободная составляющая тока определятся выражением (4.5).

Постоянную интегрирования А определим исходя из начальных условий, т.е. при t = 0, i = 0, тогда на основании (4.2) запишем

. (4.10)

Напряжение на индуктивности определяется уравнением , т.е.

, (4.11)

Из (4.10) видно, что переходной процесс в RL-цепи при подключении ее к гармоническому колебанию, будет протекать по-разному в зависимости от момента включения входного воздействия. Если цепь будет подключена к источнику в момент, когдаφu = φ ± π/2, то в момент включения ток imax = 2Im, т.е. появляется бросок тока. При включении цепи в момент, когда φu = φ в цепи сразу наступает установившийся режим.

Переходной процесс в RL-цепи при ненулевых начальных условиях. Пусть к моменту коммутации ключ К на рис. 4.1,а находился в положении 1 и к RL-цепи было подключено напряжение u(t) = U = const. Следовательно в цепи была запасена энергия магнитного поля WL = LI2 = L(U/R)2. Установим ключ К в положение 2. При этом от цепи будет отключено входное воздействие и индуктивность L будет замкнута на резисторе R. В цепи возникает переходной процесс, описываемый уравнением

Принужденная составляющая тока iпр= 0. Решая уравнение (4.12) с учетом (4.3) – (4.5) находим

. (4.13)

В момент коммутации при t = 0 ток в цепи был i = U/R, поэтому из (4.13) имеем A = U/R. Подставляя полученное значение А в (4.13) будем иметь следующее выражение, описывающее изменение тока в RL-цепи после отключения входного воздействия

. (4.14)

Напряжение на индуктивности в переходном режиме изменяется по закону

. (4.15)

Графики изменения тока и напряжения изображены на рис. 4.1,в.

Из рисунков и выражений (4.14) и (4.15) видно, что при отключении от индуктивности входного воздействия и замыкании ее на резистор ток и напряжение стремятся к нулю. Это означает, что вся запасенная в индуктивности энергия с течением времени расходуется на тепловые потери в резисторе. Длительность переходного процесса зависит от постоянной времени цепи и переходной процесс заканчивается через времяt ≈ 3τ.

Источник

Переходные процессы в RC- и RL- цепях

Переходными, в электрической цепи, принято называть процессы возникающие в результате различных воздействий (например: включений или отключений цепи от источника питания, обрывах или коротких замыканиях, импульсных возмущающих воздействий и так далее) и переводящих её из одного стационарного (установившегося) состояния в новое (другое) стационарное состояние.

Рассмотрим переходный процесс в RC-цепи (рисунок 1), в состав которой входят резистор R, конденсатор С, ключ К и источник питания, на зажимах которого поддерживается постоянное напряжение E=U.

Рисунок 1. Схема RC-цепи.

Если установить ключ К в положение ”1” (рисунок 1), то начнётся процесс заряда конденсатора С через резистор R (рисунок 2,a). Для образовавшейся цепи будет справедливо соотношение :

Так как на конденсаторе напряжение скачком изменяться не может, то в момент (t=0) подключения цепи к источнику питания всё напряжение источника окажется на резисторе R, то есть u_R = U, u_c = 0.

В начальный момент времени заряда конденсатора, ток в RC-цепи будет иметь наибольшее значение: i=U/R. Конденсатор начнёт заряжаться, напряжение на нём “постепенно” повышается, что, в свою очередь, приведёт к уменьшению падения напряжения на резисторе u_R = U — u_C, а следовательно и уменьшению тока в RC-цепи, вплоть до его ”полного” прекращения. Напряжение на конденсаторе, во время заряда, нарастает по экспоненциальной зависимости согласно формуле:

где t – любой момент времени, τ – постоянная времени заряда конденсатора в секундах:

Значения напряжения на резисторе и общего тока RC-цепи уменьшаются также по экспоненциальному закону:

Рисунок 2. Переходные процессы в RC-цепи. (а – при подключении к источнику; б –при замыкании цепи)

Поэтому, принято считать, что процесс заряда конденсатора заканчивается, когда напряжение на нём достигает значений 90,95 или 99% величины напряжения источника питания U=E.

В подавляющем большинстве случаев, как на практике, так и в теоретических расчётах, время t в течение которого конденсатор считается полностью заряженным, принимают равным 3τ. Также это можно отнести ко всем электрическим цепям, где токи меняются по экспоненциальному закону.

Ток в начальный момент ( t=0) разряда конденсатора будет иметь максимальное значение:

Но по мере разряда конденсатора (превращения накопленной в его электрическом поле энергии в тепловую на резисторе R ) напряжение на нём будет уменьшаться и, как следствие, будут уменьшаться по экспоненциальному закону ток в цепи и напряжение на резисторе:

Через некоторое время, например t=3τ (см. приведенную выше табл.), на конденсаторе останется примерно 5% напряжения от начального значения, что условно можно считать окончанием переходного процесса и возвратом схемы в исходное состояние когда: u_C = 0, u_R = 0, i = 0.

Теперь рассмотрим переходной процесс в RL-цепи (рис.3), в состав которой входят резистор R, катушка индуктивности L, ключ К и источник питания, на зажимах которого поддерживается постоянное напряжение E=U.

Рисунок 3. Схема RL-цепи.

где τ – постоянная времени RL-цепи,

Рисунок 4. Переходные процессы в RL-цепи.
(а – при подключении к источнику; б –при замыкании цепи)

На рисунке 4,а показано что ток в цепи, особенно в начале подключения к источнику, нарастает с наибольшей скоростью, но уже при t= τ его рост значительно замедляется, а при t=3τ практически прекращается и можно считать что его величина достигла установившегося значения i=U/R. При этом, с ростом тока, ЭДС самоиндукции уменьшается до нуля, переходной процесс заканчивается.

Источник

Природе свойственны периодические процессы: день сменяет ночь, теплое время года сменяется холодным и т. д. Период этих событий почти постоянен и поэтому может быть строго определен. Кроме того, мы вправе утверждать, что приведенные в качестве примера периодические природные процессы не являются затухающими, по крайней мере по отношению к продолжительности жизни одного человека.

Сплошь и рядом в электротехнике можно встретить так называемые экспоненциальные переходные процессы, суть которых заключается в том, что система просто стремится придти к какому-то равновесному состоянию, которое в конце концов выглядит как состояние покоя. Такой переходный процесс может быть как нарастающим, так и спадающим.

Внешняя сила сначала выводят динамическую систему из состояния равновесия, а затем не препятствует естественному возврату данной системы к ее исходному состоянию. Эта последняя фаза и есть так называемый переходный процесс, которому свойственна определенная длительность. Кроме того процесс выведения системы из равновесия также является переходным процессом с характерной длительностью.

Так или иначе, постоянной времени переходного процесса мы называем его временную характеристику, определяющую время, через которое некоторый параметр данного процесса изменится в «е» раз, то есть увеличится или уменьшится примерно в 2,718 раз по сравнению с состоянием, принятым за исходное.

Рассмотрим для примера электрическую цепь, состоящую из источника постоянного напряжения, конденсатора и резистора. Подобного рода цепь, где резистор включен последовательно с конденсатором, называется интегрирующей RC-цепью.

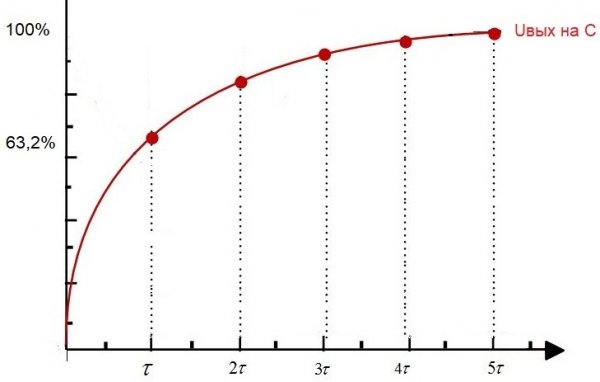
Если в начальный момент времени подать на такую цепь питание, то есть установить на входе некоторое постоянное напряжение Uвх, то Uвых — напряжение на конденсаторе, начнет по экспоненте нарастать.

Через время t1 напряжение на конденсаторе достигнет 63,2% от напряжения на входе. Так вот, промежуток времени от начального момента до t1 – это и будет постоянная времени данной RC-цепи.

Данную константу цепи называют «тау», она измеряется в секундах, а обозначают ее соответствующей греческой буквой. Численно для RC-цепи она равна R*C, где R выражается в омах, а С — в фарадах.

Интегрирующие RC-цепи применяются в электронике в качестве фильтров нижних частот, когда более высокие частоты необходимо отсечь (подавить), а более низкие — пропустить.

Практически механизм такой фильтрации зиждиться на следующем принципе. Для переменного тока конденсатор выступает как емкостное сопротивление, значение которого обратно пропорционально частоте, то есть чем выше частота — тем меньшим будет реактивное сопротивление конденсатора в омах.

Следовательно, если пропустить через RC-цепь переменный ток, то, как на плечах делителя напряжения, на конденсаторе упадет определенное напряжение, пропорциональное его емкостному сопротивлению на частоте пропускаемого тока.

Если известна частота среза и амплитуда входного переменного сигнала, то для разработчика не составит труда подобрать такие конденсатор и резистор в RC-цепь, чтобы минимальное (граничное) напряжение (для частоты среза — верхней частотной границы) приходилось на конденсатор как на реактивное сопротивление, входящее в состав делителя в совокупности с резистором.

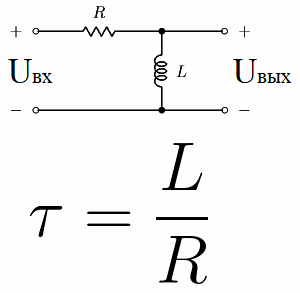
Теперь рассмотрим так называемую дифференцирующую цепь. Это цепь, состоящая из последовательно соединенных резистора и катушки индуктивности, RL-цепь. Ее постоянная времени численно равна L/R, где L – индуктивность катушки в генри, а R – сопротивление резистора в омах.

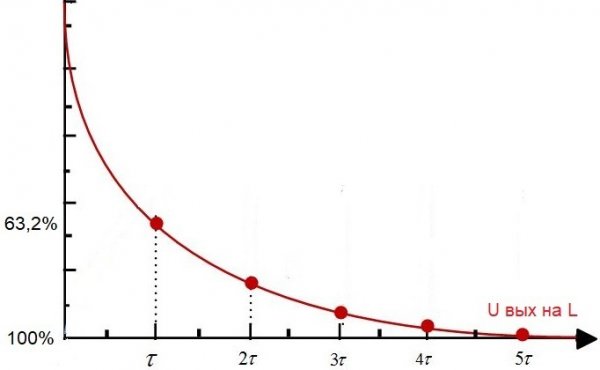
Если к такой цепи приложить постоянное напряжение от источника, то через время тау напряжение на катушке уменьшится по сравнению с U вх на 63,2%, то есть в полном соответствии со значением постоянной времени для данной электрической цепи.

В цепях переменного тока (переменных сигналов) LR-цепи применяются в качестве фильтров верхних частот, когда низкие частоты необходимо отсечь (подавить), а частоты выше (выше частоты среза — нижней частотной границы)— пропустить. Так вот, индуктивное сопротивление катушки тем больше, чем выше частота.

Как и в случае с рассмотренной выше RC-цепью, здесь используется принцип делителя напряжения. Ток более высокой частоты, пропускаемый через RL-цепь, вызовет большее падение напряжения на индуктивности L, как на индуктивном сопротивлении, входящем в состав делителя напряжения в совокупности с резистором. Задача разработчика — подобрать такие R и L, чтобы минимальное (граничное) напряжение на катушке получалось как раз на частоте среза.

Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!

Источник

Переходные процессы в RC и LC цепях

Вы будете перенаправлены на Автор24

Переходными процессами, возникающими в электрических цепях, называют явления (процессы), которые происходят в них после того как один из параметров испытал быстрое изменение. Например, включение и выключение ЭДС в цепи с сопротивлением и индуктивностью.

RC цепь

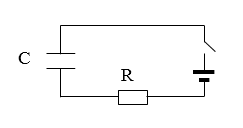
RC цепью называется электрическая цепь, которая состоит из конденсатора (конденсаторов) (емкость C), сопротивления (сопротивлений) (R) и источника ЭДС (рис.1). В такой цепи могут происходить только релаксационные непериодические процессы.

Присутствие в цепи конденсатора исключает возможность существования в ней постоянного тока. Разность потенциалов между обкладками конденсатора полностью компенсирует действие сторонней ЭДС (источника). Переменный же ток в такой сети возможен благодаря переменному заряду на конденсаторе. Разность потенциалов на обкладках не компенсирует действия сторонней ЭДС, в результате чего поддерживается некоторая сила тока.

Закон Ома для RC цепи имеет вид:

Включение (выключение) постоянной ЭДС в RC цепи

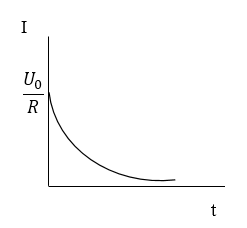
Допустим, что постоянное напряжение ($U_0$) включают в момент времени, который мы принимаем за начальный ($t=0$). Из уравнения (1) следует, что:

Решением уравнения (4) при заданном начальном условии (3) является функция:

Готовые работы на аналогичную тему

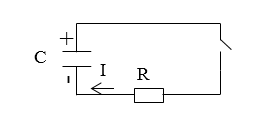
Если в RC цепи емкость конденсатора велика, то ток после того как выключили источник постоянного напряжения может течь в цепи продолжительное время. Если в цепь включить лампу, то она сначала вспыхнет, за тем постепенно погаснет.

LC цепь

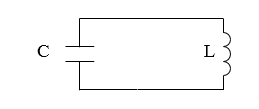
$LC$ цепью называют цепь, которая состоит из катушки индуктивности и емкости (рис.3).

Составили цепь из катушки и заряженного конденсатора. Конденсатор начнет разряжаться, в контуре возникнет ток. При этом энергия электрического поля уменьшается, энергия магнитного поля, которое порождается током, который течет через индуктивность, растет. Энергия магнитного поля ($W_m$) равна:

Уравнение колебаний в контуре без активного сопротивления

Решение:

Используем второе правило Кирхгофа, запишем, что после того как ключ в цепи замкнули, выполняется равенство:

\[U_R=RI_R,\ I_C=C\frac