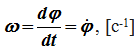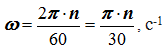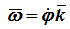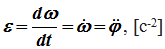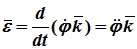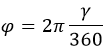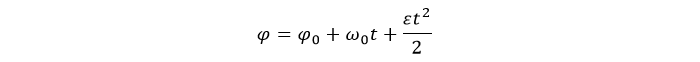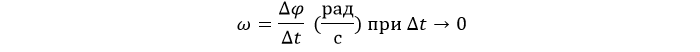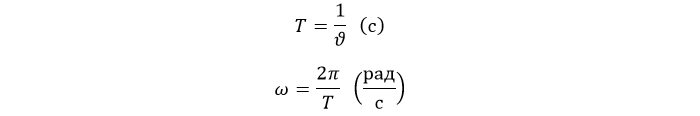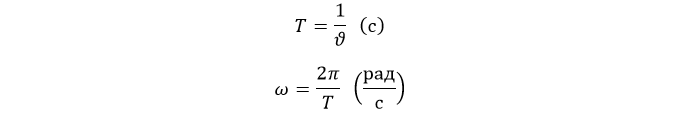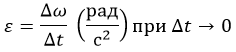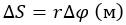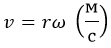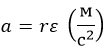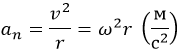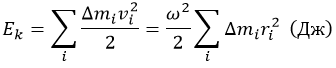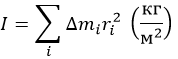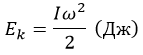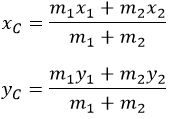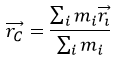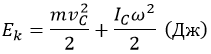что такое вращательное движение твердого тела
Поступательное и вращательное движение
Движение твердого тела разделяют на виды:
Первые два из них – простейшие, а остальные представляют как комбинацию основных движений.
Поступательное криволинейное движение. Угол поворота тела
Поступательным называют движение твердого тела, при котором любая прямая, проведенная в нем, двигается, оставаясь параллельной своему начальному направлению.
Прямолинейное движение является поступательным, но не всякое поступательное будет прямолинейным. При наличии поступательного движения путь тела представляют в виде кривых линий.
Свойства поступательного движения определяются теоремой: при поступательном движении все точки тела описывают одинаковые траектории и в каждый момент времени обладают одинаковыми по модулю и направлению значениями скорости и ускорения.
Следовательно, поступательное движение твердого тела определено движением любой его точки. Это сводится к задаче кинематики точки.
Понятие о скорости и ускорении тела имеют смысл только при наличии поступательного движения. В других случаях точки тела характеризуются разными скоростями и ускорениями.
Вращательное движение абсолютно твердого тела вокруг неподвижной оси – это движение всех точек тела, находящихся в плоскостях, перпендикулярных неподвижной прямой, называемой осью вращения, и описывание окружностей, центры которых располагаются на этой оси.
При наличии такого вращения значения углов поворота радиус-вектора различных точек тела будут аналогичны.
Вращательное и поступательное движение. Формулы
| Поступательное | Вращательное |
| Равномерное | |
| s = υ · t | φ = ω · t |
| υ = c o n s t | ω = c o n s t |
| a = 0 | ε = 0 |
| Равнопеременное | |
| s = υ 0 t ± a t 2 2 | φ = ω 0 t ± ε · t 2 2 |
| υ = υ 0 ± a · t | ω = ω 0 ± ε · t |
| a = c o n s t | ε = c o n s t |
| Неравномерное | |
| s = f ( t ) | φ = f ( t ) |
| υ = d s d t | ω = d φ d t |
| a = d υ d t = d 2 s d t 2 | ε = d ω d t = d 2 φ d t 2 |
Задачи на вращательное движение
Решение
Решение
iSopromat.ru
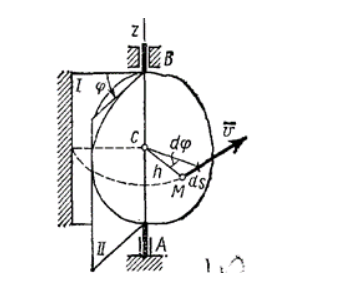
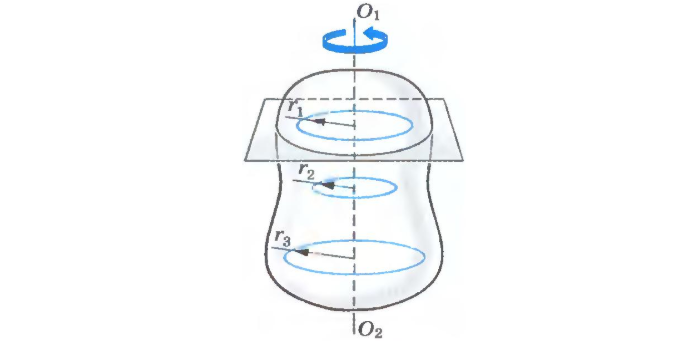
Вращательное движение твердого тела – это движение, при котором тело имеет как минимум две неподвижные точки (рисунок 1.3). Прямая, проходящая через эти точки, называется осью вращения.
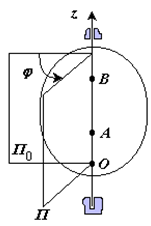
Положение тела определено, если задан угол φ между плоскостями П0 и П, одна из которых неподвижна, а другая жестко связана с телом.
φ=φ(t) – уравнение вращательного движения твердого тела.
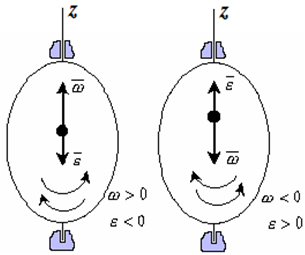
За положительное направление отсчета принимается вращение против хода часовой стрелки, если смотреть навстречу положительному направлению оси z.
Траекториями точек тела при его вращении вокруг неподвижной оси являются окружности, расположенные в плоскостях, перпендикулярных оси вращения.
Для характеристики изменения угла поворота с течением времени вводится величина, называемая угловой скоростью ω:
Вектор угловой скорости – это вектор, направленный по оси вращения в ту сторону, откуда вращение видно происходящим против хода часовой стрелки, с модулем, равным модулю алгебраической угловой скорости
где k – единичный вектор оси вращения.
Угловое ускорение – мера изменения угловой скорости:
Вектор углового ускорения – производная вектора угловой скорости по времени (рис. 1.4)
представляют совокупность основных формул вращательного равнопеременного движения тела.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Вращательное движение твердого тела: уравнение, формулы
В природе и технике мы часто сталкиваемся с проявлением вращательного движения твердых тел, например, валов и шестерен. Как в физике описывают этот тип движения, какие формулы и уравнения для этого применяются, эти и другие вопросы освещаются в данной статье.
Что такое вращение?

Чтобы вращение происходило, должно существовать центростремительное ускорение, которое возникает за счет центростремительной силы. Эта сила направлена от центра масс тела к оси вращения. Природа центростремительной силы может быть самой разной. Так, в космическом масштабе ее роль выполняет гравитация, если тело закреплено нитью, то сила натяжения последней будет центростремительной. Когда тело вращается вокруг собственной оси, роль центростремительной силы играет внутреннее электрохимическое взаимодействие между составляющими тело элементами (молекулами, атомами).

Необходимо понимать, что без присутствия центростремительной силы тело будет двигаться прямолинейно.
Описывающие вращение физические величины
Во-первых, это динамические характеристики. К ним относятся:
Во-вторых, это кинематические характеристики. Перечислим их:
Кратко опишем каждую из названных величин.
Момент импульса определяется по формуле:
Момент инерции материальной точки рассчитывается с помощью выражения:
Для любого тела сложной формы величина I рассчитывается, как интегральная сумма моментов инерции материальных точек.
Момент силы M вычисляется так:
Физический смысл всех величин, в названии которых присутствует слово «момент», аналогично смыслу соответствующих линейных величин. Например, момент силы показывает возможность приложенной силы сообщить угловое ускорение системе вращающихся тел.
Кинематические характеристики математически определяются следующими формулами:
Как видно из этих выражений, угловые характеристики аналогичны по своему смыслу линейным (скорости v и ускорению a), только они применимы для круговой траектории.
Динамика вращения
В физике изучение вращательного движения твердого тела осуществляется с помощью двух разделов механики: динамики и кинематики. Начнем с динамики.
Динамика изучает внешние силы, действующие на систему вращающихся тел. Сразу запишем уравнение вращательного движения твердого тела, а затем, разберем его составные части. Итак, это уравнение имеет вид:
Момент силы, который действует на систему, обладающую моментом инерции I, вызывает появление углового ускорения α. Чем меньше величина I, тем легче с помощью определенного момента M раскрутить систему до больших скоростей за малые промежутки времени. Например, металлический стержень легче вращать вдоль его оси, чем перпендикулярно ей. Однако, тот же стержень легче вращать вокруг оси, перпендикулярной ему, и проходящей через центр масс, чем через его конец.
Закон сохранения величины L
Выше была введена эта величина, она называется моментом импульса. Уравнение вращательного движения твердого тела, представленное в предыдущем пункте, часто записывают в иной форме:
Если момент внешних сил M действует на систему в течение времени dt, то он вызывает изменение момента импульса системы на величину dL. Соответственно, если момент сил равен нулю, тогда L = const. Это и есть закон сохранения величины L. Для нее, используя связь между линейной и угловой скоростью, можно записать:
Таким образом, при отсутствии момента сил произведение угловой скорости и момента инерции является постоянной величиной. Этот физический закон используют фигуристы в своих выступлениях или искусственные спутники, которые необходимо повернуть вокруг собственной оси в открытом космосе.
Центростремительное ускорение
Выше, при изучении вращательного движения твердого тела, уже была описана эта величина. Также была отмечена природа центростремительных сил. Здесь лишь дополним эту информацию и приведем соответствующие формулы для расчета этого ускорения. Обозначим его ac.
Поскольку центростремительная сила направлена перпендикулярно оси и проходит через нее, то момента она не создает. То есть эта сила не оказывает совершенно никакого влияния на кинематические характеристики вращения. Тем не менее, она создает центростремительное ускорение. Приведем две формулы для его определения:
Таким образом, чем больше угловая скорость и радиус, тем большую силу следует приложить, чтобы удержать тело на круговой траектории. Ярким примером этого физического процесса является занос автомобиля во время поворота. Занос возникает, если центростремительная сила, роль которой играет сила трения, становится меньше, чем центробежная сила (инерционная характеристика).
Кинематика вращения
Три основные кинематические характеристики были перечислены выше в статье. Кинематика вращательного движения твердого тела формулами следующими описывается:
θ = ω*t => ω = const., α = 0;
θ = ω0*t + α*t2/2 => ω = ω0 + α*t, α = const.
В первой строке приведены формулы для равномерного вращения, которое предполагает отсутствие внешнего момента сил, действующего на систему. Во второй строке записаны формулы для равноускоренного движения по окружности.
Отметим, что вращение может происходить не только с положительным ускорением, но и с отрицательным. В этом случае в формулах второй строки следует перед вторым слагаемым поставить знак минус.
Пример решения задачи
На металлический вал в течение 10 секунд действовал момент силы 1000 Н*м. Зная, что момент инерции вала равен 50 кг*м2, необходимо определить угловую скорость, которую придал валу упомянутый момент силы.
Применяя основное уравнение вращения, вычислим ускорение вала:
Поскольку это угловое ускорение действовало на вал в течение времени t = 10 секунд, то для вычисления угловой скорости применяем формулу равноускоренного движения:
Здесь ω0 = 0 (вал не вращался до действия момента сил M).
Подставляем в равенство численные значения величин, получаем:
ω = 1000/50*10 = 200 рад/с.
Чтобы это число перевести в привычные обороты в секунду, необходимо его поделить на 2*pi. Выполнив это действие, получаем, что вал будет вращаться с частотой 31,8 об./с.
Вращательное движение твердого тела – движение, при котором все точки объекта описывают траекторию в виде окружности.
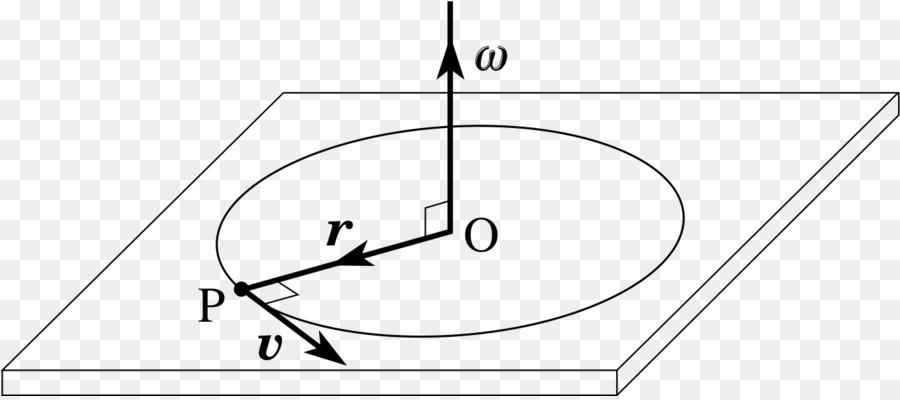
Распространенный случай в физике – вокруг покоящейся оси (рис. 1).
Рис. 1 Вращение твердого тела вокруг оси
Линия, соединяющая неподвижные точки, читается осью вращения. Кинематика перемещения в целом аналогична поступательной. Только путь измеряется не в метрах, а в радианах или градусах.
Последние связаны между собой следующей формулой:
ϕ – угол в радианах (рад);
γ – угол в градусах (°).
Закон и уравнение вращательного движения твердого тела
Законы движения также схожи. Для равноускоренного движения:
ϕ0 – начальный угол (рад);
ω0 – начальная угловая скорость (рад/с);
ε – угловое ускорение (рад/с 2 ).
Под положительным понимают перемещение против часовой стрелки.
Угловая скорость
В обычной жизни вращение оценивается в оборотах за единицу времени. За минуту чаще всего. Для расчетов такие характеристики неудобны. Поэтому определяется так:
Скорость в оборотах ν легко связать с угловой:
ν – скорость в оборотах (1/с).
Используется еще одна важная величина – период вращения T. За это время предмет совершает полный поворот:
Угловое ускорение
В уравнении движения был показан частный случай равноускоренного перемещения. Но это не всегда так. Также ε может принимать отрицательные значения в случае замедления.
Линейные величины
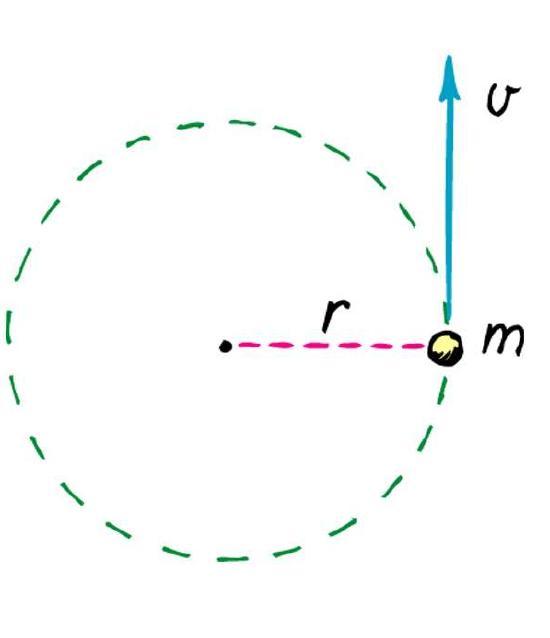
При малых величинах пройденный путь (см. рис. 2) будет равен:
где r – расстояние до центра вращения (м).
Откуда следует линейная скорость:
Вектор, перпендикулярный отрезку, r. То есть расположенный на касательной к окружности вращения.
И, соответственно, ускорение:
Кроме того, передвижение по кривой линии невозможно без центростремительного ускорения:
Возвратно-вращательное движение
Общий случай раскачивания маятника. Анализ подобных противоположных телодвижений пары объектов порождает некоторые парадоксы.
Возникают странные и дико звучащие названия вроде «безопорного движителя». Выводы в конечном итоге противоречат законам механики Ньютона.
Приверженцы таких рассуждений существуют и доводы имеют право на жизнь. Не все общепринятые взгляды безупречны. Евклидова геометрия тому пример. Теория довольно запутана, и здесь мы ее рассматривать не будем.
С учетом масс
Представив себе, что тело состоит из незначительных масс mi, получим любопытные результаты. Кинетическая энергия выразится так:
Джоуль (Дж) – единица энергии и работы в системе СИ.
Моментом инерции относительно выбранной оси называется:
или в соответствующей интегральной форме.
Тогда энергия выразится следующим образом:
То есть имеется некий аналог массы. Но последняя является неизменной присущей объекту величиной. Момент же инерции зависит от местонахождения оси.
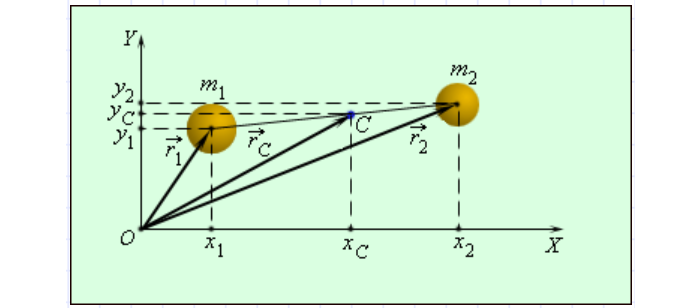
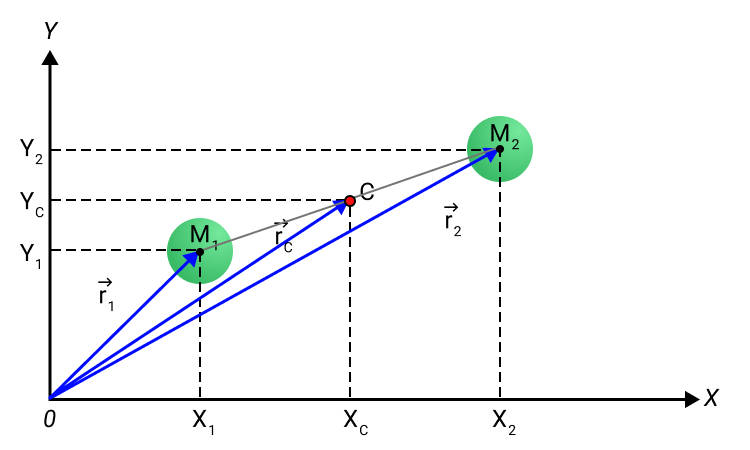
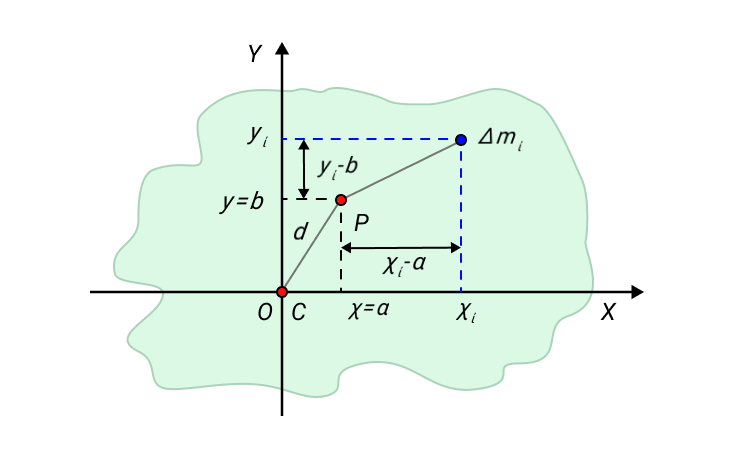
В реальных условиях распространен случай вращения вокруг оси, включающей центр масс. Найдем его для системы, указанной на рис. 3.
Рис. 3 Определение центра масс.
Определится по формулам:
Вектор, направленный из начала координат в центр масс, в общем случае выразится следующим образом:
Можно перевести в интегральную форму. В присутствии гравитации – заодно и центр тяжести.
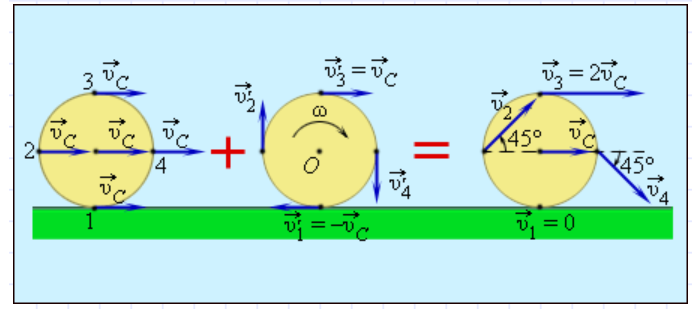
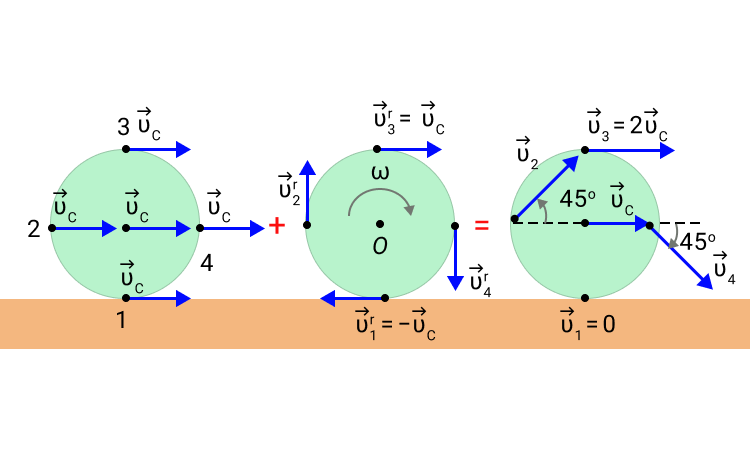
Можно сказать, что общее движение предмета включает поступательное и вращательное. Пример – качение чего-то округлого (рис. 4). При этом все перемещение точек можно исчерпывающе изобразить на рисунке. В таком варианте движение называется плоским.
Полная кинетическая энергия равна:
IC – момент инерции относительно оси, включающей центр масс.
Рис. 4 Качение колеса
Частные случаи вращательного движения
1. Равномерное (рис. 5), с постоянной скоростью, с нулевым ускорением.
Выражается уравнением: φ = φ0 + ωt
2. Равноускоренное. Рассмотрено ранее. Но все же уместны некоторые пояснения (рис. 6).
3. Вокруг неподвижной оси. Наиболее распространенный в рассмотрении вариант. Как для реальных нужд, так и в теории.
4. Возвратно-вращательное. В математическом выражении напоминает колебания. При подробном рассмотрении вызывает неудобные вопросы.
Заключение
Для разработчиков оборудования тема отнюдь не праздная. Рассматриваются задачи по передаче силового момента (в частности в ременных механизмах). Разбирается механика работы подшипников, гироскопов.
В артиллерии снаряды стабилизируются вращением. Да и расчеты их на прочность связаны со сложным напряженным состоянием в связи с раскручиванием в стволе.
Орбиты планет имеют отношение к рассматриваемой кинематике.
На самом деле все сферы использования данной темы невозможно перечислить, это действительно нужный раздел.
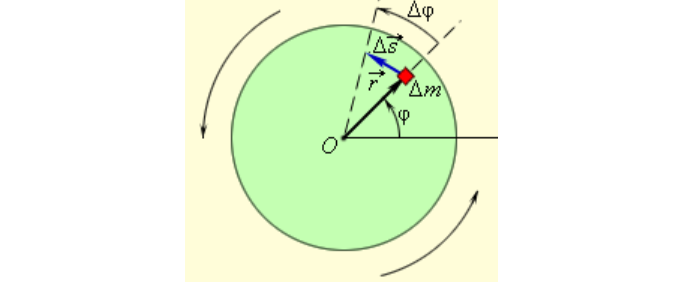
Вращение твердого тела
Углы выражаются в радианах. За положительное направление вращения принимается направление против часовой стрелки.
Когда твердое тело вращается относительно неподвижной оси, все точки этого тела перемещаются с одинаковыми угловыми скоростями и ускорениями.
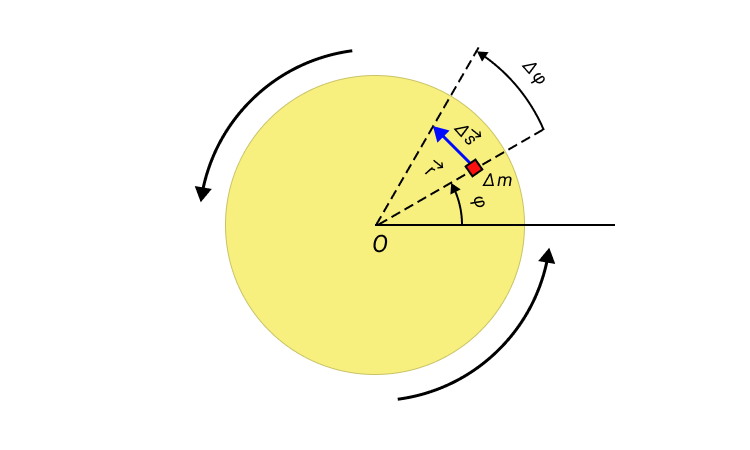
Если угловое перемещение Δ φ мало, то модуль вектора линейного перемещения ∆ s → некоторого элемента массы Δ m вращающегося твердого тела можно выразить соотношением:
Между модулями угловой и линейной скоростей можно установить связь посредством равенства
Модули линейного и углового ускорения также взаимосвязаны:
Также нам необходимо учесть возникновение нормального или центростремительного ускорения, которое всегда возникает при движении тел по окружности.
Модуль ускорения выражается формулой:
Физическая величина ∑ i ∆ m i r i 2 носит название момента инерции I тела относительно оси вращения. Она зависит от распределения масс вращающегося тела относительно оси вращения:
Если для динамики поступательного движения основную роль играет масса тела, то в динамике вращательного движения имеет значение момент инерции. Но если масса – это свойство рассматриваемого твердого тела, которое не зависит от скорости движения и других факторов, то момент инерции зависит от того, вокруг какой оси вращается тело. Для одного и того же тела момент инерции будет определяться различными осями вращения.
В большинстве задач считается, что ось вращения твердого тела проходит через центр его массы.
Рисунок 2. Центр масс C системы из двух частиц.
В векторной форме это соотношение принимает вид:
Аналогично, для системы из многих частиц радиус-вектор r C → центра масс определяется выражением
Если мы имеем дело с твердым телом, состоящим из одной части, то в приведенном выражении суммы для r C → необходимо заменить интегралами.
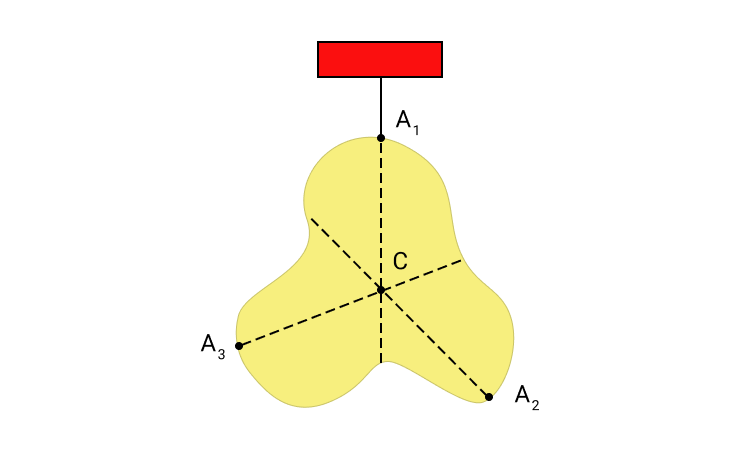
Центр масс в однородном поле тяготения совпадает с центром тяжести. Это значит, что если мы возьмем тело сложной формы и подвесим его за центр масс, то в однородном поле тяготения это тело будет находиться в равновесии. Отсюда следует способ определения центра масс сложного тела на практике: его необходимо последовательно подвесить за несколько точек, одновременно отмечая по отвесу вертикальные линии.
На рисунке мы видим тело, которое подвешено за центр масс. Оно находится в состоянии безразличного равновесия. В однородном поле тяготения равнодействующая сил тяжести приложена к центру масс.
Мы можем представить любое движение твердого тела как сумму двух движений. Первое поступательное, которое производится со скоростью центра масс тела. Второе – это вращение относительно оси, которая проходит через центр масс.
Предположим. Что у нас есть колесо, которое катится по горизонтальной поверхности без проскальзывания. Все точки колеса во время движения перемещаются параллельно одной плоскости. Такое движение мы можем обозначить как плоское.
Теорема о движении центра масс
Кинестетическая энергия вращающегося твердого тела при плоском движении будет равна сумме кинетической энергии поступательного движения и кинетической энергии вращения относительно оси, которая проведена через центр масс и располагается перпендикулярно плоскостям, в которых движутся все точки тела:
где m – полная масса тела, I C – момент инерции тела относительно оси, проходящей через центр масс.
В механике используется теорема о движении центра масс.
Любое тело или несколько взаимодействующих тел, которые представляют собой единую систему, обладают центром масс. Этот центр масс под воздействием внешних сил перемещается в пространстве как материальная точка, в которой сосредоточена вся масса системы.
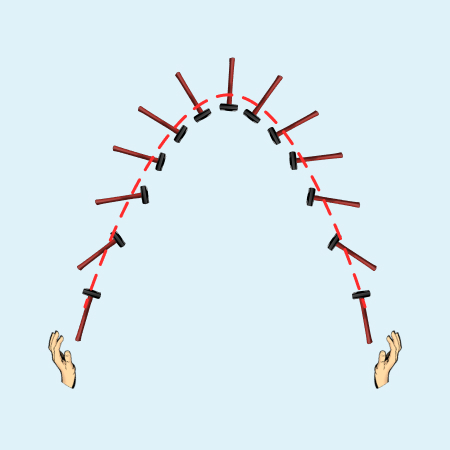
На рисунке мы изобразили движение твердого тела, на которое действуют силы тяжести. Центр масс тела движется по траектории, которая близка к параболе, тогда как траектория остальных точек тела является более сложной.
Рисунок 5. Движение твердого тела под действием силы тяжести.
Теорема Штейнера о параллельном переносе оси вращения
Рассмотрим случай, когда твердое тело движется вокруг некоторой неподвижной оси. Момент инерции этого тела инерции I можно выразить через момент инерции I C этого тела относительно оси, проходящей через центр масс тела и параллельной первой.
Рисунок 6. К доказательству теоремы о параллельном переносе оси вращения.
По определению момента инерции:
Выражение для I P можно переписать в виде:
Два последних члена уравнения обращаются в нуль, так как начало координат в нашем случае совпадает с центром масс тела.
Так мы пришли к формуле теоремы Штейнера о параллельном переносе оси вращения.
Для тела, которое вращается относительно произвольной неподвижной оси, момент инерции, согласно теореме Штейнера, равен сумме момента инерции этого тела относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями.
где m – полная масса тела.
Рисунок 7. Модель момента инерции.
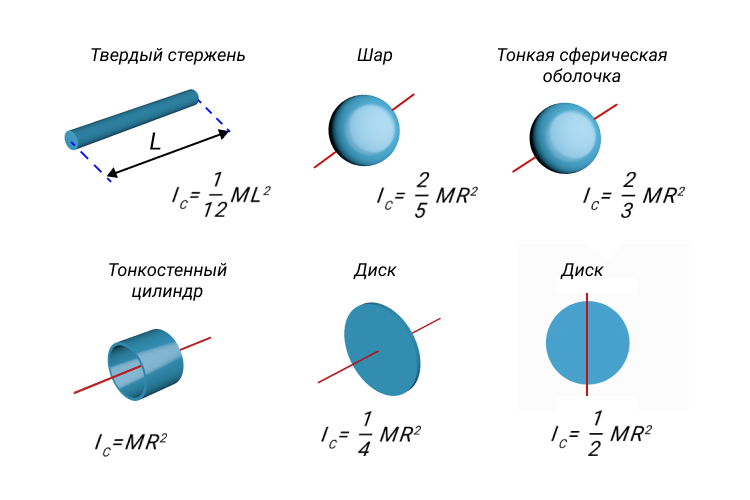
На рисунке ниже изображены однородные твердые тела различной формы и указаны моменты инерции этих тел относительно оси, проходящей через центр масс.
Рисунок 8. Моменты инерции I C некоторых однородных твердых тел.
Основное уравнение динамики вращательного движения твердого тела
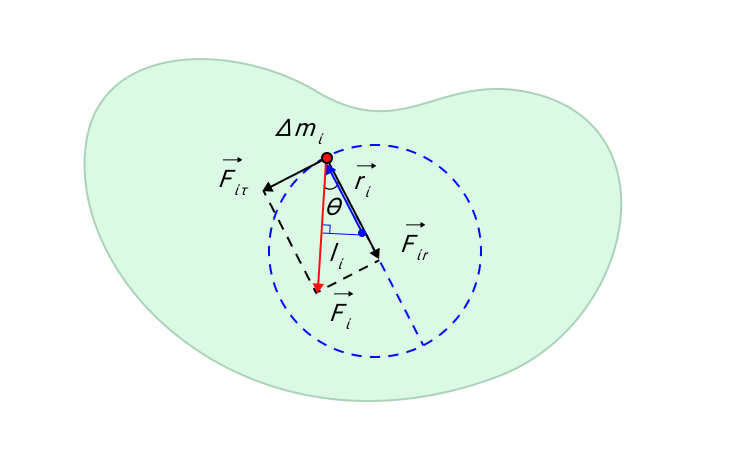
Рисунок 9. Касательная F i τ → и радиальная F i r → составляющие силы F i → действующей на элемент Δ m i твердого тела.
где ε = a i τ r i – угловое ускорение всех точек твердого тела.
Теперь нужно аналогичные соотношения записать для всех элементов массы Δmi вращающегося твердого тела, а затем просуммировать левые и правые части. Это дает:
Стоящая в правой части сумма моментов сил, действующих на различные точки твердого тела, состоит из суммы моментов всех внешних сил и суммы моментов всех внутренних сил.
Угловое ускорение ε и момент сил M в этом уравнении являются величинами алгебраическими.
Обычно за положительное направление вращения принимают направление против часовой стрелки.
Закон сохранения момента импульса
Момент импульса вращающегося тела – это физическая величина, которая равняется произведению момента инерции тела I на угловую скорость ω его вращения.
Так мы пришли к закону сохранения момента импульса.
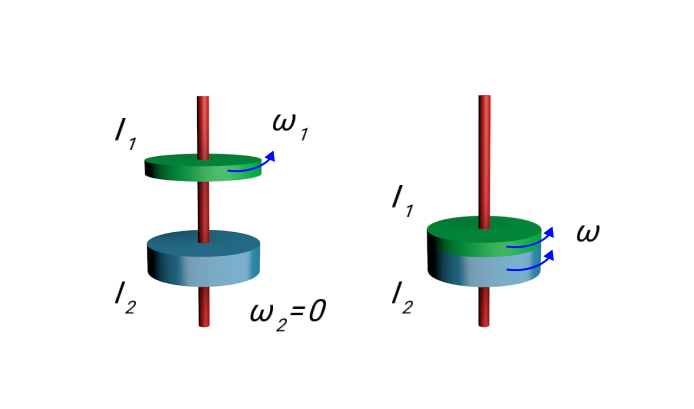
В качестве примера приведем рисунок, на котором изображено неупругое вращательное столкновение дисков, которые насажены на общую для них ось.
Мы имеем дело с замкнутой системой. Для любой замкнутой системы закон сохранения момента импульса будет справедливым. Он выполняется и в условиях экспериментов по механике, и в условиях космоса, когда планеты движутся по своим орбитам вокруг звезды.
Мы можем записать уравнение динамики вращательного движения как для неподвижной оси, так и для оси, которая перемещается равномерно или с ускорением. Вид уравнения не изменится и в том случае, если ось движется ускоренно. Для этого должно выполняться два условия: ось должна проходить через центр массы тела, а ее направление в пространстве остается неизменным.
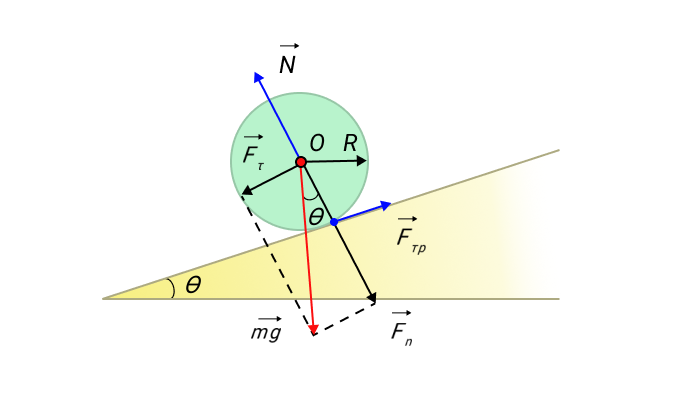
Предположим, что у нас есть тело (шар или цилиндр), которое катится по наклонной плоскости с некоторым трением.
Рисунок 11. Качение симметричного тела по наклонной плоскости.
Уравнение вращательного движения:
Второй закон Ньютона для поступательного движения центра масс записывается в виде: