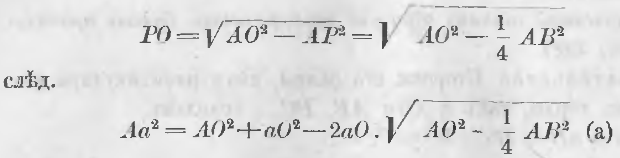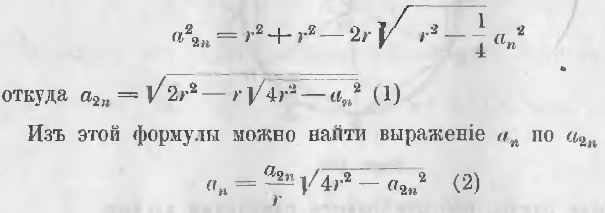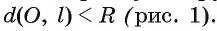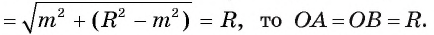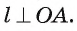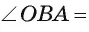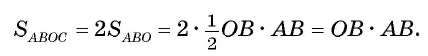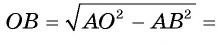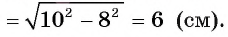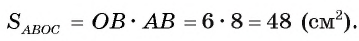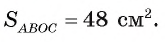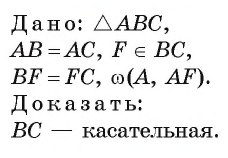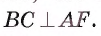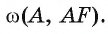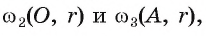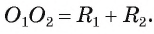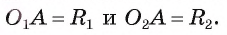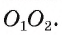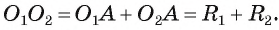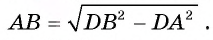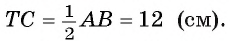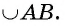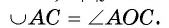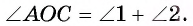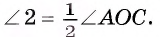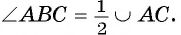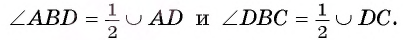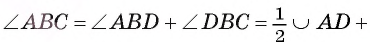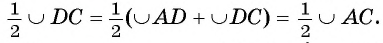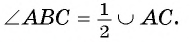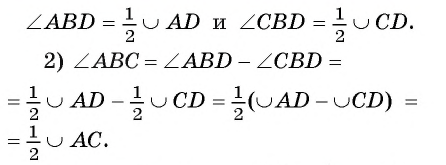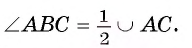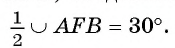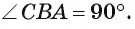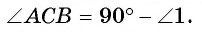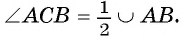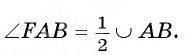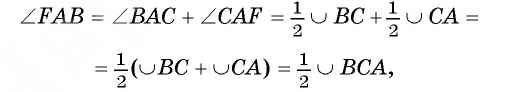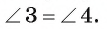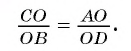что такое вписанные многоугольники

Математика

Правильный многоугольник. Правильным называется такой многоугольник, у которого все стороны и все углы равны.

Правильный треугольник есть равносторонний треугольник, каждый угол которого равен (2/3)d или 60°.

Правильный четырехугольник есть квадрат, каждый угол которого равен прямому углу или 90°.

Правильный многоугольник, имеющий n сторон, есть многоугольник, каждый угол которого равен .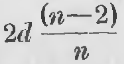

Таким образом, полагая n = 3, 4, 5, 6, мы имеем для каждого угла величину (2/3)d, d, (6/5)d, (4/3)d и т. д.

Угол правильного пятиугольника равен (6/5)d = 108°, угол правильного шестиугольника равен (4/3)d = 120° и т. д.

Одноименные многоугольники. Все многоугольники, имеющие одинаковое число углов, называются одноименными многоугольниками.

Все правильные одноименные многоугольники имеют одинаковые углы и различаются только величиной сторон.

Подобие правильных многоугольников. Одноименные правильные многоугольники подобны, ибо у них углы равны и стороны пропорциональны.

Из подобия их вытекает, что периметры одноименных правильных многоугольников относятся как стороны.

Теорема 117. Около правильного многоугольника всегда можно описать окружность.

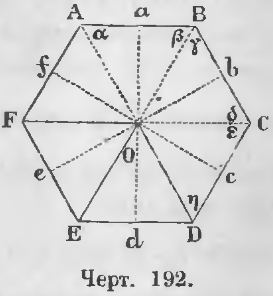
Дан правильный многоугольник ABCDEF (черт. 192). Стороны его и углы равны между собой:

AB = BC = CD = DE = EF = AF и
A = B = C = D = E = F

Требуется доказать, что существует точка, равноотстоящая от всех его вершин.

Доказательство. Проведем через три точки A, B, C окружность. Для этого из середины линий AB и BC восставляем перпендикуляры до взаимного их пересечения в точке O. Точка O есть центр круга, проходящего через три точки A, B, C. Докажем, что эта окружность пройдет и через точки D, E, F. Для этого соединим точку O с вершинами многоугольника отрезками AO, BO, CO, DO, EO, FO.

1. Все эти отрезки разделяют углы многоугольника пополам.

Из равнобедренных треугольников AOB и BOC видно, что

Так как ΔABO = ΔBCO, то

т. е. угол B делится пополам.

следует, что угол C тоже делится пополам.

Точно также легко доказать, что угол D тоже делится пополам.

Треугольники BOC и COD равны, ибо OC сторона общая, BC = CD как стороны правильного многоугольника, ∠δ = ∠ε, следовательно, ∠γ = ∠η.

Так как ∠γ = ½B = ½C = ½D, то и угол η = ½D, т. е. угол D делится тоже пополам.

Подобным образом легко доказать, что все углы многоугольника делятся пополам отрезками, соединяющими точку O с вершинами многоугольника.

2. Все отрезки OA, OB, OC, OD, OE, OF равны.

Действительно, по построению следует, что

Из равенства треугольников BOC и COD следует, что

Из равенства треугольников COD и DOE следует, что

Таким образом точка O находится на равном расстоянии от всех вершин многоугольника, т. е. окружность, описанная радиусом OA, пройдет через все вершины многоугольника, и точка O будет центром описанного многоугольника (ЧТД).

Теорема 118. Центр описанного круга будет также центром круга, вписанного в правильный многоугольник.

Доказательство. Из точки O центра описанного многоугольника (черт. 192) опустим перпендикуляры Oa, Ob, Oc, Od, Oe, Of на стороны многоугольника. Так как треугольники ABO, BCO равнобедренные и многоугольники правильные, то

Два прямоугольных треугольника aBO и BbO равны, ибо BO сторона общая

следовательно, Oa = Ob.

Точно также легко доказать, что Ob = Oc и т. д.

Следовательно, вообще Oa = Ob = Oc = Od = Oe = Of.

Если мы радиусом Oa опишем окружность, то она коснется сторон правильного многоугольника в точках a, b, c, … т. е. она будет вписана в многоугольник.

Точки a, b, c, … делят стороны многоугольника пополам.

Таким образом точка O, будучи центром описанного, есть в то же время и центр круга, вписанного в правильный многоугольник (ЧТД).

Апофема. Перпендикуляр, опущенный из центра на сторону правильного многоугольника, называется апофемой.

Теорема 119. Периметры одноименных правильных многоугольников относятся как радиусы описанных и вписанных кругов.

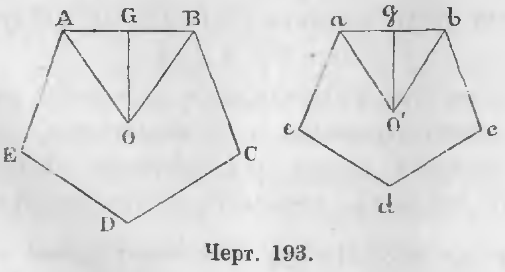
Даны два правильных одноименных многоугольника (черт. 193). Из центров O и O’ проведем радиусы кругов описанных и вписанных.

Требуется доказать, что

(AB + BC + CD + DE + EA) / (ab + bc + cd + de + ea) = OA/O’a = OG/O’g

Доказательство. Два треугольника GOB и gOb подобны, ибо они прямоугольны и ∠GBO = ∠gbO’, следовательно,

Так как GB = ½AB, gb = ½ab, то

AB/ab = OB/O’b = GO/gO’ (a)

Кроме того имеют место следующие равенства отношений:

AB/ab = BC/bc = CD/cd = DE/de = EA/ea

откуда по свойству пропорций имеем:

(AB + BC + CD + DE + EA) / (ab + bc + cd + de + ea) = AB/ab

Обозначим периметры этих многоугольников через P и p, имеем:

Сравнивая пропорции (a) и (b), получаем равные отношения:

P/p = AB/ab = OB/O’b = GO/gO’ (ЧТД).

Теорема 120. Если углы описанного многоугольника равны, то и стороны равны, т. е. равноугольный описанный есть многоугольник правильный.

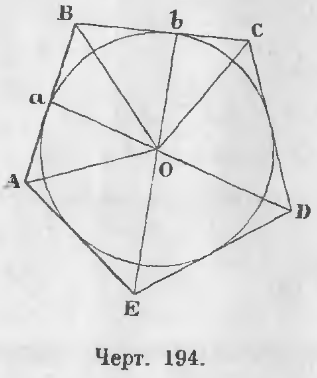
Дано. В описанном многоугольнике ABCDE углы равны (черт. 194):

Требуется доказать, что AB = BC = CD = DE = EA.

Доказательство. Соединим вершины описанного многоугольника и точки прикосновения с центром круга O.

1. Два прямоугольных треугольника aBO и BbO равны, ибо у них BO сторона общая, aO = bO как радиусы, следовательно, ∠aOB = ∠Bob и ∠aBO = ∠bBO, т. е. отрезки, соединяющие вершины описанного многоугольника с центром, делят углы многоугольника пополам.

2. Треугольники AOB и BOC равны, ибо BO сторона общая, ∠ABO = ∠CBO по доказанному, ∠BAO = ∠BCO по условию, следовательно, AB = BC.

Таким образом можно доказать равенство остальных сторон описанного многоугольника, имеющего равные углы (ЧТД).

Теорема 121. По данному вписанному правильному многоугольнику можно описать правильный многоугольник того же числа сторон.

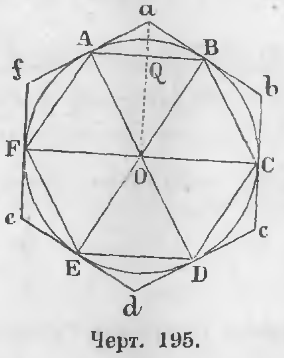
Дан правильный вписанный многоугольник (черт. 195) ABCDEF, следовательно, стороны и углы его равны.

AB = BC = CD = DE = EF = FA и
◡AB = ◡BC = ◡CD = ◡DE = ◡EF = ◡FA

Для построения правильного описанного многоугольника по данному вписанному применяют два способа.

Первый способ. Нужно центр правильного вписанного многоугольника соединить с вершинами и в вершинах провести к этим отрезкам перпендикуляры, которые, пересекаясь, образуют правильный описанный многоугольник.

Проведем радиусы AO, BO, CO, и т. д. и в вершинах A, B, C, D, E, F проведем перпендикуляры к этим радиусам до взаимного их пересечения в точках a, b, c, d, e, f. Образуется многоугольник abcdef.

Требуется доказать, что многоугольник abcdef будет правильным описанным многоугольником.

Доказательство. Многоугольник abcdef будет описанным многоугольником, потому что ab, bc, … будут касательными к окружности, так как они проведены перпендикулярно к радиусам из их концов.

2. Треугольники AaB, BbC … равнобедренны, ибо

∠aAB = ∠aBA
∠bBC = ∠bCB и т. д.

так как они измеряются половиной одной и той же дуги, следовательно, и соответствующие стороны равны

aA = aB, bB = bC, cC = Dc и т. д.

3. Треугольники AaB и BbC равны, ибо AB = BC как стороны правильного вписанного многоугольника

ибо они измеряются половиной равных дуг.

Из равенства треугольников AaB и BbC вытекает, что aB = Bb, т. е.

Каждая сторона таким образом описанного многоугольника делится в точке прикосновения пополам.

aA = aB, или ½af = ½ab = ½bc и т. д.

af = ab = bc = cd и т. д.,

т. е. все стороны многоугольника равны.

5. Наконец, ∠a = ∠b, следовательно и все углы многоугольника abcdef равны. Поэтому этот многоугольник правильный (ЧТД).

Второй способ. Нужно из центра на стороне правильного вписанного многоугольника опустить перпендикуляры, продолжить их до пересечения с окружностью и в точках пересечения провести касательные прямые до взаимного их пересечения. Эти точки пересечения и будут вершинами правильного описанного многоугольника.

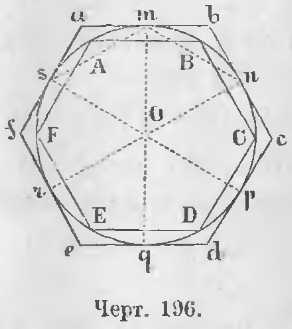
Дан правильный вписанный многоугольник ABCDEF (черт. 196).

Из центра O опустим перпендикуляр на стороны вписанного многоугольника и в точках m, n, p, q, r, s их встречи с окружностью проведем касательные до их взаимного пересечения в точках a, b, c, d, e, f.

Требуется доказать, что abcdef есть правильный описанный многоугольник.

Доказательство. 1. Стороны многоугольника abcdef касательны к окружности, следовательно, abcdef есть многоугольник описанный.

2. Его стороны параллельны сторонам правильного вписанного многоугольника, поэтому его углы равны

3. Соединим точки m, n, p, q … прямыми линиями.

Точки m, n, p, q … суть середины дуг AB, BC и т. д., следовательно, для дуг и хорд имеют место равенства:

sm = mn = np = pq = qr = rs.

4. Треугольники sam, mbn, ncp … равнобедренны, ибо

∠asm = ∠ams, ∠bmn = ∠bnm и т. д.

as = am, bm = bn, cn = cp и т. д.

5. Треугольники sam и mbn равны, ибо

следовательно, am = bm, т. е. стороны описанного многоугольника делятся в точках прикосновения пополам.

6. Наконец из равенства as = am следует равенство

½af = ½ab или af = ab, т. е.

стороны описанного многоугольника равны.

Таким образом многоугольник abcdef есть правильный описанный многоугольник (ЧТД).

Теорема 122. По данному правильному описанному можно вписать правильный многоугольник того же числа сторон.

Здесь тоже имеют место два способа.

Первый способ. Чтобы по данному правильному описанному вписать правильный многоугольник, нужно соединить точки прикосновения описанного многоугольника между собой.

Дан описанный правильный многоугольник abcdef, следовательно,

ab = bc = cd = de = ef = fa и
∠a = ∠b = ∠c = ∠d = ∠e = ∠f.

Стороны правильного описанного многоугольника (черт. 195) делятся в точках прикосновения пополам, следовательно,

Соединим точки прикосновения A, B, C, D, E, F между собой.

Требуется доказать, что ABCDEF есть правильный вписанный многоугольник, т. е.

AB = BC = CD = DE = EF = FA и
∠A = ∠B = ∠C = ∠D = ∠E = ∠F.

Доказательство. 1. Треугольники AaB и BbC равны, ибо они имеют по равному углу, содержащемуся между двумя равными сторонами. Действительно,

aA = bC
aB = bB
∠a = ∠b

следовательно, AB = BC.

Точно также можно доказать, что

BC = CD = DE = EF = FA,

следовательно, и стороны и дуги AB, BC, CD … равны.

Таким образом стороны вписанного многоугольника равны.

Подобным же образом можно доказать равенство других углов, следовательно,

Таким образом углы вписанного многоугольника как и стороны тоже равны, следовательно, ABCDEF правильный вписанный многоугольник (ЧТД).

Второй способ. Чтобы по данному правильному описанному многоугольнику вписать правильный одноименный многоугольник, соединим его вершины с центром круга и точки пересечения этих отрезков с окружностью соединим между собой.

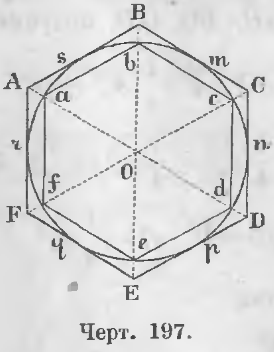
Дан правильный описанный многоугольник ABCDEFA (черт. 197), следовательно,

AB = BC = CD = DE = EF = FA
∠A = ∠B = ∠C = ∠D = ∠E = ∠F

и стороны его делятся в точках прикосновения пополам, т. е.

As = Bs = Cm = Cn = Dn = и т. д.

Соединим вершины его с центром и означим точки пересечения этих линий с окружностью через a, b, c, d, e, f.

Требуется доказать, что многоугольник abcdef правильный.

Доказательство. 1. Углы при центре AOB, BOC, COD и т. д. равны, а следовательно и дуги ab, bc, de, ef, fa равны.

Отсюда вытекает, что стороны тоже равны

ab = bc = cd = de = ef = fa

2. Углы многоугольника тоже равны, ибо измеряются дугами одинаковой величины.

Теорема 123. По данной стороне правильного вписанного многоугольника можно определить сторону описанного многоугольника того же числа сторон.

Означим длину стороны вписанного правильного многоугольника имеющего n сторон через a_n и одноименного описанного многоугольника через A_n, а радиус круга через r (черт. 195)

AB = BC = CD = DE = … = a_n
ab = bc = cd = de = … A_n

Соединим точку a с O, тогда

Из треугольника aBO имеем:

формулу, определяющую сторону правильного вписанного многоугольника по стороне одноименного правильного описанного многоугольника.

Удвоение числа сторон правильного вписанного многоугольника

Чтобы удвоить число сторон правильного вписанного многоугольника, опускают из центра перпендикуляры на его стороны, соединяют с вершинами данного многоугольника точки пересечения их с окружностью.

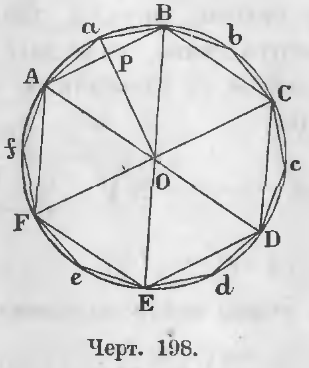
1. Полученный таким образом многоугольник будет правильным (черт. 198).

Доказательство. Стороны его равны, ибо перпендикуляры делят как хорды, так и дуги AB, BC, … пополам, следовательно,

Aa = aB = Bb = bC = Cc = …

Углы тогда равны, ибо измеряются одинаковыми дугами.

2. Периметр многоугольника при удвоении числа сторон увеличивается.

Aa + aB > AB
Bb + bC > BC и т. д.

Складывая эти неравенства, получим

Обозначив периметр правильного многоугольника, имеющего n сторон, через p_n, имеем:

Теорема 124. Можно определить длину стороны вписанного многоугольника с удвоенным числом сторон по радиусу и стороне данного многоугольника.

Из треугольника AaO (черт. 198) длина стороны Aa, как стороны, лежащей против острого угла, выражается равенством:

Из треугольника APO имеем:

Обозначив через r радиус круга, a_n длину стороны правильного вписанного многоугольника, имеющего n сторон, и через a_2n сторону многоугольника с удвоенным числом сторон, мы имеем по формуле (a)

Удвоение числа сторон правильного описанного многоугольника

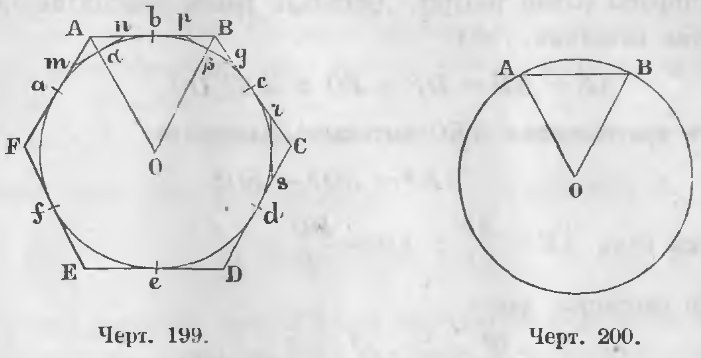
Чтобы удвоить число сторон правильного описанного многоугольника нужно разделить дуги ab, bc, cd, … пополам и провести через точки деления отрезки mn, pg, rs, … до пересечения их со сторонами данного многоугольника (черт. 199).

В этом случае образуется многоугольник равноугольный, ибо его углы измеряются одинаковой мерой. В равноугольном же описанном многоугольнике стороны равны (теорема 120).

Периметр описанного многоугольника с удвоенным числом сторон уменьшается.

An > α n
Bp > β p, следовательно,
AB > α n + np + p β

Такие же равенства имеют место и для сторон BC, CD, … и т. д. Сложив их, находим, что

AB + BC + CD + … > mn + np + pq + …
или P_n > P_2n

где P_n и P_2n означают периметры правильных описанных многоугольников, имеющих n и 2n сторон.

Теорема 125. Сторона правильного вписанного шестиугольника равна радиусу (a₆ = r).

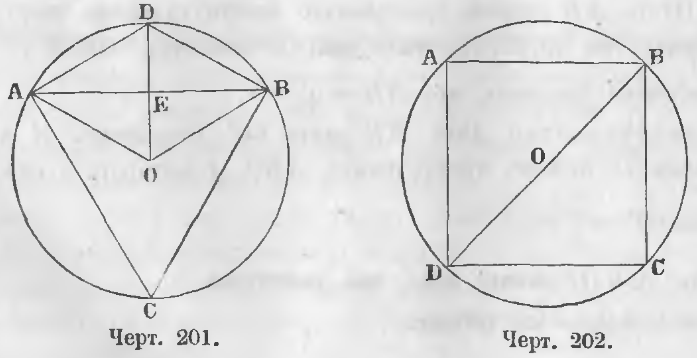
Дано. Пусть AB сторона правильного шестиугольника (черт. 200), вписанного в круг, радиус которого обозначим через r.

Требуется доказать, что AB = a₆ = r.

Доказательство. Дуга AB равна 60°. Соединив A и B с центром O, имеем треугольник ABO, у которого угол AOB имеет 60° = (2/3)d.

Углы A и B равны, следовательно, из равенства A + B + O = 2d, имеем:

2A + (2/3)d = 2d, откуда A = B = (2/3)d

Таким образом треугольник ABO равносторонний и следовательно AB = AO = r.

Теорема 126. Сторона правильного вписанного треугольника равна радиусу, умноженному на √3 (a₃ = r√3).

Дан правильный вписанный треугольник ABC (черт. 201).

Требуется доказать, что AB = r√3.

Доказательство. Из центра O опустим перпендикуляр OD к стороне AB и соединим D с вершинами A и B. Стороны AD и DB как стороны правильного вписанного шестиугольника равны радиусу. Четырехугольник ADBO есть ромб, ибо у него все стороны равны радиусу. Диагонали ромба перпендикулярны и делятся пополам, следовательно,

AE = EB = DE = EO и AB ⊥ DO.

Из треугольника AEO вытекает равенство

Так как AE = AB/2, EO = DO/2 = r/2, то это равенство дает

Теорема 127. Сторона вписанного квадрата равна радиусу, умноженному на √2.

Дан правильный вписанный четырехугольник или квадрат ABCD (черт. 202).

Требуется доказать, что AB = r√2.

Доказательство. Соединим B с D. Отрезок BD есть диаметр, ибо прямой угол B опирается на концы диаметра.

Из прямоугольного треугольника ABD вытекает равенство

Так как AB = AD, BD = 2r, то

Теорема 128. Сторона правильного вписанного десятиугольника равна большей части радиуса, разделенного в крайнем и среднем отношении.

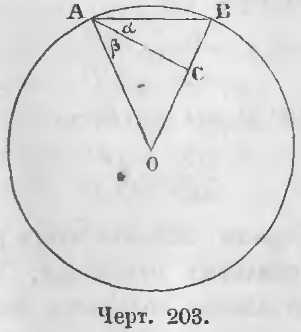
Дано. Положим AB есть сторона правильного вписанного десятиугольника (черт. 203), следовательно, дуга AB = 1/10 окружности и

Требуется доказать, что AB есть большая часть радиуса среднепропорциональная между целым радиусом и меньшей его частью.

Доказательство. Соединим точки A и B с центром и разделим угол BAO пополам.

В равенстве ∠BAO + ∠ABO + ∠AOB = 2d

∠BAO = ∠ABO, следовательно, ∠BAO = ∠ABO = (4/5)d.

Так как ∠α = ∠β по построению, то из равенства

∠α + ∠β = (4/5)d следует, что ∠α = ∠β = (2/5)d

Треугольник ABC равнобедренный, ибо

следовательно, из равенства

∠α + ∠B + ∠ACB = 2d имеем:
(2/5)d + (4/5)d + ∠ACB = 2d и ∠ACB = (4/5)d.

Треугольник ACO тоже равнобедренный, ибо

следовательно, AC = CO и таким образом AB = AC = CO.

Так как отрезок AC делит угол треугольника пополам, то имеет место пропорция (теорема 98)

Так как AB = OC и AO = OB, то

откуда видно, что OC равно большей части радиуса OB, разделенного в крайнем и среднем отношении. Так как OC = AB, то и сторона десятиугольника обладает тем же свойством.

Обозначив ее через a₁₀, а радиус через r, имеем пропорцию

откуда положительное решение квадратного уравнения, определяющее сторону правильного вписанного десятиугольника, будет:

Источник

Содержание:

Рассмотрим вопрос о взаимном расположении прямой и окружности. Ранее уже отмечалось, что возможны три случая взаимного расположения прямой и окружности:

Если прямая имеет две общие точки с окружностью, то она называется секущей.

Понятие о вписанных и описанных многоугольниках

Взаимное расположение окружности со (О, R) с центром в точке О радиуса R и прямой I характеризуется соотношением между расстоянием d(0, I) от центра О окружности до прямой I и радиусом R окружности. Докажем это.

1) Прямая I имеет только две общие точки с окружностью, если расстояние от центра окружности до прямой I меньше радиуса окружности, т. е.

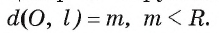
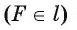
Пусть прямая I не проходит через центр О окружности и расстояние . Обозначим OF — перпендикуляр, проведенный из точки О к прямой I, тогда OF = m. Пусть точки А и В лежат на прямой I

так, что 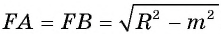. Докажем, что точки А и В принадлежат окружности.

Действительно, так как по теореме Пифагора

Таким образом, точки А и В — общие точки прямой и окружности. Докажем, что других общих точек прямая I и окружность 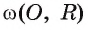не имеют.

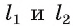
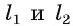
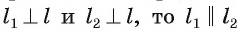
Предположим, что существует еще одна точка X — общая для окружности и прямой. Тогда центр окружности О равноудален от точек А, В, и X, а значит, он лежит на серединных перпендикулярах к отрезкам АВ и ВХ, т. е. О — точка перессечения серединных перпендикуляров. Но так как,. Получили противоречие. Значит, наше предположение не верно и других общих точек прямой и окружности нет.

Если прямая I проходит через центр О окружности, т. е. d(0, Z) = 0, то она пересекает окружность в двух точках, которые являются концами диаметра, лежащего на этой прямой.

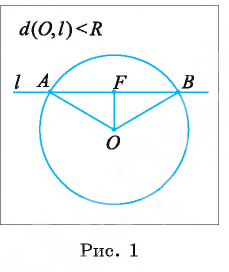
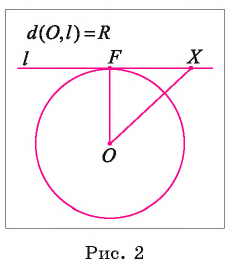
2) Прямая I имеет только одну общую точку с окружностью, если расстояние от центра окружности до прямой I равно радиусу окружности, т. е. если d(0, I) = R.

Пусть расстояние от центра окружности до прямой I равно радиусу окружности, а точка F — основание перпендикуляра, проведенного из центра окружности к прямой I (рис. 2). Тогда OF = R, а значит, точка F лежит на окружности. Других общих точек прямая и окружность не имеют. Действительно, для любой точки X прямой I, не совпадающей с точкой F, выполняется условие ОХ > OF, OF = R, так; как наклонная ОХ больше перпендикуляра OF.

Следовательно, точка X не лежит на окружности.

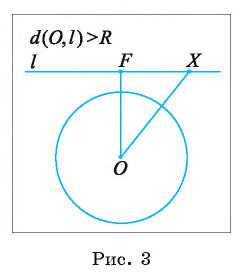
3) Прямая I не имеет общих точек с окружностью, если расстояние от центра О окружности до прямой I больше радиуса окружности, т. е. если d(0, I) > R.

Пусть расстояние от центра О окружности до прямой I больше радиуса R. Обозначим буквой F основание перпендикуляра, проведенного из центра О окружности к прямой I (рис. 3). Тогда OF = d(0, I), d(0, I) > R.

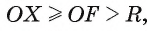
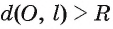
Для любой точки X прямой выполняется условие , следовательно, точка X не лежит на окружности. Таким образом, в случае прямая и окружность не имеют общих точек.

Касательная к окружности

Рассмотрим случай, когда прямая и окружность имеют единственную общую точку. Прямая, имеющая единственную общую точку с окружностью, имеет специальное название — касательная.

Определение. Касательной к окружности называется прямая, которая имеет с окружностью только одну общую точку.

Единственная общая точка прямой и окружности называется точкой касания прямой и окружности.

Если прямая I имеет единственную общую точку А с окружностью, то говорят, что прямая I касается окружности в точке А.

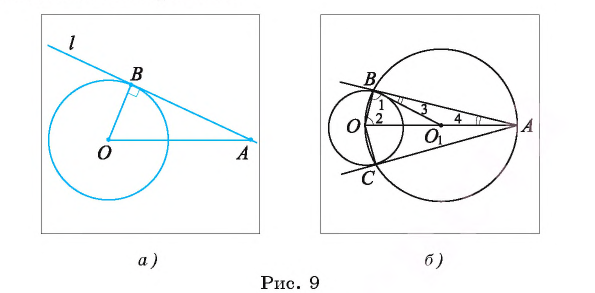
Теорема 1 (о свойстве касательной). Касательная к окружности перпендикулярна радиусу этой окружности, проведенному в точку касания.

1) Пусть прямая I касается окружности 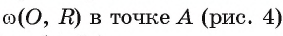Докажем, что

2) Предположим, что это не так. Тогда радиус ОА является наклонной к прямой I. Перпендикуляр, проведенный из точки О к прямой I, меньше наклонной ОА, следовательно, расстояние от центра окружности до прямой

меньше радиуса. Значит, прямая и окружность имеют две общие точки, что противоречит условию. Таким образом, прямая I перпендикулярна радиусу ОА.

Рассмотрим следствия из данной теоремы.

Пусть через точку А проведены две прямые, касающиеся окружности 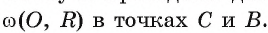Тогда отрезки АВ и АС называются отрезками касательных, проведенными из точки А (рис. 5).

Следствие 1. Отрезки касательных к окружности, проведенные из одной точки, равны.

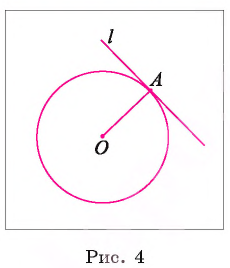
1) Пусть АВ и АС — отрезки касательных, проведенные из точки А (рис. 5). Для доказательства равенства АВ = АС рассмотрим треугольники АВО и АСО.

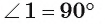
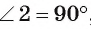
2) По свойству касательной и , т. е. треугольники АВО и АСО — прямоугольные.

3), так как АО — общая гипотенуза, а катеты О В и ОС равны как радиусы окружности. Отсюда следует, что АВ =АС.

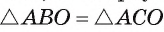
Следствие 1 доказано.

Из равенства треугольников АВО и АСО вытекает также, что 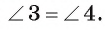. Таким образом, получим еще одно следствие.

Следствие 2. Отрезки касательных к окружности, проведенные из одной точки, составляют равные углы с прямой, проходящей через эту точку и центр окружности.

Теперь докажем признак, который позволяет устанавливать, в каком случае прямая касается окружности. Оказывается, для этого достаточно установить, что прямая перпендикулярна радиусу и проходит через его конец, лежащий на окружности.

Теорема 2 (признак касательной). Если прямая перпендикулярна радиусу окружности и проходит через его конец, лежащий на окружности, то она касается этой окружности.

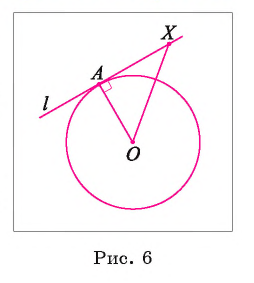
1) Пусть прямая I проходит через точку А окружности и перпендикулярна радиусу О А (рис. 6). Для доказательства того, что прямая I касается окружности, достаточно доказать, что она имеет с этой окружностью единственную общую точку.

2) Так как точка А лежит на окружности и прямая I проходит через точку А, то А — общая точка прямой I и окружности.

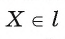
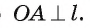
3) Других общих точек прямая I и окружность не имеют. Действительно, для любой точки отрезок ОХ является наклонной, так как по условию Следовательно, ОХ > ОА, т. е. точка X не принадлежит окружности.

Таким образом, точка А — единственная общая точка прямой I и окружности, а, значит, прямая I — касательная к окружности.

Пример №1

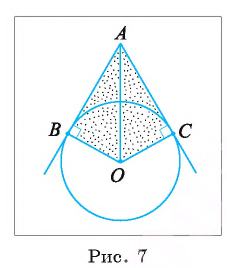
Через точку А, находящуюся от центра О окружности на расстоянии 10 см, проведены две касательные АВ и АС, где Б и С — точки касания. Вычислите площадь 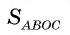четырехугольника АВОС, если АВ + АС = = 16 см ( рис. 7).

Решение:

1) Площадь четырехугольника АВОС равна сумме площадей треугольников АВО и АСО.

2) По свойству касательной 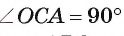. Прямоугольные треугольники АВО и АСО равны по гипотенузе и катету (АО — общая, ОВ = ОС). Значит,

3) Отрезки касательных к окружности, проведенные из одной точки, равны. Следовательно, АВ=АС = 8 см. Теперь, применив теорему Пифагора, вычислим

Таким образом,

Ответ:

Пример №2

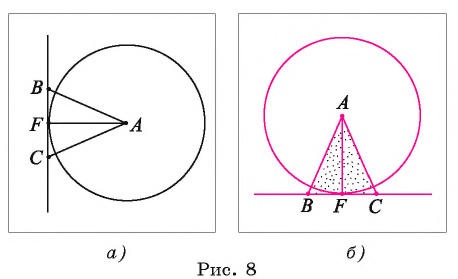
Точка F — середина основания ВС равнобедренного треугольника АБС. Докажите, что прямая ВС является касательной к окружности 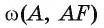(рис. 8, а, б).

Доказательство.

1) Прямая ВС проходит через конец F радиуса окружности 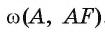. Для доказательства того, что ВС является касательной, достаточно доказать, что

2) В равнобедренном треугольнике AВС отрезок AF — медиана, проведенная к его основанию. Следовательно, 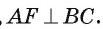Таким образом, по признаку касательной прямая ВС касается окружности

Что и требовалось доказать.

Пример №3

Точка А лежит вне окружности 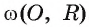Постройте прямую, которая касается окружности и проходит через точку А.

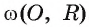
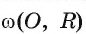
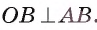
1) Пусть прямая I, проходящая через точку А и касающаяся окружности , построена. Точка В — точка касания. Тогда по свойству касательной OB LAB (рис. 9, а). Следовательно, для построения искомой касательной необходимо построить точку В на окружности так, что .

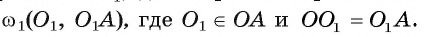
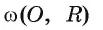
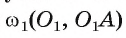
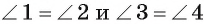
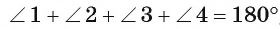
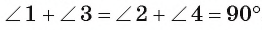
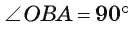
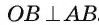
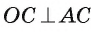
2) Рассмотрим окружность coj, диаметром которой является отрезок АО, т. е. Пусть В и С — точки пересечения окружностей и (рис. 9, б). Заметим, что , как углы при основании равнобедренных треугольников ВО,О и ВО,А соответственно. Так как , то Значит, , т. е.. Аналогично доказывается, что. Отсюда по признаку

касательной к окружности следует, что прямые АВ и АС являются касательными. Теперь понятна последовательность необходимых построений.

1) Проводим отрезок О А, соединяющий центр О данной окружности и точку А (рис. 10, а).

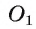
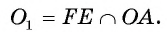
2) Строим середину отрезка ОА: Точки F и Е — точки пересечения окружностей

где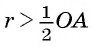(рис. 10, б).

3) Строим окружность 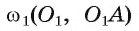(рис. 10, в) и точки Б, С — точки пересечения данной и построенной окружностей.

4) Прямые АВ и АС — искомые касательные к данной окружности.

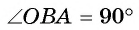
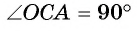
Доказательство. По построению и (см. задачу № 251 учебного пособия «Геометрия, 7»), т. е. АВ1ОВ и АС 1ОВ. Следовательно, по признаку касательной АВ и АС — касательные.

Взаимное расположение двух окружностей

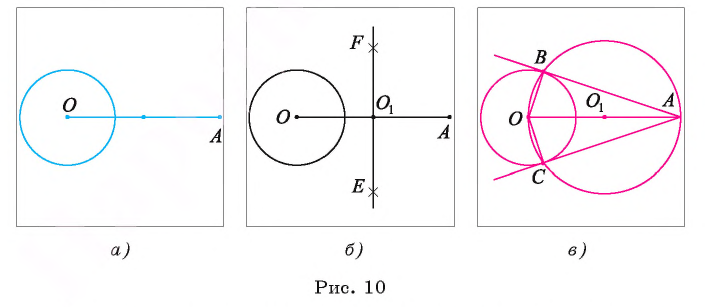
Рассмотрим вопрос о взаимном расположении двух окружностей в плоскости. Возможны следующие случаи взаимного расположения двух различных окружностей:

1) окружности не имеют общих точек (в этом случае говорят, что они не пересекаются (рис. 11, а ));

2) окружности имеют две общие точки (в этом случае говорят, что окружности пересекаются (рис. 11, б));

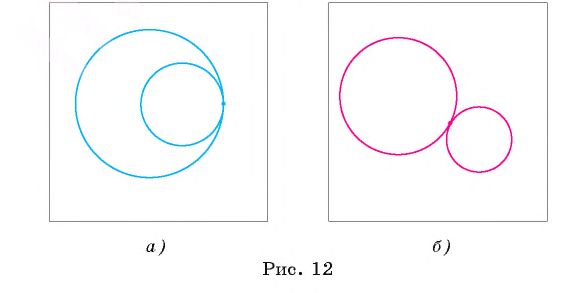
3) окружности имеют только одну общую точку, и одна из окружностей лежит внутри круга, ограниченного другой окружностью (в этом случае говорят, что они касаются внутренним образом (рис. 12, а ));

4) окружности имеют только одну общую точку, и ни одна из окружностей не лежит внутри круга, ограниченного другой окружностью (в этом случае говорят, что они касаются внешним образом, (рис. 12, б)).

Пример №4

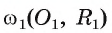
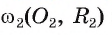
Докажите, что если две окружности и касаются внешним образом, то расстояние между их центрами равно сумме их радиусов, т. е.

Доказательство.

1) Пусть окружности 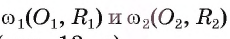касаются внешним образом в точке А (рис. 13, а).

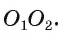
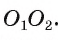
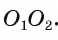
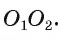
2) Докажем, что точка А лежит на отрезке Допустим, что точка А не лежит на отрезке Заметим, что в случае внешнего касания точка А не может лежать на продолжении отрезка Пусть точка касания А не лежит на отрезке (рис. 13, б). Тогда

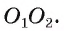
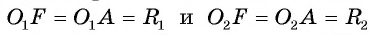
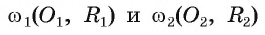
3) Пусть F — точка, симметричная точке А относительно прямой . Тогда , а значит, точка F принадлежит каждой окружности. Таким образом, окружности имеют две общие точки А и F, что противоречит условию их касания. Следовательно, точка касания А лежит на отрезке

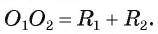
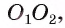
4) Докажем, что Точка А лежит на отрезке значит,

Справедливо и обратное утверждение.

Пример №5

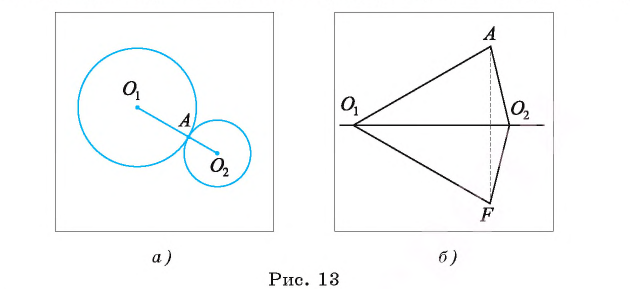
Докажите, если расстояние между центрами двух окружностей, лежащих в плоскости, равно сумме их радиусов, то такие окружности касаются внешним образом.

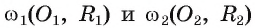
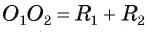
1) Пусть даны две окружности и известно, что Докажем, что окружности касаются внешним образом.

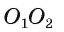
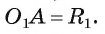
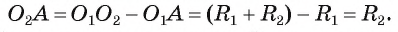
2) На отрезкерассмотрим точку А такую, что Тогда . Таким образом, точка А принадлежит каждой из данных окружностей.

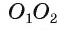
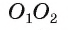
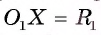
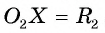
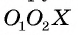
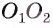
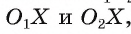
3) Докажем, что окружности не имеют других общих точек. Действительно, на прямой таких точек нет. Предположим, что существует точка X вне прямой принадлежащая каждой окружности. Тогда и В треугольнике длина стороныравна сумме длин сторон , что невозможно.

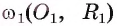
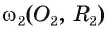
4) Таким образом, предположение о существовании еще одной точки, принадлежащей окружностям и , приводит к противоречию. Следовательно, других общих точек, кроме точки А, не существует, т. е. окружности касаются.

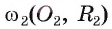
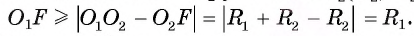
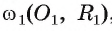
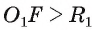
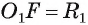
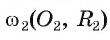
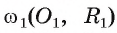
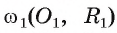
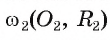
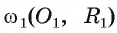
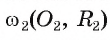
5) Докажем, что окружности касаются внешним образом. Для любой точки F окружностивыполняется условие Таким образом, либо точка F лежит вне окружности когда , либо эта точка принадлежит обеим окружностям, если Но в этом случае точка F есть точка А касания окружностей. Следовательно, окружность расположена вне части плоскости, ограниченной окружностью . Аналогично можно доказать, что окружность расположена вне части плоскости, ограниченной окружностью . Теперь доказано, что окружности и касаются внешним образом.

Пример №6

Докажите, что две окружности касаются внутренним образом тогда и только тогда, когда расстояние между их центрами равно модулю разности их радиусов.

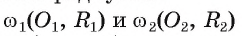
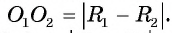
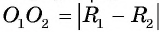
Другими словами, если окружности касаются внутренним образом, то И наоборот, если выполняется равенство , то окружности касаются внутренним образом.

Пример №7

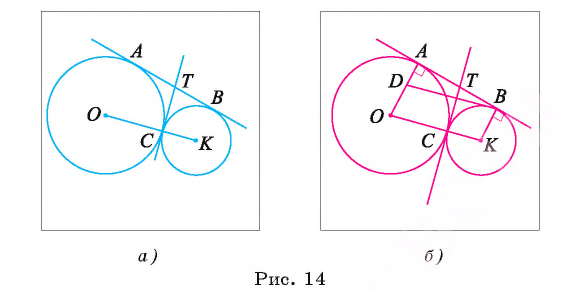
Две окружности с центрами в точках О и К, радиусы которых равны 16 см и 9 см соответственно, касаются внешним образом в точке С. К окружностям проведена общая касательная АВ, где точки А и В — точки касания.

Общая касательная, проведенная через точку С, пересекает касательную АВ в точке Т (рис. 14, а). Вычислите длину отрезка СТ.

Решение:

Для решения задачи воспользуемся тем, что отрезки касательных, проведенные к окружности из одной точки, равны, а радиусы, проведенные в точку касания, перпендикулярны касательной. Учтем также, что окружности касаются внешним образом, а значит, расстояние между их центрами равно сумме их радиусов.

1) Так как отрезки касательных к окружности, проведенные из одной точки, равны, то ТС = ТА = ТВ, т. е. 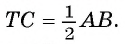. Значит, нам необходимо вычислить длину отрезка АВ.

2) Так как окружности касаются внешним образом, то ОК = ОС + СК = 16 + 9 = 25 (см).

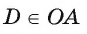
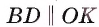
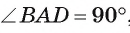
3) Рассмотрим четырехугольник ODBK. Пусть и (рис. 14, б). Так как радиус, проведенный в точку касания, перпендикулярен касательной, то, т. е. треугольник BAD — прямоугольный. Следовательно,

Тогда 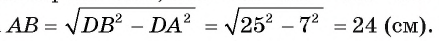Следовательно,

Центральные и вписанные углы

В данном параграфе изучим понятия центрального и вписанного углов.

Определение. Центральным углом окружности называется угол с вершиной в центре этой окружности.

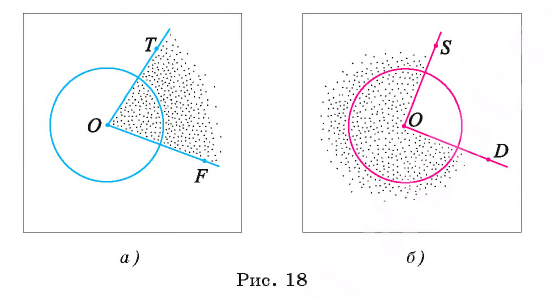
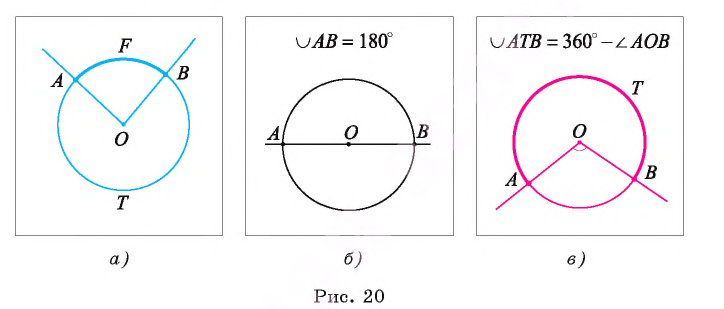
Например, на рисунке 18, а изображен центральный угол TOF, который меньше развернутого угла, а на рисунке 18, б — центральный угол SOD — больше развернутого угла.

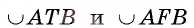
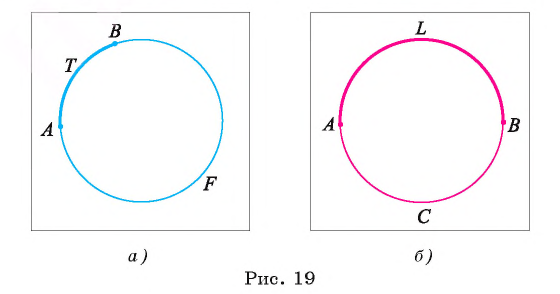
Любые две различные точки А и В окружности служат концами двух дуг. Для различия этих дуг на каждой из них отмечается некоторая промежуточная точка. Например, если на дугах отмечены точки F и Т, то в этом случае дуги обозначаются и данная запись читается так: «дуга АТВ и дуга AFB» (рис. 19, а). Если понятно, о какой из двух дуг идет речь, употребляется также обозначение

Дуга АВ окружности называется полуокружностью, если ее концы служат концами диаметра этой окружности.

Например, на рисунке 19, б изображены полуокружности ALB и АС В.

Пусть точки А и Б не являются концами диаметра окружности с центром в точке О. Тогда лучи ОА и ОБ служат сторонами двух центральных углов, один из которых меньше, а другой больше развернутого угла (рис. 20, а).

Дуга АВ окружности 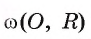и центральный угол АОВ, внутри которого лежит эта дуга, называются соответствующими.

Если дуга окружности лежит внутри соответствующего ей центрального угла, который меньше развернутого угла, то говорят, что эта дуга меньше полуокружности.

Если дуга окружности лежит внутри соответствующего ей центрального угла, который больше развернутого угла, то говорят, что дуга больше полуокружности.

Например, на рисунке 20, а изображены дуга AFB, которая меньше полуокружности, и дуга АТВ — больше полуокружности.

Для сравнения дуг окружности вводится понятие градусной меры дуги окружности.

Дадим определение градусной меры дуги окружности.

Определение. Градусной мерой дуги окружности называется градусная мера соответствующего ей центрального угла.

Градусная мера дуги АВ, как и сама дуга, обозначается

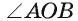
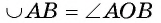
Таким образом, если дуга АВ окружности меньше полуокружности, a — соответствующий ей центральный угол, то (см. рис. 20, а).

Если дуга АВ является полуокружностью, то ее градусная мера равна 180° (рис. 20, б).

Градусная мера дуги АТВ, которая больше полуокружности и дополняет дугу АВ, меньшую полуокружности, до окружности, равна 360° 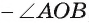, где угол АОВ соответствует дуге АВ (рис. 20, в).

Понятие градусной меры дуги позволяет определить понятие равенства дуг окружности.

Две дуги одной и той же окружности называются равными, если равны их градусные меры.

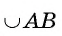
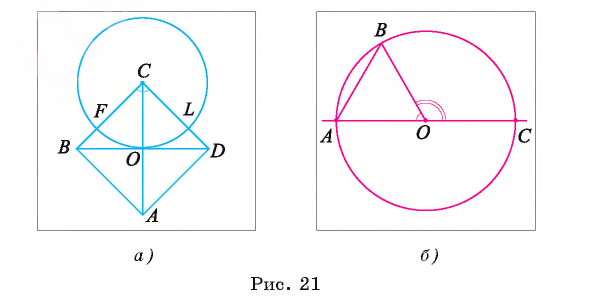
Если градусная мера дуги АВ равна 33°, то пишут = 33°. Читают: «Градусная мера дуги АВ равна 33°», или кратко «Дуга АВ равна 33°».

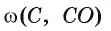
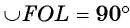
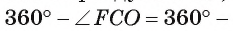
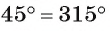
Рассмотрим примеры. Пусть диагонали квадрата ABCD пересекаются в точке О. Окружность пересекает стороны ВС и CD квадрата в точках F и L соответственно. Тогда , а градусная мера дуги FO, которая меньше полуокружности, равна 45°. Градусная мера дуги FLO, которая больше полуокружности, равна (рис. 21, а).

Рассмотрим еще один пример. Пусть точка О — центр окружности, отрезок АВ — хорда окружности, равная ее радиусу, а отрезок АС — диаметр окружности (рис. 21, б).

Тогда градусная мера дуги АВ, которая меньше полуокружности, равна 60°, так как треугольник АОВ — равносторонний, а значит, градусная мера соответствующего ей центрального угла АОВ равна 60°. Градусная мера дуги ВС, которая меньше полуокружности, равна 120°, так как градусная мера соответствующего ей центрального угла ВОС равна 120°.

Можем вычислить градусную меру дуги ВАС, которая больше полуокружности: 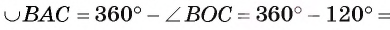= 240°.

Вписанные углы. Рассмотрим понятие вписанного угла

Определение. Угол называется вписанным в окружность, если он меньше развернутого угла, вершина его лежит на окружности, а стороны пересекают эту окружность.

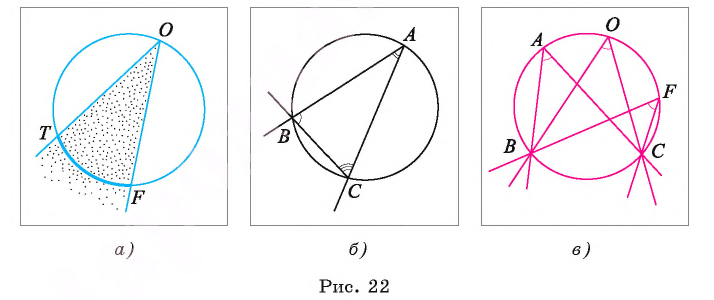
Например, на рисунке 22, а изображен вписанный угол TOF. Если точки А, В и С лежат на окружности, то каждый из угол ABC, ВСА, САВ является вписанным (рис. 22, б).

Пусть 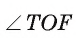— вписанный угол, при этом Г и В — точки пересечения его сторон с окружностью, a TF — дуга, которая лежит внутри этого вписанного угла. В этом случае говорят, что вписанный угол TOF опирается на дугу TF (см. рис. 22, а).

Например, на рисунке 22, в изображены вписанные углы ВАС, ВОС и BFC, которые опираются на одну и ту же дугу ВС.

Теперь докажем теорему о вписанном угле.

Теорема 1(о вписанном угле). Градусная мера вписанного угла равна половине градусной меры, дуги, на которую он опирается.

Пусть вписанный в окружность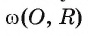угол ABC опирается на дугу АС.

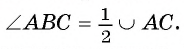
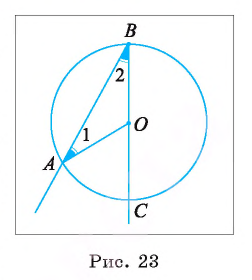
Докажем, что Рассмотрим три возможных случая. Центр О окружности лежит: 1) на одной из сторон угла; 2) во внутренней области угла; 3) во внешней области угла.

Первый случай. Центр О окружности лежит на одной из сторон угла ABC, например на стороне ВС (рис. 23).

1) Дуга АС меньше полуокружности, следовательно,

2) Угол АОС — внешний угол равнобедренного треугольника АОВ, значит,

3) Так как углы при основании равнобедренного треугольника АОВ равны, то

4) Так как 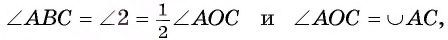, то

Второй случай. Центр О окружности лежит во внутренней области угла.

1) Пусть D — точка пересечения луча ВО и дуги АС (рис. 24). Тогда по доказанному в первом случае

Таким образом,

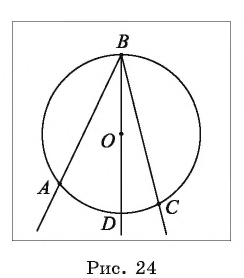
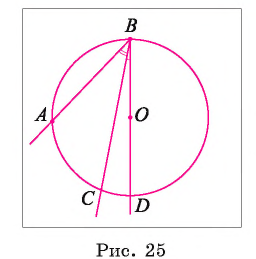
Третий случай. Центр О окружности лежит во внешней области угла ABC.

1) Пусть D — точка пересечения луча ВО с окружностью (рис. 25). Тогда согласно доказанному в первом случае

Таким образом,

Из данной теоремы получим следующие следствия.

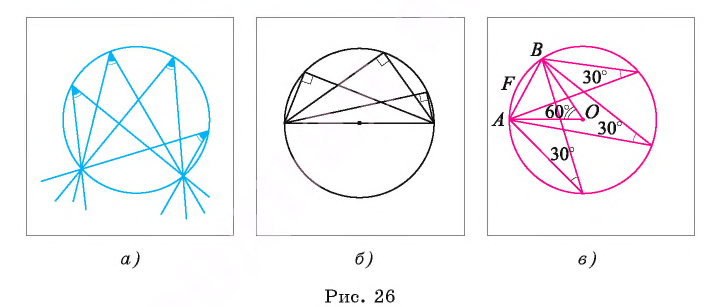
Следствие 1. Вписанные углы, опирающиеся на одну и ту же дугу, равны (рис. 26, а).

Следствие 2. Вписанный угол, опирающийся на полуокружность, прямой (рис. 26, б).

Рассмотрим пример. Пусть хорда АВ соединяет концы дуги AFB и равна радиусу окружности со (О, R). Тогда градусная мера каждого из вписанных углов, опирающихся на дугу AFB, равна 30° (рис. 26, в). Действительно, градусная мера центрального угла АОВ равна 60°, значит, 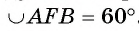. Каждый из указанных углов опирается на дугу AFB, следовательно, градусная мера каждого из них равна

Теорема 2 (об угле между хордой и касательной).

Градусная мера угла, сторонами которого служат касательная и хорда, равна половине градусной меры дуги, расположенной внутри этого угла.

Доказательство.

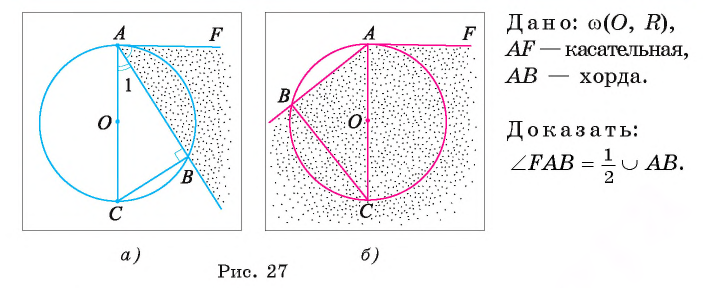
Первый случай. Пусть угол FAB — острый (рис. 27, о.).

1) Проведем диаметр АС. Тогда вписанный угол СВ А опирается на полуокружность, значит, по следствию 2 он прямой, т. е.

2) Треугольник СВА — прямоугольный, следовательно,

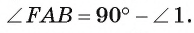
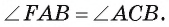
3) Так как диаметр АС перпендикулярен касательной FA, то Таким образом, Так как вписанный угол АСВ опирается на дугу

Следовательно,

Второй случай. Пусть угол FAB — тупой (рис. 27, б). Проведем диаметр СА. Тогда

но дуга ВСА лежит внутри тупого угла FAB.

Свойство пересекающихся хорд. Теорема о касательной и секущей

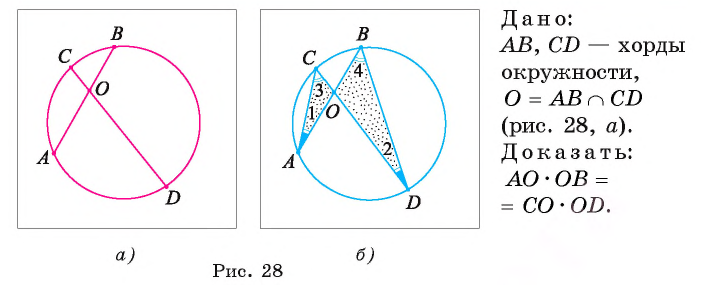
Теорема 3 (об отрезках пересекающихся хорд). Если две хорды окружности пересекаются, то произведение длин отрезков одной хорды равно произведению длин отрезков другой хорды.

1) Проведем хорды АС и BD (рис. 28, б). Рассмотрим треугольники АОСи DOB.

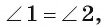
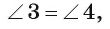
2) Заметим, что так как они вписанные и опираются на одну и ту же дугу СВ. Кроме того, , так как они вписанные и опираются на одну и ту же дугу AD.

3) Треугольник АОС подобен треугольнику DOB по первому признаку подобия треугольников, так как 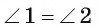и

4) Из подобия треугольников АОС и DOB следует, что

Значит,

Пусть через точку S, лежащую вне окружности, проведена секущая, которая пересекает окружность в точках С и Б, и SC

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник