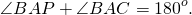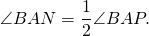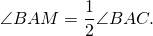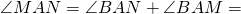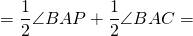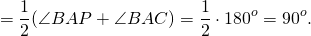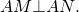что такое внешняя биссектриса
Биссектриса внешнего угла треугольника
Чему равен угол, который образует биссектриса внешнего угла треугольника с биссектрисой смежного ему внутреннего угла?
Биссектриса внешнего угла треугольника перпендикулярна биссектрисе смежного с ним внутреннего угла.

∠BAP — внешний угол при вершине A,
AN — биссектриса ∠BAP,
AM — биссектриса ∠BAC.
Доказательство: (аналогично доказательству об угле между биссектрисами смежных углов).
Так как внешний угол треугольника — это угол, смежный с внутренним углом при данной вершине, то по свойству смежных углов
Так как AN — биссектриса внешнего угла BAP, то
Так как AM — биссектриса угла BAC, то
Итак, мы доказали, что биссектриса внешнего угла треугольника образует с биссектрисой внутреннего угла при данной вершине прямой угол:
Вывод: если требуется найти угол между биссектрисами внешнего и внутреннего углов треугольника, знать градусные меры самих углов не требуется. Каким бы ни был внешний угол треугольника, его биссектриса перпендикулярна биссектрисе смежного внутреннего угла.
4 Comments
докажите что биссектриса внешнего угла противоположного основанию равнобедренного треугольника параллельна основатию этого угла
Решите пожалуйста. Один из углов треугольника равен альфа. Найдите угол между биссектрисами внешних углов, проведённых из вершин двух других углов.
Элементы треугольника. Биссектриса
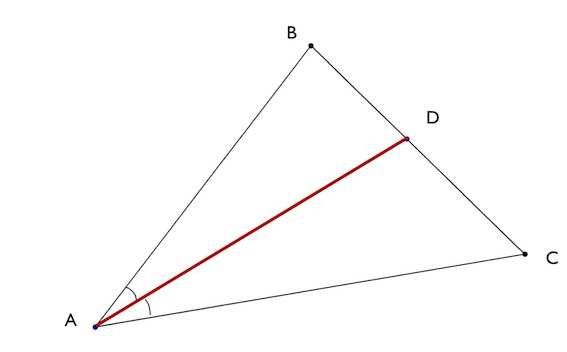
Биссектриса треугольника – отрезок биссектрисы угла треугольника, заключенный между вершиной треугольника и противолежащей ей стороной.
Свойства биссектрисы
1. Биссектриса треугольника делит угол пополам.
2. Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон ()
3. Точки биссектрисы угла треугольника равноудалены от сторон этого угла.
4. Биссектрисы внутренних углов треугольника пересекаются в одной точке — центре вписанной в этот треугольник окружности.
Некоторые формулы, связанные с биссектрисой треугольника
(доказательство формулы – здесь)
, где
— длина биссектрисы, проведённой к стороне
,
— стороны треугольника против вершин
соответственно,
— длины отрезков, на которые биссектриса
делит сторону
,
Приглашаю посмотреть видеоурок, в котором демонстрируется применение всех указанных выше свойств биссектрисы.
Задачи, рассматриваемые в видеоролике:
1.В треугольнике АВС со сторонами АВ=2 см, ВС=3 см, АС=3 см проведена биссектриса ВМ. Найти длины отрезков АМ и МС
2. Биссектриса внутреннего угла при вершине А и биссектриса внешнего угла при вершине С треугольника АВС пересекаются в точке М. Найдите угол BMC, если угол В равен 40, угол С – 80 градусов
3. Найти радиус окружности, вписанной в треугольник, считая стороны квадратных клеток равными 1
Возможно, вам будет интересен и этот небольшой видеоурок, где применяется одно из свойств биссектрисы
Чтобы не потерять страничку, вы можете сохранить ее у себя: