что такое внешний угол треугольника 7 класс геометрия

Внешний угол треугольника

Внешний угол треугольника — это угол, смежный с любым из внутренних углов треугольника.

При каждой вершине треугольника может быть построено по два равных внешних угла. Например, если продолжить все стороны треугольника ABC, то при каждой его вершине получится по два внешних угла, которые равны между собой, как вертикальные углы:

Из данного примера можно сделать вывод, что внешние углы, построенные при одной вершине, будут равны.

Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.

Так как внешний угол (∠1) дополняет внутренний угол (∠4) до развёрнутого угла, то их сумма равна 180°:

Сумма внутренних углов углов любого треугольника тоже равна 180°, значит:

Из этого следует, что

Сократив обе части полученного равенства на одно и тоже число (∠4), получим:

Из этого можно сделать вывод, что внешний угол треугольника всегда больше любого внутреннего угла, не смежного с ним.

Сумма внешних углов

Сумма трёх внешних углов треугольника, построенных при разных вершинах, равна 360°

Рассмотрим треугольник ABC:

Каждая пара углов (внутренний и смежный с ним внешний) в сумме равны 180°. Все шесть углов (3 внутренних и 3 внешних) вместе равны 540°:

(∠1 + ∠4) + (∠2 + ∠5) + (∠3 + ∠6) = 180° + 180° + 180° = 540°.

Значит чтобы найти сумму внешних углов, надо из общей суммы вычесть сумму внутренних углов:

Источник

Внешний угол треугольника

Углы треугольника бывают внутренние и внешние. Что такое внешний угол треугольника? Как его найти?

Внешний угол треугольника при данной вершине — это угол, смежный с внутренним углом треугольника при этой вершине.

Как построить внешний угол треугольника? Нужно продлить сторону треугольника.

∠3 — внешний угол при вершине А,

∠2 — внешний угол при вершине С,

∠1 — внешний угол при вершине В.

Сколько внешних углов у треугольника?

При каждой вершине треугольника есть два внешних угла. Чтобы построить внешний угол при вершине треугольника, можно продлить любую из двух сторон, на которых лежит данная вершина. Таким образом получаем 6 внешних углов.

Внешние углы каждой пары при данной вершины равны между собой (как вертикальные):

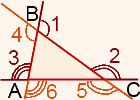
Поэтому, когда говорят о внешнем угле треугольника, не важно, какую из сторон треугольника продлили.

Чему равен внешний угол?

Теорема (о внешнем угле треугольника)

Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

Дано : ∆АВС, ∠1 — внешний угол при вершине С.

∠1 и ∠С (∠АСВ) — смежные, поэтому их сумма равна 180º, значит, ∠1=180º-∠С=180º-(180º-(∠А+∠В))=180º-180º+(∠А+∠В)=∠А+∠В.

Источник

Свойства внешнего угла треугольника

Всего получено оценок: 160.

Всего получено оценок: 160.

Внешний угол треугольника редко используется при решении геометрических задач. Однако при этом свойства внешнего угла лучше знать, потому как задача на применение этих свойств рано или поздно попадется каждому ученику.

Внешний угол

Внешний угол треугольника это угол, смежный с внутренним. Внутренних углов в треугольнике три, и их сумма равна 180 градусам. Смежными углами зовутся углы, одна из сторон каждого лежит на одной прямой, а вторая является общей.

Что нужно сделать, чтобы увидеть внешний угол треугольника? Для этого придется выполнить некоторые дополнительные построения. Чтобы увидеть внешний угол треугольника необходимо продолжить его сторону. При каждой вершине две стороны, соответственно продолжить можно две прямых, и смежных углов будет два.

Итого в треугольнике получается 6 внешних углов.

Нежелательно на рисунке строить два внешних угла при одной вершине одновременно. Это усложнит построение и, чаще всего, не принесет никакого положительного результата.

Свойства внешних углов

Свойств у внешних углов треугольника не так много и все они связаны с определением внешнего угла.

Основное свойство гласит, что внешний угол треугольника равен сумме двух внутренних углов не смежных с ним. Свойство доказывается достаточно просто. Сумма смежных углов равна 180. Сумма углов в треугольнике все те же 180. Тогда, если обозначить внутренние углы а,в,с, внешний угол d, то:

Вычтем из первого выражения второе и получим:

d=в+с – вот и все доказательство.

Рис. 2. Рисунок к доказательству.

Есть еще несколько дополнительных свойств внешних углов:

Особенное значение имеют внешние углы при решении тупоугольных треугольников. Дело в том, что в тупоугольном треугольнике одна из высот всегда внешняя. Найти эту высоту можно через тригонометрические функции. Для этого и нужно знать угол, который для тупоугольного треугольника будет внешним, а для достроенного прямоугольного треугольника – внутренним.

Что мы узнали?

Мы привели определение внешнего угла треугольника. Посчитали количество внешних углов треугольника, определили особенности построения внешних углов при решении задачи. Рассказали, где чаще всего применяются свойства внешних углов треугольника.

Источник

Геометрия. 7 класс

Конспект урока

Перечень рассматриваемых вопросов:

Треугольник – геометрическая фигура, образованная тремя точками, не лежащими на одной прямой, которые соединены между собой отрезками.

Периметр треугольника – это сумма длин всех его сторон.

Стороны треугольника– отрезки, соединяющие вершины треугольника.

Равные треугольники –треугольники, которые можно совместить наложением.

1. Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.

Теоретический материал для самостоятельного изучения.

Вы уже познакомились с основными геометрическими фигурами:

Рассмотрим геометрическую фигуру, которая также является одной из основополагающих– треугольник.

Треугольник – геометрическая фигура, образованная тремя точками, не лежащими на одной прямой, которые соединены между собой отрезками.

Точки, с которых начиналось построение, называются вершинами треугольника.

Отрезки, соединяющие вершины треугольника, называются сторонами треугольника.

А, В, С – вершины треугольника АВС.

АВ, ВС, СА – стороны треугольника АВС.

∠А,∠В,∠С – углы треугольника АВС.

Периметр треугольника – это сумма длин всех его сторон.

Рассмотрим виды треугольников.

Их можно разделить по виду и соотношению углов, а также по соотношению сторон.

По углам треугольник может быть:

– остроугольным, если все его углы являются острыми, (т.е. меньше 90°).

– тупоугольным, если один из его углов тупой(т.е. больше 90°).

– прямоугольным, если один угол 90° (т.е. прямой).

По сторонам треугольник бывает:

– разносторонний, если все его стороны имеют различную длину;

– равнобедренный, если две его стороны равны между собой;

– равносторонний,если у него все три стороны равны между собой.

Напомним, что две фигуры, в том числе и треугольник, можно сравнить. ∆ АВС = ∆ А₁В₁С₁

Два треугольника называются равными, если их можно совместить наложением. При этом попарно совмещаются вершины, углы и стороны треугольников.

Следует помнить, что если два треугольника равны, то элементы (стороны и углы) одного треугольника соответственно равны элементам (сторонам и углам) другого треугольника.

Свойство равных треугольников.

В равных треугольниках против соответственно равных сторон лежат равные углы. Обратное утверждение тоже верно: против соответственно равных углов лежат равные стороны.

Равенство треугольников также можно установить, не производя наложения фигур друг на друга, а сравнивая лишь некоторые элементы этих фигур. Это станет возможным при изучении признаков равенства треугольников.

Внешний угол треугольника.

Введём определение внешнего угла треугольника.

Внешним углом треугольника при данной вершине называется угол, смежный с углом треугольника при этой вершине.

У каждого угла треугольника есть два угла, смежных с ним, т.е. у треугольника шесть внешних углов.

Отметим, что при одной вершине внешние углы равны, как вертикальные.

Разбор решения заданий тренировочного модуля.

Найдите градусную меру внешнего ∠В, треугольника АВС, если ∠АВС = 60°.

По рисунку видно, что угол В внешний угол треугольника и он является смежным к углу АВС, следовательно, их сумма равна 180°.

∠В = 180° – ∠АВС = 180° – 60° = 120°

Периметр ∆АВС равен 58 см, сторона АВ = 20 см, сторона ВС >АС на 5 см. Найдите стороны ВС и АС.

Решение: Для решения задачи воспользуемся формулой периметра треугольника Р_∆АВС = АВ + ВС + АС. Обозначим сторону АС за х, тогда сторона ВС равна х + 5, составим уравнение.

5. х = 16,5 см – сторона АС.

6. 16,5 + 5 = 21,5 см – сторона ВС.

Источник

Урок и презентация к уроку геометрии в 7 классе «Внешний угол треугольника. Сумма углов треугольника»

Ищем педагогов в команду «Инфоурок»

Выбранный для просмотра документ на урок сум углов треугол.ppt

Описание презентации по отдельным слайдам:

«Я слышу – я забываю, я вижу – я запоминаю, я делаю – я усваиваю». Китайская мудрость.

I в. (остроугольный) А= B= C= А+ В+ С= А= B= C= А+ В+ С= А= B= C= А+ В+ С= А= B= C= А+ В+ С= II в. (прямоугольный) III в. (равнобедренный) IV (тупоугольный)

2 Теорема: Сумма углов треугольника равна 180. Дано: ∆ ABC Доказательство: 1)Провед.прямую а || AC 2) 4 =1 5 = 3 3) Т.к. 4+2+5=180, то 1+2+3=180 или A+B+C=180 A Доказать: А+B+C=180 C B

…Как для смертных истина ясна, Что в треугольник двум тупым не влиться. Данте А.

В первой книге «Начал» Евклид излагает другое доказательство теоремы о сумме углов треугольника, которое легко понять при помощи чертежа. Евклид 365 –300 г.г. до н.э.

Задачи на готовых чертежах.

Задача № 2 60° 60° 60°

Задача из учебника.

Домашнее задание. § 12, п.1, № 148,149 №154 (по желанию)

Выбранный для просмотра документ открытый урок.doc

Тема: Внешний угол треугольника. Сумма внутренних углов треугольника.

Цели урока:

1. Обучающие:

С помощью эксперимента учащиеся сами сформулируют теорему о сумме углов треугольника, докажут ее и будут применять полученные знания в решении задач, познакомятся с понятием внешнего угла треугольника.

Обобщат знания свойств и признаков параллельных прямых

Продолжат работу по формированию навыка решения задач по готовым чертежам.

2. Развивающие:

Будут развивать математическую речь, умение выполнять сравнение, использовать элементы исследования.

3. Воспитательные:

воспитывать творческую активность, культуру общения, интерес к предмету.

Тип урока: комбинированный

Ресурсы: интерактивная доска, компьютерная презентация, индивидуальные и практические задания

«Я слышу – я забываю, я вижу – я запоминаю, я делаю – я усваиваю»
Китайская мудрость

Сегодня наш класс превратится в научно-исследовательскую лабораторию, а вы станете его сотрудниками. И мы не только познакомимся с работой научно-исследовательского института, но и сами будем делать открытия!

И так: научно-исследовательский институт имеет подразделения:

1. Лаборатория экспериментов.

2.Лаборатория научных доказательств.

3. Лаборатория испытаний.

На предыдущих уроках мы с вами изучали признаки параллельности прямых и свойства углов при параллельных прямых. И сегодня на уроке, полученные по этой теме знания, помогут сделать открытие.

1). Дайте определение параллельных прямых.

(Две прямые на плоскости называется параллельными, если они не пересекаются)

2). Назовите по рис. пары углов, которые образуются при пересечении двух параллельных прямых секущей.

3). Сформулируйте признаки параллельности прямых.

4). Сформулируйте свойства углов при параллельных прямых.

(Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны; Если две параллельные прямые пересечены секущей, то соответственные углы равны; Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 180 0 )

5) Сформулируйте определение треугольника.

(ТРЕУГОЛЬНИК – это фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков соединяющих эти точки, а также части плоскости, ограниченной этими отрезками.)

6) Назовите элементы треугольника. (Вершины, стороны, углы)

7) Какие треугольники различают? (По сторонам: разносторонние, равносторонние, равнобедренные; уметь начертить)

8) А по углам? (остроугольные, тупоугольные, прямоугольные).

9) Каким прибором измеряют углы? ( транспортиром) слайд

Лаборатория экспериментов

Каким путем можно узнать, чему равна сумма углов треугольника? Практически — измерение, теоретически — рассуждением

На доске размещены треугольники(на слайдах), которые предложены ребятам для работы.

Ребята, у вас на столах лежат карточки с изображением треугольников по вариантам.

1 вариант – остроугольный треугольник

2 вариант- прямоугольный треугольник

3 вариант – равнобедренный треугольник

Все ребята на местах (по вариантам) с помощью транспортира измеряют углы треугольников, записывают свои измерения и находят сумму углов треугольника.

Так чему равна сумма углов остроугольного треугольника(1вар)? Итак, Я записываю на доске ваши результаты. И т.д

На столах у вас лежат треугольники. Путем перегибания соберем углы треугольника в одну точку.(демонстрирую)

Что вы заметили? Какой угол получился? (развернутый). Скольким градусам он равен? (180). А из чего он состоит? (из суммы трех углов треугольника) Какой можно сделать вывод?

Вывод: практическая работа показала, что сумма углов любого треугольника равна 180°.

Лаборатория научных доказательств.

А теперь перейдем в лабораторию доказательств и здесь мы с вами докажем научно, что это действительно так.

Запишите в тетрадях число и тему урока: «Сумма углов треугольника»

Запишем формулировку нашего открытия – теорему.

Повторить план доказательства:

— провести прямую через одну из вершин параллельно противолежащей стороне;

— составить пары равных углов;

— представить развернутый угол в виде суммы углов;

— заменить слагаемые равными им углами треугольника.

Обратите внимание на чертёж. Какой мы рассматривали треугольник ( по углам)? Запомните, что у остроугольного треугольника все углы острые. Могут ли в треугольнике быть два прямых или два тупых угла и почему? (Слайд13).

Исторические сведения. Теорема о сумме углов треугольника приписывается многим, в том числе древнегреческим ученым Евклиду и Пифагору. (слайды).

Определение: Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника.

Сколько внешних углов можно построить у любого треугольника?

Докажем, что внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.

Лаборатория испытаний (практическое применение)

Переходим в лабораторию испытаний, посмотрим как применяется теорема на практике при решении задач

4. Закрепление нового материала:

а). Решение задач на готовых чертежах. (Cлайды19-26).

После устного рассмотрения задач в тетрадях записываются некоторые выводы:

б). Решение задач из учебника №153, (Слайды 21.)

в) Самостоятельная работа с проверкой:

Задание № 2. Чему равна сумма углов ABC? Верно ли это?(подумать и объяснить)

г). Можно ли измерить углы любого треугольника?

Это вопрос-шутка, т.к. существует Бермудский треугольник, находящийся в Атлантическом океане между Бермудскими островами, государством Пуэрто-Рико и полуостровом Флорида, у которого невозможно измерить углы. А ещё его называют «дьявольский треугольник», «треугольник проклятых». Загадочность его заключается в том, что в нём бесследно исчезают корабли и самолёты. Природа «бермудского треугольника» остаётся тайной и по сей день.

Источник