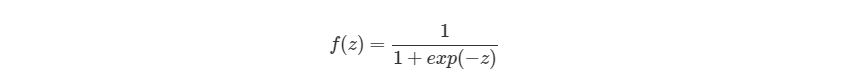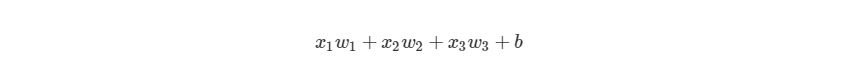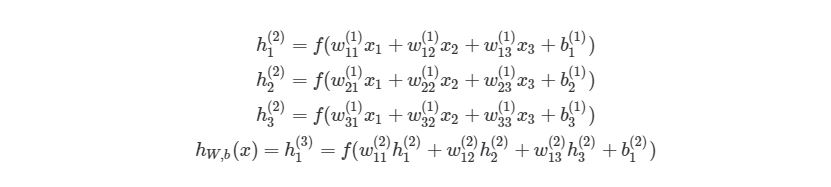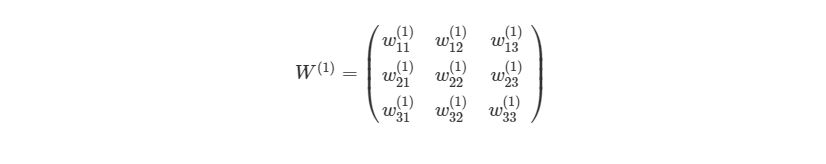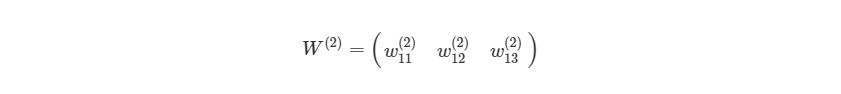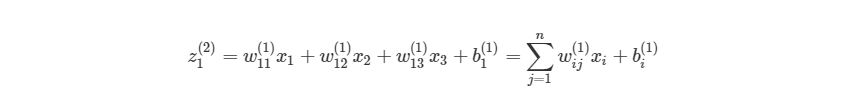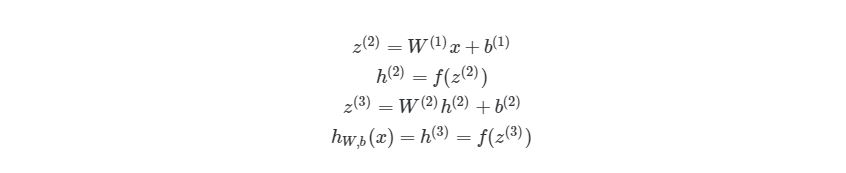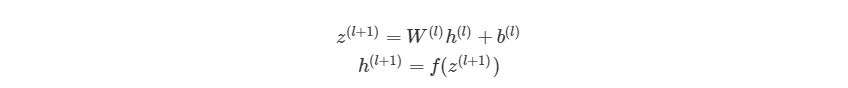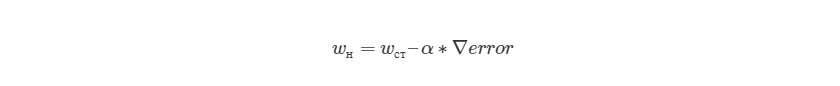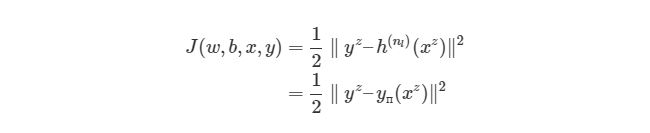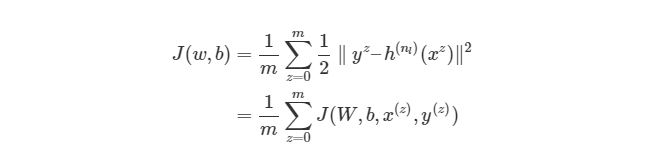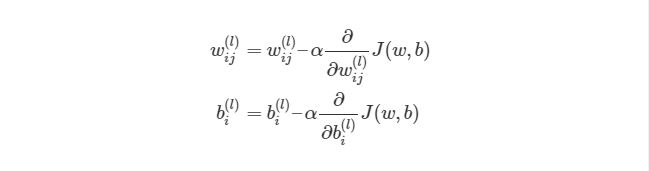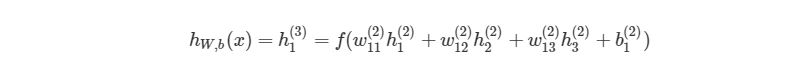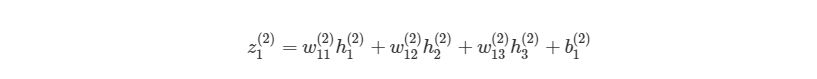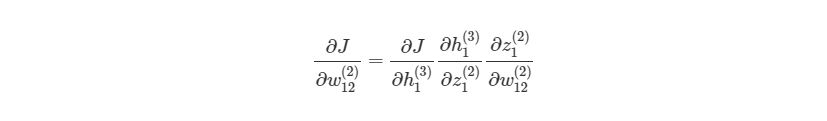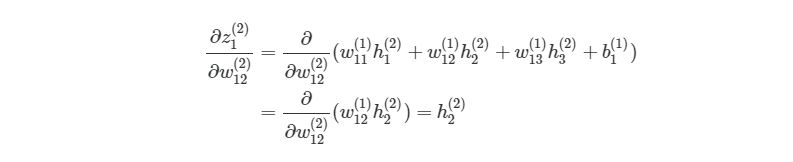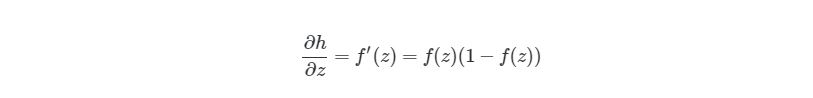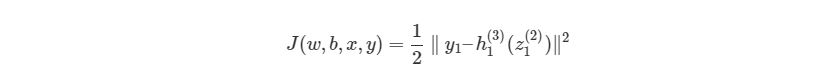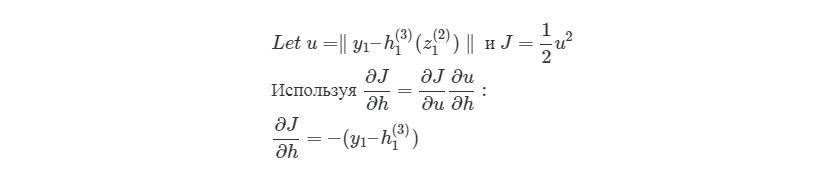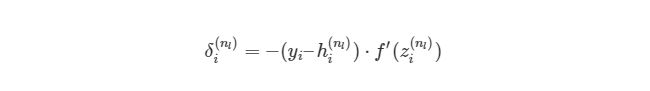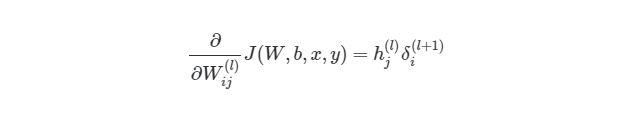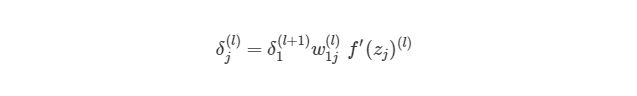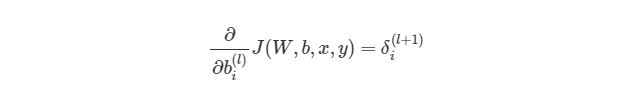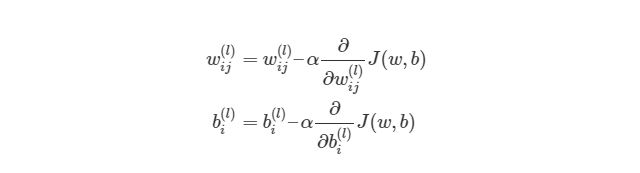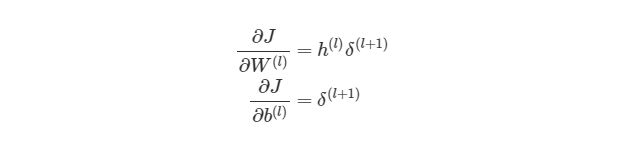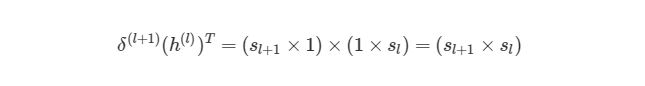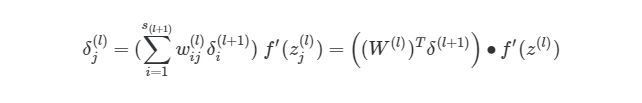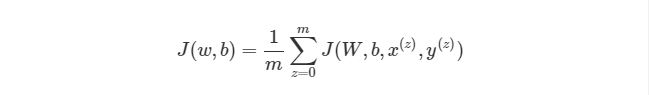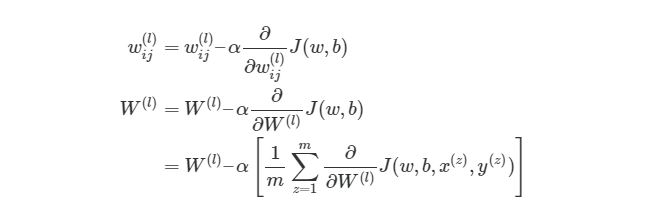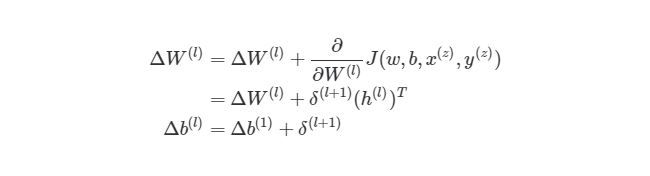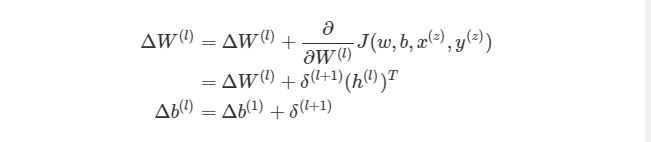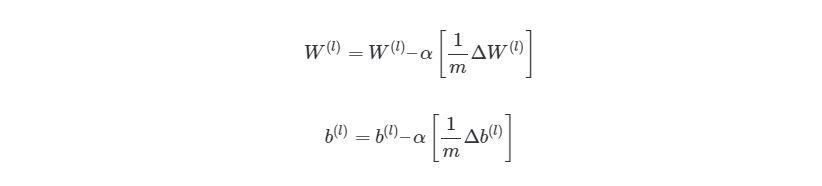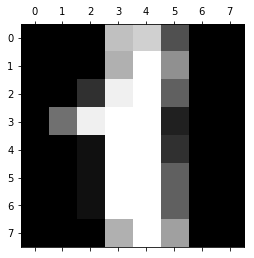что такое веса в нейросети

Инициализация веса в нейронных сетях: путь от основ к каймингу

Дата публикации Apr 3, 2019

Я хотел бы пригласить вас присоединиться ко мне в исследовании различных подходов к инициализации весов слоев в нейронных сетях. Шаг за шагом, через различные короткие эксперименты и мыслительные упражнения, мы узнаем, почему адекватная инициализация веса так важна для тренировки глубоких нейронных сетей. По пути мы рассмотрим различные подходы, предложенные исследователями на протяжении многих лет, и, наконец, подробно рассмотрим, что лучше всего подходит для современных сетевых архитектур, с которыми вы, скорее всего, будете работать.

Примеры для подражания взяты из моего собственногоповторное внедрениеиз набора тетрадей, которыеДжереми Ховардпокрыты вПоследняя версиякурса Deep.ai Deep Learning Part II, в настоящее времяпроводится весной 2019 года в Институте данных USF,

Зачем инициализировать веса

Целью инициализации веса является предотвращение взрыва или исчезновения выходов активации слоя во время прямого прохода через глубокую нейронную сеть. Если это произойдет, градиенты потерь будут либо слишком большими, либо слишком малыми, чтобы выгодно течь в обратном направлении, и сети потребуется больше времени для конвергенции, если она вообще сможет это сделать.

Умножение матриц является основной математической операцией нейронной сети. В глубоких нейронных сетях с несколькими слоями один прямой проход просто влечет за собой выполнение последовательных умножений матриц на каждом слое, между входами этого слоя и матрицей весов. Продукт этого умножения на одном слое становится входом следующего слоя и так далее, и так далее.

Для быстрого и грязного примера, который иллюстрирует это, давайте представим, что у нас есть векторИкскоторый содержит некоторые сетевые входы. При обучении нейронных сетей общепринятая практика заключается в том, чтобы значения наших входных данных масштабировались так, чтобы они попадали в такое нормальное распределение со средним значением 0 и стандартным отклонением 1.

Давайте также притворимся, что у нас есть простая 100-слойная сеть без активаций, и что каждый слой имеет матрицу который содержит веса слоя. Чтобы завершить один прямой проход, нам нужно будет выполнить матричное умножение между входами слоев и весами на каждом из ста слоев, что в итоге составит100последовательные матричные умножения.

Оказывается, что инициализация значений весов слоев из того же стандартного нормального распределения, к которому мы масштабировали наши входные данные, никогда не была хорошей идеей. Чтобы понять почему, мы можем смоделировать прямой проход через нашу гипотетическую сеть.

Вау! Где-то во время этих 100 умножений выходные данные слоя стали настолько большими, что даже компьютер не смог распознать их стандартное отклонение и среднее значение в виде чисел. На самом деле мы можем точно видеть, как долго это происходило.

Выходы активации взорвались в 29 слоях нашей сети. Мы четко инициализировали наши веса, чтобы быть слишком большими.

В течение вышеупомянутого гипотетического прямого прохода выходы активации полностью исчезали.

Подводя итог, если веса инициализируются слишком большими, сеть не будет хорошо учиться. То же самое происходит, когда веса инициализируются слишком мало.

Как мы можем найти сладкое место?

Помните, что, как упоминалось выше, математика, необходимая для завершения прямого прохода через нейронную сеть, влечет за собой не что иное, как последовательность умножения матриц. Если у нас есть выходYэто произведение умножения матриц между нашим входным векторомИкси весовая матрица каждый элементявYопределяется как

Мы можем продемонстрировать, что на данном уровне матричный продукт наших входовИкси весовая матрица то, что мы инициализировали из стандартного нормального распределения, в среднем будет иметь стандартное отклонение, очень близкое к квадратному корню из числа входных соединений, которое в нашем примере равно √512.

Из этого следует, чтосуммаиз этих 512 продуктов будет иметь среднее значение 0, дисперсию 512 и, следовательно, стандартное отклонение √512.

И именно поэтому в нашем примере выше мы увидели, как выходы нашего слоя взрываются после 29 последовательных умножений матриц. В случае нашей базовой 100-уровневой сетевой архитектуры нам бы хотелось, чтобы на выходе каждого уровня было стандартное отклонение около 1. Это, возможно, позволило бы нам повторять матричные умножения на любом количестве сетевых уровней, как мы хотим. без активаций взрыва или исчезновения.

Если мы сначала масштабируем весовую матрицу путем деления всех случайно выбранных значений на √512, поэлементное умножение, которое заполняет один элемент выходныхYтеперь, в среднем, будет иметь дисперсию всего 1 / √512.

Теперь давайте снова запустим нашу быструю и грязную 100-слойную сеть. Как и прежде, мы сначала выбираем веса слоев случайным образом из стандартного нормального распределения внутри [-1,1], но на этот раз мы масштабируем эти веса на 1 / √N, гдеNколичество сетевых входных подключений на уровне, которое в нашем примере составляет 512

Успех! Наши выходные данные слоя не взорвались и не исчезли, даже после 100 наших гипотетических слоев.

Хотя на первый взгляд может показаться, что на данный момент мы можем назвать это днем, реальные нейронные сети не так просты, как может показаться в нашем первом примере. Для простоты функции активации были опущены. Тем не менее, мы никогда не будем делать это в реальной жизни. Именно благодаря размещению этих нелинейных функций активации в хвостовой части сетевых слоев, глубокие нейронные сети способны создавать близкие приближения сложных функций, которые описывают явления реального мира, которые затем могут быть использованы для создания поразительно впечатляющих предсказаний, такие как классификация образцов почерка.

Xavier Initialization

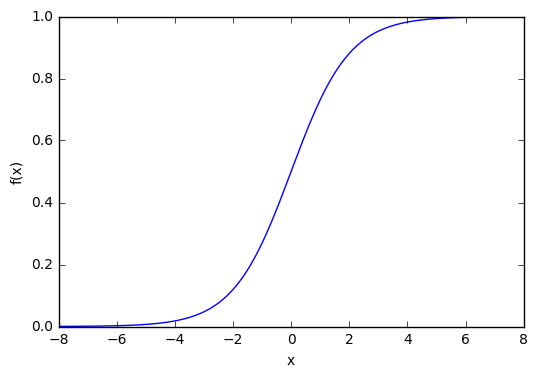
Еще несколько лет назад наиболее часто используемые функции активации были симметричны относительно заданного значения и имели диапазоны, которые асимптотически приближались к значениям, которые были плюс / минус на некотором расстоянии от этой средней точки. Функции гиперболического тангенса и мягкого знака иллюстрируют этот класс активаций.

Мы добавим функцию активации гиперболического тангенса после каждого слоя нашей гипотетической 100-слойной сети, а затем посмотрим, что произойдет, когда мы используем нашу собственную схему инициализации веса, где веса слоя масштабируются на 1 / √п.

Стандартное отклонение выходов активации 100-го уровня составляет около 0,06. Это определенно мало, но, по крайней мере, активации не исчезли полностью!

Насколько интуитивно понятным может показаться, что путь к открытию нашей собственной стратегии инициации веса теперь выглядит ретроспективно, вы можете быть удивлены, узнав, что совсем недавно, в 2010 году, это не был традиционный подход для инициализации слоев веса.

Когда Ксавье Глорот и Йошуа Бенжио опубликовали свою знаменательную статью под названиемПонимание сложности обучения глубоких нейронных сетей с прямой связью«обычно используемая эвристика», с которой они сравнивали свои эксперименты, заключалась в инициализации весов изединообразныйраспределение в [-1,1], а затем масштабирование на 1 / √N,

Оказывается, этот «стандартный» подход не очень хорошо работает.

Эта низкая производительность на самом деле побудила Глорот и Бенжио предложить свою собственную стратегию инициализации веса, которую они назвали «нормализованной инициализацией» в своей статье, и которая сейчас широко известна как «инициализация Ксавье».

Инициализация Xavier устанавливает вес слоя для значений, выбранных из случайного равномерного распределения, которое ограничено

гдеnᵢколичество входящих сетевых подключений, или «разветвление», к уровню, иnᵢ₊₁это количество исходящих сетевых подключений из этого уровня, также называемое «разветвлением».

Глорот и Бенжио полагали, что инициализация веса Ксавье будет поддерживать дисперсию активаций и градиенты с обратным распространением на всем протяжении вверх или вниз по слоям сети. В своих экспериментах они обнаружили, что инициализация Ксавье позволила пятислойной сети поддерживать почти одинаковые отклонения ее градиентов веса по слоям.

И наоборот, оказалось, что использование «стандартной» инициализации привело к гораздо большему разрыву в расхождении между градиентами веса в нижних слоях сети, которые были выше, и в самых верхних слоях, которые приближались к нулю.

Чтобы продемонстрировать это, Глорот и Бенжио продемонстрировали, что сети, инициализированные с помощью Xavier, достигли значительно более быстрой конвергенции и более высокой точности наЗадача классификации изображений CIFAR-10,

Давайте еще раз запустим нашу 100-слойную сеть, на этот раз с помощью инициализации Xavier:

В нашей экспериментальной сети инициализация Xavier выполняется практически идентично самодельному методу, который мы вывели ранее, где мы выбирали значения из случайного нормального распределения и масштабировали по квадратному корню из числа входящих сетевых подключений,N,

Kaiming Initialization

Концептуально, имеет смысл, что при использовании функций активации, которые симметричны относительно нуля и имеют выходы внутри [-1,1], такие как softsign и tanh, мы бы хотели, чтобы выходы активации каждого слоя имели среднее значение 0 и стандартное отклонение в среднем около 1. Это как раз то, что позволяют наш доморощенный метод и Ксавье.

Но что, если мы используем функции активации ReLU? Будет ли еще иметь смысл масштабировать случайные начальные значения веса таким же образом?

Чтобы увидеть, что произойдет, давайте использовать активацию ReLU вместо tanh в одном из слоев нашей гипотетической сети и понаблюдаем за ожидаемым стандартным отклонением ее выходных данных.

Оказывается, что при использовании активации ReLU один слой в среднем будет иметь стандартное отклонение, которое очень близко к квадратному корню из числа входных соединений,делится на квадратный корень из двухили √512 / √2 в нашем примере.

Масштабирование значений весовой матрицы это число приведет к тому, что каждый отдельный уровень ReLU будет иметь стандартное отклонение в среднем 1.

Как мы показали ранее, сохранение стандартного отклонения активаций слоев около 1 позволит нам сложить еще несколько слоев в глубокой нейронной сети без взрыва или исчезновения градиентов.

Это исследование того, как наилучшим образом инициализировать весовые коэффициенты в сетях с активациями, подобными ReLU, послужило мотивацией Kaiming He et. и др. впредложить собственную схему инициализацииэто предназначено для глубоких нейронных сетей, которые используют эти виды асимметричных, нелинейных активаций.

В своей статье 2015 года He et. и др. продемонстрировали, что глубокие сети (например, 22-слойный CNN) будут сходиться намного раньше, если используется следующая стратегия инициализации входного веса:

В качестве окончательного сравнения, вот что произойдет, если мы вместо этого будем использовать инициализацию Xavier.

Ой! При использовании Xavier для инициализации весов, выходы активации почти полностью исчезли к 100-му слою!

Между прочим, когда они обучали даже более глубокие сети, которые использовали ReLU, He et. и др. обнаружил, что 30-слойный CNN, использующий инициализацию Xavier, полностью застопорился и не научился вообще Однако, когда одна и та же сеть была инициализирована в соответствии с трехэтапной процедурой, описанной выше, она имела значительно большую конвергенцию.

Мораль этой истории для нас заключается в том, что любая сеть, которую мы обучаем с нуля, особенно для приложений компьютерного зрения, почти наверняка будет содержать функции активации ReLU и иметь несколько уровней. В таких случаях Kaiming должен быть нашей стратегией инициации.

Да, вы тоже можете быть исследователем

Еще важнее то, что мне не стыдно признать, что я испугался, когда впервые увидел формулы Ксавье и Кайминга. Что с их соответствующими квадратными корнями из шести и двух, часть меня не могла помочь, но я чувствую, что они, должно быть, были результатом некой оракулярной мудрости, которую я не мог понять самостоятельно. И давайте посмотрим правде в глаза, иногда математика в глубоких учебных документах может выглядетьочень похоже на иероглифыкроме как безРозеттский каменьпомочь в переводе

Но я думаю, что путешествие, которое мы совершили, показало нам, что этот откровенный ответ чувства запугивания, хотя он и вполне понятен, отнюдь не неизбежен. Хотя в статьях Кайминга и (особенно) Ксавье действительно содержится значительная доля математики, мы воочию убедились, что экспериментов, эмпирических наблюдений и некоторого простого здравого смысла было достаточно, чтобы вывести основной набор принципов, лежащих в основе того, что в настоящее время является наиболее широко распространенным. используется схема инициализации веса.

Поочередно поставь: если сомневаешься, будь смелым, попробуй и посмотри, что получится!

Источник

Нейронные сети в картинках: от одного нейрона до глубоких архитектур

Многие материалы по нейронным сетям сразу начинаются с демонстрации довольно сложных архитектур. При этом самые базовые вещи, касающиеся функций активаций, инициализации весов, выбора количества слоёв в сети и т.д. если и рассматриваются, то вскользь. Получается начинающему практику нейронных сетей приходится брать типовые конфигурации и работать с ними фактически вслепую.

В статье мы пойдём по другому пути. Начнём с самой простой конфигурации — одного нейрона с одним входом и одним выходом, без активации. Далее будем маленькими итерациями усложнять конфигурацию сети и попробуем выжать из каждой из них разумный максимум. Это позволит подёргать сети за ниточки и наработать практическую интуицию в построении архитектур нейросетей, которая на практике оказывается очень ценным активом.

Иллюстративный материал

Популярные приложения нейросетей, такие как классификация или регрессия, представляют собой надстройку над самой сетью, включающей два дополнительных этапа — подготовку входных данных (выделение признаков, преобразование данных в вектор) и интерпретацию результатов. Для наших целей эти дополнительные стадии оказываются лишними, т.к. мы смотрим не на работу сети в чистом виде, а на некую конструкцию, где нейросеть является лишь составной частью.

Фреймворк

Для демонстрации конфигураций и результатов предлагаю взять популярный фреймворк Keras, написанный на Python. Хотя вы можете использовать любой другой инструмент для работы с нейросетями — чаще всего различия будут только в наименованиях.

Самая простая нейросеть

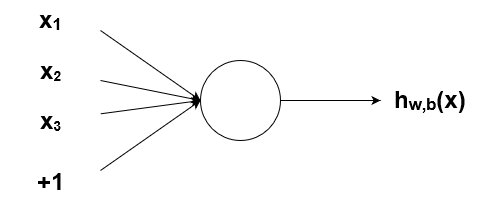
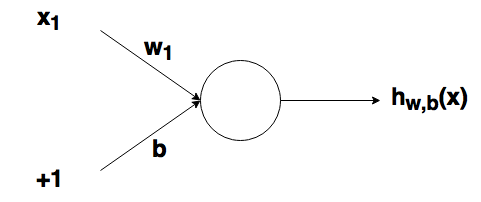
Самой простой из возможных конфигураций нейросетей является один нейрон с одним входом и одним выходом без активации (или можно сказать с линейной активацией f(x) = x):

N.B. Как видите, на вход сети подаются два значения — x и единица. Последняя необходима для того, чтобы ввести смещение b. Во всех популярных фреймворках входная единица уже неявно присутствует и не задаётся пользователем отдельно. Поэтому здесь и далее будем считать, что на вход подаётся одно значение.

Несмотря на свою простоту эта архитектура уже позволяет делать линейную регрессию, т.е. приближать функцию прямой линией (часто с минимизацией среднеквадратического отклонения). Пример очень важный, поэтому предлагаю разобрать его максимально подробно.

Как видите, наша простейшая сеть справилась с задачей приближения линейной функции линейной же функцией на ура. Попробуем теперь усложнить задачу, взяв более сложную функцию:

Опять же, результат вполне достойный. Давайте посмотрим на веса нашей модели после обучения:

Первое число — это вес w, второе — смещение b. Чтобы убедиться в этом, давайте нарисуем прямую f(x) = w * x + b:

Усложняем пример

Хорошо, с приближением прямой всё ясно. Но это и классическая линейная регрессия неплохо делала. Как же захватить нейросетью нелинейность аппроксимируемой функции?

Давайте попробуем накидать побольше нейронов, скажем пять штук. Т.к. на выходе ожидается одно значение, придётся добавить ещё один слой к сети, который просто будет суммировать все выходные значения с каждого из пяти нейронов:

И… ничего не вышло. Всё та же прямая, хотя матрица весов немного разрослась. Всё дело в том, что архитектура нашей сети сводится к линейной комбинации линейных функций:

f(x) = w1′ * (w1 * x + b1) +… + w5′ (w5 * x + b5) + b

Т.е. опять же является линейной функцией. Чтобы сделать поведение нашей сети более интересным, добавим нейронам внутреннего слоя функцию активации ReLU (выпрямитель, f(x) = max(0, x)), которая позволяет сети ломать прямую на сегменты:

Максимальное количество сегментов совпадает с количеством нейронов на внутреннем слое. Добавив больше нейронов можно получить более точное приближение:

Дайте больше точности!

Уже лучше, но огрехи видны на глаз — на изгибах, где исходная функция наименее похожа на прямую линию, приближение отстаёт.

В качестве стратегии оптимизации мы взяли довольно популярный метод — SGD (стохастический градиентный спуск). На практике часто используется его улучшенная версия с инерцией (SGDm, m — momentum). Это позволяет более плавно поворачивать на резких изгибах и приближение становится лучше на глаз:

Усложняем дальше

Синус — довольно удачная функция для оптимизации. Главным образом потому, что у него нет широких плато — т.е. областей, где функция изменяется очень медленно. К тому же сама функция изменяется довольно равномерно. Чтобы проверить нашу конфигурацию на прочность, возьмём функцию посложнее:

Увы и ах, здесь мы уже упираемся в потолок нашей архитектуры.

Дайте больше нелинейности!

Давайте попробуем заменить служивший нам в предыдущих примерах верой и правдой ReLU (выпрямитель) на более нелинейный гиперболический тангенс:

Инициализация весов — это важно!

Приближение стало лучше на сгибах, но часть функции наша сеть не увидела. Давайте попробуем поиграться с ещё одним параметром — начальным распределением весов. Используем популярное на практике значение ‘glorot_normal’ (по имени исследователя Xavier Glorot, в некоторых фреймворках называется XAVIER):

Уже лучше. Но использование ‘he_normal’ (по имени исследователя Kaiming He) даёт ещё более приятный результат:

Как это работает?

Давайте сделаем небольшую паузу и разберёмся, каким образом работает наша текущая конфигурация. Сеть представляет из себя линейную комбинацию гиперболических тангенсов:

f(x) = w1′ * tanh(w1 * x + b1) +… + w5′ * tanh(w5 * x + b5) + b

На иллюстрации хорошо видно, что каждый гиперболический тангенс захватил небольшую зону ответственности и работает над приближением функции в своём небольшом диапазоне. За пределами своей области тангенс сваливается в ноль или единицу и просто даёт смещение по оси ординат.

За границей области обучения

Давайте посмотрим, что происходит за границей области обучения сети, в нашем случае это [-3, 3]:

Как и было понятно из предыдущих примеров, за границами области обучения все гиперболические тангенсы превращаются в константы (строго говоря близкие к нулю или единице значения). Нейронная сеть не способна видеть за пределами области обучения: в зависимости от выбранных активаторов она будет очень грубо оценивать значение оптимизируемой функции. Об этом стоит помнить при конструировании признаков и входных данный для нейросети.

Идём в глубину

До сих пор наша конфигурация не являлась примером глубокой нейронной сети, т.к. в ней был всего один внутренний слой. Добавим ещё один:

Можете сами убедиться, что сеть лучше отработала проблемные участки в центре и около нижней границы по оси абсцисс:

N.B. Слепое добавление слоёв не даёт автоматического улучшения, что называется из коробки. Для большинства практических применений двух внутренних слоёв вполне достаточно, при этом вам не придётся разбираться со спецэффектами слишком глубоких сетей, как например проблема исчезающего градиента. Если вы всё-таки решили идти в глубину, будьте готовы много экспериментировать с обучением сети.

Количество нейронов на внутренних слоях

Просто поставим небольшой эксперимент:

Начиная с определённого момента добавление нейронов на внутренние слои не даёт выигрыша в оптимизации. Неплохое практическое правило — брать среднее между количеством входов и выходов сети.

Источник

Пишем свою нейросеть: пошаговое руководство

Отличный гайд про нейросеть от теории к практике. Вы узнаете из каких элементов состоит ИНС, как она работает и как ее создать самому.

В этой статье будут представлены некоторые понятия, а также немного кода и математики, с помощью которых вы сможете построить и понять простые нейронные сети. Для ознакомления с материалом нужно иметь базовые знания о матрицах и дифференциалах. Код будет написан на языке программирования Python с использованием библиотеки numpy. Вы построите ИНС, используя Python, которая с высокой точностью классифицировать числа на картинках.

1 Что такое искусственная нейросеть?

Неконтролируемое обучение в ИНС пытается «заставить» ИНС «понять» структуру передаваемой входной информации «самостоятельно». Мы не будем рассматривать это в данном посте.

2 Структура ИНС

2.1 Искусственный нейрон

Которая выглядит следующим образом:

2.2 Узлы

Как было упомянуто ранее, биологические нейроны иерархически соединены в сети, где выход одних нейронов является входом для других нейронов. Мы можем представить такие сети в виде соединенных слоев с узлами. Каждый узел принимает взвешенный вход, активирует активационную функцию для суммы входов и генерирует выход.

Круг на картинке изображает узел. Узел является «местоположением» активационной функции, он принимает взвешенные входы, складывает их, а затем вводит их в активационную функцию. Вывод активационной функции представлен через h. Примечание: в некоторых источниках узел также называют перцептроном.

Что такое «вес»? По весу берутся числа (не бинарные), которые затем умножаются на входе и суммируются в узле. Иными словами, взвешенный вход в узел имеет вид:

где w_i— числовые значения веса ( b мы будем обсудим позже). Весы нам нужны, они являются значениями, которые будут меняться в течение процесса обучения. b является весом элемента смещения на 1, включение веса b делает узел гибким. Проще это понять на примере.

2.3 Смещение

Рассмотрим простой узел, в котором есть по одному входу и выходу:

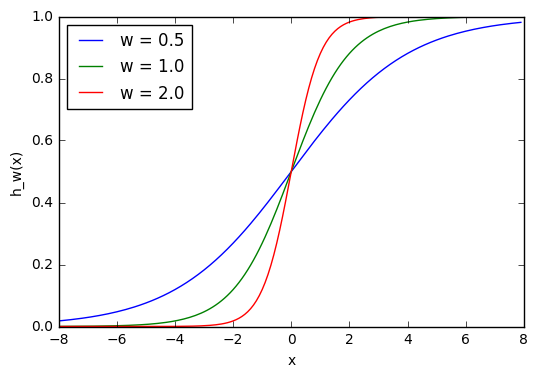
Ввод для активационной функции в этом узле просто x₁w₁. На что влияет изменение в w₁ в этой простой сети?

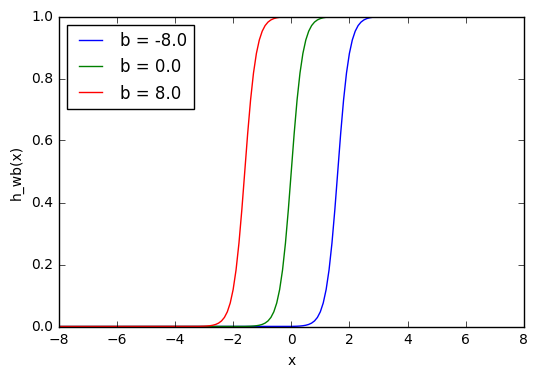
Здесь мы можем видеть, что при изменении веса изменяется также уровень наклона графика активационной функции. Это полезно, если мы моделируем различные плотности взаимосвязей между входами и выходами. Но что делать, если мы хотим, чтобы выход изменялся только при х более 1? Для этого нам нужно смещение. Рассмотрим такую сеть со смещением на входе:

Из графика можно увидеть, что меняя «вес» смещения b, мы можем изменять время запуска узла. Смещение очень важно в случаях, когда нужно имитировать условные отношения.

2.4 Составленная структура

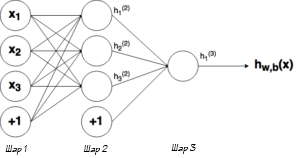
Выше было объяснено, как работает соответствующий узел / нейрон / перцептрон. Но, как вы знаете, в полной нейронной сети находится много таких взаимосвязанных между собой узлов. Структуры таких сетей могут принимать мириады различных форм, но самая распространенная состоит из входного слоя, скрытого слоя и выходного слоя. Пример такой структуры приведены ниже:

2.5 Обозначение

3 Процесс прямого распространения

Чтобы продемонстрировать, как находить выход, имея уже известный вход, в нейронных сетях, начнем с предыдущего примера с тремя слоями. Ниже такая система представлена в виде системы уравнений:

3.1 Пример прямого распространения

Представим эту матрицу через массивы библиотеки numpy.

Мы просто присвоили некоторые рандомные числовые значения весу каждой связи с Ш1. Аналогично можно сделать и с Ш2:

Мы можем присвоить некоторые значения весу смещения в Ш1 и Ш2:

Наконец, перед написанием основной программы для расчета выхода нейронной сети, напишем отдельную функцию для активационной функции:

3.2 Первая попытка реализовать процесс прямого распространения

Приведем простой способ расчета выхода нейронной сети, используя вложенные циклы в Python. Позже мы быстро рассмотрим более эффективные способы.

Функция сначала проверяет, чем является входной массив для соответствующего слоя с узлами / весами. Если рассматривается первый слой, то входом для второго слоя является входной массив xx, Умноженный на соответствующие веса. Если слой не первый, то входом для последующего будет выход предыдущего.
Вызов функции:

возвращает результат 0.8354. Можно проверить правильность, вставив те же значения в систему уравнений:

3.3 Более эффективная реализация

В данном случае процесс прямого распространения с циклами занимает около 40 микросекунд. Это довольно быстро, но не для больших нейронных сетей с > 100 узлами на каждом слое, особенно при их обучении. Если мы запустим этот алгоритм на нейронной сети с четырьмя слоями, то получим результат 70 микросекунд. Эта разница является достаточно значительной.

3.4 Векторизация в нейронных сетях

, где n- количество узлов в Ш1. Используя это обозначение, систему уравнений можно сократить:

Обратите внимание на W, что означает матричную форму представления весов. Помните, что теперь все элементы в уравнении сверху являются матрицами / векторами. Но на этом упрощение не заканчивается. Данные уравнения можно свести к еще более краткому виду:

3.5 Умножение матриц

Распишем z (l+1) =W (l) h (l) +b (l) на выражение из матрицы и векторов входного слоя ( h (l) =x):

Для тех, кто не знает или забыл, как перемножаются матрицы. Когда матрица весов умножается на вектор, каждый элемент в строке матрицы весов умножается на каждый элемент в столбце вектора, после этого все произведения суммируются и создается новый вектор (3х1). После перемножения матрицы на вектор, добавляются элементы из вектора смещения и получается конечный результат.

Каждая строка полученного вектора соответствует аргументу активационной функции в оригинальной НЕ матричной системе уравнений выше. Это означает, что в Python мы можем реализовать все, не используя медленные циклы. К счастью, библиотека numpy дает возможность сделать это достаточно быстро, благодаря функциям-операторам над матрицами. Рассмотрим код простой и быстрой версии функции simple_looped_nn_calc:

Обратите внимание на строку 7, в которой происходит перемножение матрицы и вектора. Если вместо функции умножения a.dot (b) вы используете символ *, то получится нечто похожее на поэлементное умножение вместо настоящего произведения матриц.

Если сравнить время работы этой функции с предыдущей на простой сети с четырьмя слоями, то мы получим результат лишь на 24 микросекунды меньше. Но если увеличить количество узлов в каждом слое до 100-100-50-10, то мы получим гораздо большую разницу. Функция с циклами в этом случае дает результат 41 миллисекунду, когда у функции с векторизацией это занимает лишь 84 микросекунды. Также существуют еще более эффективные реализации операций над матрицами, которые используют пакеты глубинного обучения, такие как TensorFlow и Theano.

На этом все о процессе прямого распространения в нейронных сетях. В следующих разделах мы поговорим о способах обучения нейронных сетей, используя градиентный спуск и обратное распространение.

4 Градиентный спуск и оптимизация

Расчеты значений весов, которые соединяют слои в сети, это как раз то, что мы называем обучением системы. В контролируемом обучении идея заключается в том, чтобы уменьшить погрешность между входом и нужным выходом. Если у нас есть нейросеть с одним выходным слоем и некоторой вход xx и мы хотим, чтобы на выходе было число 2, но сеть выдает 5, то нахождение погрешности выглядит как abs(2-5)=3. Говоря языком математики, мы нашли норму ошибки L 1 (Это будет рассмотрено позже).

y (1) в этом случае может представлять собой единое скалярное значение, например, 1 или 0, обозначающий, было сообщение спамом или нет. В других приложениях это также может быть вектор с K измерениями. Например, мы имеем вход xx, Который является вектором черно-белых пикселей, считанных с фотографии. При этом y может быть вектором с 26 элементами со значениями 1 или 0, обозначающие, какая буква была изображена на фото, например (1,0. 0)для буквы а, (0,1. 0) для буквы б и т. д.

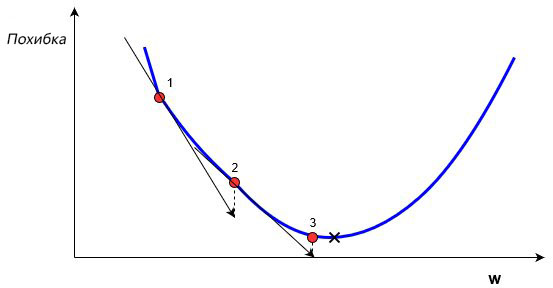
В обучении сети, используя (x,y), целью является улучшение нахождения правильного y при известном x. Это делается через изменение значений весов, чтобы минимизировать погрешность. Как тогда менять их значение? Для этого нам и понадобится градиентный спуск. Рассмотрим следующий график:

На этом графике изображено погрешность, зависящую от скалярного значения веса, w. Минимально возможная погрешность обозначена черным крестиком, но мы не знаем какое именно значение w дает нам это минимальное значение. Подсчет начинается с рандомного значения переменной w, которая дает погрешность, обозначенную красной точкой под номером «1» на кривой. Нам нужно изменить w таким образом, чтобы достичь минимальной погрешности, черного крестика. Одним из самых распространенных способов является градиентный спуск.

Метод градиентного спуска использует градиент, чтобы принимать решение о следующей смены в w для того, чтобы достичь минимального значения кривой. Он итеративным методом, каждый раз обновляет значение w через:

, где w_н означает новое значение w, w_ст— текущее или «старое» значение w, ∇error является градиентом погрешности на w_ст и α является шагом. Шаг α также будет означать, как быстро ответ приближается к минимальной погрешности. При каждой итерации в таком алгоритме градиент должен уменьшаться. Из графика выше можно заметить, что с каждым шагом градиент «стихает». Как только ответ достигнет минимального значения, мы уходим из итеративного процесса. Выход можно реализовать способом условия «если погрешность меньше некоторого числа». Это число называют точностью.

4.1 Простой пример на коде

Мы будем находить градиент нейронной сети, используя достаточно популярный метод обратного распространения ошибки, о котором будет написано позже. Но сначала нам нужно рассмотреть функцию погрешности более детально.

4.2 Функция оценки

Выражение является функцией оценки учебного экземпляра z_th, где h (nl) является выходом последнего слоя, то есть выход нейронной сети. h (nl) можно представить как yпyп, Что означает полученный результат, когда нам известен вход xz. Две вертикальные линии означают норму L 2 погрешности или сумму квадратов ошибок. Сумма квадратов погрешностей является довольно распространенным способом представления погрешностей в системе машинного обучения. Вместо того, чтобы брать абсолютную погрешность abs(ypred(x z )-y z ), мы берем квадрат погрешности. Мы не будем обсуждать причину этого в данной статье. 1/2 в начале просто константой, которая нормализует ответ после того, как мы продифференцируем функцию оценки во время обратного распространения.

Обратите внимание, что приведенная ранее функция оценки работает только с одной парой (x,y). Мы хотим минимизировать функцию оценки со всеми mm парами вход-выход:

Тогда как же мы будем использовать функцию J для обучения наших сетей? Конечно, используя градиентный спуск и обратное распространение ошибок. Сначала рассмотрим градиентный спуск в нейронных сетях более детально.

4.3 Градиентный спуск в нейронных сетях

Градиентный спуск для каждого веса w_(ij) (l) и смещение bi(l) в нейронной сети выглядит следующим образом:

Значения ∂/∂w_ij (l) и ∂/∂b_i (l) являются частными производными функции оценки, основываясь на значениях веса. Что это значит? Вспомните простой пример градиентного спуска ранее, каждый шаг зависит от наклона погрешности / оценки по отношению к весу. Производная также имеет значение наклона / градиента. Конечно, производная обозначается как d/dx. x в нашем случае является вектором, а это значит, что наша производная тоже будет вектором, который является градиент каждого измерения x.

4.4 Пример двумерного градиентного спуска

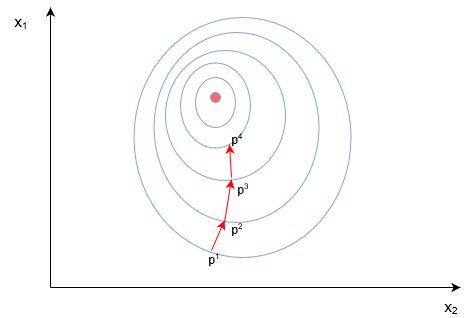
Рассмотрим пример стандартного двумерного градиентного спуска. Ниже представлены диаграмму работы двух итеративных двумерных градиентных спусков:

Синим обозначены контуры функции оценки, они обозначают области, в которых значение погрешности примерно одинаковы. Каждый шаг (p1→p2→p3) В градиентном спуске используют градиент или производную, которые обозначаются стрелкой / вектором. Этот вектор проходит через два пространства [x1, x2][x1,x2]и показывает направление, в котором находится минимум. Например, производная, исчисленная в p1 может быть d/dx=[2.1,0.7], Где производная является вектором с двумя значениями. Частичная производная ∂/∂x₁ в этом случае равна скаляру →[2.1]- иными словами, это значение градиента только в одном измерении поискового пространства (x1).

Поэтому нам нужен метод обратного распространения. Этот метод дает нам возможность «делить» функцию оценки или ошибку со всеми весами в сети. Другими словами, мы можем выяснить, как каждый вес влияет на погрешность.

4.5 Углубляемся в обратное распространение

Если математика вам не очень хорошо дается, то вы можете пропустить этот раздел. В следующем разделе вы узнаете, как реализовать обратное распространение языке программирования. Но если вы не против немного больше поговорить о математике, то продолжайте читать, вы получите более глубокие знания по обучению нейронных сетей.

Сначала, давайте вспомним базовые уравнения для нейронной сети с тремя слоями из предыдущих разделов:

Выход этой нейронной сети находится по формуле:

Если присмотреться, то правая часть полностью сокращается (по принципу 2552=22=1). ∂J∂w12(2) были разбиты на три множителя, два из которых можно прекрасно заменить. Начнем с ∂z₁ (2) /∂w₁₂ (2) :

здесь y1 является ожидаемым выходом для выходного узла. Опять используем правило дифференцирования сложной функции:

Мы выяснили, как находить ∂J/∂w₁₂ (2) по крайней мере для весов связей с исходным слоем. Перед тем, как перейти к одному из скрытых слоев, введем некоторые новые значения δ, чтобы немного сократить наши выражения:

, где i является номером узла в выходном слое. В нашем примере есть только один узел, поэтому i=1. Напишем полный вид производной функции оценки:

, где выходной слой, в нашем случае, l=2, а i соответствует номеру узла.

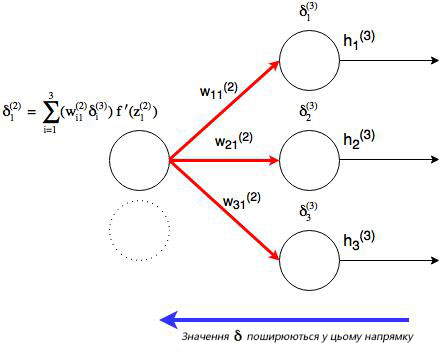
4.6 Распространение в скрытых слоях

Что делать с весами в скрытых слоях (в нашем случае в слое 2)? Для весов, которые соединены с выходным слоем, производная ∂J/∂h=-(y_i-h_i (nl) )имела смысл, т.к. функция оценки может быть сразу найдена через сравнение выходного слоя с существующими данными. Но выходы скрытых узлов не имеют подобных уже существующих данных для проверки, они связаны с функцией оценки только через другие слои узлов. Как мы можем найти изменения в функции оценки из-за изменений весов, которые находятся глубоко в нейронной сети? Как уже было сказано, мы используем метод обратного распространения.

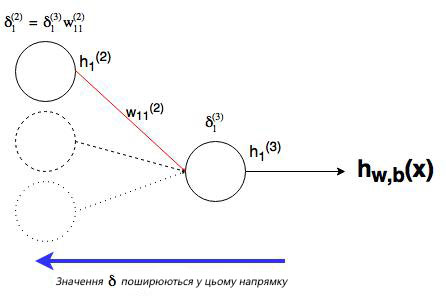
Как можно понять из рисунка, выходной слой соединяется со скрытым узлом из-за веса. В случае, когда в исходном слое есть только один узел, общее выражение скрытого слоя будет выглядеть так:

, где j номер узла в слое l. Но что будет, если в исходном слое находится много выходных узлов? В этом случае δ_j (l) находится по взвешенной сумме всех связанных между собой погрешностей, как показано на диаграмме ниже:

Отлично, теперь мы знаем, как реализовать градиентный спуск в нейронных сетях:

Однако, для такой реализации, нам нужно будет снова применить циклы. Как мы уже знаем из предыдущих разделов, циклы в языке программирования Python работают довольно медленно. Нам нужно будет понять, как можно векторизовать такие подсчеты.

4.7 Векторизация обратного распространения

Для того, чтобы понять, как векторизовать процесс градиентного спуска в нейронных сетях, рассмотрим сначала упрощенную векторизованную версию градиента функции оценки (внимание: это пока неправильная версия!):

Используя операцию трансформирования, мы можем достичь результата, который нам нужен.

Еще одно трансформирование нужно сделать с суммой погрешностей в обратном распространении:

символ (∙) в предыдущем выражении означает поэлементное умножение (произведение Адамара), не является умножением матриц. Обратите внимание, что произведение матриц (((W (l) ) T δ_(l+1))требует еще одного сложения весов и значений δ.

4.8 Реализация этапа градиентного спуска

Как тогда интегрировать векторизацию в этапы градиентного спуска нашего алгоритма? Во-первых, вспомним полный вид нашей функции оценки, который нам нужно сократить:

Из формулы видно, что полная функция оценки состоит из суммы поэтапных расчетов функции оценки. Также следует вспомнить, как находится градиентный спуск (поэлементная и векторизованная версии):

4.9 Конечный алгоритм градиентного спуска

Из этого алгоритма следует, что мы будем повторять градиентный спуск, пока функция оценки не достигнет минимума. На этом этапе нейросеть считается обученной и готовой к использованию.

Далее мы попробуем реализовать этот алгоритм на языке программирования для обучения нейронной сети распознаванию чисел, написанных от руки.

5 Имплементация нейросети языке Python

Код, который мы собираемся написать в нашей нейронной сети, будет анализировать цифры, которые изображают пиксели на изображении. Для начала, нам нужно отсортировать входные данные. Для этого мы сделаем две следующие вещи:

01. Масштабировать данные.
02. Разделить данные на тесты и учебные тесты.

5.1 Масштабирование данных

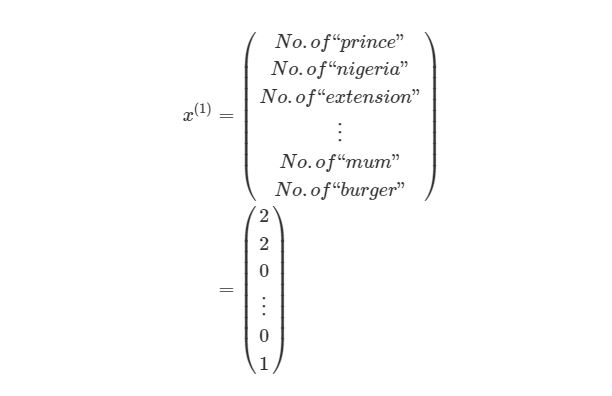
Почему нам нужно масштабировать данные? Во-первых, рассмотрим представление пикселей одного из сетов данных:

Заметили ли вы, что входные данные меняются в интервале от 0 до 15? Достаточно распространенной практикой является масштабирование входных данных так, чтобы они были только в интервале от [0, 1], или [1, 1]. Это делается для более легкого сравнения различных типов данных в нейронной сети. Масштабирование данных можно легко сделать через библиотеку машинного обучения scikit learn:

5.2 Создание тестов и учебных наборов данных

Опять же, scikit learn легко разбивает данные на учебные и тестовые наборы:

5.3 Настройка выходного слоя

В данных MNIST нужны результаты от изображений записаны как отдельное число. Нам нужно конвертировать это единственное число в вектор, чтобы его можно было сравнивать с исходным слоем с 10 узлами. Иными словами, если результат в MNIST обозначается как «1», то нам нужно его конвертировать в вектор: [0, 1, 0, 0, 0, 0, 0, 0, 0, 0]. Такую конвертацию осуществляет следующий код:

Этот код конвертирует «1» в вектор [0, 1, 0, 0, 0, 0, 0, 0, 0, 0].

5.4 Создаем нейросеть

Мы снова используем сигмоидальную активационную функцию, так что сначала нужно объявить эту функцию и ее производную:

Сейчас мы не имеем никакого представления, как выглядит наша нейросеть. Как мы будем ее учить? Вспомним наш алгоритм из предыдущих разделов:
Рандомно инициализируем веса для каждого слоя W (l) Когда итерация (l) б. Найдите значение δ ( nl) выходного слоя. Обновите ΔW (l) и Δb ( l ) для каждого слоя.
03. Запустите процесс градиентного спуска, используя:

Значит первым этапом является инициализация весов для каждого слоя. Для этого мы используем словари в языке программирования Python (обозначается через <>). Рандомные значения предоставляются весам для того, чтобы убедиться, что нейросеть будет работать правильно во время обучения. Для рандомизации мы используем random_sample из библиотеки numpy. Код выглядит следующим образом:

Следующим шагом является присвоение двум переменным ΔW и Δb нулевых начальных значений (они должны иметь такой же размер, что и матрицы весов и смещений)

Далее запустим процесс прямого распространения через нейронную сеть:

И наконец, найдем выходной слой δ (nl) и значение δ (l) в скрытых слоях для запуска обратного распространения:

Теперь мы можем соединить все этапы в одну функцию:

И наконец, после того, как мы прошлись по всем учебным экземплярам, накапливая значение tri_W и tri_b, мы запускаем градиентный спуск и меняем значения весов и смещений:

После окончания процесса, мы возвращаем полученные вес и смещение со средней оценкой для каждой итерации. Теперь время вызвать функцию. Ее работа может занять несколько минут, в зависимости от компьютера.

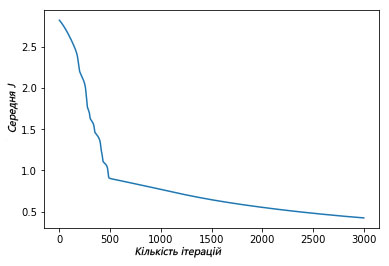
Мы можем увидеть, как функция средней оценки уменьшилась после итерационной работы градиентного спуска:

Выше изображен график, где показано, как за 3000 итераций нашего градиентного спуска функция средней оценки снизилась и маловероятно, что подобная итерация изменит результат.

5.5 Оценка точности модели

Теперь, наконец, мы можем оценить точность результата (процент раз, когда сеть выдала правильный результат), используя функцию accuracy_score из библиотеки scikit learn:

Мы получили результат 86% точности. Звучит довольно неплохо? На самом деле, нет, это довольно низкая точностью. В наше время точность алгоритмов глубинного обучения достигает 99.7%, мы немного отстали.

Источник