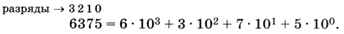что такое вес позиции в системе счисления
Содержание урока
§9. Системы счисления
§10. Позиционные системы счисления
Основные понятия
§11. Двоичная система счисления
§10. Позиционные системы счисления
Основные понятия
Позиционная система счисления — это такая система счисления, в которой значение цифры («вес») полностью определяется её местом (позицией) в записи числа.
Пример позиционной системы счисления — привычная нам десятичная система. В числе 6375 цифра 6 обозначает тысячи (т. е. 6000), цифра 3 — сотни (300), цифра 7 — десятки (70), а цифра 5 — единицы:
6375 = 6 • 1000 + 3 • 100 + 7 • 10 + 5 • 1.
Алфавит системы счисления — это используемый в ней набор цифр.
Основание системы счисления — это количество цифр в алфавите (мощность алфавита).
В десятичной системе основание — 10, алфавит состоит из 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Число 10, вероятно, было выбрано потому, что люди сначала использовали для счета свои 10 пальцев на руках.
Разряд — это позиция цифры в записи числа. Разряды в записи целых чисел нумеруются с нуля справа налево.
В числе 6375 цифра 6 стоит в третьем разряде (тысячи, 10 3 ), 3 — во втором разряде (сотни, 10 2 ), 7 — в первом (десятки, 10 1 ), а 5 — в нулевом (единицы, 10 0 ). Не забывайте, что любое число (кроме нуля!) в нулевой степени равно 1. Поэтому
Это так называемая развёрнутая форма записи числа. Из этой записи видно, что последняя цифра 5 — это остаток от деления числа на 10 (все остальные слагаемые делятся на 10); число, составленное из двух последних цифр (75), — это остаток от деления исходного числа на 100 = 10 2 и т. д. Поэтому все числа, делящиеся на 100 без остатка, оканчиваются на два нуля.
Чтобы определить число, записанное в позиционной системе счисления, нужно значение каждой цифры умножить на основание системы счисления в степени, равной разряду этой цифры, и сложить полученные величины.
Число 6375 можно представить в другой форме — по схеме Горнера:
6375 = ((6 • 10 + 3) • 10 + 7) • 10 + 5.
Эта форма позволяет найти число, используя только умножение и деление (без возведения в степень).
Кроме десятичной системы на практике используются ещё несколько позиционных систем:
• двоичная, восьмеричная и шестнадцатеричная в компьютерной технике;
• двенадцатеричная английская система мер (1 фут =12 дюймов, 1 шиллинг = 12 пенсов);
• шестидесятеричная система измерения времени (1 час = = 60 минут, 1 минута = 60 секунд).
Следующая страница 
Целые числа
Cкачать материалы урока
Системы счисления. Основные понятия.
Запись числа в некоторой системе счисления называется кодом числа.
Количество разрядов в записи числа называют разрядностью и совпадает с его длиной.
Системы счисления делятся на позиционные и непозиционные. Позиционные системы счисления делятся
на однородные и смешанные.
Непозиционная система счисления — древнейшая, здесь все цифры числа имеют величину, которая не
зависит от позиции (разряда).
Т.е., если есть 5 палочек, значит число соответственно равно 5, так как каждой палочке, вне зависимости
от её места в строке, соответствует только 1 предмет.
Позиционная система счисления — значение каждой цифры зависит от позиции (разряда) этой цифры в числе.
Например, стандартная 10-я система счисления является позиционной. Допустим дано число 453.
Цифра 4 означает число сотен и соответствует числу 400, 5 — кол-во десятков и соответствует значению
50, а 3 — единицы и значению 3. Легко заметить, что с увеличением разряда увеличивается значение.
Таким образом, заданное число запишем в виде суммы 400+50+3=453.
Однородная система — для каждого разряда (позиции) числа набор допустимых символов (цифр)
одинаковый. Как пример снова используем 10-ю систему. Если записывать число в однородной 10-й системе,
(1-й разряд — 0, 2-й — 5, 3-й — 4), а 4F5 — нет, так как символ F не входит в набор цифр от 0 до 9.
Смешанная система — в каждом разряде (позиции) числа набор допустимых символов (цифр) может
отличаться от наборов в других разрядах. Хороший пример — система измерения времени. В разряде
В непозиционных системах счисления вес цифры не зависим от позиции, которую она занимает в
числе. К примеру, в римской системе счисления в числе XXXII (32) вес цифры X в каждой позиции
Цифрами в римской системе служат: I(1), V(5), X(10), L(50), C(100), D(500), M(1000).
Размер числа в римской системе счисления определяют как сумму либо разность цифр в числе. Когда
меньшая цифра стоит слева от большей – она вычитается, когда справа – прибавляется.
Самая первая система счисления — единичная (непозиционная).
В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее позиции в
последовательности цифр, которые изображают число.
Каждая позиционная система характеризуется своим основанием.
Основание позиционной системы счисления – это количество разных знаков либо символов, которые
используются для изображения цифр в этой системе.
множество позиционных систем.
Перевод систем счисления. Числа можно перевести из одной системы счисления в другую.
Таблица соответствия цифр в различных системах счисления.