что такое в противоположных направлениях
в противоположном направлении
Смотреть что такое «в противоположном направлении» в других словарях:
вращающий момент в противоположном направлении — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN backward torque … Справочник технического переводчика
наклон в направлении, противоположном региональному — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN critical dip … Справочник технического переводчика
Корреляция — (Correlation) Корреляция это статистическая взаимосвязь двух или нескольких случайных величин Понятие корреляции, виды корреляции, коэффициент корреляции, корреляционный анализ, корреляция цен, корреляция валютных пар на Форекс Содержание… … Энциклопедия инвестора
Ретроградное движение — Эта статья о обратном движении небесных тел относительно центрального объекта. О видимом обратном движении по небесной сфере (попятном движении) см. Движение Солнца и планет по небесной сфере. Ре … Википедия
ПРОНИЦАЕМОСТЬ — ПРОНИЦАЕМОСТЬ, способность перегородки или мембраны пропускать растворенные вещества. Если мембрана, пропуская одни вещества, задерживает другие, она называется полупроницаемой. Обычно полупроницаемые мембраны пропускают растворитель (напр. воду) … Большая медицинская энциклопедия
Каги (график) — График Каги для котировок евро за доллар США в октябре 2009 года. Параметр разворота = 20 пунктов … Википедия
Игра против рынка — (Trading against the trend) Игра против рынка это ожидание значительного движения цены и затем открытие позиции в противоположном направлении Определение и понятие игры против рынка, методы и стратегии торговли против тренда, и крупные инвесторы … Энциклопедия инвестора
Балансировка двигателя — Стиль этой статьи неэнциклопедичен или нарушает нормы русского языка. Статью следует исправить согласно стилистическим правилам Википедии. У этого термина существуют и другие значения, см. Балансировка. Балансировка двигателя операция,… … Википедия
ГОСТ Р 53636-2009: Целлюлоза, бумага, картон. Термины и определения — Терминология ГОСТ Р 53636 2009: Целлюлоза, бумага, картон. Термины и определения оригинал документа: 3.4.49 абсолютно сухая масса: Масса бумаги, картона или целлюлозы после высушивания при температуре (105 ± 2) °С до постоянной массы в условиях,… … Словарь-справочник терминов нормативно-технической документации
Задачи на движение в противоположных направлениях
Урок 32. Решение текстовых задач по математике 1-4 классы
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Задачи на движение в противоположных направлениях»
А давайте с вами заглянем в семью Прошкиных и посмотрим, что у них происходит.
Этого мальчика зовут Денис. Это дедушка Дениса. Интересно, а почему Денис так странно себя ведёт?
– Денис, что случилось? Ты чего ходишь туда сюда?
– Понимаешь, дедушка. Мне в классе нравится одна девочка, Аня. И она попросила, чтобы я научил её решать задачи на движение в противоположных направлениях. А как я могу её научить, если я сам не умею решать такие задачи?
– Как тебе повезло, что у тебя такой умный дедушка. Я, между прочим, увлекаюсь решением задач по математике. Так что своего внука я легко смогу научить решать такие задачи.
Итак, слушай внимательно первую задачу.
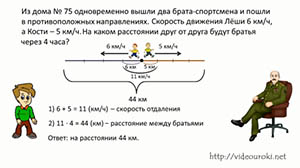
Из дома № 75 одновременно вышли два брата-спортсмена и пошли в противоположных направлениях. Скорость движения Лёши 6 км/ч, а Кости – 5 км/ч. На каком расстоянии друг от друга будут братья через 4 часа?
Обрати внимание на слова «в противоположных направлениях». Эти слова говорят о том, что задача на движение в противоположных направлениях.
Давай выполним рисунок к этой задаче.
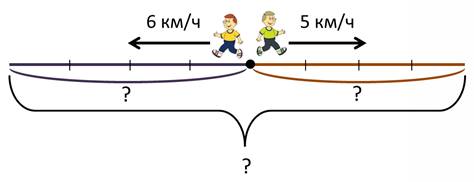
Точкой обозначим дом, из которого вышли братья, стрелочками укажем направление их движения, а так же укажем скорость их движения.
Чтобы найти расстояние, на котором будут братья через 4 часа, надо знать расстояние, которое пройдёт каждый из них за это время. А ты знаешь, как найти расстояние?
– Знаю, чтобы найти расстояние надо скорость умножить на время.
– Молодец. Правильно. Нам известны скорость, с которой двигался Лёша – 6 км/ч, и время, которое он находился в пути – 4 часа. Значит, мы можем найти расстояние, пройденное Лёшей? Так как мы его найдём?
– Надо его скорость 6 км/ч, умножить на время 4 часа. Получается 24 км прошёл Лёша.
И точно так же мы можем узнать, сколько прошёл его брат, Костя. Его скорость 5 км/ч умножим на время в пути 4 ч. Получается Костя прошёл 20 км.
Ну, узнали мы, сколько прошёл Лёша и Костя, а дальше что?
– А теперь, когда мы знаем, сколько прошёл каждый из братьев отдельно, можем узнать, расстояние между ними.
Ответ: через 4 часа братья будут друг от друга на расстояние 44 километра.
– Ну, мне всё понятно. Я пошёл к Ане, объяснять решение таких задач.
– Подожди. Не торопись. Эту задачу можно решить и другим способом. Вернёмся к нашему рисунку.
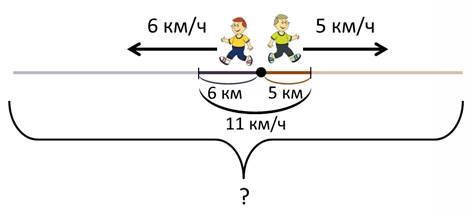
Смотри, за один час Лёша отдалился от дома на 6 км, за этот же час Костя отдалился на 5 км. И за это время они отдалились друг от друга на расстояние, равное сумме этих двух чисел. Только это не расстояние. Ведь отдалились они друг от друга за 1 час. Значит, – это скорость их удаления, а точнее, «скорость отдаления» друг от друга.
1) 6 + 5 = 11 (км/ч) – скорость отдаления братьев друг от друга за 1 час
– Ага, если мы знаем, на сколько километров они отдалились друг от друга за 1 час, значит, на сколько они отдалились друг от друга за 4 часа, можно узнать… м–м–м. действием умножения.
Ответ: через 4 часа братья будут друг от друга на расстояние 44 километра.
Я надеюсь, ещё одного способа решения таких задач нет? И я уже могу идти?
– Способов больше нет…. Но я считаю, что учить других ты ещё не готов. Знаешь такую поговорку «Поспешишь – людей насмешишь». Вот попробуй решить такую задачу.
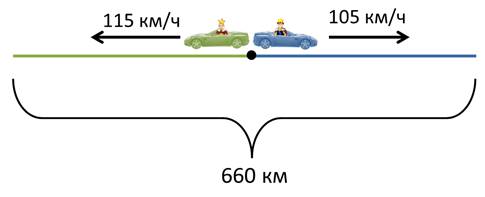
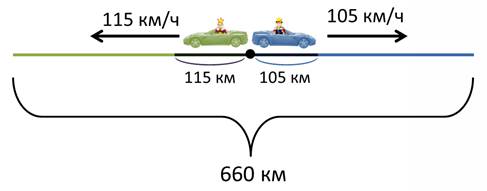
Из центра города Н выехали одновременно в противоположных направлениях король Луи и король Вилли. Средняя скорость автомобиля короля Луи 105 км/ч, а автомобиля короля Вилли – 115 км/ч. Через сколько часов расстояние между королями будет 660 км.
– Что-то я тут опять ничего не понимаю.
– Давай разбираться. Изобразим всё на рисунке.
Точкой обозначим центр города, укажем направление движения и скорости автомобилей королей. Ещё мы знаем, то через некоторое время расстояние между королями будет 660 км. И это время нам надо найти.
– Та-а-ак, наверное, сначала надо всё расстояние разделить на скорость каждого автомобиля.
1) 660 : 115 = ….м–м–м не длится. А-а-а, наверное, надо умножить….
– Подожди, не торопись. Ты сначала хорошо подумай. Обрати внимание на то, что 660 км – это расстояние, которое проехали два автомобиля вместе, а ты собираешься делить по отдельности на скорость первого короля и второго. Если расстояние совместно пройдено, то и скорость должна быть совместная.
Для того чтобы найти время, надо знать расстояние и скорость обоих автомобилей вместе. Мы знаем, что за каждый час один автомобиль отдаляется от города на 105 км, а второй за этого же время – на 115 км. Т.е. они отдаляются за каждый час друг от друга на сумму этих расстояний.
1) 105 + 115 = 220 (км/ч) – скорость отдаления
А раз мы знаем скорость отдаления и всё расстояние пройденное автомобилями, то именно теперь мы можем найти их время в пути. Для этого надо расстояние разделить на скорость отдаления.
2) 660 : 220 = 3 (часа)
Ответ: через 3 часа расстояние между королями будет 660 км.
– А–а–а, теперь я понял свою ошибку. Сначала надо было найти скорость отдаления обоих королей, а затем уже расстояние делить на скорость отдаления.
– Ну, раз ты понял свою ошибку, тогда слушай ещё одну задачу.
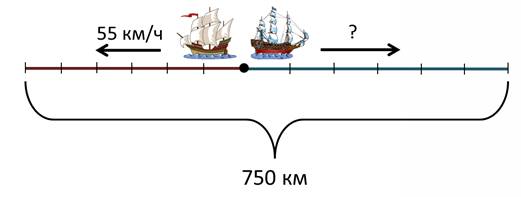
От острова одновременно отплыли два корабля в противоположных направлениях. Через 6 часов расстояние между ними было 750 километров. Первый корабль плыл со скоростью 55 км/ч. С какой скоростью плыл второй корабль?
– Да-а-а, интересная задача. Можно я сам попробую её решить.
Я понял, что лучше начать с рисунка – так нагляднее.
Точкой обозначим остров, стрелочками укажем направление движения кораблей. За 6 часов они проплыли 750 километров…
Скорость одного корабля 55 км/ч, а скорость второго корабля мне предстоит узнать.
Та-а-а-ак, чтобы найти скорость второго корабля, надо знать расстояние, которое он проплыл и время, которое он был в пути. Но, мы не знаем, какое расстояние проплыл второй корабль. Нам надо его найти. А как нам его найти? А-а-а. Нам надо знать общее расстояние, и какое расстояние проплыл первый корабль. Общее расстояние мы знаем, а расстояние, которое проплыл первый корабль, мы узнаем, умножив его скорость на время в пути.
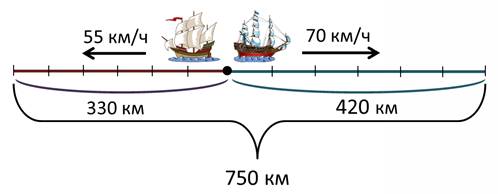
1) 55 · 6 = 330 (км) – проплыл первый корабль за 6 часов
Мы знаем всё расстояние и ту его часть, которую проплыл первый корабль. И теперь мы можем узнать, какое расстояние проплыл второй корабль за 6 часов.
2) 750 – 330 = 420 (км) – проплыл второй корабль за 6 часов
Нам известно расстояние, которое проплыл второй корабль и время. Значит, мы легко можем узнать скорость второго корабля. Для этого надо расстояние разделить на время, которое он был в пути.
Ответ: скорость второго корабля 70 км/ч.
Ура! Ура! Я сам решил задачу на движение в противоположных направлениях.
– Ты молодец. Теперь я уверен, что ты готов к тому, чтобы учить других решать подобные задачи. Я горжусь своим внуком.
Задачи на движение в противоположных направлениях
Рассмотрим задачи, в которых речь идёт о движении в противоположных направлениях. В таких задачах два каких-нибудь объекта движутся в противоположных направлениях, отдаляясь друг от друга. Задачи на движение в противоположных направлениях можно решать двумя способами.
Задача 1. Два автомобиля выехали одновременно из одного и того же пункта в противоположных направлениях. Скорость первого автомобиля 100 км/ч, скорость второго — 70 км/ч. Какое расстояние будет между автомобилями через 4 часа?
Решение: Из условия задачи известны скорость каждого автомобиля и время, которое автомобили были в пути. Значит, можно найти расстояние, которое проехал каждый автомобиль, для этого нужно скорость умножить на время:
1) 100 · 4 = 400 (км) — проехал первый автомобиль,
2) 70 · 4 = 280 (км) — проехал второй автомобиль.
Найдя сумму полученных результатов, узнаем расстояние между автомобилями через 4 часа:
Данную задачу можно решить и другим способом. Каждый час расстояние между автомобилями увеличивалось на 170 километров (100 + 70), 170 км/ч — это скорость удаления автомобилей. За 4 часа они проедут расстояние:
Таким образом, задачу на движение в противоположных направлениях можно решить двумя способами:
| 1-й способ: | 2-й способ: |
|---|---|
| 1) 100 · 4 = 400 (км) | 1) 100 + 70 = 170 (км/ч) |
| 2) 70 · 4 = 280 (км) | 2) 170 · 4 = 680 (км) |
| 3) 400 + 280 = 680 (км) |
Ответ: Через 4 часа между автомобилями будет 680 км.
Задача 2. Из двух населённых пунктов, расстояние между которыми 40 км, вышли в противоположных направлениях два пешехода. Первый пешеход шёл со скоростью 4 км/ч, а второй — 5 км/ч. Какое расстояние между пешеходами будет через 5 часов?
Решение: Сначала можно определить сколько километров прошёл каждый из пешеходов за 5 часов, для этого скорость пешеходов умножим на 5:
1) 4 · 5 = 20 (км) — прошёл первый пешеход,
2) 5 · 5 = 25 (км) — прошёл второй пешеход.
Затем можно найти общий путь, пройденный двумя пешеходами за 5 часов:
Теперь можно найти расстояние между пешеходами, прибавив к пути, пройденному пешеходами, расстояние между населёнными пунктами:
У данной задачи есть и второй вариант решения. Можно сначала найти скорость удаления пешеходов:
Затем найти пройденное расстояние, умножив скорость удаления (9 км/ч) на время движения пешеходов (5 ч):
А теперь, для нахождения расстояния между пешеходами, сложить пройденное расстояние (45 км) с расстоянием между населёнными пунктами:
Таким образом, данная задача имеет два варианта решения:
| 1-й способ: | 2-й способ: |
|---|---|
| 1) 4 · 5 = 20 (км) | 1) 4 + 5 = 9 (км/ч) |
| 2) 5 · 5 = 25 (км) | 2) 9 · 5 = 45 (км) |
| 3) 20 + 25 = 45 (км) | 3) 45 + 40 = 85 (км) |
| 4) 45 + 40 = 85 (км) |
Ответ: Через 5 часов расстояние между пешеходами будет 85 км.
Задачи на движение

— простые задачи на скорость, время и расстояние;
— задачи на встречное и противоположное движение;
— задачи на движение в одном направлении (на сближение и удаление);
— решение задач на движение по реке.
Скорость, время и расстояние: определения, обозначения, формулы
скорость = расстояние: время — формула нахождения скорости;
время = расстояние: скорость — формула нахождения времени;
расстояние = скорость · время — формула нахождения расстояния.
Скорость – это расстояние, пройденное за единицу времени: за 1 секунду, за 1 минуту, за 1 час и так далее.
Пример обозначения: 7 км/ч (читается: семь километров в час).
Если весь путь проходится с одинаковой скоростью, то такое движение называется равномерным.
На сайте представлены калькуляторы онлайн, с помощью которых можно перевести скорость, время и расстояние в другие единицы измерения:
Примеры простых задач.
Задача 1.
Автомобиль проехал 180 км за 2 часа. Чему равна скорость автомобиля?
Решение: 180:2=90 (км/ч.)
Ответ: Скорость автомобиля равна 90 км/ч.
Задача 2.
Автобус проехал путь в 240 км со скоростью 80 км/ч. Сколько времени ехал автобус?
Решение: 240:80=3 (ч.)
Ответ: Автобус проехал 3 часа.
Задача 3.
Грузовик ехал 5 часов со скоростью 70 км/ч. Какое расстояние проехал грузовик за это время?
Решение: 70 · 3 = 350 (км)
Ответ: Грузовик за 5 часов проехал 350 км.
Задачи на встречное движение
В таких задачах два объекта движутся навстречу друг другу.
Задачи на встречное движение можно решать двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость сближения объектов (как сумму их скоростей), общие время и расстояние. Скорость сближения — это расстояние, пройденное двумя объектами навстречу друг другу за единицу времени.
Задача 4.
Из двух пунктов навстречу друг другу одновременно выехали два поезда и встретились через 3 часа. Первый поезд ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. На каком расстоянии друг от друга находятся пункты?
Решение:
Первый способ. Найти расстояние, которое проехал каждый автобус, и сложить полученные данные:
80*3=240 (км) – проехал 1й автобус, 70*3=210 (км) – проехал 2й поезд,
240+210=450 (км) – проехали два поезда.
Второй способ. Найти скорость сближения поездов, то есть на сколько сокращалось расстояние между ними каждый час; а затем найти расстояние:
80+70=150 (км/ч), 150*3=450 (км).
Ответ: города находятся на расстоянии 450 км.
Задача 5.
Из двух городов навстречу друг другу одновременно выехали два автобуса. Первый автобус ехал со скоростью 80 км/ч, а второй – со скоростью 70 км/ч. Какое расстояние будет между ними через 2 часа, если расстояние между городами 450 км?
Решение:
Первый способ. Определить, сколько километров проехал каждый автобус и найти расстояние, которое осталось проехать:
80*2=160 (км)-проехал 1й автобус, 70*2=140 (км)-проехал 2й автобус,
160+140=300 (км)-проехали два автобуса, 450-300=150 (км)-осталось проехать.
Второй способ. Найти скорость сближения автобусов и умножить ее на время в пути.
80*70=150 (км/ч) – скорость сближения; 150*2=300 (км) – проехали два автобуса; 450-300=150 (км) – осталось проехать.
Ответ: Через 2часа расстояние между автобусами будет 150 км.
Задачи на движение в противоположных направлениях
В таких задачах два объекта движутся в противоположных направлениях, отдаляясь друг от друга. В таком типе задачи используется скорость удаления. Задачи на движение в противоположных направлениях также можно решить двумя способами:
1. Найти значения скорости, времени и расстояния для каждого объекта.
2. Найти скорость удаления объектов (как сумму их скоростей), общие время и расстояние. Скорость удаления — это расстояние, которое увеличивается за единицу времени между двумя объектами, двигающимися в противоположных направлениях.
Задача 6.
Два автомобиля выехали одновременно из одного и того же пункта в противоположных направлениях. Скорость первого автомобиля 100 км/ч, скорость второго – 70 км/ч. Какое расстояние будет между автомобилями через 4 часа?
Решение:
Первый способ. Определить расстояние, которое проехал каждый автомобиль и найти сумму полученных результатов:
1) 100 · 4 = 400 (км) – проехал первый автомобиль
2) 70 · 4 = 280 (км) – проехал второй автомобиль
400 + 280 = 680 (км)
Второй способ. Найти скорость удаления, то есть значение увеличения расстояния между автомобилями за каждый час, а затем скорость удаления умножить на время в пути.
100 + 70= 170 км/ч – это скорость удаления автомобилей.
170 · 4 = 680 (км)
Ответ: Через 4 часа между автомобилями будет 680 км.
Задача 7.
Из двух населённых пунктов, расстояние между которыми 40 км, вышли в противоположных направлениях два туриста. Первый турист шёл со скоростью 4 км/ч, а второй — 5 км/ч. Какое расстояние между туристами будет через 5 часов?
Решение:
Первый способ. Определить сколько километров прошёл каждый из туристов за 5 часов, сложить полученные результаты, а затем к полученному расстоянию прибавить расстояние между населенными пунктами.
1) 4 · 5 = 20 (км) – прошёл первый турист;
2) 5 · 5 = 25 (км) – прошёл второй турист;
3) 20 + 25 = 45 (км);
4) 45 + 40 = 85 (км).
Второй способ. Найти скорость удаления пешеходов, затем найти пройденное расстояние, к полученному результату прибавить расстоянием между населёнными пунктами.
4 + 5 = 9 (км/ч);
9 · 5 = 45 (км);
45 + 40 = 85 (км);
Ответ: Через 5 часов расстояние между пешеходами будет 85 км.
Задачи на движение в одном направлении
В таких задачах два объекта движутся в одном направлении с разной скоростью, при этом они сближаются друг с другом или отдаляются друг от друга. Соответственно находится скорость сближения или скорость удаления объектов.
Формула нахождения скорости сближения или удаления двух объектов, которые движутся в одном направлении: из большей скорости вычесть меньшую.
Задача 8.
Из города выехал автомобиль со скоростью 40 км/ч. Через 4 часа вслед за ним выехал второй автомобиль со скоростью 60 км/ч. Через сколько часов второй автомобиль догонит первый?,
Решение:
Задачу можно решить с помощью уравнения.
В этом случае скорость первого автомобиля 40 км/час, время в пути на 4 часа больше, чем время второго автомобиля (или t+4). Скорость второго автомобиля 60 км/час, время в пути – t. Расстояние оба автомобиля проехали одинаковое. Поэтому можно составить уравнение: 40*(t+4)=60*t. Отсюда получаем t=8 (часов) – время в пути второго автомобиля, за которое он догонит первый.
Решение задачи без использования уравнения.
Так как на момент выезда второго автомобиля из города первый уже был в пути 4 часа, то за это время он успел удалиться от города на: 40 · 4 = 160 (км).
Второй автомобиль движется быстрее первого, значит, каждый час расстояние между автомобилями будет сокращаться на разность их скоростей: 60 — 40 = 20 (км/ч) – это скорость сближения.
Разделив расстояние между автомобилями на скорость их сближения, можно узнать, через сколько часов они встретятся: 160 : 20 = 8 (ч)
Ответ: Второй автомобиль догонит первый через 8 часов.
Задача 9.
Из двух посёлков между которыми 5 км, одновременно в одном направлении вышли два пешехода. Скорость пешехода, идущего впереди, 4 км/ч, а скорость пешехода, идущего позади 5 км/ч. Через сколько часов после выхода второй пешеход догонит первого?
Решение: Так как второй пешеход движется быстрее первого, то каждый час расстояние между ними будет сокращаться. Значит можно определить скорость сближения пешеходов: 5 — 4 = 1 (км/ч).
Оба пешехода вышли одновременно, значит расстояние между ними равно расстоянию между посёлками (5 км). Разделив расстояние между пешеходами на скорость их сближения, узнаем через сколько второй пешеход догонит первого: 5 : 1 = 5 (ч)
Ответ: Через 5 часов второй пешеход догонит первого.
Задача 10.
Два автомобиля выехали одновременно из одного и того же пункта в одном направлении. Скорость первого автомобиля 80 км/ч, а скорость второго – 40 км/ч.
1) Чему равна скорость удаления между автомобилями?
2) Какое расстояние будет между автомобилями через 3 часа?
3) Через сколько часов расстояние между ними будет 200 км?
Решение:
1) 80 — 40 = 40 (км/ч) — скорость удаления автомобилей друг от друга.
2) 40 · 3 = 120 (км) – расстояние между ними через 3 часа./
3) 200 : 40 = 5 (ч) – время, через которое расстояние между автомобилями станет 200 км.
Ответ:
1) Скорость удаления между автомобилями равна 40 км/ч.
2) Через 3 часа между автомобилями будет 120 км.
3) Через 5 часов между автомобилями будет расстояние в 200 км.
Задачи на движение по реке
Рассмотрим задачи, в которых речь идёт о движении объекта по реке. Скорость любого объекта в стоячей воде называют собственной скоростью этого объекта.
Чтобы узнать скорость объекта, который движется по течению реки, надо к собственной скорости объекта прибавить скорость течения реки. Чтобы узнать скорость объекта, который движется против течения реки, надо из собственной скорости объекта вычесть скорость течения реки.
Задача 11.
Лодка движется по реке. За сколько часов она преодолеет расстояние 120 км, если ее собственная скорость 27 км/ч, а скорость течения реки 3 км/ч?
Решение:
1) лодка движется по течению реки.
27 + 3 = 30 (км/ч) – скорость лодки по течению реки.
120 : 30 = 4 (ч) – проплывет путь.
2) лодка движется против течения реки.
27 — 3 = 24 (км/ч) — скорость лодки против течения реки
120 : 24 = 5 (ч) – проплывет путь.
Ответ:
1) При движении по течению реки лодка потратит 4 часа на путь.
2) При движении против течения реки лодка потратит 5 часов на путь.
Итак, для решения задач на движение:
Заключение.
Решая много задач по данной теме, ученик обязательно научится быстро ориентироваться в понятиях «скорость», «время» и «расстояние» и быстро решать задачи всех типов. Получить карточки с задачами разных видов можно по ссылке.