что такое свободные колебания в физике

Свободные колебания.

Свободные колебания (или собственные колебания) — это колебания колебательной системы, совершаемые только благодаря первоначально сообщенной энергии (потенциальной или кинети­ческой) при отсутствии внешних воздействий.

Потенциальная или кинетическая энергия может быть сообщена, например, в механических системах через начальное смещение или начальную скорость.

Свободно колеблющиеся тела всегда взаимодействуют с другими телами и вместе с ними обра­зуют систему тел, которая называется колебательной системой.

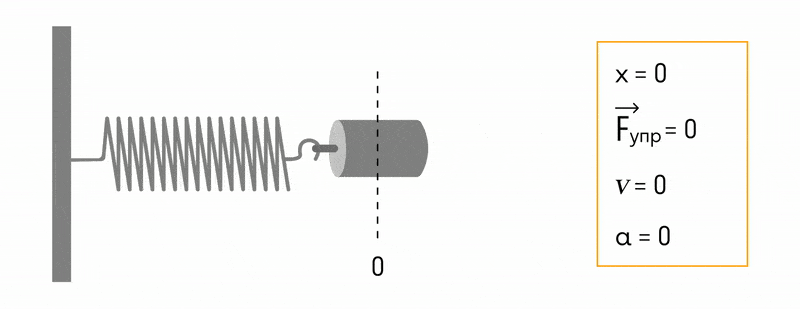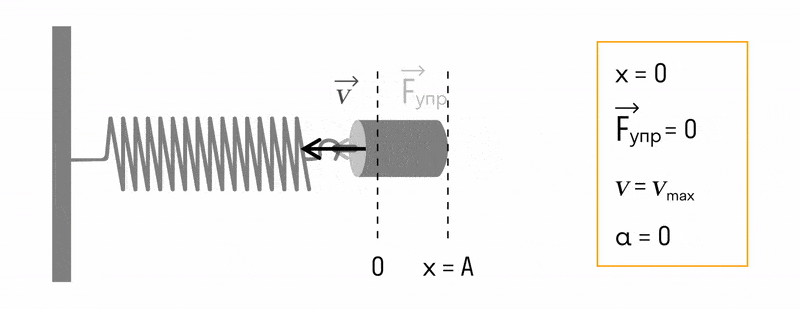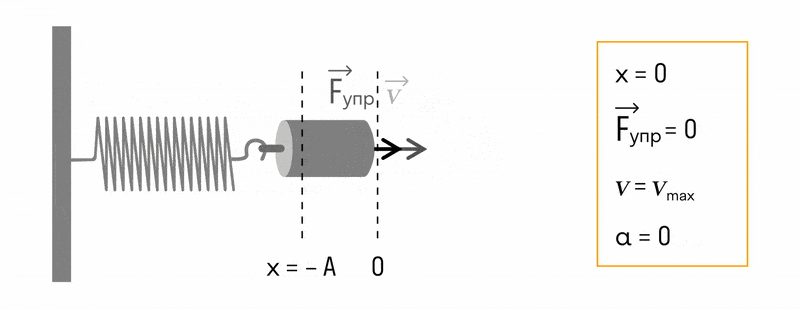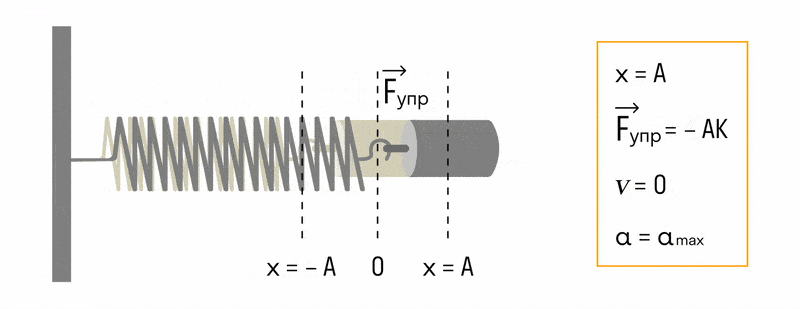
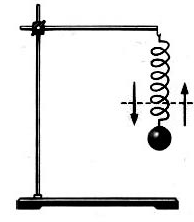
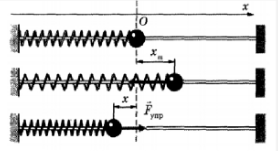
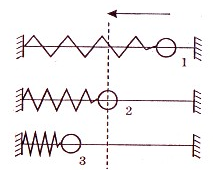
Например, пружина, шарик и вертикальная стойка, к которой прикреплен верхний конец пружины (см. рис. ниже), входят в колебательную систему. Здесь шарик свободно скользит по струне (силы трения пренебрежимо малы). Если отвести шарик вправо и предоставить его самому себе, он будет совершать свободные колебания около положения равновесия (точки О) вследствие действия силы упругости пружины, направленной к положению равновесия.

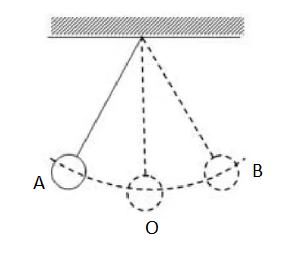
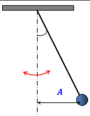
Другим классическим примером механической колебательной системы является математический маятник (см. рис. ниже). В данном случае шарик совершает свободные колебания под действием двух сил: силы тяжести и силы упругости нити (в колебательную систему входит также Земля). Их равнодействующая направлена к положению равновесия.

Силы, действующие между телами колебательной системы, называются внутренними силами. Внешними силами называют­ся силы, действующие на систему со стороны тел, не входящих в нее. С этой точки зрения свобод­ные колебания можно определить как колебания в системе под действием внутренних сил после того, как система выведена из положения равновесия.

Условиями возникновения свободных колебаний являются:

1) возникновение в них силы, возвращающей систему в положение устойчивого равновесия, после того как ее вывели из этого состояния;

2) отсутствие трения в системе.

Динамика свободных колебаний.

.

Это дифференциальное уравнение движения тела, колеблющегося под действием силы упругости: вторая производная координаты по времени (ускорение тела) прямо пропорциональна его координате, взятой с противоположным знаком.

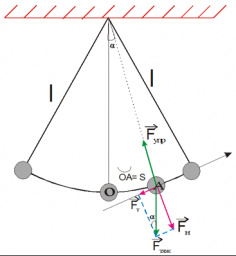
Знак минус появился потому, что сила и угол отклонения от положения равновесия α име­ют противоположные знаки. Для малых углов отклонения sin α ≈ α. В свою очередь, α = s/l, где s — дуга OA, I — длина нити. Учитывая, что а_τ = s», окончательно получим:

.

Вид уравнения аналогичен уравнению . Только здесь параметрами системы являются длина нити и ускорение свободного падения, а не жесткость пружины и масса шарика; роль координаты играет длина дуги (т. е. пройденный путь, как и в первом случае).

Таким образом, свободные колебания описываются уравнениями одного вида (подчиняются одним и тем же законам) независимо от физической природы сил, вызывающих эти колебания.

Решением уравнений и является функция вида:

То есть координата тела, совершающего свободные колебания, меняется с течением времени по закону косинуса или синуса, и, следовательно, эти колебания являются гармоническими:

В уравнении x = x_m cos ω₀ t (или x = x_m sin ω₀ t), х_m — амплитуда колебания, ω₀ — собственная циклическая (круговая) частота колебаний.

Циклическая частота и период свободных гармонических колебаний определяются свойствами системы. Так, для колебаний тела, прикрепленного к пружине, справедливы соотношения:

.

Собственная частота тем больше, чем больше жесткость пружины или меньше масса груза, что вполне подтверждается опытом.

Для математического маятника выполняются равенства:

.

Эта формула была впервые получена и проверена на опыте голландским ученым Гюйгенсом (современником Ньютона).

Период колебаний возрастает с увеличением длины маятника и не зависит от его массы.

Следует особо обратить внимание на то, что гармонические колебания являются строго периодическими (т. к. подчиняются закону синуса или косинуса) и даже для математического маятни­ка, являющегося идеализацией реального (физического) маятника, возможны только при малых углах колебания. Если углы отклонения велики, смещение груза не будет пропорционально углу отклонения (синусу угла) и ускорение не будет пропорционально смещению.

Скорость и ускорение тела, совершающего свободные колебания, также будут совершать гармонические колебания. Беря производную по времени функции (x = x_m cos ω₀ t (или x = x_m sin ω₀ t)), получим выражение для скорости:

где a_m = ω 2 ₀ x_m — амплитуда ускорения. Таким образом, амплитуда скорости гармонических коле­баний пропорциональна частоте, а амплитуда ускорения — квадрату частоты колебания.

Источник

Свободные колебания

Колебания – в той или иной степени повторяющийся во времени процесс изменения состояний системы около точки равновесия. Например, при колебаниях маятника повторяются отклонения его в ту и другую сторону от вертикального положения; при колебаниях в электрическом колебательном контуре повторяются величина и направление тока, текущего через катушку.

Колебания почти всегда связаны с попеременным превращением энергии одной формы проявления в другую форму. Колебания различной физической природы имеют много общих закономерностей и тесно взаимосвязаны с волнами. Поэтому исследованиями этих закономерностей занимается обобщенная теория колебаний и волн. Принципиальное отличие от волн: при колебаниях не происходит переноса энергии, это, так сказать, «местные» преобразования энергии.

Свободные колебания – колебания в системе под действием внутренних тел, после того как система выведена из положения равновесия. Колебания груза, подвешенного на нити, или груза, прикрепленного к пружине, – это примеры свободных колебаний. После выведения этих систем из положения равновесия создаются условия, при которых тела колеблются без воздействия внешних сил. Система – группа тел, движение которых мы изучаем. Внутренние силы – силы, действующие между телами системы. Внешние силы – силы, действующие на тела системы со стороны тел, не входящих в нее.

Условия возникновения свободных колебаний.

Для того чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению:

В этом соотношении \(\omega\) – круговая частота гармонических колебаний. Таким свойством обладает упругая сила в пределах применимости закона Гука:

Силы любой другой физической природы, удовлетворяющие этому условию, называются квазиупругими.

Таким образом, груз некоторой массы m, прикрепленный к пружине с жесткостью k, второй конец которой закреплен неподвижно, составляют систему, способную в отсутствие трения совершать свободные гармонические колебания. Груз на пружине называют линейным гармоническим осциллятором.

Круговая частота ω₀ свободных колебаний груза на пружине находится из второго закона Ньютона:

Частота ω₀ называется собственной частотой колебательной системы.

Период T гармонических колебаний груза на пружине равен

и колебания совершаются около этого нового положения равновесия. Приведенные выше выражения для собственной частоты \(ω_0\) и периода колебаний T справедливы и в этом случае.

Строгое описание поведения колебательной системы может быть дано, если принять во внимание математическую связь между ускорением тела a и координатой x: ускорение является второй производной координаты тела x по времени t:

Поэтому второй закон Ньютона для груза на пружине может быть записан в виде

Все физические системы (не только механические), описываемые уравнением (·), способны совершать свободные гармонические колебания, так как решением этого уравнения являются гармонические функции вида

Уравнение (·) называется уравнением свободных колебаний. Следует обратить внимание на то, что физические свойства колебательной системы определяют только собственную частоту колебаний \(ω_0\) или период T. Такие параметры колебательного процесса, как амплитуда \(x_m\) и начальная фаза φ₀, определяются способом, с помощью которого система была выведена из состояния равновесия в начальный момент времени.

Если же грузу, находившемуся в положении равновесия, с помощью резкого толчка была сообщена начальная скорость \(\pm v_0,\) то \(x_m=\sqrt<\frac mk>v_0,\varphi_0=\pm\frac \pi2.\)

Таким образом, амплитуда \(x_m\) свободных колебаний и его начальная фаза \(φ_0\) определяются начальными условиями.

Пе­ри­од ко­ле­ба­ний по­тен­ци­аль­ной энер­гии пру­жин­но­го ма­ят­ни­ка равен \(1\) с. Каким будет пе­ри­од ее ко­ле­ба­ний, если массу груза ма­ят­ни­ка и жест­кость пру­жи­ны уве­ли­чить в \(4\) раза?

Пе­ри­од ко­ле­ба­ний по­тен­ци­аль­ной энер­гии го­ри­зон­таль­но­го пру­жин­но­го ма­ят­ни­ка – \(1\) с. Каким будет пе­ри­од ее ко­ле­ба­ний, если массу груза ма­ят­ни­ка уве­ли­чить в \(2\) раза, а жест­кость пру­жи­ны вдвое умень­шить?

Гиря массой \(2\) кг подвешена на пружине жесткостью \(50\) Н/м. Период свободных колебаний груза

После отклонения от положения равновесия на \(1\) см математический маятник совершает свободные колебания с периодом в \(1\) с. При отклонении от положения равновесия на \(2\) см тот же маятник будет совершать колебания с периодом

Тело совершает \(120\) колебаний за \(2\) мин. Чему равны период и частота этих колебаний?

Как изменится период свободных колебаний маятника длиной \(10\) м, если амплитуды его колебаний увеличить от \(10\) см до \(20\) см?

Материальная точка совершает гармонические колебания по закону \(x = 0,07 \cdot \cos\big( πt + \frac<π> <2>\big)\) в единицах СИ. Определите амплитуду колебаний.

Найдите массу груза, который на пружине с жесткостью \(250\) Н/м за \(3,14\) с совершает \(5\) колебаний.

Периоды колебаний двух математических маятников относятся как 3:2. Первый маятник длиннее второго в

Шарик, подвешенный на пружине, за \( \frac<1><6>\) периода сместился от крайнего положения на \(15\) см. Определите амплитуду колебаний.

У математического маятника длиной \(250\) см период колебаний равен ( \(g\approx10\) м/с \(^2\) )

Шарик колеблется на пружине жесткостью \(0,25\) кН/м, при этом за \(16\) с совершает \(20\) колебаний. Определите его массу.

На графике показана зависимость смещения груза, совершающего колебания на пружинном маятнике, от времени. Жесткость пружины – \(0,1\) кН/м. Чему равна масса этого груза?

Чему равна циклическая частота колебаний груза массой \(18·10^3\) г, закрепленного на пружине жесткостью \(200\) Н/м?

Астронавт взял с собой на Луну математический маятник, который на Земле имел период колебаний \(2\) с. Изменится ли этот период колебаний на Луне?

В пруду на поверхности воды качается бумажный кораблик, длина волны – \(2,\!5\) м и она распространяется со скоростью \(120\) см/с. Определите период и частоту колебаний бумажного кораблика.

Амплитуда колебаний математического маятника равна \(8\) см, наибольшая скорость тела – \(0,2\) м/с. Чему равна длина этого маятника?

Чему равна частота колебаний груза массой \(40\) г на пружине жесткостью \(100\) Н/м?

Как изменится частота колебаний математического маятника, если его длину уменьшить в \(4\) раза?

Чему равна скорость волн, распространяющихся в озере, если поплавок совершает \(6\) колебаний за \(15\) секунд и расстояние между соседними горбами волны равно \(60\) см?

С какой частотой будет совершать колебания груз массой \(100\) г на пружине жесткостью \(40\) Н/м?

Чему равна длина математического маятника, если он совершает \(20\) колебаний за \(5\) с? ( \(g\approx10\) м/с \(^2\) )

Тело массой \(300\) г подвесили сначала на нити длиной \(1,5\) м, затем на пружине для совершения колебаний. При этом период колебаний в том и другом случае оказался одинаковым. Чему была равна жесткость пружины? ( \(g\approx10\) м/с \(^2\) )

Источник

Гармонические колебания

9 класс, 11 класс, ЕГЭ/ОГЭ

Механические колебания

Механические колебания — это физические процессы, которые точно или приблизительно повторяются через одинаковые интервалы времени.

Колебания делятся на два вида: свободные и вынужденные.

Свободные колебания

Это колебания, которые происходят под действием внутренних сил в колебательной системе.

Они всегда затухающие, потому что весь запас энергии, сообщенный в начале, в конце уходит на совершение работы по преодолению сил трения и сопротивления среды (в этом случае механическая энергия переходит во внутреннюю). Из-за этого свободные колебания почти не имеют практического применения.

Вынужденные колебания

А вот вынужденные колебания восполняют запас энергии внешним воздействием. Если это происходит каждый период, то колебания вообще затухать не будут.

Частота, с которой эта сила воздействует, равна частоте, с которой система будет колебаться.

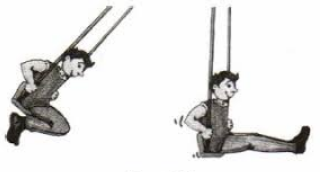
Например, качели. Если вас кто-то будет на них качать, каждый раз давая толчок, когда вы приходите в одну и ту же точку — такое колебание будет считаться вынужденным.

Это колебание все еще будет считаться вынужденным, если вас будут раскачивать из положения равновесия. Просто в данном случае амплитуда (о которой речь пойдет чуть ниже) будет увеличиваться с каждым колебанием.

Автоколебания

Иногда вынужденному колебанию не нужно внешнего воздействия, чтобы случиться. Бывают такие системы, в которых это внешние воздействие возникает само из-за способности регулировать поступление энергии от постоянного источника.

У автоколебательной системы есть три важных составляющих:

Часы с кукушкой — пример автоколебательной системы. Гиря на ниточке (цепочке) стремится вращать зубчатое колесо (храповик). При колебаниях маятника анкер цепляет за зубец, и вращение приостанавливается.

Но в результате маятник получает толчок, компенсирующий потери энергии из-за трения. Потенциальная энергия гири, которая постепенно опускается, расходуется на поддержание незатухающих колебаний.

Характеристики колебаний

Чтобы перейти к гармоническим колебаниям, нам нужно описать величины, которые помогут нам эти колебания охарактеризовать. Любое колебательное движение характеризуется величинами: период, частота, амплитуда, фаза колебаний.

Формула периода колебаний

T = t/N

N — количество колебаний [-]

Также есть величина, обратная периоду — частота. Она показывает, сколько колебаний совершает система в единицу времени.

Формула частоты

ν = N/t = 1/T

N — количество колебаний [-]

Она используется в уравнении гармонических колебаний:

Гармонические колебания

Простейший вид колебательного процесса — простые гармонические колебания, которые описывают уравнением:

Уравнение гармонических колебаний

x — координата в момент времени t [м]

t — момент времени [с]

2πνtв этом уравнении — это фаза. Ее обозначают греческой буквой φ

Фаза колебаний

t — момент времени [с]

Например, в тех же самых часах с кукушкой маятник совершает колебания. Он качается слева направо и приходит в самую правую точку. В той же фазе он будет находиться, когда придет в ту же точку, идя справа налево. Если мы возьмем точку на сантиметр левее самой правой, то идя в нее не слева направо, а справа налево, мы получим уже другую фазу.

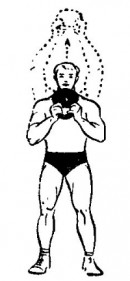
На рисунке ниже показаны положения тела через одинаковые промежутки времени при гармонических колебаниях. Такую картину можно получить при освещении колеблющегося тела короткими периодическими вспышками света (стробоскопическое освещение). Стрелки изображают векторы скорости тела в различные моменты времени.

Если изменить период, начальную фазу или амплитуду колебания, графики тоже изменятся.

На рисунке ниже во всех трех случаях для синих кривых начальная фаза равна нулю, а в последнем (с) — красная кривая имеет меньшую начальную фазу.

Во втором случае (b) красная кривая отличается от синей только значением периода — у красной период в два раза меньше.

Математический маятник

Математический маятник — отличный пример гармонических колебаний. Если мы подвесим шарик на нити, то это еще не будет математическим маятником — пока он только физический.

Математическим этот маятник станет, если размеры шарика много меньше длины нити (тогда этими размерами можно пренебречь и рассматривать шарик как материальную точку), растяжение нити очень мало, а масса нити во много раз меньше массы шарика.

Математическим маятником называется система, которая состоит из материальной точки массой m и невесомой нерастяжимой нити длиной l, на которой материальная точка подвешена, и которая находится в поле силы тяжести (или других сил).

Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле:

Формула периода колебания математического маятника

g — ускорение свободного падения [м/с^2]

На планете Земля g = 9,8 м/с2

Пружинный маятник

Пружинный маятник — это груз, прикрепленный к пружине, массой которой можно пренебречь.

В пружинном маятнике колебания совершаются под действием силы упругости.
Пока пружина не деформирована, сила упругости на тело не действует.

Формула периода колебания пружинного маятника

m — масса маятника [кг]

k — жесткость пружины [Н/м]

Закон сохранения энергии для гармонических колебаний

Физика — такая клевая наука, в которой ничего не исчезает бесследно и не появляется из ниоткуда. Эту особенность описывает закон сохранения энергии.

Рассмотрим его на примере математического маятника.

Источник

Механические колебания

теория по физике 🧲 колебания и волны

Колебательное движение очень распространено. Заставить колебаться можно любое тело, если приложить к нему силу — однократно или постоянно. К примеру, если подтолкнуть качели, они начнут качаться вперед-назад, и такое движение будет приблизительно повторяться до тех пор, пока качели полностью не остановятся.

Другой пример колебательного движения — тело, подвешенное к пружине. Если его потянуть вниз и отпустить, то за счет сил упругости оно сначала поднимется вверх, а затем снова опустится вниз, затем движения вверх-вниз будут повторяться. Со временем они прекратятся под действием силы сопротивления воздуха.

Колебаниями можно назвать даже движение гири, которую поднимается тяжелоатлет вверх, а затем опускает в низ. При этом он будет прикладывать к гире силу постоянно. Гиря будет колебаться до тех пор, пока к нему будет прикладываться эта сила.

Колебания — это движения, которые точно или приблизительно повторяются через определенные интервалы времени.

Механические колебания — это колебательные движения, совершаемые физическим телом в механической системе.

Механическая система — совокупность материальных точек (тел), движения которых взаимосвязаны между собой.

Какими бывают колебания?

Напомним, что в механической системе выделяют два вида сил:

Свободные колебания

Свободные колебания — колебания, происходящие в системе под действием внутренних сил после того, как эта система выведена из положения равновесия.

Колебательная система — механическая система, в которой возможно совершение свободных колебаний.

Свободные колебания в колебательной системе могут возникнуть только при наличии двух условий:

Примеры свободных колебаний:

Примером колебательной системы также служит математический маятник — материальная точка, подвешенная на невесомой нерастяжимой нити. В действительности такого маятника не существует. Это идеализированная модель реального маятника, примером которого служит тяжелый шарик, подвешенный на длинной нити. В этом случае размером шарика и растяжением нити можно пренебречь.

В колебательную систему математического маятника входят:

В положении равновесия (точка О) шарик висит на нити и покоится. Если его отклонить от положения равновесия до точки А и отпустить, под действием силы тяжести шарик приблизится к положению равновесия. Так как к этому моменту шарик обретет скорость, он не сможет остановиться и приблизится к точке В. Затем он снова вернется в точку А через положение равновесия в точке О. Шарик будет колебаться, пока не затухнут под действием возникающей силы сопротивления воздуха.

Вынужденные колебания

Вынужденные колебания — колебания тел под действием внешних периодически изменяющихся сил.

Примерами вынужденных колебаний служат:

Затухающие и незатухающие колебания

Затухающие колебания — колебания, которые со временем затухают. При этом максимальное отклонение тела от положения равновесия с течением времени уменьшается.

Колебания затухают под действием сил, препятствующих колебательному движению. Так, шарик в сферической чаше перестает колебаться под действием силы трения. Математический маятник и качели перестают совершать колебательные движения за счет силы сопротивления воздуха.

Все свободные колебания являются затухающими, так как всегда присутствует трение или сопротивление среды.

Незатухающими колебаниями могут быть только те, которые совершаются под действием периодической внешней силы (вынужденные колебания). Так, ветка будет раскачиваться до тех пор, пока дует ветер. Когда он перестанет дуть, колебания ветки со временем затухнут. Иголка швейной машинки будет совершать колебательные движения до тех пор, пока швея вращает ручку привода. Когда она перестанет это делать, иголка сразу остановится.

Динамика колебательного движения

Для того чтобы описать количественно колебания тела пол действием силы упругости пружины или колебания шарика, подвешенного на нити, воспользуемся законами механики Ньютона.

Уравнение движения тела, колеблющегося под действием сил упругости

Рассмотрим колебательное движение шарика, вызванное силой упругости, возникшей при растяжении горизонтальной пружины вдоль оси Ох.

Согласно II закону Ньютона произведение массы тела на ускорение равно равнодействующей всех сил приложенных к телу. Поскольку сила трения пренебрежимо мала, мы можем считать, что в этой механической системе действует единственная сила — сила упругости. Учтем, что шарик колеблется вдоль одной прямой, и выберем одномерную систему координат Ох. Тогда:

Согласно закону Гука, проекция сила упругости прямо пропорциональная смещению шарика из положения равновесия (точки О). Смещение равно координате x шарика, причем проекция силы и координаты имеют разные знаки. Это связано с тем, что сила упругости всегда направлена к точке равновесия, в то время как расстояние от этой точки во время движения увеличивается в обратную сторону. Отсюда делаем вывод, что сила упругости равна:

где k — жесткость пружины.

Тогда уравнение движения шарики принимает вид:

Пример №1. Груз массой 0,1 кг прикрепили к пружине школьного динамометра жесткостью 40 Н/м. В начальный момент времени пружина не деформирована. После того, как груз отпускают, возникают колебания. Чему равна максимальная скорость груза?

Максимальной скорости груз достигнет при максимальном его отклонении от положения равновесия — в нижней точке траектории. Учтем, что тело движется вниз под действием силы тяжести. Но в то же время на него действует сила упругости, которая возникает в пружине и нарастает до тех пор, пока не становится равной по модулю силе тяжести. Применив III закон Ньютона получим:

∣ ∣ ∣ → F т я ж ∣ ∣ ∣ = ∣ ∣ ∣ → F у п р ∣ ∣ ∣

где y m a x — максимальное отклонение груза от положения равновесия. В этой точке скорость тела будет максимальная. Для нахождения этой величины используем формулу из кинематики:

Начальная скорость равна нулю. Отсюда:

Максимальная скорость равна:

Уравнение движения математического маятника

Ниже на рисунке представлен математический маятник. Если мы выведем из положения равновесия шарик и отпустим, возникнет две силы:

При колебаниях шарика также будет возникать сила сопротивления воздуха. Но так как она очень мала, мы будем ею пренебрегать.

Чтобы описать динамику движения математического маятника, удобно силу тяжести разложить на две составляющие:

Причем компонента → F τ направлена перпендикулярно нити, а → F n — вдоль нее.

Компонента → F τ представляет собой проекцию силы тяжести в момент, когда нить маятника отклонена от положения равновесия (точки О) на угол α. Следовательно, она равна:

Знак «–» мы здесь поставили по той причине, что компоненты силы тяжести → F τ и α имеют противоположные знаки. Ведь если отклонить шарик на угол α>0, то составляющая → F τ будет направлена в противоположную сторону, так как она будет пытаться вернуть шарик в положение равновесия. И ее проекция будет отрицательной. Если же шарик отклонить на угол α → F τ будет направлена в обратную сторону. В этом случае ее проекция будет положительной.

Разделим обе части выражения на массу шарика m и получим:

Внимание! Чтобы перевести градусы в радианы, нужно умножить градусы на число π и поделить результат на 180. К примеру 2 о = 2∙3,14/180 рад., или 2 о = 0,035 рад.

При малом отклонении также дугу ОА мы можем принять за длину отрезка OA, который мы примем за s. Тогда угол α будет равен отношению противолежащего катета (отрезка s) к гипотенузе (длине нити l):

Это уравнение похоже на то уравнение, которое мы получили для описания колебательного движения шарика под действием силы упругости. И оно также позволяет сделать вывод, что ускорение прямо пропорционально координате.

При отклонениях на малый угол мы можем пользоваться следующей формулой:

Чтобы найти длину нити, нужно выразить угол α в радианах:

Тогда длина нити равна:

Основные характеристики колебательного движения

Амплитуда — максимальное отклонение тела от положения равновесия. Обозначается буквой A, иногда — x_max. Единиц измерения — метр (м).

Период — время совершения одного полного колебания. Обозначается буквой T. Единица измерения — секунда (с).

Период и частота колебаний связаны между собой следующей формулой:

Период колебаний также можно вычислить, зная количество совершенных колебаний N за время t:

Поскольку частота — это величина, обратная периоду колебаний, ее можно выразить в виде:

Пример №3. Определить частоту колебаний груза, если суммарный путь, который он прошел за 2 секунды под действием силы упругости, составил 1 м. Амплитуда колебаний равна 10 см.

Во время одного колебания груз проходит расстояние, равное 4 амплитудам. Посмотрите на рисунок. Положение равновесия соответствует состояние 2. Чтобы совершить одно полное колебание, сначала груз отводят в положение 1. Когда его отпускают, он проходит путь 1–2 и достигает положения равновесия. Этот путь равен амплитуде колебаний. Затем он продолжает движение до состояния 3. И в это время он проходит расстояние 2–3, равное еще одной амплитуде колебаний. Чтобы вернуться в исходное положение (состояние 1), нужно снова проделать путь в обратном направлении: сначала 3–2, затем 2–1.

Следовательно, количество колебаний равно отношению пройденного пути к амплитуде, помноженной на 4:

Так как мы знаем, что эти колебания совершались в течение 2 секунд, для вычисления частоты мы можем использовать формулу:

В таблице представлены данные о положении шарика, колеблющегося вдоль оси Ох, в различные моменты времени.

Каков период колебаний шарика?

Алгоритм решения

Решение

Из таблицы видно, что амплитуда колебаний равна 15 мм. Следовательно, максимальное отклонение в противоположную сторону составляет –15 мм. Расстояние между двумя максимальными отклонениями от положения равновесия шарика равно половине периода колебаний. Этим значения в таблице соответствует время 1 и 3 секунды соответственно. Следовательно, разница между ними — половина периода. Тогда период будет равен удвоенной разнице во времени:

T = 2 ( t 2 − t 1 ) = 2 ( 3 − 1 ) = 4 ( с )

pазбирался: Алиса Никитина | обсудить разбор | оценить

Массивный груз, подвешенный к потолку на пружине, совершает вертикальные свободные колебания. Пружина всё время остается растянутой. Как ведут себя потенциальная энергия пружины, кинетическая энергия груза, его потенциальная энергия в поле тяжести, когда груз движется вверх к положению равновесия?

Для каждой величины определите соответствующий характер изменения:

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения

Решение

Потенциальная энергия пружины определяется формулой:

где k — коэффициент жесткости пружины, а x — ее удлинение. Величина x была максимальной в нижней точке траектории. Когда пружина начинает сжиматься, она уменьшается. Так как потенциальная энергия зависит от квадрата x прямо пропорционально, то при уменьшении этой величины потенциальная энергия пружины тоже уменьшается.

Кинетическая энергия тела определяется формулой:

В нижней точке траектории скорость шарика была равна нулю. Но к этому времени потенциальная энергия пружины достигла максимума. Она начинает с ускорением поднимать шарик вверх, сжимаясь. Следовательно, скорость растет. Так как кинетическая энергия зависит от квадрата скорости тела прямо пропорционально, то при увеличении скорости этой величины кинетическая энергия шарика тоже увеличивается.

Потенциальная энергия тел в поле тяжести земли определяется формулой:

Масса и ускорение свободного падения шарика — постоянные величины. Следовательно, потенциальная энергия зависит только от расстояния до поверхности земли. Когда пружина поднимает шарик, расстояние между ним и землей увеличивается. Так как потенциальная энергия зависит от расстояния прямо пропорционально, то при его увеличении потенциальная энергия шарика тоже растет.

pазбирался: Алиса Никитина | обсудить разбор | оценить

В таблице представлены данные о положении шарика, прикреплённого к пружине и колеблющегося вдоль горизонтальной оси Ох, в различные моменты времени.

Из приведённого ниже списка выберите два правильных утверждения и укажите их номера.

А) Потенциальная энергия пружины в момент времени 1,0 с максимальна.

Б) Период колебаний шарика равен 4,0 с.

В) Кинетическая энергия шарика в момент времени 2,0 с минимальна.

Г) Амплитуда колебаний шарика равна 30 мм.

Д) Полная механическая энергия маятника, состоящего из шарика и пружины, в момент времени 3,0 с минимальна.

Алгоритм решения

Решение

Согласно утверждению «А», потенциальная энергия пружины в момент времени 1,0 с максимальна. Потенциальная энергия пружины максимальна, когда она отклоняется от положения равновесия на максимальную возможную величину. Из таблицы видно, что в данный момент времени ее отклонение составило 15 мм, что соответствует амплитуде колебаний (наибольшему отклонению от положения равновесия). Следовательно, утверждение «А» — верно.

Согласно утверждению «Б», период колебаний шарика равен 4,0 с. Один период колебаний включает в себя 4 фазы. В течение каждой фазы шарик на пружине проделывает путь, равный амплитуде. Следовательно, мы можем найти период колебаний, умножив время одной фазы на 4. В момент времени t = 0 с, шарик находился в положении равновесия. Первый раз он отклонился на максимальную величину (15 мм) в момент времени t = 1,0 с. Значит, период колебаний равен 1∙4 = 4 с. Следовательно, утверждение «Б» — верно.

Согласно утверждению «В», кинетическая энергия шарика в момент времени 2,0 с минимальна. В этот момент времени, согласно данным таблицы, шарик проходит положение равновесия. В этом положении скорость шарика всегда максимальна. Поэтому кинетическая энергия, которая зависит от квадрата скорости прямо пропорционально, минимальной быть не может. Следовательно, утверждение «В» — неверно.

Согласно утверждению «Г», амплитуда колебаний шарика равна 30 мм. Амплитуда колебаний — есть расстояние от положения равновесия до точки максимального отклонения шарика. В данном случае оно равно 15 мм. Следовательно, утверждение «Г» — неверно.

Согласно утверждению «Д», полная механическая энергия маятника, состоящего из шарика и пружины, в момент времени 3,0 с минимальна. Полная механическая энергия колебательной системы — это совокупность кинетической и потенциальной энергий. И при отсутствии сил трения она остается величиной постоянной. Она лишь превращается из одного вида энергии в другую. Следовательно, утверждение «Д» — неверно.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник