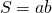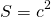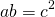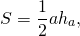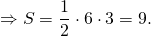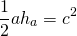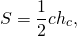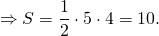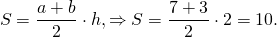что такое равные фигуры
Равновеликие фигуры
Равновеликие фигуры — это фигуры, которые имеют одинаковые площади.
Равновеликие тела — это тела, которые имеют равные объёмы (равновеликие тела часто также называют равновеликими фигурами). Равные фигуры — это фигуры, которые совпадают при наложении (у них соответствующие стороны равны и соответствующие углы равны).
Равные фигуры имеют равные площади, поэтому равные фигуры являются также равновеликими. Обратное, вообще говоря, неверно.
1) Прямоугольник и квадрат, изображенные на рисунке 1, — равновеликие фигуры.
То есть, прямоугольник со сторонами a и b и квадрат со стороной c являются равновеликими, если
2) Треугольник и квадрат, изображенные на рисунке 2 — равновеликие фигуры, так как имеют равные площади.
Площадь квадрата S=3²=9.
Треугольник со стороной a и проведенной к ней высоте ha и квадрат со стороной c являются равновеликими, если
3) Треугольник и трапеция, изображенные на рисунке 3 — равновеликие, поскольку их площади равны.
Треугольник со стороной c и проведенной к ней высотой hс и трапеция с основаниями a и b и высотой h являются равновеликими, если
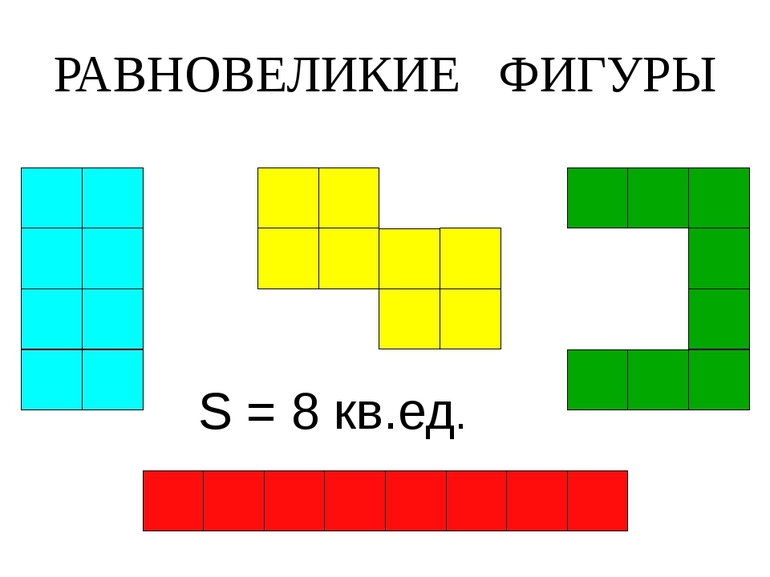
Равные многоугольники
По определению равные фигуры должны быть во всём одинаковыми, включая площадь, длину сторон, размер углов и другие параметры. Чтобы рассмотреть всё из них, уйдёт много времени, да это и не нужно, ведь они взаимозависимы. Хорошим примером будет самый простой многоугольник — треугольник. Существует несколько правил, по которым можно определить, равны ли 2 треугольника между собой или нет:
Нельзя путать первое условие с тремя углами. Ведь если в треугольнике равны 3 угла, они необязательно будут равными, но будут подобными.
Названия условий достаточно точно описывают критерии, по которым можно определить одинаковые 2 треугольника или нет. Из них следует, что необязательно знать все параметры: часто хватает только нескольких из них для определения «равности».
В большинстве случаев определить одинаковость других фигур гораздо сложнее, нежели треугольников. К счастью, чаще всего в школьной геометрии такой класс задач не рассматривают или даются дополнительные данные, помогающие с решением.
Например, доказательство «равности» для четырёхугольника сложнее, да и почти не встречается. Но если по условию сказано, что четырёхугольник не произвольный, а имеет прямые углы, задача становится проще. В таком случае рассматривается прямоугольник. А для него достаточно, чтобы 2 не противолежащие стороны были равны.
Если указано ещё и условие, что прямоугольник является квадратом, достаточно указать, что у двух таких фигур совпадает по длине одна сторона и уже этого будет достаточно.
Равность правильных фигур
Частным и самым простым для сравнения является случай, когда многоугольник по условию правильный. Так называется фигура с одинаковыми сторонами и углами. Например, равносторонний треугольник и квадрат. Важно не забывать проверить равны ли углы, так как не каждая фигура правильная. Тот же ромб по определению имеет 4 совпадающие по длине стороны, но разные углы. При сравнении правильных многоугольников достаточно указать, что, хотя бы одна сторона фигуры равна стороне у другой. Это будет достаточное условие для доказательства «равности».
Самым простым и наглядным способом сверки двух фигур будет не геометрический с помощью правил, а путём наложения рисунков друг на друга. Разумеется, что он не претендует на точность, но изобразить параллелограмм и наложить его на другой нагляднее, чем сравнивать, например, углы. Понятно, что так можно только ознакомиться с концепцией «равности» и показать, какие фигуры называются равными, для упрощения в дальнейшем решения задач, но доказывать что-либо нельзя, ввиду неточности метода.
Если при сравнении двух тел оказывается, что их площади равны, такие тела (многоугольники) являются равновеликими. Как и в случае с прошлым, это определение звучит несложно. Проблемы могут начаться непосредственно при вычислении площадей. Самый простой многоугольник — треугольник. Для вычисления его площади существует множество способов.
Вычисление площади треугольника
Чаще всего приходится работать с прямоугольными треугольниками. Их площадь вычислить несложно — это полупроизведение катетов (сторон, между которыми лежит прямой угол). Таким образом, даже если стороны двух фигур по длине разные, но их произведение равно, они равновеликие. Например, треугольник с катетами 4 и 4 равен по площади многоугольнику с катетами 16 и 1. Так как их полупроизведение, а значит и площадь равна 8.
Если же треугольник произвольный (то есть не является частным случаем — прямоугольным, равнобедренным или равносторонним), можно воспользоваться одной из 5 формул, позволяющих вычислить его площадь.
То, какую формулу использовать, будет зависеть от данных, предоставленных в задаче. Иногда придётся проводить дополнительное построение, например, провести высоту или использовать свойства, что биссектрисы пересекаются в центре вписанной окружности. Если не даны все 3 стороны, использовать третью формулу не получится.
Важно понять, что фигуры могут быть разными по количеству углов, но всё равно считаться равновеликими — в учёт идёт только площадь, остальные параметры не важны. Например, прямоугольный треугольник с катетами 2 и 4 будет визуально казаться больше, чем квадрат со стороной 2, но их площади совпадают и равны 4 (площадь прямоугольника считается как произведение прилежащих сторон друг на друга). По определению это делает их равновеликими.
Визуальный способ
Существует также наглядный, но неточный способ. Нужно взять листок в клеточку и нарисовать на нём многоугольники. Если рисунок получился большой — не страшно, так будет только проще в дальнейшем. Следующий шаг — посчитать количество клеток, которое заняла каждая фигура и сравнить. Если оно равно, равновеликость доказана. Опять же метод не точный, но для введения в концепцию площадей и их «равности» подойдёт.
Иногда встречается словосочетание «равносоставленная фигура». Такими называют произвольные многоугольники, которые можно составить друг из друга путём разрезания одного из них на одинаковые объекты и перекладывания. Например, если прямоугольник 4 на 1 нарезать на одинаковые части — квадраты 1 на 1, то из полученных маленьких квадратов можно составить один большой со стороной 2. Но это не более чем забавное свойство некоторых фигур и в геометрии фактически почти не используется.
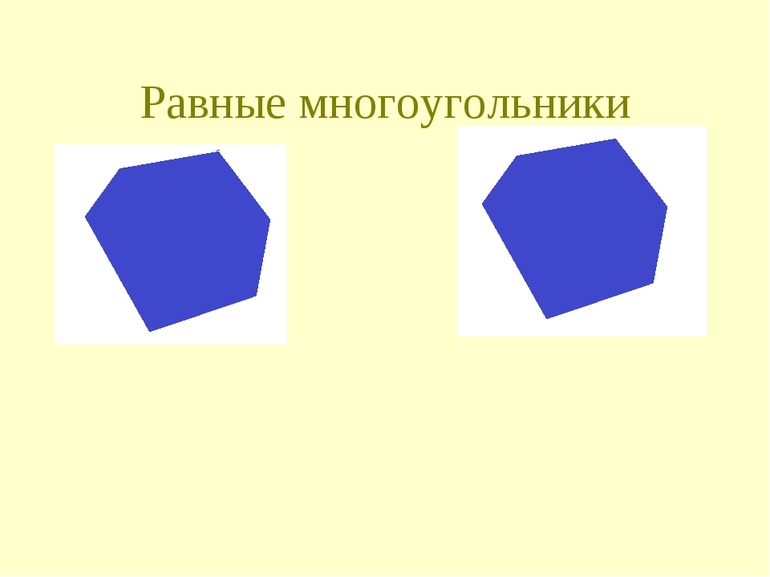
Какие фигуры называются равными
Содержание статьи
Геометрические фигуры могут рассматриваться не изолированно, а в том или ином соотношении друг с другом – их взаимное расположение, соприкосновение и прилегание, положение «между», «внутри», соотношение, выраженное в понятиях «больше», «меньше», «равно».
Геометрия изучает инвариантные свойства фигур, т.е. те, которые остаются неизменными при тех или иных геометрических преобразованиях. Такое преобразование пространства, при котором остается неизменным расстояние между точками, составляющими ту или иную фигуру, называется движением.
Движение может выступать в разных вариантах: параллельный перенос, тождественное преобразование, поворот вокруг оси, симметрия относительно прямой или плоскости, центральная, поворотная, переносная симметрия.
Движение и равные фигуры
Если возможно такое движение, которое приведет к совмещению одной фигуры с другой, такие фигуры называют равными (конгруэнтными). Две фигуры, равные третьей, равны и между собою – такое утверждение было сформулировано еще Евклидом, основоположником геометрии.
Понятие конгруэнтных фигур может быть объяснено и более простым языком: равными называются такие фигуры, которые полностью совпадут при наложении их друг на друга.
Это достаточно легко определить, если фигуры даны в виде неких предметов, которыми можно манипулировать – например, вырезаны из бумаги, поэтому в школе на уроках нередко прибегают к такому способу объяснения данного понятия. Но две фигуры, начерченные на плоскости, нельзя физически наложить друг на друга. В данном случае доказательством равенства фигур выступает доказательство равенства всех элементов, составляющих эти фигуры: длина отрезков, размер углов, диаметр и радиус, если речь идет об окружности.
Равновеликие и равносоставленные фигуры
С равными фигурами не следует смешивать равновеликие и равносоставленные фигуры – при всей близости данных понятий.
Равновеликими называются такие фигуры, которые имеют равную площадь, если это фигуры на плоскости, или равный объем, если речь идет о трехмерны телах. Совпадение всех элементов, составляющих данные фигуры, не является обязательным. Равные фигуры будут равновеликими всегда, но не всякие равновеликие фигуры можно назвать равными.
Понятие равносоставленности чаще всего применяют к многоугольникам. Оно подразумевает, что многоугольники можно разбить на одинаковое количество соответственно равных фигур. Равносоставленные многоугольники всегда являются равновеликими.
Многоугольники. Равные фигуры
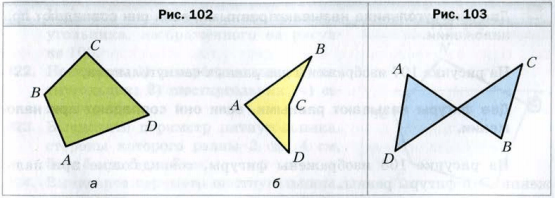
На рисунках 102 и 103 изображены три фигуры, каждая из которых ограничена замкнутой ломаной, состоящей из четырех звеньев AB, BC, CD, DA.
Фигуры, изображенные на рисунке 102, называют четырехугольниками.
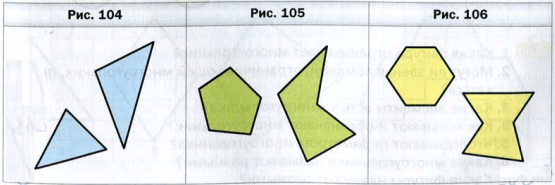
На рисунке 104 изображены треугольники, на рисунке 105 − пятиугольники, на рисунке 106 − шестиугольники.
Все эти фигуры являются примерами многоугольников. Фигура, изображенная на рисунке 103, многоугольником не является.
Каждый многоугольник имеет вершины и стороны. Так, на рисунке 102, a точки A, B, C, D − вершины четырехугольника, отрезки AB, BC, CD, DA − его стороны, а углы A, B, C, D − углы четырехугольника.
Многоугольник называют и обозначают по его вершинам. Для этого надо последовательно записать или назвать все его вершины, начиная с любой.
Изображенные на рисунке 102 четырехугольники можно назвать, например, так : ABCD, или BCDA, или DCBA и т.п.
Сумму длин всех сторон многоугольника называют его периметром.
Два многоугольника называют равными, если они совпадают при наложении.
На рисунке 107 изображены два равных семиугольника.
Две фигуры называют равными, если они совпадают при наложении.
На рисункее 108 изображены фигуры, совпадающие при наложении. Эти фигуры равны.
Презентация по математике на тему «Многоугольники. Равные фигуры»
Описание презентации по отдельным слайдам:
Описание слайда:
Многоугольники.
Равные фигуры
Описание слайда:
Что изображено на чертеже?
Описание слайда:
Что изображено на чертеже?
Описание слайда:
Описание слайда:
Описание слайда:
Многоугольник-это геометрическая фигура,
образованная замкнутой ломаной линией
ломанная линия
А
С
E
B
Описание слайда:
Из истории многоугольников
В древних египетских и вавилонских математических рукописях понятие четырехугольника встречается около 5 тыс. лет назад.
Квадрат и прямоугольник –
греческие прямоугольники,
трапеция – греческий столик.
Описание слайда:
Определите вид многоугольника
1
5
2
3
Описание слайда:
Описание слайда:
Данная фигура не является многоугольником …
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Два многоугольника (две фигуры) называют равными, если они совпадают при наложении.
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
Описание слайда:
С. 87, №321 (устно), №322, №323,
№325, 333
Работа по учебнику:
Описание слайда:
Описание слайда:
§13, в. 1-7
№ 324,
№ 326,
№ 335
Желаю удачи!
Домашнее задание
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
также Вы можете выбрать тип материала:
Общая информация
Международная дистанционная олимпиада Осень 2021
Похожие материалы
Презентация по математике на тему «Проценты. Нахождение процентов от числа»
Программа по математике для 4 класса
Презентация по математике на тему «Объем прямоугольного параллелепипеда»
Проект по математике «Математика вокруг нас. Числа в загадках, пословицах, поговорках».
Карточка по математике на тему «Таблица умножения и деления с числом 4.» » (3класс)
Технологическая карта математика docx
Презентация по математике на тему «Сокращение дробей» (6 класс)
Презентация по математике (4класс)
Не нашли то что искали?
Воспользуйтесь поиском по нашей базе из
5323975 материалов.
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Педагогов и учеников предлагают тренировать на случай нападения
Время чтения: 1 минута
Кузнецова призвала разработать закон о психологической помощи
Время чтения: 1 минута
На новом «Уроке цифры» школьникам расскажут о разработке игр
Время чтения: 1 минута
ФИПИ опубликовал демоверсии ОГЭ и ЕГЭ 2022
Время чтения: 1 минута
В МГУ разрабатывают школьные учебники с дополненной реальностью
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.