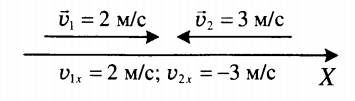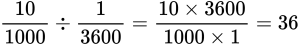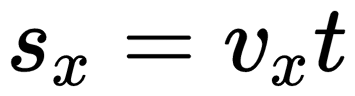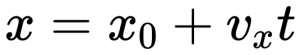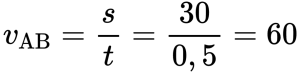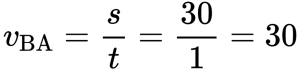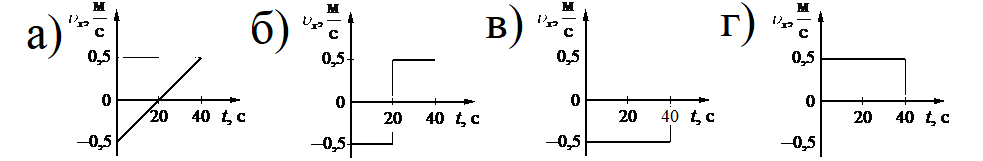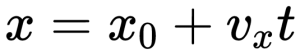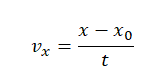что такое равномерное движение в физике определение

Равномерное движение

Равномерное движение

Для кинематического описания движения расположим ось OХ вдоль направления движения. Для определения перемещения тела при равномерном прямолинейном движении достаточно одной координаты Х. Проекции перемещения и скорости на координатную ось можно рассматривать, как алгебраические величины.

В зависимости от направления оси и направления движения тела эта величина может быть как положительной, так и отрицательной. При прямолинейном и равномерном движении модуль перемещения тела совпадает с пройденным путем. Скорость равномерного прямолинейного движения определяется по формуле:

Математическое описание равномерного прямолинейного движения

Закон движения тела при равномерном прямолинейном движении описывается линейным алгебраическим уравнением.

Уравнение движения тела при равномерном прямолинейном движении

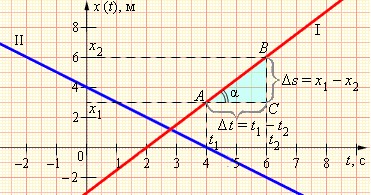
От точки x 1 до точки x 2 тело переместилось за две секунды. Перемещение тела составило три метра.

Зная это, можно найти скорость тела.

Есть еще один способ определения скорости: из графика ее можно найти как отношение сторон BC и AC треугольника ABC.

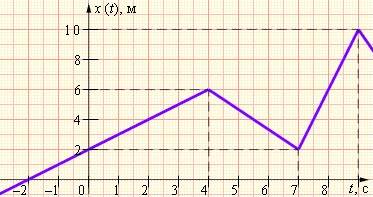
Аналогично вычисления проводятся для второго случая движения. Рассмотрим теперь новый график, изображающий движение с помощью отрезков прямых. Это так называемый кусочно-линейный график.

Отметим, что путь и перемещение не совпадают для движения, описываемого кусочно-линейным графиком. Например, в интервале времени от нуля до семи секунд тело прошло путь, равный 8 метрам. Перемещение тела при этом равно нулю.

Источник

Равномерное прямолинейное движение

теория по физике 🧲 кинематика

Равномерное прямолинейное движение — это такое движение, при котором тело совершает за любые равные промежутки времени равные перемещения.

Скорость при прямолинейном равномерном движении

Если тело движется равномерно и прямолинейно, его скорость остается постоянной как по модулю, так и по направлению. Ускорение при этом равно нулю.

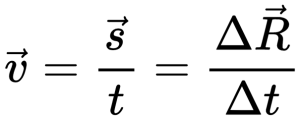
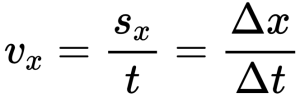
Векторный способ записи скорости при равномерном прямолинейном движении:s — вектор перемещения, ΔR— изменение радиус-вектора, t — время, а ∆t — его изменение. Проекция скорости на ось ОХ: s_x — проекция перемещения на ось ОХ, ∆x — изменение координаты точки (ее абсциссы). Знак модуля скорости зависит от направления вектора скорости и оси координат:

Основная единица измерения скорости — 1 метр в секунду. Сокращенно — 1 м/с.

Спидометр — прибор для измерения модули скорости тела.

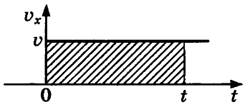
График зависимости скорости от времени представляет собой прямую линию, перпендикулярную оси скорости и параллельную оси времени. Выглядит он так:

Чтобы сравнить модули скоростей на графике, нужно оценить их удаленность от оси времени. Чем дальше график от оси, тем больше модуль.

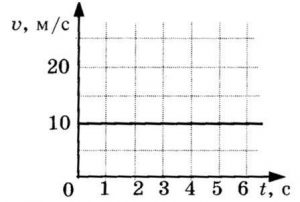
Пример №1. Найти модуль скорости и направление движения тела относительно оси ОХ. Выразить скорость в км/ч.

График скорости пересекает ось в точке со значением 10. Единица измерения — м/с. Поэтому модуль скорости равен 10 м/с. График лежит выше оси времени. Это значит, что тело движется по направлению оси ОХ. Чтобы выразить скорость в км/ч, нужно перевести 10 м в километры и 1 с в часы:

Теперь нужно разделить километры на часы:

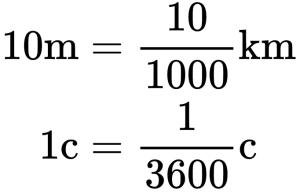
Перемещение и координаты тела при равномерном прямолинейном движении

Геометрический смысл перемещения заключается в том, что его модуль равен площади фигуры, ограниченной графиком скорости, осями скорости и времени, а также линией, проведенной перпендикулярно оси времени.

При прямолинейном равномерном движении эта фигура представляет собой прямоугольник. Поэтому модуль перемещения вычисляется по следующей формуле:

Вектор перемещения равен произведению вектора скорости на время движения: Внимание!

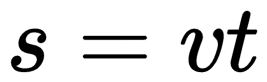
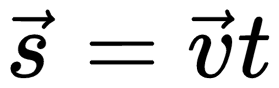
При равномерном прямолинейном движении путь и перемещение совпадают. Поэтому путь, пройденный телом, можно найти по этим же формулам.

Формула проекции перемещения:

График проекции перемещения

График проекции перемещения показывает зависимость этой проекции от времени. При прямолинейном равномерном движении он представляет собой луч, исходящий из начала координат. Выглядит он так:

Чтобы по графику проекции перемещения сравнить модули скоростей, нужно сравнить углы их наклона к оси s_x.Чем меньше угол, тем больше модуль. Согласно рисунку выше, модули скорости тел, которым соответствуют графики 1 и 3, равны. Они превосходят модуль скорости тела 2, так как их угол наклона к оси s_x меньше.

График координаты

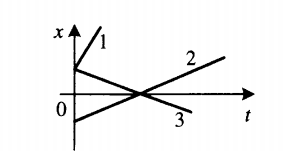
График координаты представляет собой график зависимости координаты от времени. Выглядит он так:

Так как график координаты представляет собой график линейной функции, уравнение координаты принимает вид :

Чтобы сравнить модули скоростей тел по графику координат, нужно сравнить углы наклона графика к оси координат. Чем меньше угол, тем больше модуль скорости. На картинке выше наибольший модуль скорости соответствует графику 1. У графиков 2 и 3 модули равны.

Чтобы по графику координат найти время встречи двух тел, нужно из точки пересечения их графиков провести перпендикуляр к оси времени.

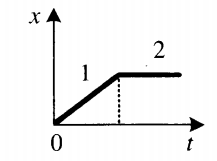
Пример №2. График зависимости координаты тела от времени имеет вид:

Изучите график и на его основании выберите два верных утверждения:

На участке 1 координата растет, и ее график представляет собой прямую. Это значит, что на этом участке тело движется равномерно (с постоянной скоростью). На участке 2 координата с течением времени не меняется, что говорит о том, что тело покоится. Исходя из этого, верными утверждениями являются номера 1 и 3.

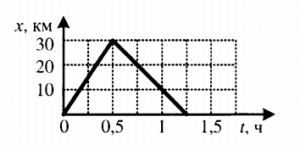
Пример №3. На рисунке изображен график движения автомобиля из пункта А (х=0 км) в пункт В (х=30 км). Чему равна минимальная скорость автомобиля на всем пути движения туда и обратно?

Согласно графику, с начала движения до прибытия автомобиля в пункт 2 прошло 0,5 часа. А с начала движения до возвращения в пункт А прошло 1,5 часа. Поэтому время, в течение которого тело возвращалось из пункта В в пункт А, равно:

Туда и обратно автомобиль проходил равные пути, каждый из которых равен 30 км. Поэтому скорость во время движения от А к В равна:

Скорость во время движения от В к А равна:

Минимальная скорость автомобиля на всем пути движения составляет 30 км/ч.

На рисунке представлены графики зависимости пройденного пути от времени для двух тел. Скорость второго тела v₂ больше скорости первого тела v₁ в n раз, где n равно…

Алгоритм решения

Решение

Рассмотрим графики во временном интервале от 0 до 4 с. Ему соответствуют следующие данные:

Скорость определяется формулой:

Так как начальный момент времени и скорость для обоих тел нулевые, формула примет вид:

Скорость первого тела:

Скорость второго тела:

Отношение скорости второго тела к скорости первого тела:

pазбирался: Алиса Никитина | обсудить разбор | оценить

На рисунке приведён график зависимости координаты тела от времени при прямолинейном движении тела по оси Ox.

Алгоритм решения

Уравнение координаты при равномерном прямолинейном движении имеет вид:

Отсюда проекция скорости равна:

Начальная координата x_o = 10 м, конечная x = –10 м. Общее время, в течение которого двигалось тело, равно 40 с.

Вычисляем проекцию скорости:

Этому значению соответствует график «в».

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

Решение

Весь график можно поделить на 3 участка:

По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t₁ = 20 c до t₂ = 50 с. Этому времени соответствуют два участка:

Записываем формулу искомой величины:

s₁ — путь тела, пройденный на первом участке, s₂ — путь тела, пройденный на втором участке.

s₁и s₂ можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:

Теперь рассчитаем пути s₁и s₂, а затем сложим их:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник

Равномерное механическое движение. Равномерное движение и его график

Равномерное движение считается самым простым из всех видов механического движения. Для него характерно отсутствие ускорения. Проще говоря, равномерным движением есть такое идеальное движение, когда скорость тела не меняется и остаётся одинаковой на протяжении длительного времени. Когда тело преодолевает равные расстояния за одинаковые интервалы времени, движение называют равномерным прямолинейным. Однако такое идеальное движение в жизни бывает крайне редко.

Стоит различать данные понятия, поскольку они имеют разный физический смысл. Путь есть величиной скалярной, а перемещение – векторной. Кроме того, по длине перемещение и путь могут отличаться, так как путь показывает длину всей траектории движения объекта, а перемещение – лишь расстояние между началом и концом его движения. Перемещение и путь могут иметь одинаковую длину лишь в случае прямолинейного движения.

Скорость равномерного движения

То есть, вектор скорости равномерного движения направлен в сторону движения тела. Про это следует помнить при изображении графика равномерного движения.

Особенностью прямолинейного равномерного движения является равенство пути и перемещения.

Частным случаем равномерного движения есть состояние покоя. При этом условие равномерного движения выполняется, поскольку все главные характеристики движения равняются нулю.

Не нашли что искали?

Просто напиши и мы поможем

Построение графиков равномерного движения

Если построить график зависимости скорости от времени равномерного движения, то он будет выглядеть как прямая, параллельная оси абсцисс, и удалённая от неё на величину скорости. При этом, если задать на данном графике интервал времени, то площадь получившегося прямоугольника будет показывать значение пройденного пути. Другими словами, произведение двух его сторон – скорости и времени.

Если построить график зависимости пройденного пути от времени при равномерном движении, то можно определить скорость, с которой данное движение было совершено. Данный график будет иметь вид прямой, выходящей из начала координат. В таком случае скорость равномерного движения будет определяться тангенсом угла наклона прямой к оси абсцисс. Чем меньше угол наклона графика, тем меньше скорость равномерного движения.

Физики часто используют такое выражение для равномерного движения:

Физический смысл данного выражения заключается в том, что скорость является константой, то есть не меняется во времени.

Равномерное движение может происходить как по прямой, так и криволинейно.

Для описания зависимости основных характеристик механического движения при равномерном передвижении используют следующую формулу:

где \(s\) – путь, преодоленный телом от начала отсчёта;

\(s_0\) – значение пути в начальный момент времени;

\(v\) – скорость передвижения.

Прямолинейное движение

Если движение тела является прямолинейным и равномерным, то направление и значение скорости не зависят от времени. То есть, вектор перемещения и вектор скорости направлены одинаково. При этом величина средней скорости совпадает со значением мгновенной скорости в любой момент времени в любой точке траектории.

Скорость равномерного прямолинейного движения будет показывать перемещение объекта за единицу времени.

Сложно разобраться самому?

Попробуй обратиться за помощью к преподавателям

Равнопеременное движение

Равнопеременное прямолинейное движение есть частным случаем неравномерного движения.

Для него характерна смена скорости тела на равные значения за одинаковые интервалы времени. Проще говоря, для равнопеременного движения характерно постоянное по модулю и направлению ускорение:

Различают равноускоренное и равнозамедленное равнопеременное движение.

При равноускоренном движении ускорение имеет знак «плюс», при этом тело постоянно равномерно разгоняется.

При равнозамедленном движении ускорение имеет знак «минус», при этом тело постоянно равномерно притормаживает.

При равнопеременном движении используют понятие средней скорости, значение которой рассчитывается отношением перемещения объекта к интервалу времени.

Понятие ускорения и мгновенной скорости

Мгновенной скоростью считается значение скорости движения тела, зафиксированное в заданный момент времени. Значение мгновенной скорости есть предельным, так как при бесконечном стремлении интервала времени \(∆t\) к нулю оно постоянно стремится к значению средней скорости.

При этом значение мгновенной скорости рассчитывают так:

Ускорение показывает изменение скорости тела. Эта величина также является предельной при бесконечном стремлении интервала времени \(∆t\) к нулю.

Перемещение тела при равномерном прямолинейном движении рассчитывают таким образом:

где \(v_x\) является проекцией скорости на ось абсцисс.

В результате этого закон прямолинейного равномерного движения запишется так:

Источник

Равномерное и неравномерное движение

Содержание

В прошлом уроке мы дали определение механическому движению; узнали, что оно относительно; рассмотрели такие характеристики как траектория и путь.

Движение бывает прямолинейным и криволинейным. Но, как вы уже догадываетесь, у движения есть и другие важные характеристики. В данном уроке вы познакомитесь с определениями равномерного и неравномерного движения.

Равномерное движение

Рассмотрим две ситуации. В первой мы наблюдаем за автомобилем. Он движется по пустой прямой дороге.
Во второй ситуации мы видим, как ребенок скатывается на санках с горки. Что объединяет эти две ситуации?

В обоих случаях тела движутся по прямой линии, т.е. совершают прямолинейное движение. Но, если машина за каждую минуту проезжает по одному километру, то про санки мы не можем сказать то же самое.

Итак, машина за каждые 5 минут проедет 5 км, за каждые полчаса (30 мин) – 30 км, за каждый час (60 мин) – 60 км. В таком случае говорят, что тело движется равномерно.

Равномерное движение – это механическое движение, при котором тело за любые равные промежутки времени проходит равные пути.

При равномерном движении скорость не изменяется

Мы должны понимать, что в реальной жизни водителю не удастся поддерживать долгое время равномерность движения: на дороге возникают другие машины, светофоры, пешеходы.

Но что же тогда будет являться примером равномерного движения? Взгляните на рисунок 1.

Рисунок 1. Время полного оборота вокруг Солнца планет Солнечной системы.

Планеты движутся вокруг Солнца равномерно. Земля каждый раз делает полный оборот за 365 дней (1 год), Юпитер за 11 лет, Нептун за 165 и т.д.

Неравномерное движение

Вернемся к рассматриваемой ситуации с санками. Очевидно, что с течением времени, они проходят все большие и большие участки пути, т.е. движутся неравномерно, так как их скорость постоянно увеличивается.

Неравномерное движение – это движение, при котором тело за равные промежутки времени проходит разные пути.

Рассмотрим простой опыт, который поможет нам лучше разобраться с этим определением. На рисунке 2 изображена тележка с капельницей. Из капельницы каждую 1 секунду падает капля.

Когда тележка начинает двигаться под действием груза, к которому она привязана, мы видим, что расстояние между каплями неодинаково. Это означает, что тележка двигается неравномерно, т.е. проходит разные пути за равные промежутки времени.

Рисунок 2. Неравномерное движение на примере движения тележки с капельницей.

Неравномерное движение встречается гораздо чаще, чем равномерное. Реальное движение автомобиля в городе – пример неравномерного движения.

Поезд, отходя от станции, движется неравномерно, потому что за одинаковые промежутки времени проходит все большие и большие пути.

Рассмотрим следующий интересный пример. Если вы взгляните на механические часы, то вам может показаться, что минутная и часовая стрелки движутся равномерно. Но это не так, и вы легко можете убедиться в этом, взглянув на секундную стрелку. Она движется скачкообразно, с остановками – это неравномерное движение. Значит, минутная и часовая стрелки движутся так же, но медленно, поэтому их рывков не видно.

Источник

Что такое равномерное движение в физике определение

2.1 Равномерное прямолинейное движение.

2.1.1 Равномерное прямолинейное движение — это движение, при котором тело за любые равные промежутки времени совершает равные перемещения, двигаясь по прямой линии.

2.1.2 Скорость — векторная физическая величина, показывающая какое перемещение совершило тело за единицу времени:

При равномерном движении по прямой:

где S — путь, проходимый телом за время t.

Для учета направления движения эту формулу запишем в проекциях:

где — перемещение вдоль оси Ox за время t. Знак проекции зависит от направления скорости и оси координат (см. рис.):

2.1.3 График проекции скорости от времени.

Так скорость при равномерном движении по прямой является постоянной, то график будет представлять собой прямые линии, параллельные оси времени (см. рис.):

Направление движения: если график лежит над осью времени (1 и 2), то проекция положительна и тело движется по направлению оси Ox; в противном случае, когда график расположен ниже оси времени (3 и 4), то проекция скорости отрицательна и тело движется против оси Ox.

Значение скорости: чем дальше от оси времени лежит прямая, тем больше модуль скорости

2.1.4 Геометрический смысл площади под графиком в осях .

Для любого вида движения пройденный телом путь можно определить как площадь под графиком, когда на оси Oy отложена скорость, а на оси Ox — время. Это легко видеть непосредственно из рисунка для равномерного движения (см. рис.):

2.1.5 График проекции перемещения.

Проекция перемещения при равномерном прямолинейном движении определяется формулой:

График проекции перемещения при равномерном прямолинейном движении — это прямая, выходящая из начала координат.

Направление движения: если прямая лежит над осью времени (поднимается вверх), то тело движется в положительном направлении оси Ox (прямые 1 и 2); если прямая лежит под осью времени (опускается вниз), то тело движется против оси Ox.

Значение скорости: чем больше тангенс угла наклона (чем круче поднимается вверх или опускает вниз), тем больше модуль скорости

2.1.6 Закон движения.

где — начальная координата тела по оси Ox, x — координата тела в момент времени t, — проекция скорости на ось Ox.

При движении по прямой всегда возможно выбрать ось Ox вдоль этой прямой. Однако в некоторых случаях удобно рассматривать движение и вдоль оси Oy:

2.1.7 График изменения координаты.

Уравнение координаты при равномерном движении имеет вид (2.5).

График изменения координаты при равномерном движении — это прямая линия.

Направление движения: если с течением времени координата увеличивается (прямая поднимается вверх), то тело движется по направлению оси Ox (прямые 1 и 2); если координата уменьшается (прямая опускается вниз), то движение происходит против оси Ox.

Значение скорости: чем больше тангенс угла наклона (чем круче поднимается вверх или опускает вниз), тем больше модуль скорости; где — изменение координаты за время

Начальная координата тел — точка пересечения прямой с вертикальной осью (на рисунке это ось Ox, но мы привыкли, что вертикальная ось — ось Ox).

Время и место встречи двух тел — точка пересечения графиков координат двух тел; из точки пересечения следует опустить перпендикуляры на ось времени и ось координат.

Пересечение прямой с осью времени — точка пересечения прямой с ось времени означает, что тело проехало мимо начала отсчета.

2.2 Средняя скорость неравномерного движения.

2.2.1 Неравномерное движение — это движение с переменной скоростью. Скорость со временем может меняться как угодно — по любому закону.

2.2.2 Средняя векторная скорость.

где — перемещение за время t.

2.2.3 Средняя путевая (скалярная) скорость.

где L — весь путь, пройденный за время t.

2.3 Относительность механического движения.

В определении системы отсчета было сказано, что за тело отсчета можно выбирать абсолютно любое тело. В зависимости от выбора такого тела, то есть от выбора системы отсчета, одно и то же движение будет выглядеть по-разному. Например, сидим в движущейся машине — относительно машины мы неподвижны, относительно земли — движемся. Покой относителен. Движение тела относительно и положение тела относительно.

2.3.1 Правило сложения перемещений.

Векторная сумма перемещений

где — перемещение относительно неподвижной системы отсчета (НСО), — перемещение относительно подвижной системы отсчета (ПСО), — перемещение самой подвижной системы отсчета (СПСО).

2.3.2 Правило сложения скоростей.

Векторная сумма скоростей

где — скорость относительно неподвижной системы отсчета (НСО), — скорость относительно подвижной системы отсчета (ПСО), — перемещение самой подвижной системы отсчета (СПСО).

2.3.3 Относительная скорость.

Векторная разность скоростей

где — скорость первого тела относительно второго (относительная скорость), — скорость первого тела, — скорость второго тела.

Источник