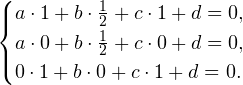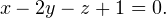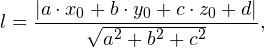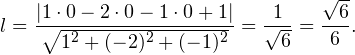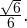что такое расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми – определение и примеры нахождения.
В этой статье внимание нацелено на нахождение расстояния между скрещивающимися прямыми методом координат. Сначала дано определение расстояния между скрещивающимися прямыми. Далее получен алгоритм, позволяющий найти расстояние между скрещивающимися прямыми. В заключении детально разобрано решение примера.
Навигация по странице.
Расстояние между скрещивающимися прямыми – определение.
Прежде чем дать определение расстояния между скрещивающимися прямыми, напомним определение скрещивающихся прямых и докажем теорему, связанную со скрещивающимися прямыми.
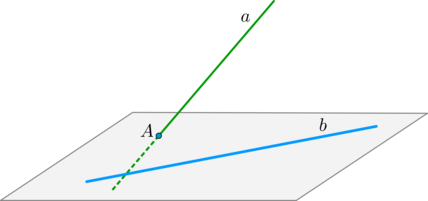
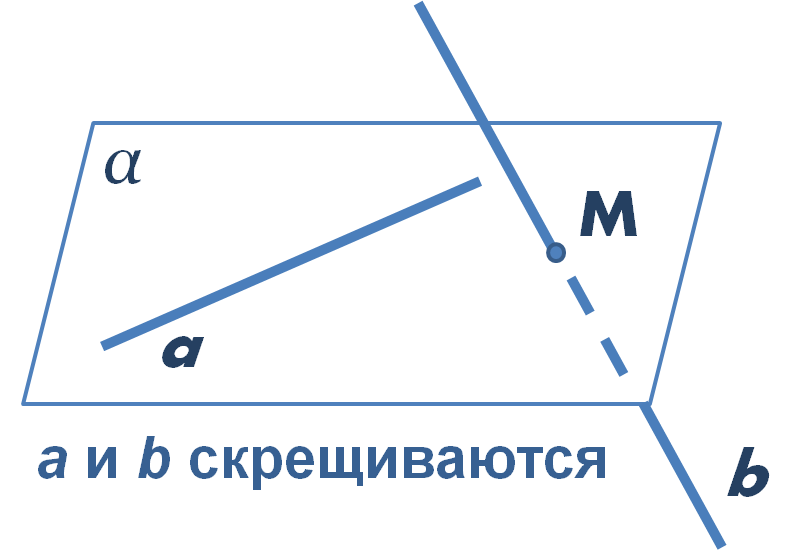
В разделе взаимное расположение прямых в пространстве мы упоминали, что две прямые называются скрещивающимися, если они не лежат в одной плоскости.
Через каждую из скрещивающихся прямых проходит единственная плоскость, которой параллельна другая прямая.
В разделе способы задания плоскости мы упоминали, что через две пересекающиеся прямые проходит единственная плоскость (что следует из аксиомы о плоскости, проходящей через три различные точки, не лежащие на одной прямой). Следовательно, через пересекающиеся прямые b и a1 проходит единственная плоскость. Обозначим ее 
Единственность плоскости 
Теперь можно переходить непосредственно к определению расстояния между скрещивающимися прямыми. Определение расстояния между скрещивающимися прямыми дается через расстояние между прямой и параллельной ей плоскостью.
Расстояние между скрещивающимися прямыми – это расстояние между одной из скрещивающихся прямых и параллельной ей плоскостью, проходящей через другую прямую.
В свою очередь расстояние между прямой и параллельной ей плоскостью есть расстояние от некоторой точки прямой до плоскости. Тогда справедлива следующая формулировка определения расстояния между скрещивающимися прямыми.
Расстояние между скрещивающимися прямыми – это расстояние от некоторой точки одной из скрещивающихся прямых до плоскости, проходящей через другую прямую параллельно первой прямой.
Нахождение расстояния между скрещивающимися прямыми – теория, примеры, решения.
При нахождении расстояния между скрещивающимися прямыми основная сложность часто заключается в том, чтобы увидеть или построить отрезок, длина которого равна искомому расстоянию. Если такой отрезок построен, то в зависимости от условий задачи его длина может быть найдена с помощью теоремы Пифагора, признаков равенства или подобия треугольников и т.п. Так мы и поступаем при нахождении расстояния между скрещивающимися прямыми на уроках геометрии в 10-11 классах.
С определением координат точки М1 сложностей не возникает, если хорошо знать основные виды уравнений прямой в пространстве. А вот на получении уравнения плоскости 
Осталось получить координаты нормального вектора плоскости 
Итак, мы имеем общее уравнение плоскости 

Остается только привести общее уравнение плоскости к нормальному виду 

Таким образом, чтобы найти расстояние между скрещивающимися прямыми a и b нужно:
Разберем решение примера.
Очевидно, прямая a проходит через точку 



Вычислим векторное произведение векторов 

Тогда уравнение плоскости 


Нормирующий множитель для общего уравнения плоскости 


Осталось воспользоваться формулой для вычисления расстояния от точки 

Это и есть искомое расстояние между заданными скрещивающимися прямыми.
Нахождение расстояния между скрещивающимися прямыми
\(\blacktriangleright\) Скрещивающиеся прямые – это прямые, через которые нельзя провести одну плоскость.
Признак скрещивающихся прямых: если первая прямая пересекает плоскость, в которой лежит вторая прямая, в точке, не лежащей на второй прямой, то такие прямые скрещиваются.
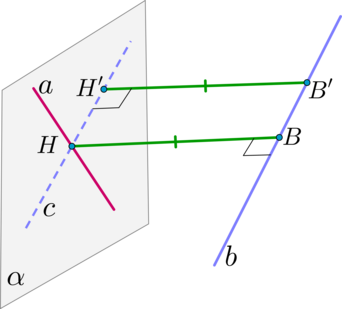
\(\blacktriangleright\) Т.к. через одну из скрещивающихся прямых проходит ровно одна плоскость, параллельная другой прямой, то расстояние между скрещивающимися прямыми — это расстояние между одной из этих прямых и плоскостью, проходящей через вторую прямую параллельно первой.
Таким образом, если прямые \(a\) и \(b\) скрещиваются, то:
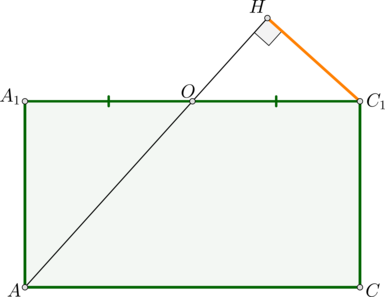
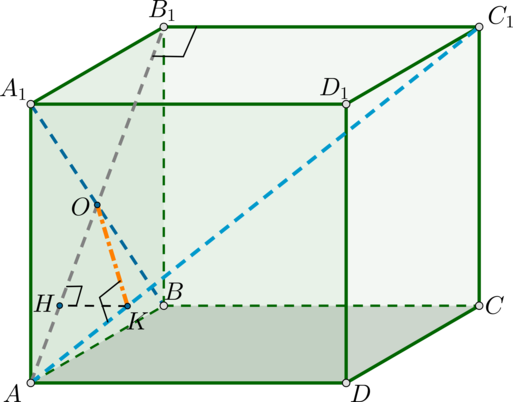
Шаг 2. Из точки пересечения прямых \(a\) и \(c\) ( \(a\cap c=H\) ) опустить перпендикуляр \(HB\) на прямую \(b\) (первый способ).
Или из любой точки \(B’\) прямой \(b\) опустить перпендикуляр на прямую \(c\) (второй способ).
В зависимости от условия задачи какой-то из этих двух способов может быть гораздо удобнее другого.
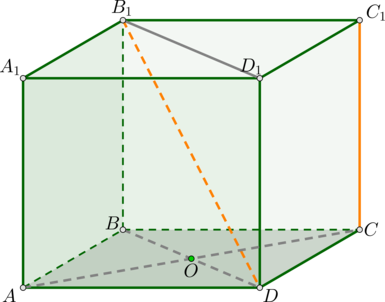
По теореме Пифагора из \(\triangle AA_1O\) : \[AO=\sqrt
Следовательно, из \((*)\) теперь можно найти перпендикуляр
Заметим, что \(\triangle AOK\sim \triangle AC_1B_1\) (по двум углам). Следовательно,
Расстояние между скрещивающимися прямыми.
Описание презентации по отдельным слайдам:
Существует три способа определения расстояния между скрещивающимися прямыми Расстояние между скрещивающимися прямыми равно длине перпендикуляра, опущенного из: 1) любой точки одной из прямых на плоскость, проходящую через другую прямую, параллельно первой прямой а b α h 2) любой точки плоскости, проходящей через одну из прямых на параллельную ей плоскость, проходящую через другую прямую. b а α β h 3) точки пересечения одной из прямых с перпендикулярной ей плоскостью на другую прямую, лежащую в этой плоскости. h a b α O Рассмотрим каждый из этих способов отдельно
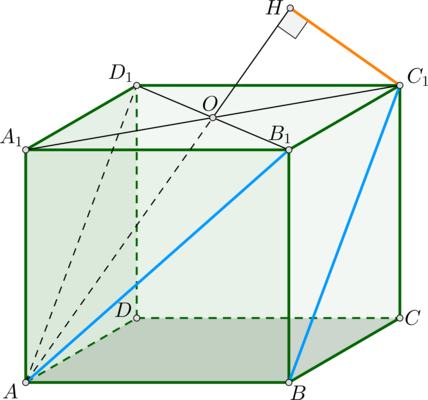
Расстояние между скрещивающимися прямыми равно длине перпендикуляра, опущенного из любой точки одной из прямых на плоскость, проходящую через другую прямую, параллельно первой прямой Чтобы найти расстояние между ними надо: 1.Провести плоскость α через прямую а параллельно прямой b 2.Из любой точки прямой b опустить перпендикуляр на прямую а Даны две скрещивающиеся прямые а и b Пример: построить общий перпендикуляр к диагонали В1D прямоугольного параллелепипеда ABCDA1B1C1D1 и боковому ребру С1С b a h α h- искомое расстояние А В С D A1 B1 C1 D1 F Построить плоскость, содержащую прямую В1D и параллельную прямой С1С * 2. Из точки С прямой С1С опустить перпендикуляр СF на плоскость ВВ1D1D. 1-ый способ h
2-ой способ Расстояние между скрещивающимися прямыми равно длине перпендикуляра опущенного из любой точки плоскости, проходящей через одну из прямых на параллельную ей плоскость, проходящую через другую прямую. Даны две скрещивающиеся прямые а и b α β а b h Для того, чтобы найти расстояние между ними надо: 1.Построить плоскости α ║ β, содержащие прямые а и b соответственно. 2.Из любой точки плоскости α опустить перпендикуляр h на плоскость β Пример: Найти расстояние между двумя диаметрами верхнего и нижнего оснований цилиндра h Так как диаметры лежат в параллельных плоскостях (основания цилиндра параллельны).то расстоянием между этими диаметрами является образующая цилиндра, так как она перпендикулярна обоим основаниям. d1 d2 h – искомое расстояние
Расстояние между скрещивающимися прямыми равно длине перпендикуляра, опущенному из точки пересечения одной из прямых с перпендикулярной ей плоскостью на другую прямую, лежащую в этой плоскости. Даны две скрещивающиеся прямые а и b Чтобы найти расстояние между ними надо: 1.Построить плоскость α, содержащую прямую b и перпендикулярную прямой а (прямая а пересекает плоскость α в точке О) 2.Из точки О опустить перпендикуляр h на прямую b. Пример: Найти расстояние между ребром основания ВС куба и диагональю АВ1 смежной боковой грани (диагональ не пересекает это ребро). а b О α h h – искомое расстояние 3 – ий способ В1 С1 D1 A1 B C D A 1. Плоскость АА1В1В перпендикулярна прямой ВС и содержит прямую АВ1. Значит, именно из точки В – точки пересечения прямой ВС и плоскости АА1В1В – надо опустить перпендикуляр h на прямую АВ1 h
Курс повышения квалификации
Охрана труда
Курс профессиональной переподготовки
Библиотечно-библиографические и информационные знания в педагогическом процессе
Курс профессиональной переподготовки
Охрана труда
Ищем педагогов в команду «Инфоурок»
Номер материала: ДВ-361778
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года
Время чтения: 1 минута
Минпросвещения РФ опубликовало методические рекомендации по проведению инклюзивных смен для детей с ОВЗ
Время чтения: 2 минуты
ФИПИ опубликовал демоверсии ОГЭ и ЕГЭ 2022
Время чтения: 1 минута
В Псковской области ввели обязательную вакцинацию для студентов
Время чтения: 1 минута
На новом «Уроке цифры» школьникам расскажут о разработке игр
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Расстояние между скрещивающимися прямыми
Описание презентации по отдельным слайдам:
РАССТОЯНИЕ МЕЖДУ СКРЕЩИВАЮЩИМИСЯ ПРЯМЫМИ Координатным и векторным способом Алферова Наталья Васильевна, учитель математики МКОУ «Горячеключевская СОШ» Омского района Омской области
Основные понятия Расстоянием между скрещивающимися прямыми называется длина общего перпендикуляра к данным прямым Расстоянием между скрещивающимися прямыми называется расстояние от точки одной прямой до плоскости параллельной данной прямой и содержащей вторую прямую.
В правильной треугольной призме АВСА1В1С1, все ребра которой равны 1, найдите расстояние между прямыми АВ и СВ1 z y x Рассмотрим плоскость (А1В1С), содержащую прямую В1С и параллельную прямой АВ. Расстоянием между скрещивающимися прямыми будет расстояние от точки прямой АВ, например от А, до плоскости (А1В1С). Введём прямоугольную систему координат ОХУZ так, чтобы ось ОХ была параллельна высоте ВН основания, ось ОУ совпадала с АС, ось ОZ совпадала с АА1. Н
M K A= (- 1/3)D, B=(1/3)D, C=(-1/4)D. Уравнение плоскости (МКD): (-1/3)Dx+(1/3)Dy+(-1/4)Dz+D=0, (-1/3)x+(1/3)y+(-1/4)z+1=0. Определим расстояние от точки В(0;3;0) до плоскости (МКD) по формуле d= d=|1+1|/√1/9+1/9+1/16=√41/12 Ответ: √41/12 z x y Спасибо за внимание.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Ищем педагогов в команду «Инфоурок»
Номер материала: 282855
Не нашли то что искали?
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Безлимитный доступ к занятиям с онлайн-репетиторами
Выгоднее, чем оплачивать каждое занятие отдельно
ФИПИ опубликовал демоверсии ОГЭ и ЕГЭ 2022
Время чтения: 1 минута
В Якутии школьников отправили на дистанционку из-за морозов
Время чтения: 1 минута
Минпросвещения разрабатывает образовательный минимум для подготовки педагогов
Время чтения: 2 минуты
На новом «Уроке цифры» школьникам расскажут о разработке игр
Время чтения: 1 минута
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Российские школьники установили рекорд на олимпиаде по астрономии
Время чтения: 2 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Расстояние между двумя скрещивающимися прямыми
В данной статье на примере решения задачи C2 из ЕГЭ разобран способ нахождения расстояния между скрещивающимися прямыми с помощью метода координат. Напомним, что прямые являются скрещивающи-мися, если они не лежат в одной плоскости. В частности, если одна прямая лежит в плоскости, а вторая прямая пересекает эту плоскость в точке, которая не лежит на первой прямой, то такие прямые являются скрещивающимися (см. рисунок).
Для нахождения расстояния между скрещивающимися прямыми необходимо:
Разберем данный алгоритм подробнее на примере решения задачи C2 из ЕГЭ по математике.
Расстояние между прямыми в пространстве
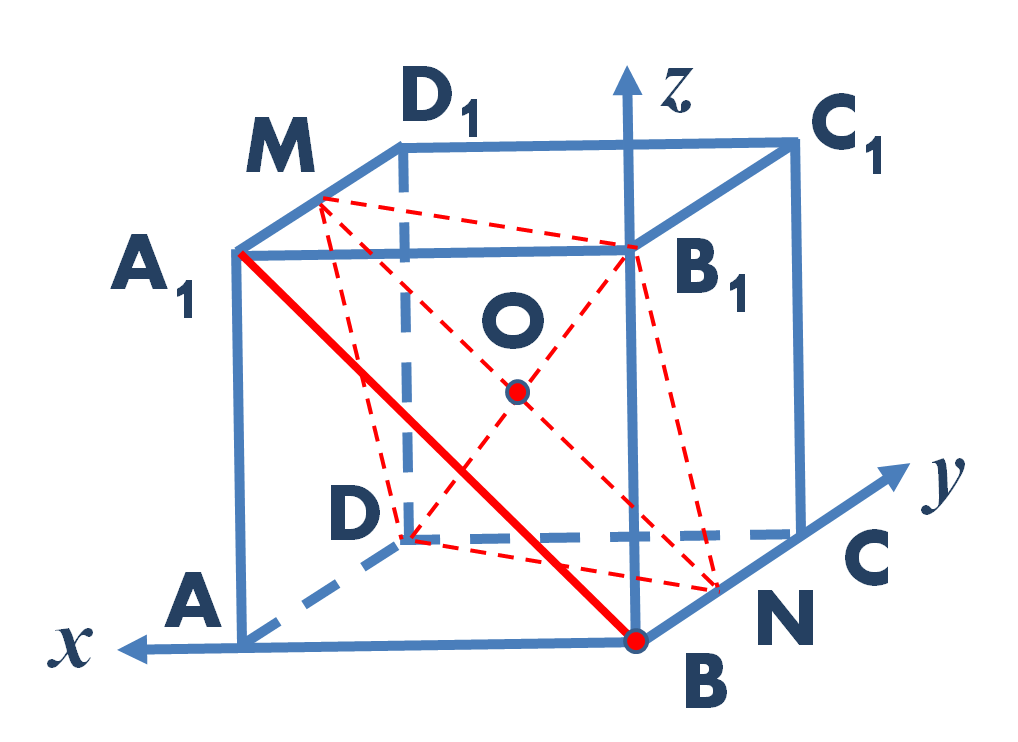
Рис. 1. Чертеж к задаче
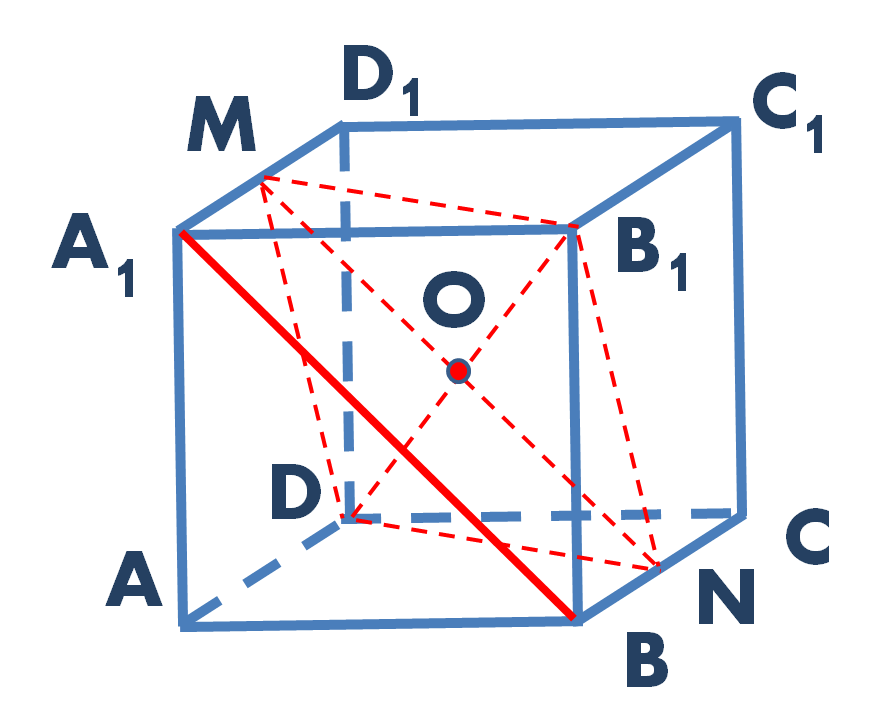
Решение. Через середину диагонали куба DB1 (точку O) проведем прямую, параллельную прямой A1B. Точки пересечения данной прямой с ребрами BC и A1D1 обозначаем соответственно N и M. Прямая MN лежит в плоскости MNB1 и параллельна прямой A1B, которая в этой плоскости не лежит. Это означает, что прямая A1B параллельна плоскости MNB1 по признаку параллельности прямой и плоскости (рис. 2).
Рис. 2. Искомое расстояние между скрещивающимися прямыми равно расстоянию от любой точки выделенной прямой до изображенной плоскости
Ищем теперь расстояние от какой-нибудь точки прямой A1B до плоскости MNB1. Это расстояние по определению будет являться искомым расстоянием между скрещивающимися прямыми.
Для нахождения этого расстояния воспользуемся методом координат. Введем прямоугольную декартову систему координат таким образом, чтобы ее начало совпало с точкой B, ось X была направлена вдоль ребра BA, ось Y — вдоль ребра BC, ось Z — вдоль ребра BB1 (рис. 3).
Рис. 3. Прямоугольную декартову систему координат выберем так, как показано на рисунке
Находим уравнение плоскости MNB1 в данной системе координат. Для этого определяем сперва координаты точек M, N и B1: 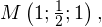
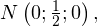
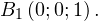
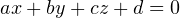
Из второго уравнения системы получаем 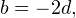
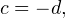
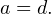
Замечаем, что 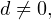
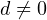
Расстояние от точки до плоскости определяется по формуле:
где 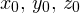
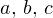
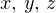
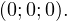
Ответ: