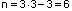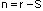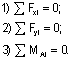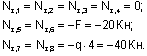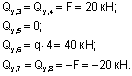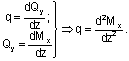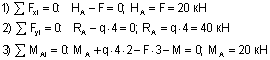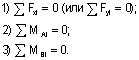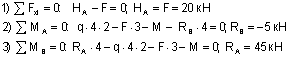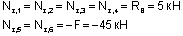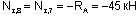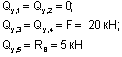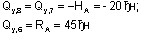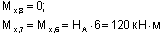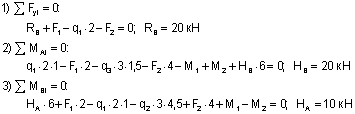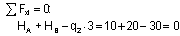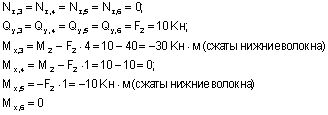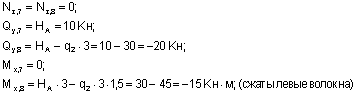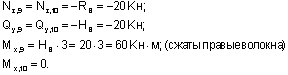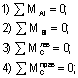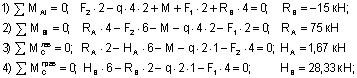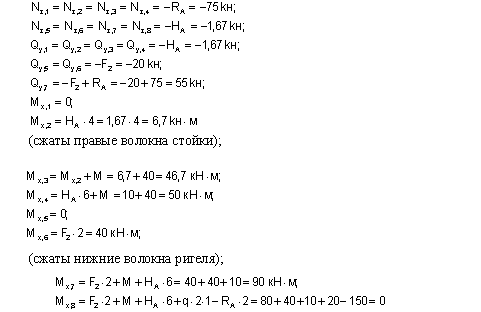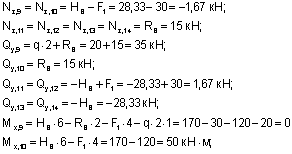что такое рама сопромат

iSopromat.ru

Рамой, в строительной механике и сопротивлении материалов, называют стержни с ломаной осью и их комбинации, которые во всех или отдельных узлах, в отличие от стержневых систем соединены не шарнирно, а жестко, не имея возможности взаимного перемещения без деформаций.

Примеры расчета рам:

Различают плоские и пространственные рамы.
В плоских рамах под действием внешних нагрузок в поперечных сечениях стержней могут возникать только продольные силы N, поперечные силы Q и изгибающие моменты M:
Пример плоской рамы

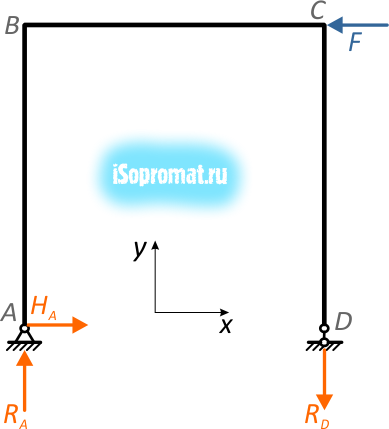
Здесь на участках:
CD — только растяжение (N);
AB и BC – сжатие + поперечный изгиб (N, Q и M).

В пространственных рамах к вышеперечисленным внутренним силовым факторам может добавляться скручивающий момент T:
Пример пространственной рамы

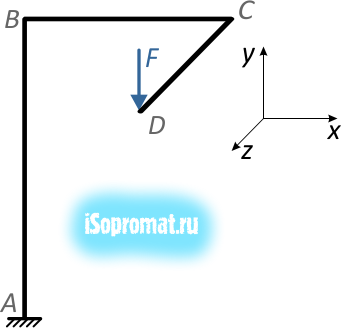
Здесь:
участок CD изгибается (Q и M);
BC – поперечный изгиб с кручением (Q, M и T);
AB – сжатие + чистый изгиб (N и M).

Как и в простых балках, для расчета внутренних усилий в рамах используется метод сечений.

Эпюры в рамах принято строить на ломаных линиях, представляющих комбинацию продольных осей, стержней, составляющих раму.

Например, для плоской рамы изображенной на рис. 1, эпюра изгибающих моментов будет иметь вид:
Эпюра изгибающих моментов для плоской рамы

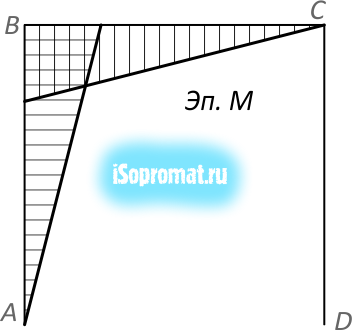
После построения эпюр их необходимо проверять.

Проверка проводится по дифференциальным зависимостям и выполняется так называемая «узловая проверка», для этого мысленно вырезаются узловые соединения стержней рамы, и рассматривается их равновесие, по данным принятым с соответствующих эпюр в окрестности рассматриваемого узла рамы.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Что такое рама сопромат

Разнообразие возможных видов рам настолько велико, что не поддается ни какому описанию, да в этом и нет необходимости. Если действующие нагрузки, геометрические параметры и жесткости элементов рамы известны, то достаточно определить, какая это рама: плоская или пространственная и какая у этой рамы степень статической неопределимости.

Затем можно переходить от заданной системы к основной, строить эпюры единичных моментов, поперечных и продольных сил, одним словом заниматься расчетом рамы одним из многочисленных методов, существующих на сегодняшний день. Но в данной статье мне хотелось бы поговорить не об этом, а о том, как можно перейти от расчетов статически неопределимых балок к расчету рам, по умолчанию являющихся статически неопределимыми конструкциями, точнее наоборот.

Расчет плоских многопролетных рам на действие вертикальной нагрузки

Вообще-то даже плоская рама для одноэтажного здания, например, состоящая из колонн, жестко связанных ригелями в рассматриваемой плоскости, не такая уж и простая, но все равно рассчитать такую раму на действие вертикальной равномерно распределенной нагрузки значительно проще, чем пространственную раму многоэтажного, многопролетного здания на различные сочетания нагрузок.

Общий подход при этом можно оставить прежним и рассматривать раму, как многопролетную неразрезную балку. Вот только, если при расчете однопролетной рамы перейти к неразрезной трехпролетной балке сравнительно легко, рассматривая вертикальные стойки рамы, как дополнительные пролеты горизонтальной балки, то при расчете многопролетной рамы следует учитывать возможное влияние промежуточных вертикальных стоек.

Расчет рам на действие горизонтальной нагрузки, основные формулы

Конечно же горизонтальные нагрузки, действующие на раму, могут быть разными: сосредоточенными и(или) распределенными, точки или места приложения горизонтальных нагрузок также могут быть разными. Однако самой распространенной из горизонтальных нагрузок для рам является ветровая нагрузка. Для упрощения расчетов такую нагрузку часто рассматривают как сосредоточенную, приложенную в одном из узлов рамы.

Если в рассматриваемой плоскости рамы не предусмотрены диафрагмы жесткости, то горизонтальная нагрузка будет передаваться на элементы рамы.

Расчет 4-х пролетной рамы с равными пролетами

При таких исходных условиях расчет рамы большой сложности не представляет, так как симметричность рамы и действующей нагрузки, а также равные длины и жесткости элементов значительно упрощают решение задачи.

Источник

Построение эпюр для плоских рам

При решении задач сопромата, плоской рамой называется стержневая система, элементы которой жестко или шарнирно соединены между собой, нагруженная в своей плоскости.

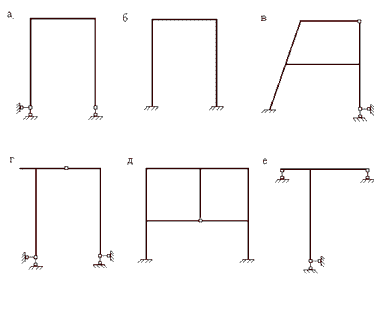
Как и многие другие системы, рамы делятся на статически определимые и статически неопределимые (рис.10, б,в,д,е).

Для определения степени статической неопределимости плоской рамы можно воспользоваться формулой:

Для рамы (рис.10,б) имеем:

Для рамы (рис.10,д):
К=3; Ш=3

В более простых случаях, когда отсутствуют замкнутые контуры и промежуточные шарниры, то есть когда используются комбинации тех же опор, что и в балках (жесткая заделка, шарнирно-подвижная и шарнирно-неподвижная опоры), для определения степени статической неопределимости используется “балочная” формула:

Ограничимся рассмотрением простейших статически определимых рам трех видов:

Из шести внутренних силовых факторов в сечениях плоской рамы в общем случае возникают три: продольная сила Nz; поперечная сила Qy; изгибающий момент Mx.

Правила знаков. Для Nz и Qy сохраняются ранее принятые правила знаков.

Nz > 0, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части, вызывает в данном сечении растяжение и Nz 0, если внешняя нагрузка, приложенная к рассматриваемой отсеченной части, стремится повернуть данное сечение по часовой стрелке и Qy Mx в балках, где в соответствии с принятым для изгибающих моментов правилом знаков (см. 1.7) ординаты эпюр Mx всегда оказывались расположенными со стороны сжатых волокон балки.

Рамы с жесткой заделкой

Пример 7.

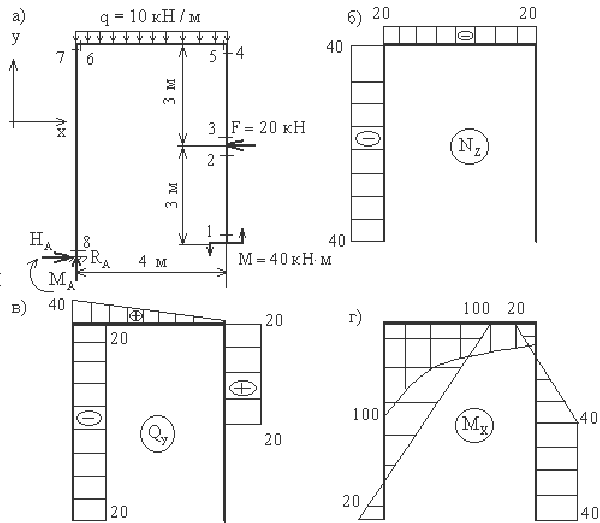
Рассмотрим жесткозащемленную плоскую раму (рис.11,а). В жесткой заделке рамы в общем случае нагружения возникают три опорные реакции: две силы (Ha и Ra ) и опорный момент (Ma). Для построения эпюр определение этих реакций не является безусловной необходимостью: расчет, как и в случае жесткозащемленной балки, можно вести от свободного конца, то есть всякий раз так выбирать отсеченную часть для рассматриваемого сечения, чтобы в нее не попадала опора с неизвестными опорными реакциями. Тем не менее, иногда целесообразно вычислить опорные реакции. Это позволяет проверить построение эпюр или облегчить их построение. Для вычисления реакций в жесткозащемленной раме используются три условия равновесия:

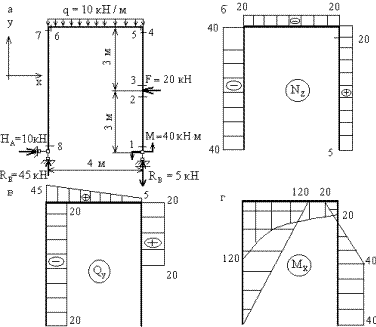
Построим эпюры Nz, Qy, Mx для рассматриваемой рамы, не вычисляя опорные реакции.

Построение эпюры Qy. Поперечная сила в любом сечении численно равна алгебраической сумме проекций всех сил, приложенных по одну сторону от рассматриваемого сечения, на поперечную ось рамы. Положение поперечной оси также будет изменяться в зависимости от принадлежности данного сечения стойкам или ригелю. С учетом правила знаков, двигаясь от свободного конца к жесткой заделке, получим для Qy:

(проекция пары М на любую ось равна нулю);

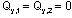
Необходимо обратить внимание на тот факт, что 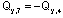, т.е. что поперечная сила в верхних сечениях противоположных стоек от действия силы, приложенной к правой стойке (при заделке, расположенной слева, и наоборот) имеет противоположные знаки. Отчасти это можно объяснить противоположными направлениями оси y для сечений 4 и 7, но более строгое обоснование указанного равенства будет дано ниже.

Построение эпюры Mx. Изгибающий момент в любом сечении численно равен алгебраической сумме моментов всех нагрузок, приложенных по одну сторону от рассматриваемого сечения, относительно этого сечения (более строго: относительно оси x этого сечения). Обратим внимание на два важных замечания:

Таким образом, для сечений 1-8 получим:

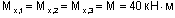
(сжатым является правое волокно в сечениях 1-3, поэтому ордината отложена вправо от оси стойки);

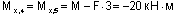
(знаки «+» и «-» здесь имеют относительный характер; результирующий момент сжимает левые волокна в сечении 4 и нижние волокна в сечении 5, поэтому ордината «20» откладывается соответственно влево и вниз);

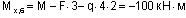
(сжаты нижние волокна);

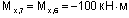
(сжаты правые волокна);

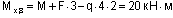
(сжаты левые волокна).

Между q, Qy и Mx в плоских рамах сохраняются те же зависимости, что и в балках, а именно:

Эпюры Nz в плоских рамах строятся наиболее просто и при отсутствии нагрузок, распределенных вдоль стержней, представляют собой графически отрезки прямых, параллельные осям стержней ( или совпадают с ними при Nz = 0).

Если проанализировать процесс построения эпюр (рис.11,б-г), то очевидно, что наиболее «сложно» вычислять ординаты в сечениях стержня, примыкающего к заделке ( на рис.11,б-г это сечения 7 и 8). Как уже отмечалось, с этой целью иногда вычисляют реакции Ha, Ra и момент Ma.

При принятом для всей рамы направлении осей x,y (рис.11,а) уравнения равновесия имеют вид:

Полученный для каждой из величин Ha, Ra, Ma знак «+» говорит, что направления их были выбраны правильно.

После вычисления опорных реакций значения величин Nz, Qy, Mx в сечениях 7 и 8 (как, впрочем, и в любом другом) можно вычислять, двигаясь от жесткой заделки к свободному концу.

Например, для сечений 7 и 8:

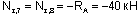
(знак «-» указывает на сжатие в этих сечениях с силой Ra);

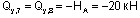
(т.к. реакция Ha стремится повернуть каждое из этих сечений против часовой стрелки.)
При сравнении величины Qy 7 с ранее полученной величиной Qy 4 видно, что

,

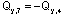
о чем уже говорилось выше.

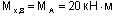
(сжаты левые волокна стойки);

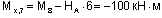
(сжаты правые волокна стойки).

Разумеется, результаты получаемые для любого сечения при движении от свободного конца к жесткой заделке и при движении в обратном направлении одинаковы.

Рамы на двух шарнирных опорах

В дальнейшем для краткости будем говорить «шарнирная рама», имея в виду ее статическую определимость и отсутствие промежуточных шарниров ( см. 1.13).

Пример 8.

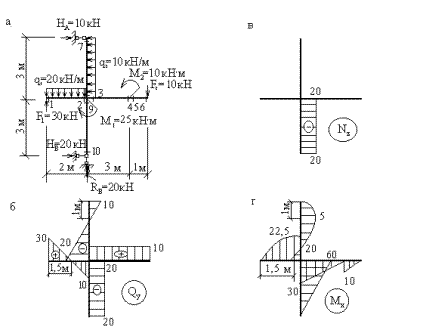
Рассмотрим раму той же конфигурации, размеров и с теми же нагрузками, что и в предыдущем примере, но с шарнирным опиранием (рис.12,а).

Здесь также имеем 8 характерных сечений, но для построения эпюр необходимо вычислить сначала опорные реакции, т.к. ни для одного из сечений нельзя выбрать отсеченную часть так, чтобы избежать попадания в нее опоры с неизвестной реакцией.

Для определения опорных реакций в плоских шарнирных рамах используются следующие уравнения равновесия:

Первое уравнение равновесия используется в том из двух приведенных вариантов, который будет содержать одну неизвестную опорную реакцию.

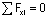
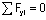
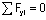
Так, в рассматриваемом примере этим условием будет которое будет содержать неизвестную реакцию Ha (в то время как условие содержало бы две неизвестных реакции). Если бы опоры располагались так, что вертикальным является один стержень, то в качестве первого шага использовалось условие .

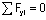
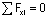
В качестве проверки вычисленных реакций используется условие, противоположное первому, то есть (или ).

Построение эпюр Nz, Qy, Mx в шарнирных рамах выполняется так же, как и в защемленных, но » с меньшими затратами», так как после вычисления реакций опор направление обхода рамы не играет роли, и выбор отсеченной части в каждом случае определяется ее простотой.

Вычислим реакции опор рамы (рис.12,а)

Знак «-«, полученный при вычислении реакции Rb, говорит, что принятое для нее направление нужно изменить на противоположное. Выполним проверку:

,
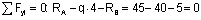
то есть реакции опор вычислены правильно.

Построение эпюры Nz.

Двигаясь по оси рамы от сечения 1 к сечению 6, получим:

Для сечений 7 и 8 проще рассматривать отсеченную часть, продвигаясь от опоры А к сечению 7:

Этот же результат получим из рассмотрения отсеченной части 1-6:

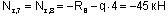
По вычисленным значениям строим эпюру Nz ( рис.12,б)

Построение эпюры Qy.

Из рассмотрения отсеченной части 1-5:

Из рассмотрения отсеченной части 8-6:

Эпюра Qy, построенная по вычисленным значениям, показана на рис.12,в.

Построение эпюры Mx.

Из рассмотрения отсеченной части 1-5:

(сжаты правые волокна стойки);

(плечо силы F равно нулю);

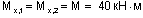
(сжаты правые волокна стойки и нижние волокна ригеля в сечениях 7 и 6 соответственно).
Эпюра Mx показана на рис12,г.

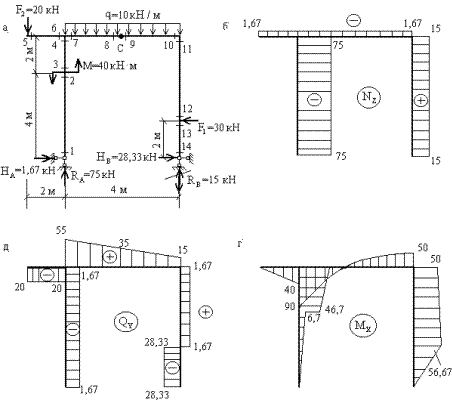
Пример 9. Рассмотрим шарнирную раму более сложной конфигурации (рис.13,а).

Уравнения статики для вычисления опорных реакций имеют вид:

Проверка вычисления опорных реакций:

При построении эпюр Nz, Qy, Mx целесообразно выбирать отсеченную часть, продвигаясь к центральному узлу рамы с четырех сторон, т.к. в этом случае определение внутренних силовых факторов в каждом из характерных сечений осуществляется наиболее просто.

Построение эпюр Nz, Qy, Mx.

Из рассмотрения левой относительно центрального узла отсеченной части (сечения 1-2):

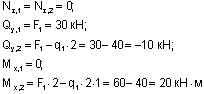
(сжаты верхние волокна).

Из рассмотрения правой отсеченной части (сечения 3-6):

Из рассмотрения верхней относительно центрального узла отсеченной части (сечения 7-8):

Из рассмотрения нижней отсеченной части (сечения 9-10):

Вычислим экстремальные значения момента Mx.
На участках под распределенной нагрузкой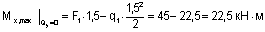
(сжаты верхние волокна).
На участке с распределенной нагрузкой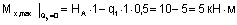
(сжаты правые волокна).

Эпюры Nz, Qy, Mx показаны на рис.13,б,в,г.

Рамы на двух опорах с промежуточным шарниром

Как отмечалось выше, рамы на двух шарнирно-неподвижных опорах с одним промежуточным шарниром также являются статически определимыми.

Пример 10. Рассмотрим построение эпюр Nz, Qy, Mx для рамы с промежуточным шарниром (рис.14,а).

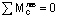
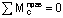
В дополнение к условиям равновесия, рассмотренным в примерах 8 и 9, здесь для определения неизвестных реакций (Ha, Ra, Hb, Rb) используются еще два условия: и , каждое из которых по своей сути выражает факт равенства нулю изгибающего момента Mx в промежуточном шарнире С (рис.14,а).

Для определения четырех неизвестных реакций возможно использование различных комбинаций уравнений равновесия, но чаще всего используются следующие уравнения:

При этом для проверки вычисленных реакций служат уравнения:

При заданных нагрузках (рис.14,а) уравнения равновесия принимают вид:

Знак «-«, полученный при вычислении реакции Rb, говорит о необходимости изменить принятое для нее направление на противоположное (перечеркнутая стрелка на рис.15,а).

Проверяем правильность вычисления опорных реакций.

Из рассмотрения левой отсеченной части:

Вновь подчеркнем, что знаки «+» и «-» для изгибающих моментов Mx принимаются относительно, то есть для разграничения противоположно направленных моментов, а эпюра Mx строится со стороны сжатых волокон.

Из рассмотрения правой отсеченной части:

(сжаты верхние волокна ригеля)

Эпюры Nz, Qy, Mx, построенные по вычисленным значениям, приведены на рис.14,б,в,г.

Источник

Расчет рамы онлайн

В данной статье, из серии о расчетах сопромата онлайн, будет посвящена рамам. Рассмотрим отличный сервис, который позволяет рассчитывать и строить эпюры: продольных и поперечных сил, а также изгибающих моментов.

rama.sopromat.org — сервис расчета рам в режиме онлайн

Рассчитать раму онлайн можно по адресу rama.sopromat.org. В основе этой программы, как и в любой современной CAE системе, лежит метод конечных элементов. Что позволяет рассчитать любую раму, какой бы сложной она не была. Также это дает возможность рассчитывать статически неопределимые системы.

Отдельно хотелось бы отметить, что этот онлайн сервис дает возможность рассчитывать системы с врезными шарнирами. Есть возможность вывода решения МКЭ.

Преимущества онлайн сервиса

Недостатки онлайн сервиса:

Несмотря на это, данный сервис, пожалуй, один из лучших по расчету рам и ферм, который есть в интернете. Лучше может быть только профессиональный софт, такой как CAE система ANSYS и ему подобные программы.

Порядок расчета рамы онлайн

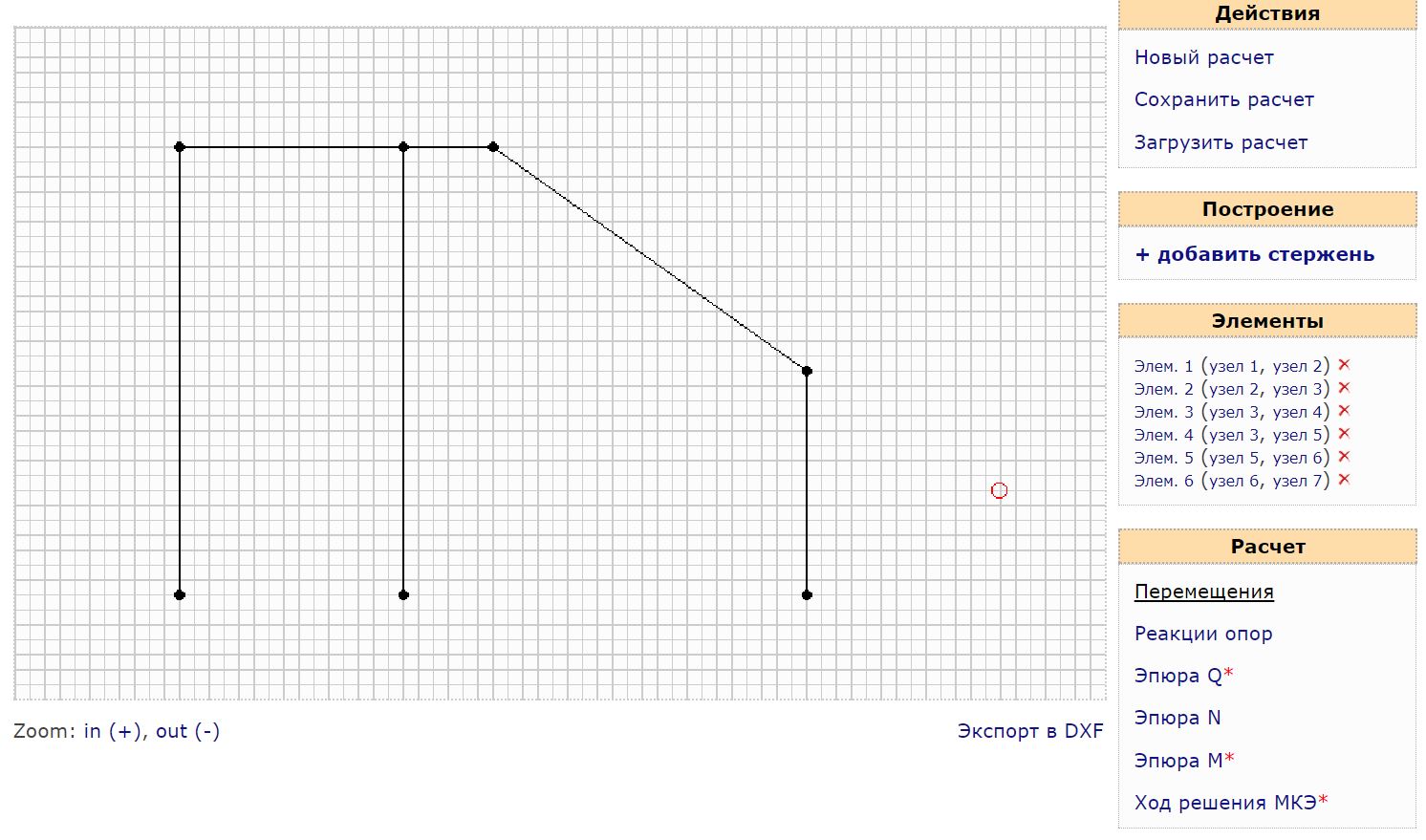
Первом делом нужно сформировать стержневую систему. Для этого на вкладке «Построение» нужно выбрать «Добавить стержень», после чего согласно своим размерам построить схему рамы:

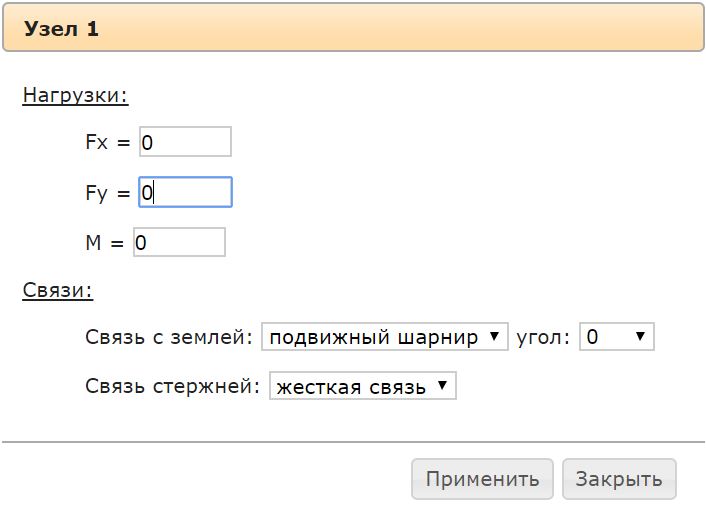
После построения расчетной схемы рамы на вкладке «Элементы» появятся все созданные стержни и узлы этих стержней. Для приложения распределенной нагрузки, нужно выбрать интересующий элемент и задать интенсивность этой нагрузки. Чтобы создать сосредоточенный момент или силу, нужно выбрать соответственно узел. Там же в узлах накладываются связи на схему: задаются опоры или жесткие связи:

После формирования расчетной схемы можно получить расчеты выбрав одну из опций на вкладке – «Расчет». Причем, реакции опор и эпюру продольных сил можно получить бесплатно. Для вывода эпюры поперечной силы и изгибающего момента, а также получения подробного хода решения методом конечных элементов нужно заплатить 20р. Вот такой удобный сервис существует для расчета рам в режиме онлайн.

Источник

Как рассчитать раму онлайн?

Автор: ssopromat · Опубликовано 24.04.2018 · Обновлено 24.04.2018

Приветствую, тебя на сайте ssopromat.ru. В этой статье поделюсь сервисами в интернете, которые в режиме онлайн позволяют рассчитать раму.

Рама – конструкция, состоящая из нескольких стержней и работающая преимущественно на изгиб. Вертикальные стержни принято называть стойками, а горизонтальные – ригелями.

Обзор сервиса

В первую очередь, хотелось бы порекомендовать старейший сервис, но очень удобный, расположенный по адресу — rama.sopromat.org

Данный расчетчик выполняет расчет по методу конечных элементов (МКЭ). Сервис позволяет рассчитать как статически определимую раму, так и неопределяемую, определить реакции опор, построить эпюры поперечных сил (Q), продольных сил (N), а также изгибающих моментов (M).

Единственным недостатком сервиса является его условная бесплатность. Бесплатно можно получить перемещение узлов (прогибы), реакции опор и эпюру продольных усилий. За все остальное нужно заплатить символическую стоимость – 20р. за день использования сервиса.

Пример работы с расчетчиком

Давайте разберем работу сервиса на конкретном примере. На вкладке «Построение» выбираем кнопку «+ добавить стержень» и формируем необходимую стержневую систему. Для первой точки системы можно выбрать любую точку рабочего пространства, затем последовательно создать стержни с учетом необходимой их длины (в левом верхнем углу рабочего пространства есть подсказка о длине создаваемого элемента).

Настройка рабочего пространства

При создании новых стержней рамы, иногда может потребоваться изменение шага ячейки рабочего пространства, для создания необходимой длины стержня. Шаг ячейки можно поменять на вкладке «Настройки»:

Выбор геометрических характеристик стержней

Геометрические характеристики стержней (момент инерции и площадь) задаются на вкладке «Для новых стержней», там же выбирается модуль упругости. Однако если вы не планируете производить расчет на жесткость и перемещения узлов вам не нужны, то эти параметры можно оставить по умолчанию.

При работе с расчетной схемой, может потребоваться ее увеличение или уменьшение. Данную операцию можно осуществить с помощью кнопок, расположенных в левом нижнем углу рабочего пространства.

После создания расчетной схемы, нужно задать для нее связи (выбрать опоры или заделку), а также приложить внешнюю нагрузку. Для этого на вкладке «Элементы», нужно выбрать интересующий узел, ранее созданной конструкции. Здесь система предложит задать нагрузку: вертикальные и горизонтальные сосредоточенные усилия, а также значение сосредоточенного момента. А также здесь выбирается тип связи для узла: жесткая связь, шарнир и подвижный шарнир. По умолчанию все узлы создаются жесткими, но можно выбрать и шарнирный узел.

Для того чтобы создать распределенную нагрузку, на вкладке «Элементы» нужно выбрать элемент (стержень). В появившемся окне задать интенсивность поперечной распределенной нагрузки или продольной. И также в этом окне можно изменить характеристики стержня: модуль упругости, момент инерции и площадь поперечного сечения.

После выполнения всех этих действий, можно получить результаты расчетов. Для этого на вкладке «Расчет», нужно выбрать интересующие результаты.

Источник