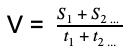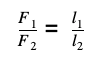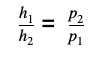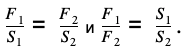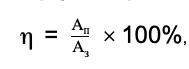что такое проверка размерности в физике

Физическая размерность

В физике разме́рность физической величины – выражение в форме степенного одночлена, составленного из произведений символов основных физических величин в различных степенях и отражающее связь данной физической величины с физическими величинами, принятыми в данной системе величин за основные и с коэффициентом пропорциональности, равным единице. Такое определение приведено в ГОСТ 16263-70 (ГСИ. Метрология. Термины и определения.), который действует и в настоящее время.

Термин размерность может относиться также к единице измерения физической величины. Часто абстрагируются от конкретных единиц измерения и описывают размерности в терминах основных физических величин, таких, например, как длина, масса и время, которые обозначают символами L, M и T, соответственно. Размерность записывают, как произведение этих символов, каждый из которых возведён в рациональную степень.

Например, размерность скорости — расстояние, делённое на время (L/T), а размерность силы — масса, умноженная на расстояние и делённая на время в квадрате (ML/T 2 ). В механике размерность любой величины может быть выражена через расстояние (которое физики часто называют «длиной»), массу и время. Электрические и магнитные величины также могут быть выражены через эти три размерности с использованием, например, закона Кулона. Однако, при использовании СИ иногда бывает удобнее ввести размерность такой основной физической величины, как электрический ток (I).

Некоторые из физических величин безразмерны в любой системе единиц, например, постоянная тонкой структуры в квантовой физике или числа Маха, Рейнольдса, Струхаля и др. в механике сред.

В СИ определены семь единиц основных физических величин, размерности которых считаются независимыми друг от друга. Поскольку система физических величин принципиально отличается от системы единиц, то в некоторых системах физических величин возможен иной перечень основных физических величин, чем в СИ.

Проверка размерности

В формулах, имеющих физический смысл, только величины, имеющие одинаковую размерность, могут складываться, вычитаться или сравниваться. Например, сложение массы какого-либо предмета с длиной другого предмета не имеет смысла. Также невозможно сказать, что больше: 1 килограмм или 3 секунды. Из этого правила, в частности, следует, что левые и правые части уравнений должны иметь одинаковую размерность.

Кроме того, аргументы экспоненциальных, логарифмических и тригонометрических функций должны быть безразмерными величинами.

Эти правила используются для проверки правильности физических формул. Если в полученном уравнении какое-то из них нарушается, то ясно, что в вычислениях была допущена ошибка.

Анализ размерности

Анализ размерности — метод, используемый физиками для построения обоснованных гипотез о взаимосвязи различных размерных параметров сложной физической системы. Иногда анализ размерности можно использовать для получения готовых формул (с точностью до безразмерной константы). Суть метода заключается в том, что из параметров, характеризующих систему, составляется выражение, имеющее нужную размерность.

При анализе размерностей формул размерность левой части уравнения должна быть равна размерности правой части уравнения. Отсутствие такого равенства говорит о неверности формулы. Однако наличие такого равенства не даёт стопроцентной гарантии верности формулы.

Источник

Анализ размерности

Читайте про метод анализа размерностей в физике: что такое анализ размерностей, пример, описание и определение, международные единицы измерения, конвертация.

Любую физическую величину можно выразить комбинацией основных физических измерений.

Задача обучения

Основные пункты

Термин

Размер – мера протяжности в определенном направлении, вроде высоты, ширины, длины, глубины.

Размеры

Размер физической величины указывает на принадлежность к одной из 7 главных величин:

[Моль] – Количество вещества.

[Cd] – Световая интенсивность.

Анализ размерности

Речь идет о проверке отношений между физическими величинами при помощи вычисления их размеров. Размер – комбинация главных физических размеров. Анализ базируется на том факте, что физический закон должен быть независимым от единиц.

Производные размеры

Подобные размеры могут включать несколько или все размеры величин. Рассмотрим метод анализа размерностей на примере силы:

Ускорение передается как [a] и выступает производной величиной соотношения скорости и времени. Скорость также выступает производной – отношение длины и времени.

Конверсия размеров

На практике встречается необходимость перевести один вид размера в другой. С часто используемыми проблем не возникает, но для некоторых нужно вычислить коэффициент преобразования:

Здесь n – количество на размеры. Далее уже можно применить коэффициент для выведения конверсии:

Источник

Размерность (физич.)

В физике разме́рность физической величины – выражение в форме степенного одночлена, составленного из произведений символов основных физических величин в различных степенях и отражающее связь данной физической величины с физическими величинами, принятыми в данной системе величин за основные и с коэффициентом пропорциональности, равным единице. Такое определение приведено в ГОСТ 16263-70 (ГСИ. Метрология. Термины и определения.), который действует и в настоящее время.

Термин размерность может относиться также к единице измерения физической величины. Часто абстрагируются от конкретных единиц измерения и описывают размерности в терминах основных физических величин, таких, например, как длина, масса и время, которые обозначают символами L, M и T, соответственно. Размерность записывают, как произведение этих символов, каждый из которых возведён в рациональную степень.

Например, размерность скорости — расстояние, делённое на время (L/T), а размерность силы — масса, умноженная на расстояние и делённая на время в квадрате (ML/T 2 ). В механике размерность любой величины может быть выражена через расстояние (которое физики часто называют «длиной»), массу и время. Электрические и магнитные величины также могут быть выражены через эти три размерности с использованием, например, закона Кулона. Однако, при использовании СИ иногда бывает удобнее ввести размерность такой основной физической величины, как электрический ток (I).

Некоторые из физических величин безразмерны в любой системе единиц, например, постоянная тонкой структуры в квантовой физике или числа Маха, Рейнольдса, Струхаля и др. в механике сред.

В СИ определены семь единиц основных физических величин, размерности которых считаются независимыми друг от друга. Поскольку система физических величин принципиально отличается от системы единиц, то в некоторых системах физических величин возможен иной перечень основных физических величин, чем в СИ.

Проверка размерности

В формулах, имеющих физический смысл, только величины, имеющие одинаковую размерность, могут складываться, вычитаться или сравниваться. Например, сложение массы какого-либо предмета с длиной другого предмета не имеет смысла. Также невозможно сказать, что больше: 1 килограмм или 3 секунды. Из этого правила, в частности, следует, что левые и правые части уравнений должны иметь одинаковую размерность.

Кроме того, аргументы экспоненциальных, логарифмических и тригонометрических функций должны быть безразмерными величинами.

Эти правила используются для проверки правильности физических формул. Если в полученном уравнении какое-то из них нарушается, то ясно, что в вычислениях была допущена ошибка.

Анализ размерности

Анализ размерности — метод, используемый физиками для построения обоснованных гипотез о взаимосвязи различных размерных параметров сложной физической системы. Иногда анализ размерности можно использовать для получения готовых формул (с точностью до безразмерной константы). Суть метода заключается в том, что из параметров, характеризующих систему, составляется выражение, имеющее нужную размерность.

При анализе размерностей формул размерность левой части уравнения должна быть равна размерности правой части уравнения. Отсутствие такого равенства говорит о неверности формулы. Однако наличие такого равенства не даёт стопроцентной гарантии верности формулы.

Источник

Содержание:

При измерении разных физических величин мы получаем их числовые значения с определенной точностью. Например, при определении размеров листа бумаги (длины, ширины) мы можем указать их с точностью до миллиметра; размеры стола – с точностью до сантиметра, размеры дома, стадиона – с точностью до метра.

Нет необходимости указывать размеры стола с точностью до миллиметра, а размеры стадиона с точностью до сантиметра или миллиметра. Мы сами в каждой ситуации, опыте и эксперименте определяем, с какой точностью нам нужны данные физические величины. Однако очень важно оценивать, насколько точно мы определяем физическую величину, какую ошибку (погрешность) в ее измерении допускаем.

При измерении мы не можем определить истинное значение измеряемой величины, а только пределы, в которых она находится.

Пример:

Измерим ширину стола рулеткой с сантиметровыми и миллиметровыми делениями на ней (рис. 5.1). Значение наименьшего деления шкалы называют ценой деления и обозначают буквой С. Видно, что цена деления рулетки С = 1 мм (или 0,1 см).

Совместим нулевое деление рулетки с краем стола и посмотрим, с каким значением
шкалы линейки совпадает второй край стола (рис. 5.1). Видно, что ширина стола составляет чуть больше 70 см и 6 мм, или 706 мм. Но результат наших измерений мы запишем с точностью до 1 мм, то есть L = 706 мм.

Абсолютная погрешность измерения ∆ (ДЕЛЬТА)

Из рис. 5.1 видно, что мы допускаем определенную погрешность и определить ее «на глаз» достаточно трудно. Эта погрешность составляет не более половины цены деления шкалы рулетки. Эту погрешность называют погрешностью измерения и помечают ∆L («дельта эль»). В данном эксперименте ее можно записать

Сам результат измерения принято записывать таким образом: ширина стола L = (706,0 ± 0,5) мм, читают: 706 плюс-минус 0,5 мм. Эти 0,5 мм в нашем примере называют абсолютной погрешностью. Значения измеряемой величины (706,0 мм) и абсолютной погрешности (0,5 мм) должны иметь одинаковое количество цифр после запятой, то есть нельзя записывать 706 мм ± 0,5 мм.

Такая запись результата измерения означает, что истинное значение измеряемой величины находится между 705,5 мм и 706,5 мм, то есть 705,5 мм ≤ L ≤ 706,5 мм.

Относительная погрешность измерения ε (ЭПСИЛОН)

Иногда важно знать, какую часть составляет наша погрешность от значения
измеряемой величины. Для этого разделим 0,5 мм на 706 мм. В результате получим: . То есть наша ошибка составляет 0,0007 долю ширины стола, или 0,0007 · 100% = 0,07%. Это свидетельствует о достаточно высокой точности измерения. Эту погрешность называют относительной и обозначают греческой буквой (эпсилон):

(5.1)

Относительная погрешность измерения свидетельствует о качестве измерения. Если длина какогото предмета равна 5 мм, а точность измерения – плюс-минус 0,5 мм, то относительная погрешность будет составлять уже 10%.

Стандартная запись результата измерений и выводы

На точность измерения влияет много факторов, в частности:

Все это необходимо учитывать при проведении измерений.

Измерительные приборы

Устройства, с помощью которых измеряют физические величины, называют измерительными приборами.

Простейший и хорошо известный вам измерительный прибор — линейка с делениями. На ее примере вы видите, что у измерительного прибора есть шкала, на которой нанесены деления, причем возле некоторых делений написано соответствующее значение физической величины. Так, значения длины в сантиметрах нанесены на линейке возле каждого десятого деления (рис. 3.11). Значения же, соответствующие «промежуточным» делениям шкалы, можно найти с помощью простого подсчета.

Разность значений физической величины, которые соответствуютближайшим делениям шкалы, называют ценой деления прибора. Ёе находят так: берут ближайшие деления, возле которых написаны значения величины, и делят разность этих значений на количество промежутков между делениями, расположенными между ними.

Например, ближайшие сантиметровые деления на линейке разделены на десять промежутков. Значит, цена деления линейки равна 0,1 см = 1 мм.

Как определяют единицы длины и времени

В старину мерами длины служили большей частью размеры человеческого тела и его частей. Дело в том, что собственное тело очень удобно как «измерительный прибор», так как оно всегда «рядом». И вдобавок «человек есть мера всех вещей»: мы считаем предмет большим или малым, сравнивая его с собой.

Так, длину куска ткани измеряли «локтями», а мелкие предметы — «дюймами» (это слово происходит от голландского слова, которое означает «большой палец»).

Однако человеческое тело в качестве измерительного прибора имеет существенный недостаток: размеры тела и его частей у разных людей заметно отличаются. Поэтому ученые решили определить единицу длины однозначно и точно. Международным соглашением было принято, что один метр равен пути, который проходит свет в вакууме за 1/299792458 с. А секунду определяют с помощью атомных часов, которые сегодня являются самыми точными.

Можно ли расстояние измерять годами

Именно так и измеряют очень большие расстояния — например, расстояния между звездами! Но при этом речь идет не о годах как промежутках времени, а о «световых годах». А один световой год — это расстояние, которое проходит свет за один земной год. По нашим земным меркам это очень большое расстояние — чтобы убедиться в этом, попробуйте выразить его в километрах! А теперь вообразите себе, что расстояние от Солнца до ближайшей к нему звезды составляет больше четырех световых лет! И по астрономическим масштабам это совсем небольшое расстояние: ведь с помощью современных телескопов астрономы тщательно изучают звезды, расстояние до которых составляет много тысяч световых лет!

Что надо знать об измерительных приборах

Приступая к измерениям, необходимо, прежде всего, подобрать приборы. Что надо знать об измерительных приборах?

На рисунке 34 изображены три линейки с одинаковыми верхними пределами (25 см). По эти линейки измеряют длину с различной точностью. Наиболее точные результаты измерений дает линейка 7, наименее точные — линейка 3. Что же такое точность измерений и от чего она зависит? Для ответа на эти вопросы рассмотрим сначала понятие цена деления шкалы прибора.

Цена деления — это значение наименьшего деления шкалы прибора.

Как определить цену деления шкалы? Для этого необходимо:

Полученное значение и будет ценой деления шкалы прибора. Обозначим ее буквой С.

Точно так же можно определить и цену деления шкалы мензурок 1 и 2 (рис. 35). Цена деления шкалы мензурки 1:

Цена деления шкалы мензурки 2:

А какими линейкой и мензуркой можно измерить точнее?

Измерим один и тот же объем мензуркой 1 и мензуркой 2. Но показаниям шкал в мензурке 1 объем воды V = 35 мл; в мензурке 2 — V = 37 мл.

Итак, любым прибором, имеющим шкалу, измерить физическую величину можно с точностью, не превышающей цены деления шкалы.

Линейкой 1 (см. рис. 34) можно измерить длину с точностью до 1 мм. Точность измерения длины линейками 2 и 3 определите самостоятельно.

Главные выводы:

Для любознательных:

В истории науки есть немало случаев, когда повышение точности измерений давало толчок к новым открытиям. Более точные измерения плотности азота, выделенного из воздуха, позволили в 1894 г. открыть новый инертный газ — аргон. Повышение точности измерений плотности воды привело к открытию в 1932 г. одной из разновидностей тяжелых атомов водорода — дейтерия. Позже дейтерий вошел в состав ядерного горючего. Оценить расстояния до звезд и создать их точные каталоги ученые смогли благодаря повышению точности при измерении положения ярких звезд на небе.

Пример решения задачи

Для измерения величины угла используют транспортир. Определите: 1) цену деления каждой шкалы транспортира, изображенного на рисунке 38; 2) значение угла BАС, используя каждую шкалу; укажите точность измерения угла ВАС в каждом случае.

Решение:

1) Цена деления нижней шкалы:

Цена деления средней шкалы:

Цена деления верхней шкалы:

2) Определенный но нижней шкале с точностью до 10° определенный по средней шкале с точностью до 5° определенный по верхней шкале с точностью до 1°

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Все формулы по физике за 7 класс

Шпаргалки по физике за 7 класс

В рамках одной статьи сложно охватить весь курс по физике, но мы осветили основные темы за 7 класс и этого достаточно, чтобы освежить знания в памяти. Скачайте и распечатайте обе шпаргалки — одна из них (подробная) пригодится для вдумчивой подготовки к ОГЭ и ЕГЭ, а вторая (краткая) послужит для решения задач.

Для тех, кто находится на домашнем обучении или вынужден самостоятельно изучать материал ввиду пропусков по болезни, рекомендуем также учебник по физике А. В. Перышкина с формулами за 7 класс и легкими, доступными пояснениями по всем темам. Он был написан несколько десятилетий назад, но до сих пор очень популярен и востребован.

Измерение физических величин

Измерением называют определение с помощью инструментов и технических средств числового значения физической величины.

Результат измерения сравнивают с неким эталоном, принятым за единицу. В итоге значением физической величины считается полученное число с указанием единиц измерения.

В курсе по физике за 7 класс изучают правила измерений с использованием приборов со шкалой. Если цена деления шкалы неизвестна, узнать ее можно с помощью следующей формулы:

ЦД = (max − min) / n, где ЦД — цена деления, max — максимальное значение шкалы, min — минимальное значение шкалы, n — количество делений между ними.

Вместо максимального и минимального можно взять любые другие значения шкалы, числовое выражение которых нам известно.

Выделяют прямое и косвенное измерение:

при прямом измерении результат можно увидеть непосредственно на шкале инструмента;

при косвенном измерении значение величины вычисляется через другую величину (например, среднюю скорость определяют на основе нескольких замеров скорости).

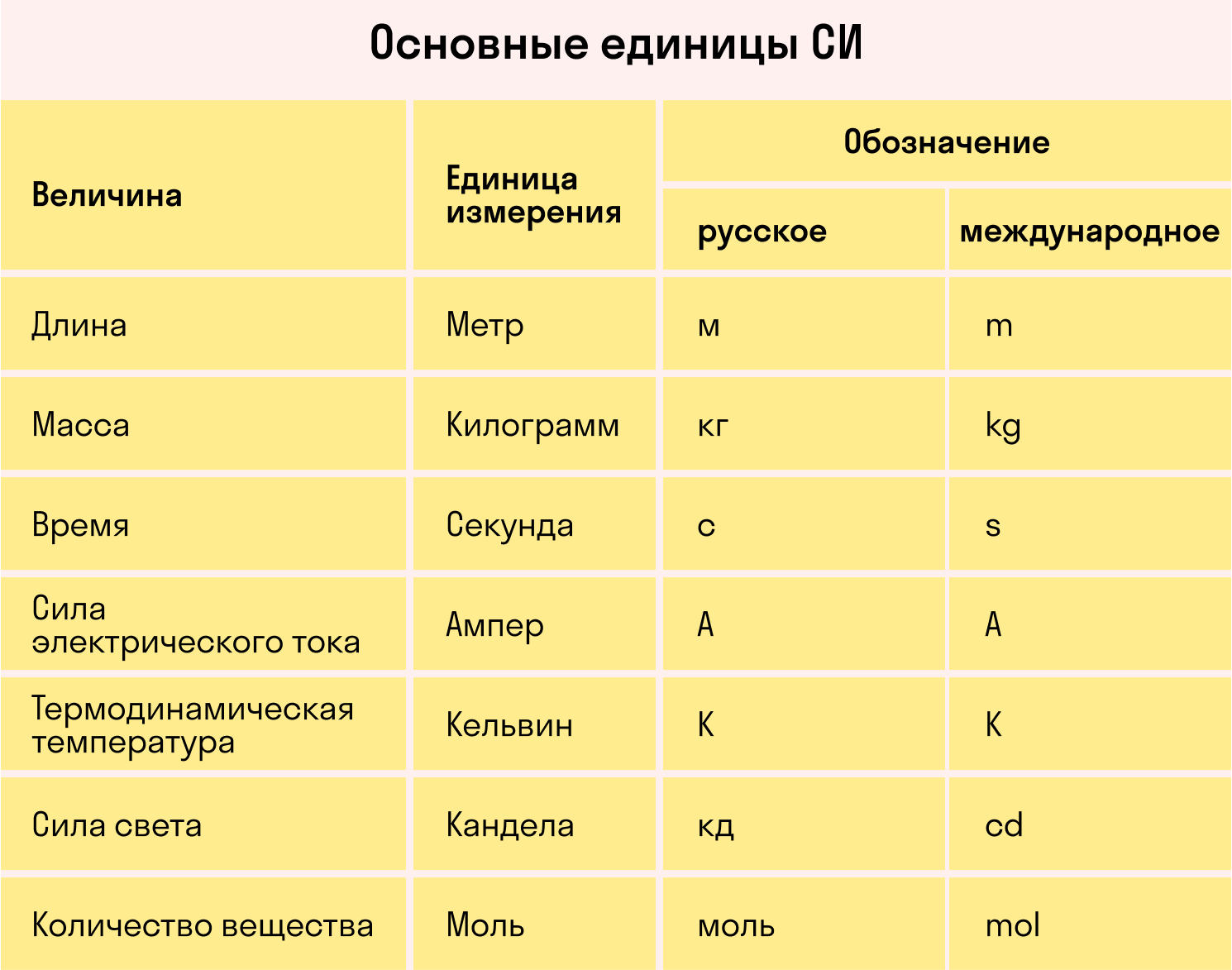
Для удобства и стандартизации измерений в 1963 году была принята Международная система единиц СИ. Она регламентирует, какие единицы измерения считать основными и использовать для формул. Обозначения этих единиц также учат в программе по физике за 7 класс.

Механическое движение: формулы за 7 класс

Механическое движение — перемещение тела в пространстве, в результате которого оно меняет свое положение относительно других тел. Закономерности такого движения изучают в рамках механики и конкретно ее раздела — кинематики.

Для того, чтобы описать движение, требуется тело отсчета, система координат, а также инструмент для измерения времени. Это составляющие системы отсчета.

Изучение механического движения в курсе по физике за 7 класс включает следующие термины:

Перемещение тела — вектор, проведенный из начальной точки в конечную.

Траектория движения — мысленная линия, вдоль которой перемещается тело.

Путь — длина траектории тела от начальной до конечной точки.

Скорость — быстрота перемещения тела или отношение пройденного им пути ко времени прохождения.

Ускорение — быстрота изменения скорости, с которой движется тело.

Равномерное прямолинейное движение означает, что тело движется вдоль прямой с одинаковой скоростью. В таком случае перемещение тела и его путь будут равны.

Формула скорости равномерного прямолинейного движения:

V = S / t, где S — путь тела, t — время, за которое этот путь пройден.

Формула скорости равномерного криволинейного движения:

где S₁ и S₂ — отрезки пути, а t₁ и t₂ — время, за которое был пройден каждый из них.

Единица измерения скорости в СИ: метр в секунду (м/с).

Формула скорости равноускоренного движения:

V = V₀ + at, где V₀— начальная скорость, а — ускорение.

Сила тяжести, вес, масса, плотность

Формулы, понятия и определения, описывающие эти физические характеристики, изучают в 7 классе в рамках такого раздела физики, как динамика.

Вес тела или вещества — это векторная величина, которая характеризует, с какой силой оно действует на горизонтальную поверхность или вертикальный подвес. Не следует путать эту величину с массой, которая является скалярной величиной.

Вес тела измеряется в ньютонах, масса тела — в граммах и килограммах.

Формула веса:

P = mg, где m — масса тела, g — ускорение свободного падения.

Ускорение свободного падения возникает под действием силы тяжести, которой подвержены все находящиеся на нашей планете тела.

g = 9,806 65 м/с 2 или 9,8 Н/кг

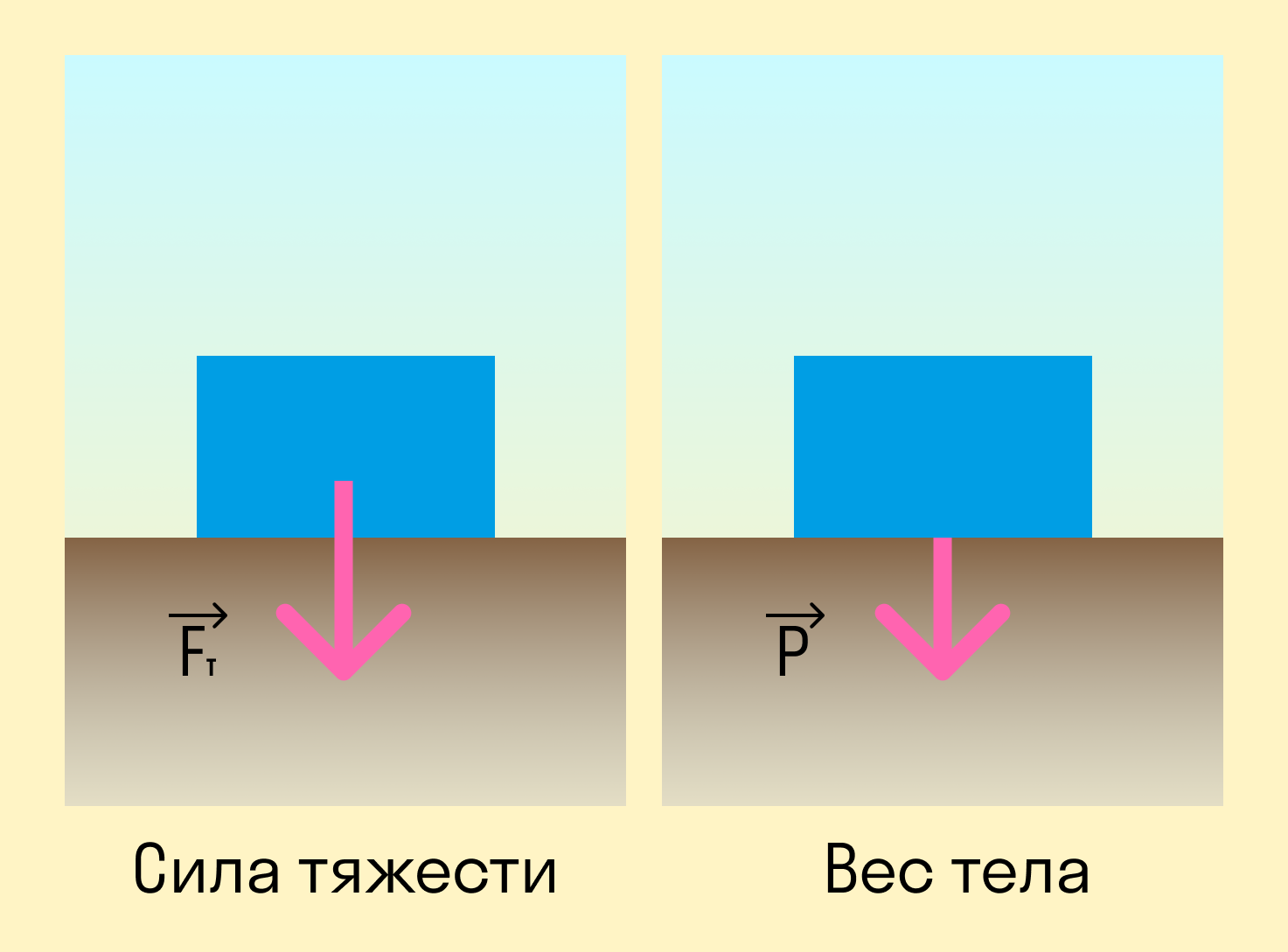
Если тело находится в покое или в прямолинейном равномерном движении, его вес равен силе тяжести.

Но эти понятия нельзя отождествлять: сила тяжести действует на тело ввиду наличия гравитации, в то время как вес — это сила, с которой само тело действует на поверхность.

Формула плотности:

ρ = m / V, где m — масса тела или вещества, V — занимаемый объем.

Механический рычаг, момент силы

О механическом рычаге говорил еще Архимед, когда обещал перевернуть Землю, если только найдется подходящая точка опоры. Это простой механизм, который помогает поднимать грузы, закрепленные на одном его конце, прилагая силу к другому концу. При этом вес груза намного превосходит прилагаемое усилие. В 7 классе физические формулы, описывающие этот процесс, изучаются в том же разделе динамики.

Рычаг — это некое твердое тело, способное вращаться вокруг неподвижной точки опоры, на один конец которого действует сила, а на другом находится груз.

Перпендикуляр, проведенный от точки опоры до линии действия силы, называется плечом силы.

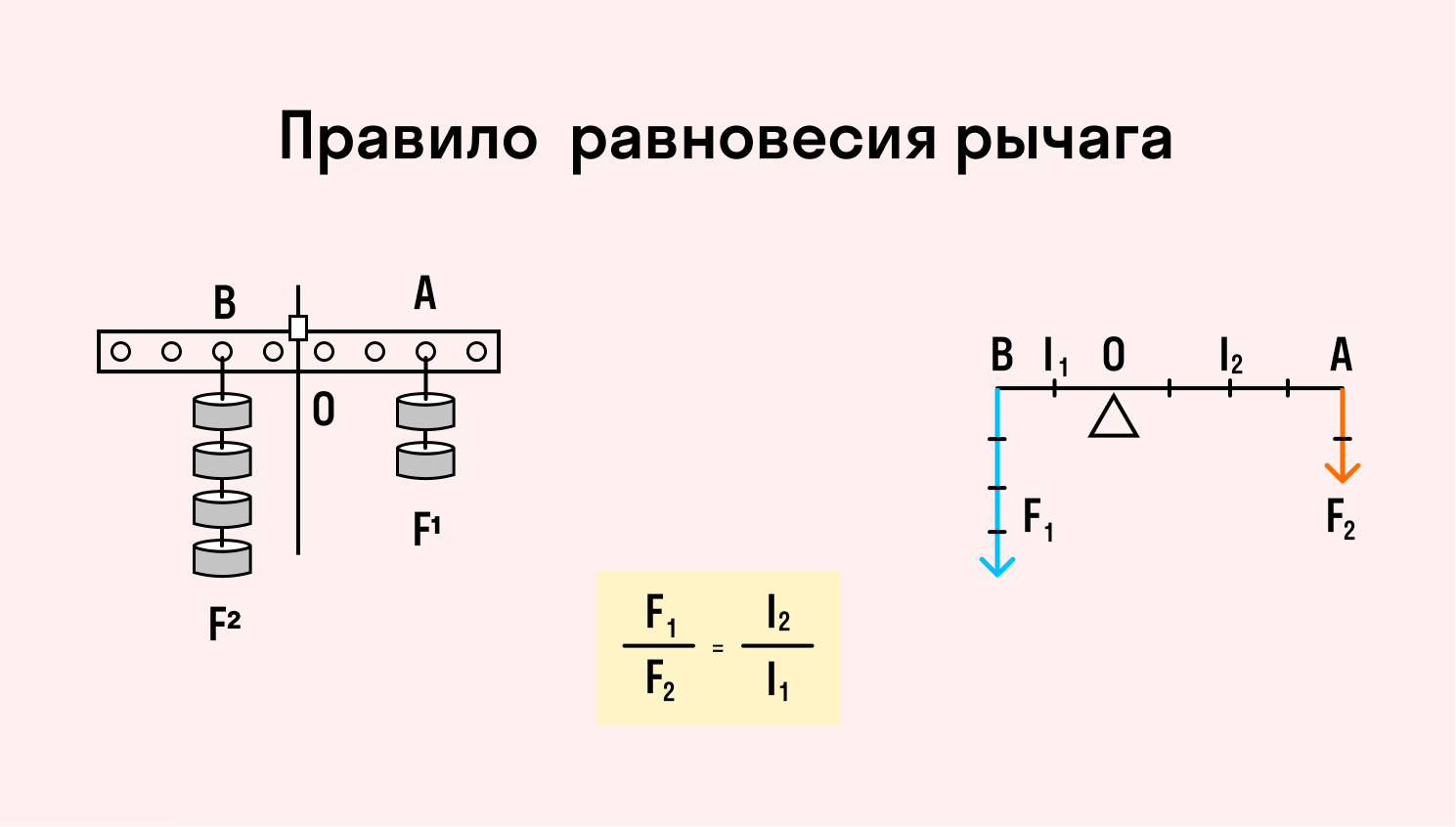
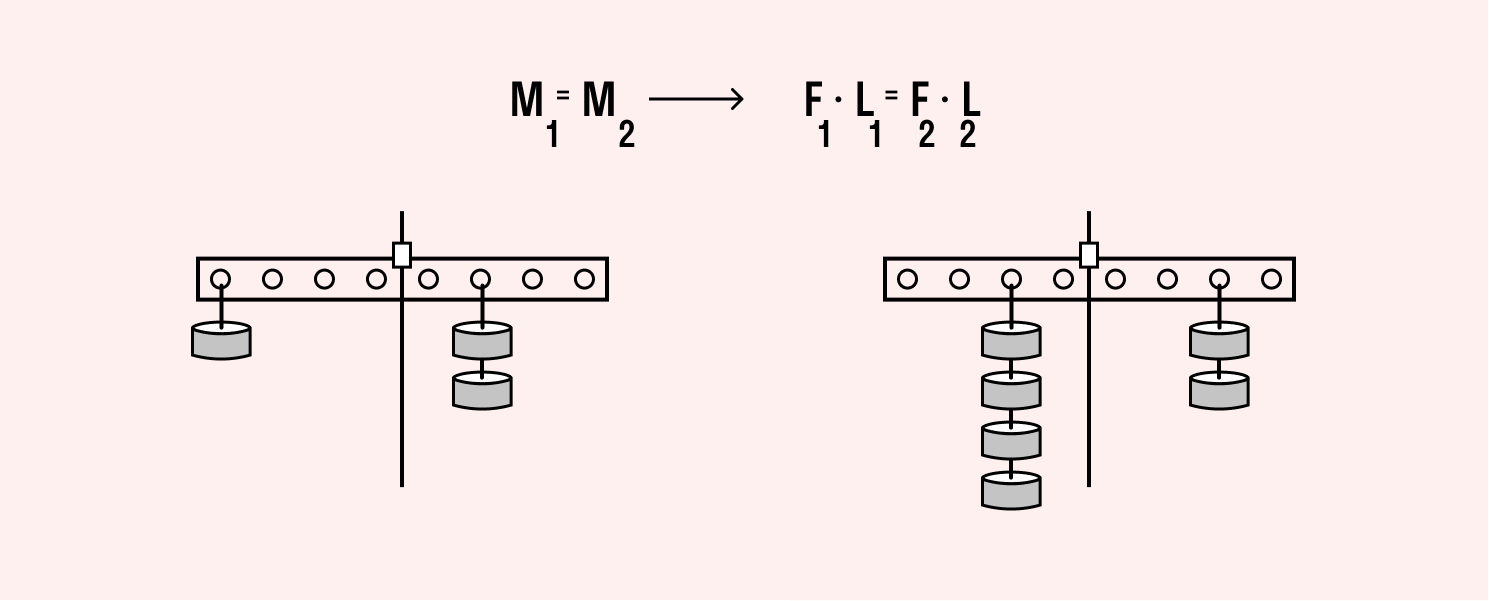
Рычаг находится в равновесии, если произведение силы на плечо с одной его стороны равно произведению силы на плечо с другой стороны.

Уравнение равновесия рычага:

Из этого следует, что рычаг уравновешен, когда модули приложенных к его концам сил обратно пропорциональны плечам этих сил.

Момент силы — это векторная величина, числовую характеристику которой можно описать как произведение модуля силы на плечо.

M = F × l, где F — модуль силы, l — длина плеча.

Единица измерения момента силы в СИ: ньютон-метр (Н·м).

Эта формула верна, если сила приложена перпендикулярно оси рычага. Если же она прилагается под углом, такой случай выходит за рамки курса физики за 7 класс и подробно изучается в 9 классе.

Правило моментов: рычаг уравновешен, если сумма всех моментов сил, которые поворачивают его по часовой стрелке, равна сумме всех моментов сил, которые поворачивают его в обратном направлении.

Можно сказать иначе: рычаг в равновесии, если сумма моментов всех приложенных к нему сил относительно любой оси равна нулю.

Давление, сила давления

Прилагая одну и ту же силу к предмету, можно получить разный результат в зависимости от того, на какую площадь эта сила распределена. Объясняют этот феномен в программе 7 класса физические термины «давление» и «сила давления».

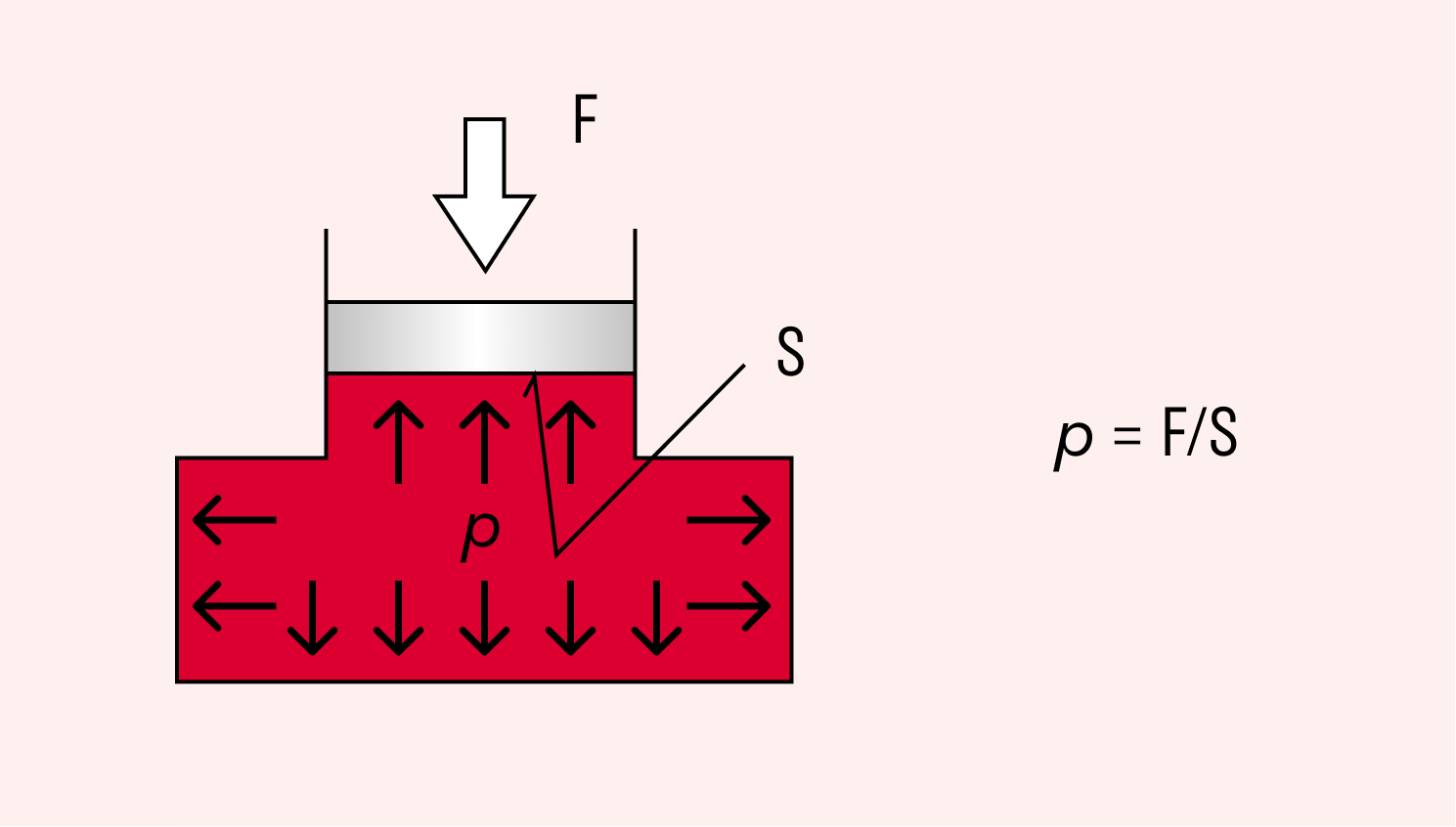
Давление — это величина, равная отношению силы, действующей на поверхность, к площади этой поверхности.

Сила давления направлена перпендикулярно поверхности.

Формула давления:

p = F / S, где F — модуль силы, S — площадь поверхности.

Единица измерения давления в СИ: паскаль (Па).

Понятно, что при одной и той же силе воздействия более высокое давление испытает та поверхность, площадь которой меньше.

Формулу для расчета силы давления вывести несложно:

В задачах по физике за 7 класс сила давления, как правило, равна весу тела.

Давление газов и жидкостей

Жидкости и газы, заполняющие сосуд, давят на его стенки. Это давление зависит от высоты столба данного вещества и от его плотности.

Формула гидростатического давления:

р = ρ × g × h, где ρ — плотность вещества, g — сила тяжести, h — высота столба.

Единица измерения давления жидкости или газа в СИ: паскаль (Па).

Однородная жидкость или газ давит на стенки сосуда равномерно, поскольку это давление создают хаотично движущиеся молекулы. И внешнее давление, оказываемое на вещество, тоже равномерно распределяется по всему его объему.

Закон Паскаля: давление, производимое на поверхность жидкого или газообразного вещества, одинаково передается в любую его точку независимо от направления.

Внешнее давление, оказываемое на жидкость или газ, рассчитывается по формуле:

p = F / S, где F — модуль силы, S — площадь поверхности.

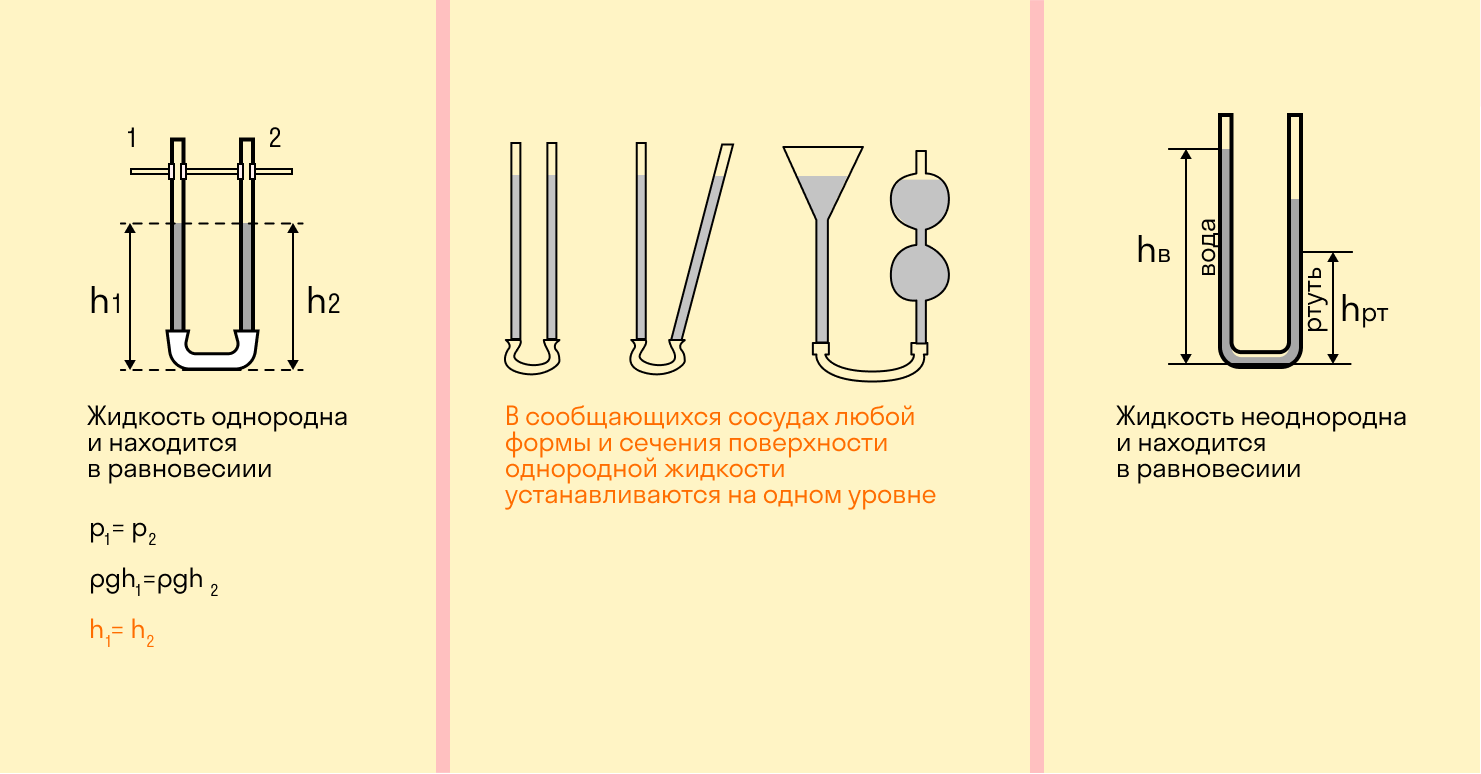
Сообщающиеся сосуды

Сообщающимися называются сосуды, которые имеют общее дно либо соединены трубкой. Уровень однородной жидкости в таких сосудах всегда одинаков, независимо от их формы и сечения.

p — плотность жидкости,

h — высота столба жидкости,

Если жидкость в сообщающихся сосудах неоднородна, т. е. имеет разную плотность, высота столба в сосуде с более плотной жидкостью будет пропорционально меньше.

Высоты столбов жидкостей с разной плотностью обратно пропорциональны плотностям.

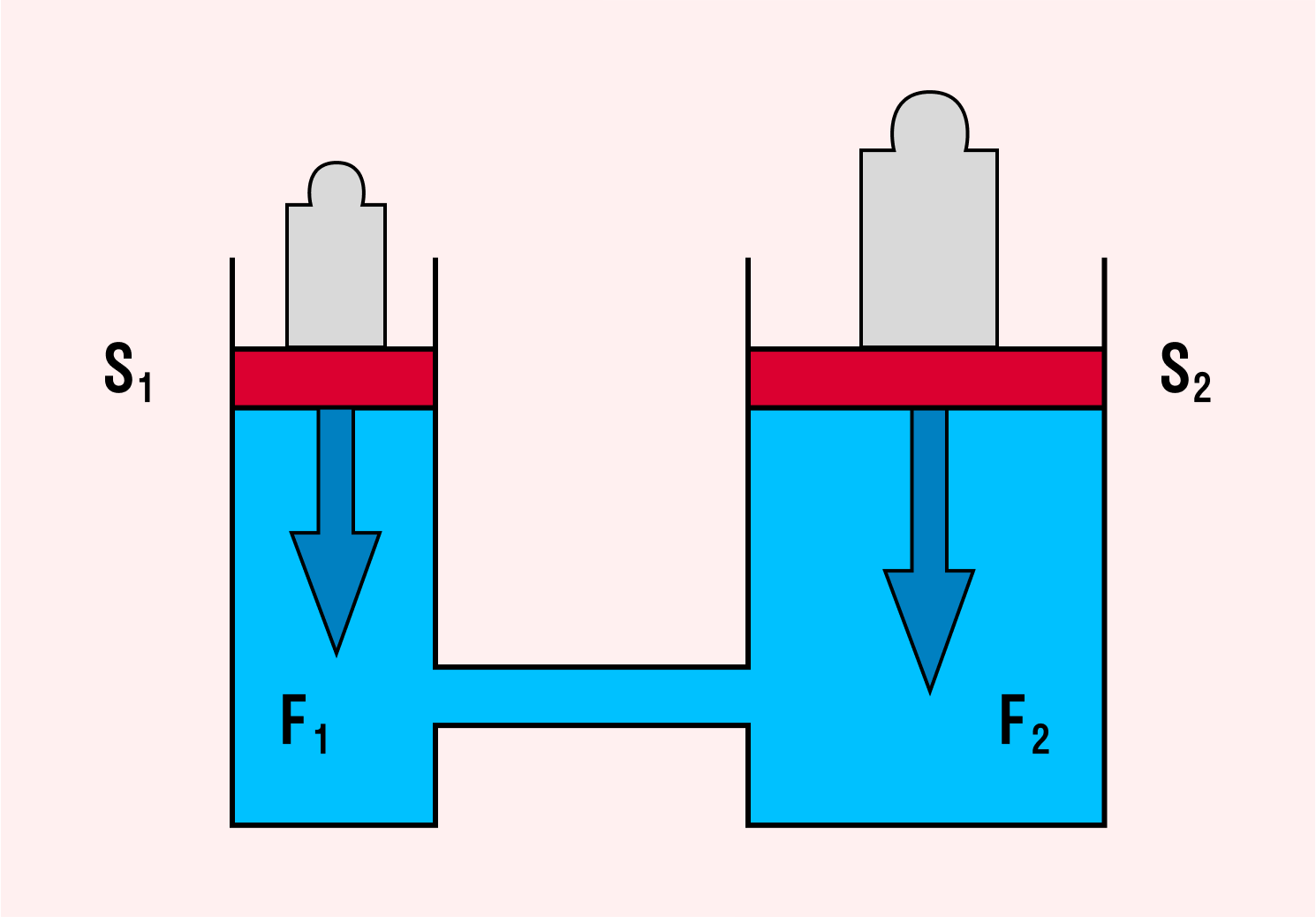
Гидравлический пресс — это механизм, созданный на основе сообщающихся сосудов разных сечений, заполненных однородной жидкостью. Такое устройство позволяет получить выигрыш в силе для оказания статического давления на детали (сжатия, зажимания и т. д.).

Если под поршнем 1 образуется давление p₁ = f₁/s₁, а под поршнем 2 будет давление p₂ = f₂/s₂, то, согласно закону Паскаля, p₁ = p₂

Силы, действующие на поршни гидравлического пресса F₁ и F₂, прямо пропорциональны площадям этих поршней S₁ и S₂.

Другими словами, сила поршня 1 больше силы поршня 2 во столько раз, во сколько его площадь больше площади поршня 2. Это позволяет уравновесить в гидравлической машине с помощью малой силы многократно бóльшую силу.

Закон Архимеда

Сила выталкивания тела, погруженного в жидкость или газ, равна весу данной жидкости или газа в таком же объеме, как у этого тела.

Формула архимедовой силы:

Закон Архимеда помогает рассчитать, как поведет себя тело при погружении в среды разной плотности. Верны следующие утверждения:

если плотность тела выше плотности среды, оно уйдет на дно;

если плотность тела ниже, оно всплывет на поверхность.

Другими словами, тело поднимется на поверхность, если архимедова сила больше силы тяжести.

Работа, энергия, мощность

Механическая работа — это скалярная величина, которая равна произведению перемещения тела на модуль силы, под действием которой было выполнено перемещение. Подразумевается, что перемещение произошло в том же направлении, в котором действует сила.

Формула работы в курсе физики за 7 класс:

A = F × S, где F — действующая сила, S — пройденный телом путь.

Единица измерения работы в СИ: джоуль (Дж).

Такое понятие, как мощность, описывает скорость выполнения механической работы. Оно говорит о том, какая работа была совершена в единицу времени.

Мощность — это скалярная величина, равная отношению работы к временному промежутку, потребовавшемуся для ее выполнения.

Формула мощности:

N = A / t, где A — работа, t — время ее совершения.

Также мощность можно вычислить, зная силу, воздействующую на тело, и среднюю скорость перемещения этого тела.

N = F × v, где F — сила, v — средняя скорость тела.

Единица измерения мощности в СИ: ватт (Вт).

Тело может совершить какую-либо работу, если оно обладает энергией — кинетической и/или потенциальной.

Кинетической называют энергию движения тела. Она говорит о том, какую работу нужно совершить, чтобы придать телу определенную скорость.

Потенциальной называется энергия взаимодействия тела с другими телами или взаимодействия между частями одного целого. Потенциальная энергия тела, поднятого над Землей, характеризует, какую работу должна совершить сила тяжести, чтобы опустить это тело снова на нулевой уровень.

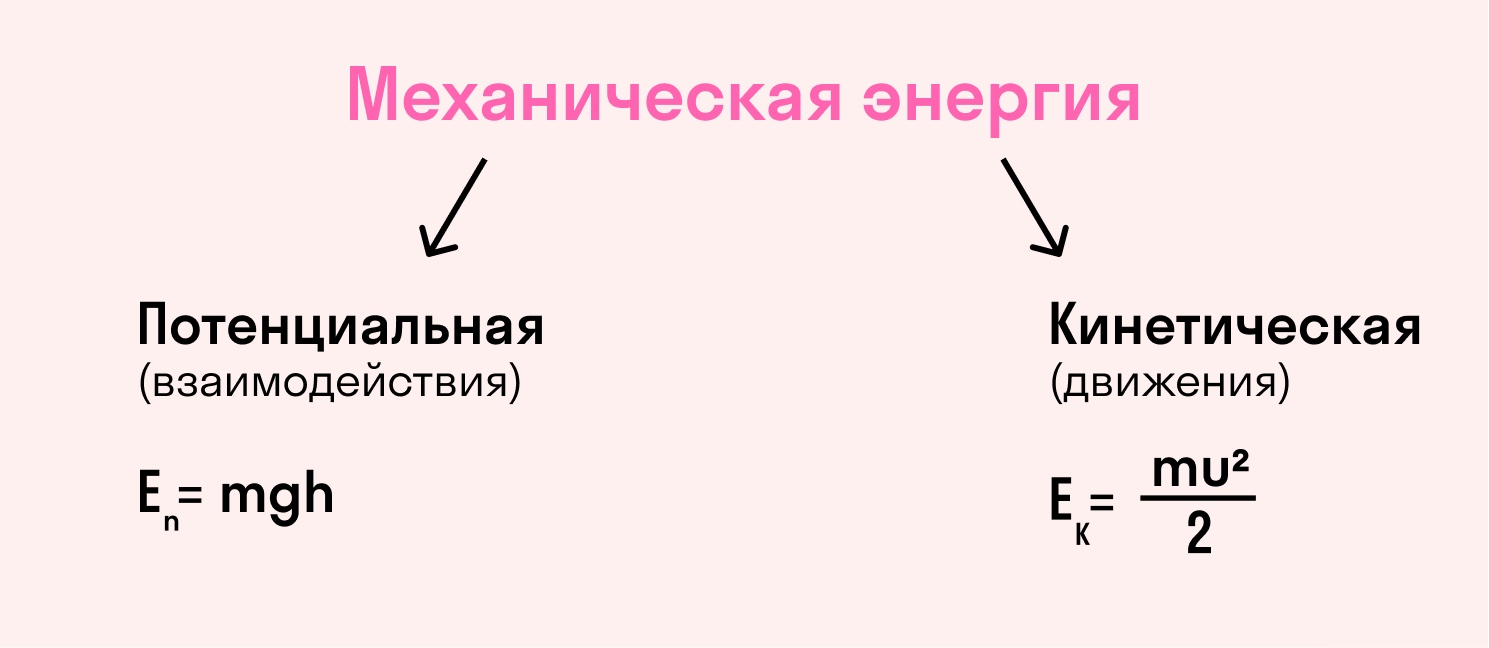
Таблица с формулами по физике за 7 класс для вычисления кинетической и потенциальной энергии:

Кинетическая энергия

Пропорциональна массе тела и квадрату его скорости.

Потенциальная энергия

Равна произведению массы тела, поднятого над Землей, на ускорение свободного падения и высоту поднимания.

Полная механическая энергия

Складывается из кинетической и потенциальной энергии.

Сохранение и превращение энергии

Если механическая энергия не переходит в другие формы, то сумма потенциальной энергии и кинетической представляет собой константу.

Для того, чтобы понять, какая часть совершенной работы была полезной, вычисляют коэффициент полезного действия или КПД. С его помощью определяется эффективность различных механизмов, инструментов и т. д.

Коэффициент полезного действия (КПД) отражает полезную часть выполненной работы. Также его можно выразить через отношение полезно использованной энергии к общему количеству полученной энергии.

Формула для расчета КПД:

где А_п— полезная работа, А_з— затраченная работа.

КПД выражается в процентах и составляет всегда меньше 100%, поскольку часть энергии затрачивается на трение, повышение температуры воздуха и окружающих тел, преодоление силы тяжести и т. д.

Источник