что такое процентиль в статистике

Что такое процентиль?

Что такое процентиль?

Термин ″процентиль″ (percentile) часто встречается в зарубежной литературе про инвестиции и вообще в статистических исследованиях – одно из таких исследований я упоминал в этой статье. Другими вариантами русских названий являются ″персентиль″ и ″перцентиль″. Думаю, что небольшая известность термина в России не вполне заслужена, поскольку нередко именно в процентилях удобно выразить полученные результаты.

Процентиль это определенная часть выборки данных

Возьмем простой пример. Группа студентов из 200 человек пишет тест, состоящий из 100 вопросов. Проходной порог, когда тест считается сданным, составляет 2/3 правильных ответов, т.е. не менее 66. Что получается с точки зрения отдельного студента?

Допустим, Иван правильно ответил на 70 вопросов. Задачу он выполнил — тест засчитан. Результат каждого участника теста также сравнивается с числом 66: если правильных ответов больше, тест сдан. В результате формируется список сдавших и не сдавших: каждый студент проходил через это. Пока ничего нового.

Но задачу можно поставить и по-другому: нужно сравнить результаты студентов не с проходным баллом в 66 пунктов, а между собой. Зачем это нужно? В данном случае, например, для объективной оценки сложность теста, что достигается группировкой результатов.

Вернемся к Ивану, который получил 70 правильных ответов. Много это или мало по сравнению с остальными? Это и покажет процентиль.

Процентили делят всю выборку на определенные части. Например, пятый процентиль охватывает 5% объема выборки. Предположим, показатель Ивана равен пятому процентилю. Это означает, что Иван написал тест лучше, чем 5% студентов (10 человек из 200 получили от нуля до 70 баллов). Не густо, поскольку в этом случае остальные 190 человек набрали больше, чем 70. Значит, тест был очень легкий и порог в 66 баллов можно и повысить.

Но в том же самом тесте может быть и обратная ситуация: результат Ивана равен 90-ому процентилю. Это значит, что Иван написал тест лучше, чем 90% студентов. Или по другому: только 10% (20 человек) набрали более 70 правильных ответов. Следовательно, тест был весьма трудным. Преимущество метода еще и в том, что разбивкой на процентили можно сравнивать тесты с разным числом участников.

Функция Гаусса

Чем более высок процентиль, тем больше данных он включает

Расчет процентиля в Excel

Процентиль несложно вычислить по формуле:

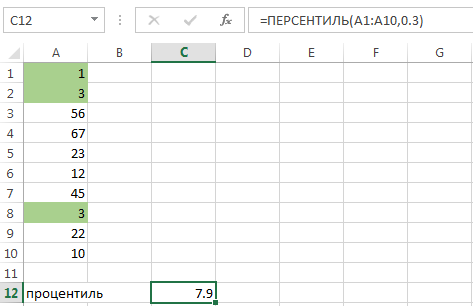
но проще обрабатывать массив данных одноименной функцией Excel. Для примера возьмем произвольную выборку полученных баллов и рассчитаем в ней процентили:

Функция PERCENTILE (ПЕРСЕНТИЛЬ) включает в себя ввод диапазона ячеек данных (А1:А10) и значения процентиля К, деленного на 100%. Т.е. в данном случае ввод 0.3 означает нахождение тридцатого процентиля. Смысл расчета: к 30-му процентилю будут относиться все результаты, меньше или равные 7.9.

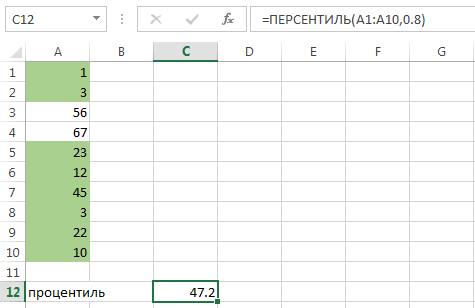
Если мы хотим узнать процентиль участника, получившего 10 баллов, то это несложно сделать, варьируя значение К до тех пор, пока значение в ячейке С12 не станет близким 10. Получится примерно 34-ый процентиль. При увеличении процентиля в выборку попадает больше табличных значений:

Итого, в 80-ый процентиль попадает уже 8 табличных значений из 10, которые меньше или равны 47.2. При этом подчеркнуть результат можно диапазоном процентилей — например, между восьмидесятым и сотым. В этом случае значения будут лежать между 47.2 и 67 (максимальным числом выборки).

Источник

Процентиль

Кванти́ль (или проценти́ль) в математической статистике — число, такое что заданная случайная величина не превышает его лишь с фиксированной вероятностью.

Содержание

Определение

.

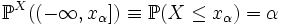
Квантили нормального распределения

Вероятность,%	99,99	99,90	99,00	97,72	97,50	95,00	90,00	84,13	50,00
Квантиль	3,715	3,090	2,326	2,000	1,960	1,645	1,282	1,000	0,000

Замечания

где F_X — функция распределения .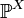

Медиана и квантили

Примеры

Полезное

Смотреть что такое «Процентиль» в других словарях:

ПРОЦЕНТИЛЬ — (реrcentile) Значения, выделяющие 100 е части распределения, выстроенные в ряд по их величине. 99 й процентиль распределения дохода, например, представляет собой такой уровень дохода, когда только один процент населения имеет больший доход.… … Экономический словарь

процентиль — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN percentile … Справочник технического переводчика

Процентиль — показатель того, какой процент значений находится ниже определённого уровня. Например, значение 50 й процентили указывает, что 50% значений располагается ниже этого уровня … Энциклопедический словарь по психологии и педагогике

ПРОЦЕНТИЛЬ — Любая из 99 пронумерованных точек, которые делят упорядоченный набор значений на 100 частей, каждая из которых содержит 1/100 ю от общего значения. Это прямое значение, к сожалению, часто путается; см. центиль и партиль для обсуждения … Толковый словарь по психологии

процентиль — Процентили – это величины, делящие выборку данных на сто групп, содержащих (по возможности) равное количество наблюдений. Например, 30% данных имеют значение, меньшее 30 го процентиля. См. тж. квантиль … Словарь социологической статистики

SAT — У этого термина существуют и другие значения, см. SAT (значения). SAT Reasoning Test (а также «Scholastic Aptitude Test» и «Scholastic Assessment Test», дословно «Школьный Оценочный Тест») стандартизованный тест для приема в высшие учебные… … Википедия

квантиль — 3.32 квантиль (fractile): р квантиль (квантиль уровня р или процентиль) и соответствующее значение квантили хропределяется как: F(xp) = p, (3.1) где F функция распределения для хр. Источник … Словарь-справочник терминов нормативно-технической документации

Алкогольный синдром плода (fetal alcohol syndrome) — А. с. п. представляет собой комплекс физ. аномалий и нейроповеденческого дефицита, к рый может серьезно поражать потомство сильно пьющих матерей. Менее серьезные последствия тяжелой алкоголизации матерей обычно обозначаются как алкогольные… … Психологическая энциклопедия

Статистика в психологии (statistics in psychology) — Первое применение С. в психологии часто связывают с именем сэра Фрэнсиса Гальтона. В психологии под «статистикой» понимается применение количественных мер и методов для описания и анализа результатов психол. исслед. Психологии как науке С.… … Психологическая энциклопедия

Медиана (статистика) — В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете … Википедия

Источник

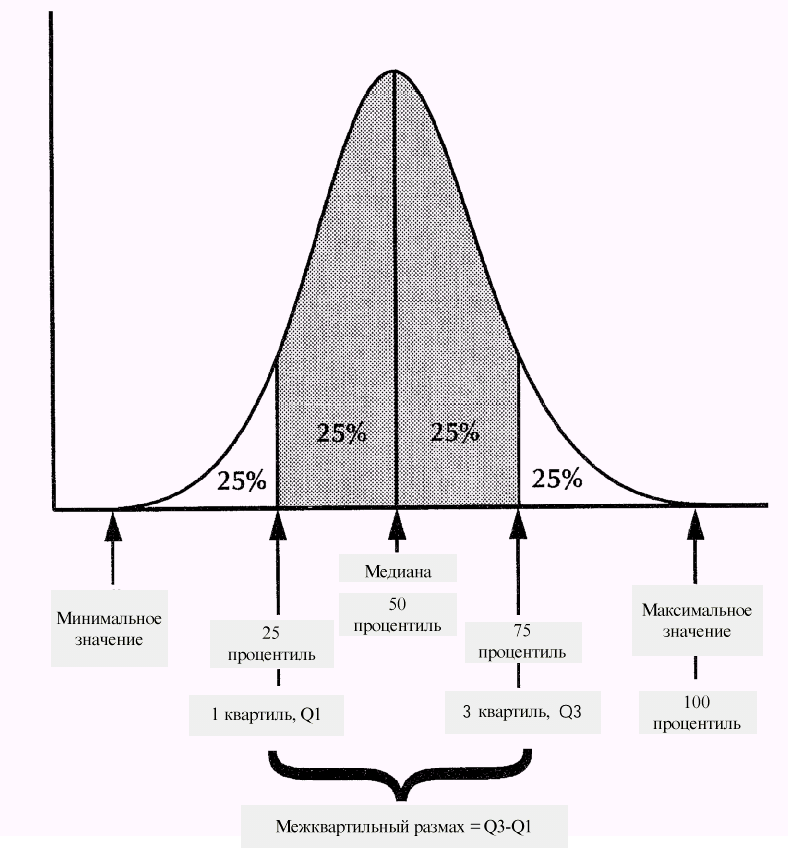
Обсудив меры центральной тенденции, рассмотрим подход к описанию положения статистических данных, который включает в себя определение пороговых значений, в пределах которых лежат указанные пропорции данных.

Мы знаем, что медиана делит распределение пополам. Мы можем определить другие разделительные линии, которые разбивают распределение на меньшие части.

Например, первый квартиль (Q₁) делит распределение так, что 25 процентов наблюдений лежат не выше него; следовательно, 1-й квартиль также является 25-м процентилем.

Второй квартиль (Q₂) представляет 50-й процентиль, а третий квартиль (Q₃) представляет 75-й процентиль, потому что 75 процентов наблюдений лежат не выше него.

Имея дело с фактическими данными, мы часто обнаруживаем, что нам нужно найти приблизительное значение процентиля. Например, если нас интересует значение 75-го процентиля, мы можем обнаружить, что ни одно наблюдение не разделяет выборку так, что ровно 75 процентов наблюдений лежат не выше этого значения.

Следующая процедура, однако, может помочь нам определить или оценить процентиль. Процедура включает в себя сначала определение положения процентиля в наборе наблюдений, а затем определение (или оценку) значения, связанного с этой позицией.

Формула для позиции процентиля в массиве из n записей, отсортированных по возрастанию:

Ly = (n + 1) y / 100 (формула 8)

В качестве примера случая, когда L_y не является целым числом, предположим, что мы хотим определить 3-ий квартиль доходности за 2012 год (Q₃ или P₇₅) для 16 европейских фондовых рынков, представленных в Таблице 8.

В соответствии с Формулой 8 позиция третьего квартиля имеет вид L₇₅ = (16 + 1) (75/100) = 12.75 или между 12-м и 13-м позициями в Таблице 9, в которой доходность представлена в порядке возрастания.

Определив «0.75» как «12.75», мы пришли бы к выводу, что P75 находится на 75% расстояния между 15.90% и 20.72%.

Подведем итоги:

1) Когда позиция Ly представляет собой целое число, она соответствует фактическому наблюдению. Например, если бы Дания не была включена в выборку, то n + 1 было бы равно 16, а при L₇₅ = 12 третий квартиль был бы P₇₅ = X₁₂, где X_i определяется как значение наблюдения в i-й (i = L₇₅) позиции данных, отсортированных в порядке возрастания (т. е. P₇₅ = 15.90).

2) Когда L_y не является целым числом, L_y лежит между двумя ближайшими целыми числами (одно сверху и одно снизу), и мы используем линейную интерполяцию между этими двумя положениями для определения P_y. Интерполяция означает оценку неизвестного значения на основе двух известных значений, которые его окружают (лежат над и под ним); термин «линейный» относится к линейной оценке.

Возвращаясь к расчету P₇₅ для доходности капитала, мы обнаружили, что L_y = 12.75; следующее более низкое целое число равно 12, а следующее более высокое целое число равно 13.

Используя линейную интерполяцию, находим:

Как указано выше, на 12-й позиции находится доходность акций Франции, поэтому X₁₂ = 15.90%; X₁₃ = 20.72%, что соответствует доходности акций Австрии.

Таким образом, наша оценка методом линейной интерполяции составит:

Мы следуем этой схеме всякий раз, когда L_y не является целым числом: ближайшие целые числа ниже и выше L_y устанавливают позиции наблюдений, которые ограничивают P_y, а затем используются для интерполяции.

Пример, приведенный ниже иллюстрирует расчет различных квантилей для дивидендной доходности компонентов основного европейского индекса акций.

Пример расчета процентилей, квартилей и квинтилей.

Рыночная капитализация ранжируется в порядке возрастания.

Таблица 17. Рыночная капитализация EURO STOXX 50.

Рыночная
капитализация
(млрд. Euro)

Источник

Процентиль: как оцениваются результаты тестов

Как сравнить потенциал двух кандидатов из разных городов, с разными культурными ценностями и образованием? Стандартизированные выборки слишком неточны, а набор контрольных групп для каждой профессии и должности слишком дорого стоит. Гораздо проще оценить претендента по результатам других кандидатов на ту же должность. Это как раз то, для чего нужен процентиль.

Как оценивают персонал

Требования к уровню соискателей растут с каждым годом, что приводит к необходимости использования комплексных методов оценки при наборе на работу.

В международных компаниях остро стоит вопрос о стоимости одного собеседования.

Рекрутеру нужно не только отобрать подходящую анкету, но и созвониться с человеком, протестировать его, интерпретировать показатели и сравнить с другими соискателями на эту должность.
Чтобы упростить эту задачу, HR используют тесты способностей и потенциала:

Как только рекрутер получил показатели нескольких претендентов, ему приходится сравнивать их, выбирая подходящего.

Как сравнивают соискателей

Возникает вопрос – как сравнить между собой людей с разным уровнем образования, опытом, культурными ценностями. Одни и те же тесты используют для подбора менеджеров и директоров – очевидно, что нельзя интерпретировать оценку этих двух групп одинаково, устанавливая минимальное количество заданий, которые должен решить соискатель.

Ситуация усложняется, когда тесты используют для отбора людей на стажировки, кадровые конкурсы и т.д. Пример – всероссийский кадровый конкурс Лидеры России. Чтобы попасть во второй тур конкурса, придется пройти дистанционный этап, включающий тестирование потенциала (PiF) и способностей (числовые, вербальные, логические).

Пример отчета по тестам (результат с процентилями)

Классический подход здесь не работает – если устанавливать проходной балл для каждой должности, придется проводить исследования, набирать контрольные группы и выборки. Гораздо проще сравнивать показатели одного человека, основываясь на результатах других претендентов на ту же должность. Эту функцию в тестах при приеме на работу выполняет перцентиль.

Что такое процентиль

В математической статистике процентиль (или перцентиль, percentile) — это доля людей из выборки, результат которых ниже определенного показателя.

Если, 38% людей правильно ответят на 10 вопросов числового теста, показателю 10 соответствует 38-й перцентиль.

Таким образом, получит человек приглашение на собеседование или нет, зависит от того, как он пройдет испытание по сравнению с другими кандидатами на ту же должность.

Сколько набрать

Нижняя граница, при которой кандидаты не проходят на собеседование, определяется каждой компанией или разработчиком тестирования. Например, SHL рекомендует отсеивать кандидатов, если они не набирают 30-й перцентиль. Однако это справедливо для средних должностей, где не нужны развитые способности к анализу информации.

Перцентили используются не только в тестах SHL или TalentQ, но и в психологических опросниках, например, результат теста Кеттела также оценивается в процентилях.

Для должностей топ уровня, например, для директоров, начальников департаментов SHL рекомендует использовать 60-й перцентиль.

Тем не менее в большинстве российских компаний минимальный проходной балл установлен на уровне 65-го процентиля. То есть, чтобы попасть на очное собеседование, задания придется решить лучше, чем 65% кандидатов на ту же должность.

Стоит ли гнаться за 100%

Некоторые люди стремятся быть лучшими во всем, в том числе, в тестировании, пытаясь набрать 100%. Но такой подход лишен смысла.

Некоторые работодатели используют оценочные испытания чисто формально – главное, чтобы кандидат получил оценку выше проходной, а как он это сделал – неважно. Но большинство компаний относится к вопросам тестирования серьезно.

Работодатели начинают осознавать ценность тестирования и все серьезнее относятся к его результатам. Сегодня ретест уже не редкость — он проводится почти на каждом собеседовании.

Помимо дистанционного этапа, оценку подтверждают очно, на ретесте. Если на дистанционном этапе потенциальный сотрудник показал 98%, а придя в офис к работодателю, не набирает 30%, с ним прекращают диалог.

Так сколько нужно процентов?

Исследования показывают четкую связь между слабыми результатами тестов способностей и обучаемостью. Однако корреляции между высокой оценкой и его эффективностью нет. Соискатель, набравший 98% не лучше набравшего 70%.

На оценку влияет мотивация и способность выполнять рутинные задачи. Некоторым людям с потенциалом надоедают рутинные задачи. Поэтому идеальным считается оценка на 10-15% превышающая проходную.

Как пройти на собеседование

Работодатели, как правило, не сообщают о подробностях тестирования. Эта информация отвлекает кандидата, кроме того, если человек знает, сколько «баллов» ему придется набрать, он начинает сильнее волноваться, что искажает результат.

Иногда работодатели не ведут диалога с соискателем до очного собеседования, направляя ссылку на корпоративный портал с тестированием.

Но это не значит, что человек не может поинтересоваться о процедуре тестирования у рекрутера. Чаще всего рекрутеры охотно идут на диалог, давая дельные советы. Ведь рекрутер тоже заинтересован в том, чтобы «захантить» хорошего кандидата. А контакт — это показатель мотивации и целеустремленности.

Как использовать перцентиль в свою пользу

Хотя за процентилем гнаться не нужно, рекомендуется стремиться показать результат на 15-20% выше, чем проходной. В этом случае его используют в качестве дополнительного аргумента при трудоустройстве, ведь работодателю нужны сотрудники, обладающие потенциалом к развитию и навыками работы с информацией.

Независимо от исхода тестирования или процентиля, важно получить отчет соискателя – его используют при трудоустройстве в другие компании, ведь оценка действительна в течение 1-1,5 лет.

Как тренироваться

При использовании тренировочных упражнений, в Личном кабинете пользователю доступно сравнение показателей с другими пользователями.

Хотя это сравнение грубее, поскольку не учитывает должности или компании, оно с достаточной точностью предсказывает результаты реальной оценки. Нормативная выборка составляет десятки тысяч пользователей разных возрастов и профессий, которые когда-либо решали эти задачи.

В тренировочных задачах рекомендуется ориентироваться на 80-й перцентиль. Это гарантирует, что у работодателя результат окажется не ниже.

Для улучшения результата недостаточно следить за перцентилем, рекомендуется анализировать ошибки и следить за развитием навыка. Получив определенный балл в тренировочном тесте, выполняют работу над ошибками, смотрят правильное решение и пытаются понять, из-за чего возникла ошибка.

К этому вопросу возвращаются спустя несколько дней. Так повышается не только процентиль, но и навык решения задач.

Заключение

Процентиль – это не только оценка результатов теста, это еще и показатель готовности к собеседованию и эффективности тренировочного процесса. А если правильно тренироваться, отрабатывать ошибки и следить за своим прогрессом, никаких сложностей с тестами на собеседовании или на ретесте у кандидата не возникнет.

Источник

Методы ближайшего ранга (исключающие / включающие)

ПК: указан процентиль	0,10	0,25	0,50	0,75	0,90
N: количество баллов	10	10	10	10	10
ИЛИ: порядковый номер = ПК × N	1	2,5	5	7,5	9
Ранг:> ИЛИ / ≥ИЛИ	2/1	3/3	6/5	8/8	10/9
Оценка в рейтинге (отл. / Вкл.)	2/1	3/3	4/3	5/5	7/5

На рисунке показано 10-балльное распределение, показаны процентильные баллы, полученные в результате использования этих различных алгоритмов, и он служит введением в приведенные ниже примеры. Самыми простыми являются методы ближайшего ранга, которые возвращают оценку из распределения, хотя по сравнению с методами интерполяции результаты могут быть немного грубыми. В таблице методов ближайшего ранга показаны этапы вычислений для исключающих и инклюзивных методов.

Методы интерполяции, как следует из названия, могут возвращать оценку, которая находится между оценками в распределении. Алгоритмы, используемые статистическими программами, обычно используют методы интерполяции, например, функции percentile.exl и percentile.inc в Microsoft Excel. В таблице Interpolated Methods показаны этапы вычислений.

СОДЕРЖАНИЕ

Приложения

85-й процентиль скорости движения на дороге часто используется в качестве ориентира при установлении ограничений скорости и оценке того, является ли такой предел слишком высоким или низким.

В финансах стоимость, подверженная риску, является стандартной мерой для оценки (в зависимости от модели) величины, при которой не ожидается снижения стоимости портфеля в течение заданного периода времени и с учетом значения достоверности.

Нормальное распределение и процентили

Определения

Стандартного определения процентиля не существует, однако все определения дают аналогичные результаты, когда количество наблюдений очень велико, а распределение вероятностей является непрерывным. В пределе, когда размер выборки приближается к бесконечности, 100 p- й процентиль (0 Условное обозначение

Метод ближайшего ранга

Одно определение процентиля, часто приводимое в текстах, заключается в том, что P-й процентиль списка из N упорядоченных значений (отсортированных от наименьшего к наибольшему) является наименьшим значением в списке, так что строгое не более P процентов данных меньше значения и по крайней мере P процентов данных меньше или равно этому значению. Для этого сначала вычисляется порядковый ранг, а затем берется значение из упорядоченного списка, которое соответствует этому рангу. Порядковое ранга п вычисляется по следующей формуле ( 0 п ≤ 100 ) <\ displaystyle (0

Обратите внимание на следующее:

Рабочие примеры метода ближайшего ранга

Рассмотрим упорядоченный список <15, 20, 35, 40, 50>, который содержит 5 значений данных. Каковы 5-й, 30-й, 40-й, 50-й и 100-й процентили этого списка с использованием метода ближайшего ранга?

Таким образом, 5-й, 30-й, 40-й, 50-й и 100-й процентили упорядоченного списка <15, 20, 35, 40, 50>с использованием метода ближайшего ранга равны <15, 20, 20, 35, 50>.

Рассмотрим упорядоченную совокупность из 10 значений данных <3, 6, 7, 8, 8, 10, 13, 15, 16, 20>. Каковы 25-й, 50-й, 75-й и 100-й процентили этого списка с использованием метода ближайшего ранга?

Таким образом, 25-й, 50-й, 75-й и 100-й процентили упорядоченного списка <3, 6, 7, 8, 8, 10, 13, 15, 16, 20>с использованием метода ближайшего ранга равны <7, 8, 15, 20 >.

Рассмотрим упорядоченную совокупность из 11 значений данных <3, 6, 7, 8, 8, 9, 10, 13, 15, 16, 20>. Каковы 25-й, 50-й, 75-й и 100-й процентили этого списка с использованием метода ближайшего ранга?

Метод линейной интерполяции между ближайшими рангами

Альтернативой округлению, используемым во многих приложениях, является использование линейной интерполяции между соседними рангами.

Общность вариантов этого метода

Все следующие варианты имеют следующее общее. Учитывая статистику заказа

и наша измененная функция теперь имеет только одну степень свободы, которая выглядит так:

Первый вариант, C = 1/2

(Источники: функция Matlab «prctile»)

Обратное соотношение ограничено более узкой областью:

Рабочий пример первого варианта

Рассмотрим упорядоченный список <15, 20, 35, 40, 50>, который содержит пять значений данных. Каковы 5-й, 30-й, 40-й и 95-й процентили этого списка с использованием метода линейной интерполяции между ближайшими рангами? Сначала мы вычисляем процентный рейтинг для каждого значения списка.

Затем мы берем эти процентные ранги и вычисляем значения процентилей следующим образом:

Учитывая эти значения, мы можем вычислить v следующим образом:

Таким образом, 5-й, 30-й, 40-й и 95-й процентили упорядоченного списка <15, 20, 35, 40, 50>с использованием метода линейной интерполяции между ближайшими рангами равны

Второй вариант, C = 1

(Источник: некоторые программные пакеты, включая NumPy и Microsoft Excel (до версии 2013 включительно с помощью функции PERCENTILE.INC). Отмечено NIST в качестве альтернативы )

Рабочие примеры второго варианта

Пример 1

Рассмотрим упорядоченный список <15, 20, 35, 40, 50>, который содержит пять значений данных. Каков 40-й процентиль этого списка при использовании этого вариантного метода?

Сначала мы вычисляем ранг 40-го процентиля:

Пример 2

Рассмотрим упорядоченный список <1,2,3,4>, который содержит четыре значения данных. Каков 75-й процентиль этого списка при использовании метода Microsoft Excel?

Сначала мы вычисляем ранг 75-го процентиля следующим образом:

Итак, x = 3,25, что дает нам целую часть 3 и дробную часть 0,25. Итак, значение 75-го процентиля равно

Третий вариант, C = 0

Обратное ограничено более узкой областью:

Рабочий пример третьего варианта

Рассмотрим упорядоченный список <15, 20, 35, 40, 50>, который содержит пять значений данных. Каков 40-й процентиль этого списка с использованием метода NIST?

Сначала мы вычисляем ранг 40-го процентиля следующим образом:

Таким образом, значение 40-го процентиля упорядоченного списка <15, 20, 35, 40, 50>при использовании этого варианта метода равно 26.

Метод взвешенных процентилей

сумма весов. Затем приведенные выше формулы обобщаются, взяв

Источник