что такое пролет балки

Как определить расчетный пролет балки (плиты, перемычки)

При расчете любого изгибаемого элемента, будь то плита, балка или перемычка, прежде всего, следует определить расчетный пролет. При переводе объемных конструкций в плоскую расчетную схему очень важно задаться правильными размерами элементов. Ведь в расчетной схеме все просто: балка – это стержень, а опора – точка. На самом же деле опора имеет свой размер – глубину опирания, и балка не зависает на краях стены (от точки до точки), часть ее работает в пролете, но часть – «отдыхает» на опорах.

Создавая расчетную схему, мы сталкиваемся с двумя величинами: реальной длиной балки и расстоянием в свету между опорами. Какую из этих величин следует принять за расчетную? Если брать полную длину балки, это будет неверно, т.к. все-таки та ее часть, которая лежит на опоре, не подвержена таким напряжениям, как в пролете. Но брать за расчетную длину расстояние между опорами можно только в отдельных случаях, ниже мы рассмотрим, что да как.

Далеко не всегда расчетная длина балки совпадает с пролетом в свету между опорами.

Есть два варианта размера расчетного пролета.

1) Если опирание жесткое, т.е. балка защемлена на опоре (либо является частью монолитной конструкции), то расчетный пролет L₀ равен расстоянию в свету между опорами.

2) Если же опирание шарнирное, то расчетный пролет всегда больше этого расстояния.

Рассмотрим глубже определение расчетного пролета при шарнирном опирании элемента. Во-первых, следует четко определиться с требованиями глубины опирания шарнирных элементов (поможет статья «В чем разница между шарнирным опиранием и жестким защемлением»). Если вы делаете расчет шарнирно опираемой железобетонной балки (плиты и т.п.), глубина ее опирания должна быть не более высоты сечения – иначе, это будет уже защемление или переходное состояние между шарниром и защемлением, а там и расчет другой, и длина расчетного пролета – согласно пункту 1. Т.е. если вы плиту толщиной 200 мм опираете на 450 мм с каждой стороны, то пользоваться нижеприведенным расчетом не следует.

Для ленивых во многих учебниках есть правило: L₀ = 1.05L, т.е. берем расстояние между опорами в свету и умножаем на 1,05.

Но сейчас мы постараемся понять, в чем же суть увеличения расчетного пролета, и как поточнее его определить.

При расчете балки мы привыкли получать реакции на опоре в виде сосредоточенных сил.

Но если рассмотреть точнее, нагрузка от балки на опору передается в виде распределенной нагрузки, причем даже не равномерно распределенной: максимальная ее величина расположена у края опоры, а к концу балки она сходит на нет.

По общепринятым правилам перевода распределенной нагрузки в сосредоточенную, положение сосредоточенной нагрузки будет в центре тяжести треугольника, т.е. на расстоянии 1/3 от края опоры. В этом же месте будет расположена искомая реакция. А расстояние между этими реакциями будет равно расчетному пролету.

Таким образом, если глубина опирания балки с одной стороны равна А, а с другой стороны В, то расчетный пролет мы найдем по формуле:

Если же глубина опирания с двух сторон одинаковая и равна А, то

Такое увеличение расчетного пролета по отношению к реальному (в районе 5%) дает определенный запас прочности и приближает нас к реальному положению вещей – ведь длина балки может быть разной, а глубина опирания обычно одинаковая. И пять процентов при трехметровом пролете значительно отличается от пяти процентов при восьмиметровом.

Источник

Высота балки в зависимости от пролета

1. Определяем высоту сечения балки.

Минимальная высота должна быть не менее 1/15 пролета. Пример: для пролета 6 м, минимальная высота равна:

2. Определяем ширину балки.

Ширина балки от 100 мм. Отношение h/b=2. 4. Пример:

h=400 мм, b=400/2=200мм

Если балка заливается с колонной, как правило ширина принимается как у колонны.

3. Определение расчетной схемы.

Условия, при которых опору можно считать жесткой защемленной а не шарнирной:

В остальных случаях — шарнирная опора.

4. Сбор нагрузок

300 кг/м2
трибуны с сидениями

400 кг/м2
трибуны без сидений

500 кг/м2
Вес пола со стяжкой

5. Расчет балки

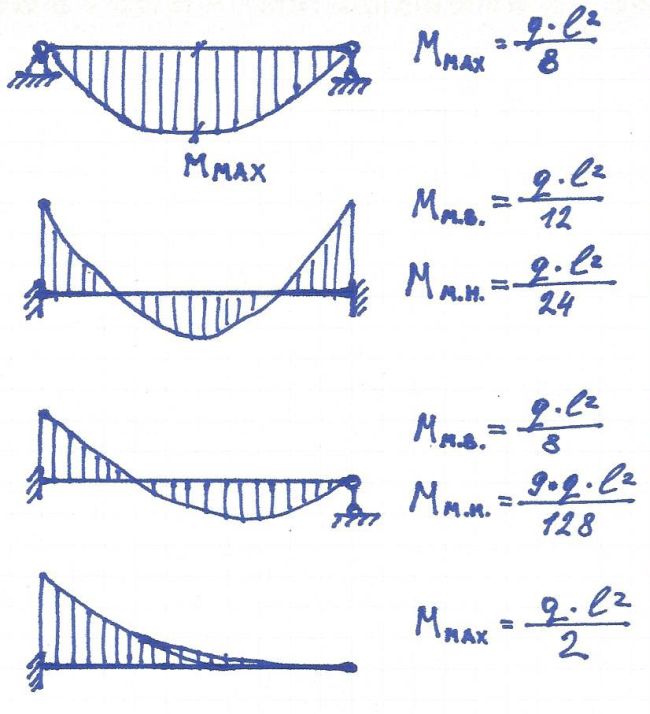
Далее, имея размеры сечения, пролет и нагрузку, можно выполнить расчет. Есть два пути: выполнить расчет программой для компьютера или считать вручную. Для ручного расчета нужно определить изгибающий момент усилия в балке и подобрать необходимое количество арматуры. Формула для определения максимального момента сил зависит от рассчетной схемы балки (см. п.3).

Момент сил в балках от распределенной нагрузки

Подбор количества арматуры производится по формулам и таблицам.

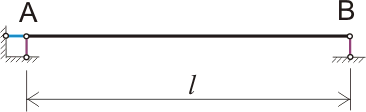
Генеральными размерами балки являются ее расчетный пролет и высота сечения. Расчетный пролет балки l представляет собой расстояние между центрами опорных частей; таким образом, действительная длина балки l_д всегда несколько больше расчетного пролета.

Расстояние l называется расстоянием в свету; оно обычно определяется условиями эксплуатации вооружения и обосновывается экономическими соображениями.

Генеральные размеры балок

Значения величины — 1/n для балок, имеющих различное назначение, устанавливаются нормами (смотрите Коэффициенты условий работы m).

Отношение прогиба балки к пролету находится в прямой зависимости от отношения высоты сечения к пролету. Обозначив постоянную равномерно распределенную нагрузку через р, а временную через q, найдем для разрезной балки наибольший изгибающий момент

где n_p и n_q — соответствующие коэффициенты перегрузки.

Как указывалось в разделе Основы проектирования, при определении прогибов принимается нормативная нагрузка (без учета коэффициентов перегрузки).

Тогда с учетом формулы найдем прогиб от нормативной нагрузки, выраженный через расчетные напряжения в балке:

Из формулы получим зависимость относительного прогиба от высоты балки

Отсюда можно определить минимальную высоту балки

Учитывая необходимость полного использования в балке расчетного сопротивления материала (σ = R) и принимая во внимание, что R/E = 2100/(2,1*10 6 ) = 1/1000, а также полагая n_p = n_q, приведем формулу к виду

Отношения минимальной высоты сечения балки к пролету в зависимости от прогиба (для балок из стали марки Ст. 3)

При высоте балки меньше указанной в таблице, нормативный относительный прогиб балки может быть также получен, но уже при пониженных напряжениях, т. е. с перерасходом металла.

Минимально необходимая высота балки не всегда является наивыгоднейшей по расходу стали. Вопрос о наивыгоднейшей высоте балки разобран отдельно (смотрите Составные балки).

«Проектирование стальных конструкций»,
К.К.Муханов

Плоский настил из металлического листа располагают и приваривают к полкам балок. Толщина настила назначается по расчету, чаще всего в зависимости от принятого допустимого прогиба, так как полное использование напряжений в листе при заданном прогибе не всегда возможно. Поэтому расчет листового настила ведется по нормативным нагрузкам. Особенность листового настила заключается в том, что по характеру своей…

При проектировании балочных конструкций, как правило, необходимо в зависимости от назначения балок составить схему их расположения, наметить генеральные размеры и определить приходящуюся на балки нагрузку. В случае необходимости перекрыть некоторую площадь поддерживающие перекрытие балки располагают обычно в двух направлениях. Такая конструкция, состоящая иногда из целой системы пересекающихся балок, называется балочной клеткой. На балочную клетку может…

Для того, чтобы соорудить надежное деревянное перекрытие, необходимо правильно подобрать размеры балок, а для этого необходимо сделать их расчет. Деревянные балки перекрытия имеют следующие основные размеры: длину и сечение. Их длина определяется шириной пролета, который требуется перекрыть, а сечение зависит как от нагрузки, которая будет на них действовать, от длины пролета и шага установки, то есть расстояния между ними. В данной статье мы рассмотрим, как самостоятельно сделать такой расчет и правильно подобрать размеры балок.

Содержание статьи:

Расчет балок деревянного перекрытия

Для того, чтобы определить какое количество деревянных балок и каких размеров потребуется для устройства перекрытия необходимо:

Теперь рассмотрим, как это можно сделать.

Длина деревянных балок перекрытия

Необходимая длина балок перекрытия определяется размерами того пролета, который они будут перекрывать и запасом необходимым для заделывания их в стены. Длину пролета несложно замерить с помощью рулетки, а глубина заделывания в стены, во многом, зависит от их материала.

В домах со стенами из кирпича или блоков балки обычно заделываются в «гнезда» на глубину не менее 100 мм (доска) или 150 мм (брус). В деревянных домах их, как правило, укладываютс в специальные зарубки на глубину не меньше чем 70 мм. При использовании специального металлического крепления (хомутов, уголков, кронштейнов) длина балок будет равна пролету — расстоянию между противоположными стенами, на которых они крепятся. Иногда, при монтаже стропильных ног крыши непосредственно на деревянные балки, их выпускают наружу, за пределы стен на 30-50 см, формируя, таким образом, свес крыши.

Оптимальный пролет, которые могут перекрывать деревянные балки 2,5-4 м. Максимальная длина балки из обрезной доски или бруса, то есть пролет, который она может перекрывать — 6 м. При большей длине пролета (6-12 м) необходимо использовать современные деревянные балки из клееного бруса или двутавровые, а также можно опирать их на промежуточные опоры (стены, колонны). Кроме этого для перекрытия пролетов, длиной более 6 м, вместо балок можно использовать деревянные фермы.

Определение нагрузки, действующей на перекрытие

Нагрузка, действующая на перекрытие по деревянным балкам состоит из нагрузки от собственного веса элементов перекрытия (балок, межбалочного заполнения, зашивки) и постоянной или временной эксплуатационной нагрузки (мебели, различных бытовых устройств, материалов, вес людей). Она, как правило, зависит от вида перекрытия и условий его эксплуатации. Точный расчет таких нагрузок довольно громоздкий и выполняется специалистами при проектировании перекрытия, но при желании выполнить его самостоятельно, можно использовать упрощенный его вариант, приведенный ниже.

Для чердачного деревянного перекрытия, которое не используется для складирования вещей или материалов, с легкими утеплителем (минеральная вата или др.) и подшивкой постоянная нагрузка (от собственного веса — Рсобств.) обычно принимается в пределах 50 кг/м2.

Эксплуатационная нагрузка (Рэкспл.)для такого перекрытия (согласно СНиП 2.01.07-85) составит:

Общая расчетная нагрузка, которая будет действовать на данное чердачное перекрытие составит:

В случае, если в конструкции чердачного помещения будет использоваться более тяжелый утеплитель, материал для межбалочного заполнения или подшивка, а также если предполагается его использовать для хранения вещей или материалов, то есть оно будет интенсивно эксплуатироваться, то нормативное значение нагрузки следует увеличить до 150 кг/м2. В этом случае, общая нагрузка на перекрытие составит:

Сечение и шаг балок деревянного перекрытия

Зная необходимую длину балок деревянного перекрытия (L) и определив общую расчетную нагрузку можно определить необходимое их сечение (или диаметр) и шаг укладки, которые связаны между собой. Считается, что лучшим является прямоугольное сечение балки деревянного перекрытия, с соотношением высоты (h) и ширины (s) как 1,4:1. Ширина балок, при этом, может быть в пределах 40-200 мм, а высота 100-300 мм. Высоту балок часто выбирают такой, чтобы она соответствовала необходимой толщине утеплителя. При использовании в качестве балок бревен их диаметр может быть в пределах 11-30 см.

Сделать расчет или проверку уже выбранных размеров деревянных балок перекрытия можно по справочным таблицам (некоторые приведены ниже) или используя онлайн калькулятор «расчет деревянных балок перекрытия», который легко найти в интернете, «забив» соответствующий запрос в поисковике. При этом необходимо учесть, что относительный их прогиб для чердачных перекрытий не должен быть более 1/250, а для междуэтажных – 1/350.

Таблица 1

Рекомендуемое сечение балок из бруса (s x h), в зависимости от шага их укладки и перекрываемого пролета, при общей расчетной нагрузке 350-400 кг/м 2 (междуэтажные перекрытия), мм:

Шаг,м Пролет,м

Источник

Однопролетная или многопролетная (неразрезная) балка (плита). Что выбрать?

В данной статье я буду говорить о балках. Но вся информация в ней точно так же касается и плит перекрытия, которые также бывают однопролетными и многопролетными (неразрезными).

Итак, есть балка, у которой несколько пролетов (например, на четыре колонны в ряд нужно опереть балку под перекрытие). Какую расчетную схему лучше выбрать? На чем остановиться: на обыкновенных однопролетных балках от колонны до колонны или же выбрать многопролетную – не зря же она так называется, а у нас как раз много пролетов и нужно перекрыть.

Для того, чтобы всегда делать правильный выбор, не обязательно каждый раз проводить расчет обоих балок и делать технико-экономическое сравнение. Нужно понять их особенности.

Однопролетная балка – это самый простой вариант. Она экономична в изготовлении, работает у нее только нижняя арматура (верхняя устанавливается конструктивно), рассчитать ее тоже проще простого. В чем же ее недостатки? При увеличении размеров пролета (расстояния между опорами) однопролетная балка сдает позиции. Приходится сильно увеличивать сечение, вырастает арматура, а если пролет слишком уж большой, балка просто не проходит по расчету (обычно критическим становится расчет по второму предельному состоянию – либо прогиб больше нормы, либо трещины больше допустимого).

Многопролетная (неразрезная) балка – это вариант, который используется, если однопролетной балки не достаточно для того, чтобы перекрыть слишком большие пролеты или чтобы выдержать значительную нагрузку. Многопролетная балка – это и двухпролетная, и трехпролетная, ну и так далее. Много – значит больше одного.

В чем же многопролетная балка выигрывает по сравнению с однопролетной? Количество пролетов здесь играет не очень большую роль (но об этом мы еще поговорим), а вот основное влияние в том, что балка неразрезная. А значит, она не прерывается над колоннами. Главное – не прерывается ее армирование. Правильно законструированная неразрезная балка может выдержать намного большую нагрузку и перекрыть намного больший пролет, чем однопролетная.

Рассмотрим, в чем разница в работе этих двух конструкций: однопролетной и многопролетной (неразрезной) балки. На рисунке ниже утрированно показаны деформации балок, опирающихся на колонны.

На верхней схеме каждый пролет перекрывает однопролетная балка. Опирание балок шарнирное (почему именно шарнирное, можно почитать здесь). При такой схеме балки спокойно изгибаются под весом нагрузки. Нижняя зона у них растянута (показано синим), именно у растянутой зоны устанавливается рабочая арматура, которая берет на себя все растягивающие усилия (бетон на растяжение практически не работает, сразу трещит). На опорах балки спокойно поворачиваются, этот поворот создает дополнительный прогиб плит.

На нижней схеме все три пролета перекрывает неразрезная балка. Ее работа сложнее, чем у однопролетной: под весом нагрузки в пролете балка прогибается вниз, но на опорах она выгибается в обратную сторону. И это чередование изгибов, чередование растянутых зон (синяя внизу, красная вверху) играет нам на руку. Так как у плиты не могут быть растянуты сразу две стороны, растяжение верхней зоны над опорами (красное) уменьшает растяжение нижней зоны в пролете (синее).

Если сравнить длину растянутой зоны на схеме с однопролетными балками и на схеме с неразрезной балкой, у однопролетных длина растянутой зоны балки (синей) в каждом пролете больше (при одинаковых исходных условиях – величине пролетов, нагрузках, сечении балок). А раз длина растянутой зоны больше, то и изгибающий момент будет больше, и армирование нижней зоны в пролете больше, и прогиб больше, и трещины раскроются шире – так как все эти величины взаимосвязаны.

Получается, что за счет прогиба балки над опорой в обратную сторону, мы получаем существенное сокращение всех перечисленных выше составляющих. А значит, мы создаем более выносливую конструкцию, способную легче выдержать как больший пролет, так и большую нагрузку.

В чем тогда подвох? Ведь не бывает так, чтобы где-то уменьшилось и при этом нигде не увеличилось. В случае с неразрезной балкой, в виде компенсации мы получаем растяжение в верхней зоне балки над опорой. А это значит, что в этой зоне появляется рабочая арматура (часто она бывает даже больше пролетной). Это значит, что в этой зоне появляется риск возникновения трещин (нужно выполнять проверочный расчет по второй группе предельных состояний). В общем, даром изменение расчетной схемы балке не дается.

Почему в случае с небольшим расстоянием между опорами и небольших нагрузках на балку применять неразрезные балки не стоит? Просто потому, что это не экономично – вы будете вынуждены заложить в балку не только нижнюю рабочую арматуру на всю длину балки, но и дополнительно еще верхнюю рабочую (а рабочая всегда больше конструктивной). В сумме будет перерасход арматуры по сравнению с однопролетной рабочей схемой.

Если вы хотите узнать, что бывает с недоармированной неразрезной балкой, можете ознакомиться с этой статьей.

Источник

РАСЧЕТНЫЙ ПРОЛЕТ

расстояние между центрами опирания балки, арки или фермы. В балочных фермах мостов, имеющих специальные опорные части, Р. п. равен расстоянию между центрами опорных частей. В арках величина Р. п. определяется расстоянием между центрами пят арки. В балках (деревянных, металл. и железобетонных) в случаях, когда не предусмотрено устройство специальных опорных частей, Р. п. равен отверстию в свету, увеличенному на длину опирания одного конца балки. Р. п. свободно уложенных железобетонных плит принимается равным отверстию в свету между опорами, увеличенному на толщину плиты. Величина Р. п. необходима для расчета прочности и жесткости ферм.

Смотреть что такое «РАСЧЕТНЫЙ ПРОЛЕТ» в других словарях:

Пролет — – расстояние между смежными опорами, перекрываемое балкой, плитой, аркой и пр. Расчетный пролет – расстояние между осями опор. Пролет в свету – расстояние между внутренними гранями опор … Словарь строителя

Пролет — Расстояние между смежными опорами, перекрываемое балкой, плитой, аркой и пр. Расчетный пролет расстояние между осями опор. Пролет в свету расстояние между внутренними гранями опор. Источник: Словарь архитектурно строительных терминов … Строительный словарь

Пролет моста расчетный — горизонтальное расстояние между осями опорных частей, а при отсутствии их между осями опор или условными точками опирания пролетного строения. Источник: Справочник дорожных терминов … Строительный словарь

Оловозаводской мост (Новосибирск) — Файл:Bygrinsky bridge Novosibirsk.jpg Трехмерная модель местности с будущим мостом Оловозаводской (Бугринский) мост в Новосибирске третий по счету мост через Обь в Новосибирске, строительство которого началось[1] в феврале 2010 года и… … Википедия

Коломенский мост — Коломенский … Википедия

Зеленодольский железнодорожный мост — (Романовский мост, Красный мост, Свияжский мост) … Википедия

МПБ (мост из прокатных балок) — МПБ мост из прокатных балок. Конструкции мостовые из прокатных балок предназначены для возведения мостовых переходов через узкие (до 12 м) препятствия на путях движения войск и использования в качестве пролетного строения в многопролетных… … Википедия

snip-id-9431: Технические указания по устройству, укладке, содержанию и ремонту бесстыкового пути — Терминология snip id 9431: Технические указания по устройству, укладке, содержанию и ремонту бесстыкового пути: Маячная шпала Специально обустроенная шпала, используемая для контроля продольных подвижек рельсовой плети МШ Определения термина из… … Словарь-справочник терминов нормативно-технической документации

Технические указания по устройству, укладке, содержанию и ремонту бесстыкового пути — Терминология Технические указания по устройству, укладке, содержанию и ремонту бесстыкового пути: Маячная шпала Специально обустроенная шпала, используемая для контроля продольных подвижек рельсовой плети МШ Определения термина из разных… … Словарь-справочник терминов нормативно-технической документации

Источник

Расчет балки. Общие положения

А теперь рассмотрим каждый из этих этапов более подробно.

1 этап. Определение максимальных напряжений

1.1. Определение видов и количества опор

Опоры у балки могут быть разные: шарнирные и(или) жесткие.

Рисунок 219.2.

Например, у балки, показанной на рисунке 219.2 имеется две вертикальных шарнирных опоры, показанные фиолетовым цветом и одна горизонтальная шарнирная опора, показанная синим цветом.

Как правило опоры обозначаются латинскими литерами А, В, С, D и т.д.

1.2. Определение количества и длины пролетов

Балки могут иметь не только один пролет, но два, три и сколь угодно много. Количество пролетов n_п определить не сложно:

1.3. Система координат

При расчете балок используется стандартная система координат с осями х, у и z. Для упрощения расчетов балка рассматривается как стержень, нейтральная ось которого совпадает с осью координат х. При этом начало координат как правило совпадает с началом балки. Соответственно длина балки измеряется по оси х.

Геометрические размеры поперечных сечений балки, т.е. размеры относительно осей y и z, на первом этапе расчетов никакого значения не имеют. Более того именно эти параметры и нужно определить на втором этапе расчета балки на действующие нагрузки.

Таким образом на первом этапе балка рассматривается как некий стержень, размеры сечения которого пренебрежимо малы по сравнению с длиной.

1.4. Определение действующих нагрузок

Все нагрузки, действующие на балку, можно представить в виде:

1.4.1. Сосредоточенных сил

Могут обозначаться как Q, P, N и др. Измеряются в Ньютонах (Н) или килограмм-силах (кгс).

1.4.2. Нагрузок, распределенных по некоторой части длины или по всей длине балки

Как правило такие нагрузки обозначаются литерой q. Измеряются в Н/м или кгс/м.

В свою очередь распределенные нагрузки могут быть равномерно и неравномерно распределенными.

График, показывающий изменение значения распределенной нагрузки по длине балки, называется эпюрой нагрузки. Изменение значения распределенной нагрузки может описываться различными уравнениями. Например, для балки, на которую действует равномерно распределенная нагрузка, эпюра нагрузки имеет вид прямоугольника, а уравнение, описывающее изменение значений нагрузки, имеет следующий вид:

q = const (517.2)

Если одна или несколько нагрузок направлены не перпендикулярно оси х, а под некоторым углом а, то для дальнейших расчетов такие нагрузки разбиваются на вертикальную и горизонтальную составляющие.

Вертикальные составляющие используются для расчета балки на поперечный изгиб. Горизонтальные составляющие используются для определения горизонтальных опорных реакций, а также при необходимости для расчетов на устойчивость сжатого стержня.

Определить значение вертикальных и горизонтальных составляющих нагрузки можно по следующим формулам:

Q_в = Qsina (517.3)

Q_г = Qcosa (517.4)

1.4.3. Моментов

Внешний момент, действующий в любой точке по оси х, рассматривается как пара сил, равных по значению и направленных в противоположные стороны. Таким образом значение внешнего момента не зависит от расстояния до какой либо точки по оси х, а только от расстояния между векторами двух противоположно направленных сил.

Примечание: иногда при расчете балок бывает известен угол поворота или перемещение поперечного сечения. По большому счету ни угол поворота, ни перемещение не являются нагрузками, а есть результат воздействия нагрузок. Поэтому в таких случаях перемещения или углы поворота поперечных сечений заменяются силами или моментами, которые вызывают эквивалентное рассматриваемому перемещение или угол поворота.

1.5. Степень статической неопределимости

Все балки с количеством пролетов более одного, являются статически неопределимыми. Но даже и однопролетные балки могут быть статически неопределимыми. Степень статической неопределимости s для балок с шарнирными опорами определяется следующим образом:

Каждая жесткая заделка добавляет одну степень статической неопределимости. При наличии жестких заделок статическая определимость s определяется следующим образом:

Рисунок 145.3.1

1.6. Замена опор опорными реакциями

На этом этапе расчета опоры, имеющиеся у балки, заменяются реактивными силами, получившими название «опорные реакции». Эти опорные реакции также являются внешними силами для балки. Главное отличие опорных реакций от нагрузок в том, что изначально опорные реакции в отличие от нагрузок не известны и их нужно вычислить.

1.7. Статическое равновесие системы

Из этого следуют первые два уравнения статического равновесия системы:

Третье уравнение статического равновесия применимо только для статически определимых балок с шарнирными опорами. Смысл его сводится к тому, что шарнирные опоры не препятствуют повороту стержня на опоре, а значит момент на такой опоре будет равен нулю, если балка бесконсольная. Если на консоль действует нагрузка, то момент на опоре определяется, как для обычной консольной балки.

Для бесконсольной балки третье уравнение статического равновесия будет иметь вид:

Если нагрузка распределена по длине балки, то сначала определяется суммарная нагрузка (площадь грузовой эпюры), при этом плечо действия равно расстоянию от центра тяжести эпюры нагрузки. Другими словами, сначала распределенная нагрузка приводится к сосредоточенной силе и эта условно сосредоточенная сила действует в центре тяжести эпюры нагрузки.

1.8. Определение опорных реакций

При расчете статически неопределимых балок сначала определяются значения опорных реакций на промежуточных шарнирных опорах, если используется метод нулевых перемещений на опорах (метод сил) или моменты на промежуточных шарнирных или крайних жестких опорах, если используется метод определения углов поворота на опорах (уравнения трех моментов).

При использовании уравнений трех моментов значение реакции на крайней опоре А определяется, исходя из условия:

1.9. Построение эпюр

После того, как определены значения опорных реакций, можно переходить непосредственно к определению напряжений в поперечных сечениях балки. Для этого строятся эпюры поперечных и продольных сил, эпюра моментов, углов поворота поперечных сечений и эпюра перемещений (прогибов).

Затем по эпюре моментов определяется самое нагруженное поперечное сечение балки, в этой точке на эпюре моментов максимальное значение, отрицательное или положительное, в данном случае не имеет значения. Затем для этого сечения определяются значения поперечных и нормальных сил по соответствующим эпюрам.

2 этап. Подбор сечения

Так как разные материалы имеют разные значения расчетных сопротивлений, то соответственно и требуемые параметры сечения для балок из различных материалов будут разными.

2.1. Определение материала балки и расчетного сопротивления материала

После того, как выбран материал для балки, определяются расчетные сопротивления материала изгибу R_и, сжатию R_c, растяжению R_р и т.п. по действующим нормативным документам или по данным производителя, если балка будет из стали.

Для балок из разнородных материалов сначала определяются параметры приведенного сечения. Суть приведенного сечения состоит в том, что рассматривается некое условное сечение материала обладающего равным сопротивлением, при этом ширина сечения для материала, обладающего большим расчетным сопротивлением увеличивается во столько раз, во сколько расчетное сопротивление одного материала больше расчетного сопротивления другого материала. Поэтому такое сечение и называется приведенным. Другими словами, если бы балка изготавливалась из одного материала, то именно так и должно было бы выглядеть поперечное сечение.

Для железобетонных балок, являющихся также балками из разнородных материалов, как правило в процессе расчета требуется дополнительно определить сечение арматуры. Возможные варианты расчета железобетонных балок рассмотрены отдельно.

2.2. Определение требуемого момента сопротивления

Требуемый момент сопротивления определяется, исходя из следующего условия:

2.3. Определение геометрических параметров сечения

2.3 Определение геометрических параметров сечения

Поперечное сечение балки может быть каким угодно: круглым, квадратным, прямоугольным, в виде швеллера, двутавра, круглой или прямоугольной трубы и т.д.

Как известно наиболее оптимальными являются сечения в виде двутавра, швеллера или квадратной трубы, именно такие сечения и принимаются для стальных балок.

Для железобетонных балок наиболее характерны прямоугольное и тавровое сечения. Впрочем, как уже говорилось, расчет железобетонных балок отличается от расчета обычных балок.

Для балок прямоугольного сечения требуемая высота сечения определяется по формуле:

(147.4)

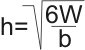
2.4. Определение прогиба

Так как для однопролетных балках на шарнирных опорах значение прогиба часто является определяющим, то я рекомендую определять прогиб сразу после определения параметров сечения.

Формулы для определения прогиба и углов поворота сечения на опорах зависят от вида приложенной к балке нагрузки. Значение модуля упругости E для выбранного материала балки определяется по нормативным документам, здесь можно посмотреть примерные значения модулей упругости для некоторых строительных материалов. Значение момента инерции I определяется в зависимости от геометрической формы сечения или по сортаменту для стальных балок из прокатного профиля.

Если прогиб f, определенный по одной из вышеуказанных формул, меньше допустимого нормативными документами, в частности СП 20.13330.2011 «Нагрузки и воздействия», то можно продолжать расчеты. Если прогиб больше допустимого, то сначала следует подобрать сечение, обеспечивающее требования по прогибу. Например для балки, на которую действует равномерно распределенная нагрузка, значение момента инерции можно определить по следующей формуле:

I = 5ql 4 /(384Ef) (517.9)

2.5. Проверка на прочность опорных участков балки

Любая балка в отличие от показанной на рисунке 219.2 модели имеет опорные участки. На этих опорных участках действуют нормальные напряжения в сечениях, параллельных нейтральной оси балки. В общем случае (если балка прямоугольная и напряжения на опорном участке равномерно изменяются от максимума до нуля) эти напряжения определяются по следующей формуле:

2.5.1. Проверка на прочность в местах действия сосредоточенной нагрузки

Так как на балку может действовать не только распределенная нагрузка, но и одна или несколько сосредоточенных нагрузок, то места действия сосредоточенных нагрузок также следует проверить на прочность.

В данном случае формула для определения нормальных напряжений будет будет почти такой же как (517.10), вот только значение коэффициента, учитывающего неравномерность распределения нагрузки, будет зависеть от того, как именно сосредоточенная нагрузка передается рассчитываемой балке.

Например, если рассчитываемая балка будет находиться посредине помещения и на нее сверху будет опираться второстепенная балка, то значение коэффициента будет равно 1.

2.6. Проверка по касательным напряжениям

В поперечных сечениях, соответствующих опорным точкам балки, а также в сечениях, параллельных нейтральной оси балки, будут действовать касательные напряжения, которые не должны превышать расчетного сопротивления R_s сдвигу или сколу:

Подобная проверка особенно важна для стальных тонкостенных балок.

2.7. Определение максимальных напряжений

Если в рассматриваемой точке (точнее на грани параллелепипеда с рассматриваемой точкой на одной из граней) действуют и нормальные и касательные напряжения, то возникает плоское напряженное состояние.

В этом случае необходимо определить максимальное нормальное напряжение, действующее в этой точке, другими словами определить главные площадки напряжений. Для этого используется одна из теорий прочности. Так, согласно третьей теории прочности:

σ_пр =(σ 2 +4т 2 ) 0.5 ≤ R (517.11)

Если на 4 из 6 главных площадок напряжений в области рассматриваемой точки действуют нормальные и касательные напряжения (например в местах приложения сосредоточенных нагрузок или на промежуточных опорах многопролетных балок), то значение максимальных нормальных напряжений составит:

Эта формула следует из общих положений теории сопротивления материалов, однако для стальных балок нормативные документы требуют проводить расчет по несколько другой формуле.

Кроме того в некоторых случаях, если отсутствуют опорные связи из плоскости балки (что в малоэтажном строительстве встречается крайне редко) тонкостенные стальные балки открытого профиля, а также деревянные балки любого сечения следует проверить на устойчивость в сжатой зоне сечения, но это уже совсем другая история.

Вот собственно и все, что имеет отношение к расчету балок.

Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»

Для терминалов номер Яндекс Кошелька 410012390761783

Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV

Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).

Источник