что такое побитовая упаковка
Битовые поля
Битовое поле — в программировании число, занимающее некоторый набор битов, напрямую не адресуемый процессором. Например: при 8-битном байте первые два поля протокола
Обращение к битовым полям требует дополнительных команд процессора для маскирования и сдвига, и потому медленнее обращений к словам/байтам. Поэтому битовые поля применяются для максимально полной упаковки информации в местах, где неважна скорость доступа к информации.
Компиляторы, как правило, ограничивают работу с битовыми полями только извлечением значения битового поля и записью значения в битовое поле, а само битовое поле воспринимается как беззнаковое число. Реальный порядок следования битовых полей в структуре есть системно-зависимым: в одних компиляторах битовые поля могут быть расположены начиная с младших битов, а в других — со старших.
Содержание
Операции над многобитовыми полями
Пусть в одном байте находятся три битовых поля: 1-битовые a и b, 2-битовое c и 4-битовое d, то есть 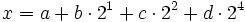
Сборка одного числа из битовых полей
Двоичные компьютеры обычно имеют команды побитового сдвига, которые позволяют быстро умножать на степени двойки — 2, 4, 8 и т. д. Вместо сложения можно применить команду логического «ИЛИ». Таким образом, число x можно собрать и по-другому:
Извлечение битового поля
Для извлечения битового поля нужно провести две операции:
Для младшего поля побитовый сдвиг не нужен, то есть:
Для старшего поля побитовый сдвиг сам по себе, без умножения на маску, очистит x от ненужных битов — то есть,
Замена битового поля
Например, если нам нужно заменить d, то
Операции над однобитовыми полями
Поля a и b имеют длину 1 бит — это позволяет работать с ними несколько другими средствами.
Проверка отдельного бита
Для проверки надо побитово умножить x операцией «И» на маску, у которой одна единица — в соответствующей позиции. Если получился 0, бит равен 0.
Проверка, равен ли единице хотя бы один бит из нескольких:
Проверка, равны ли единице все биты из нескольких:
Установка битов
Для этого надо сложить операцией «ИЛИ» x с маской, у которой единицы в соответствующих позициях. Например, чтобы включить бит a:
Чтобы включить и a, и b:
Снятие битов
Чтобы снять один или несколько битов, надо сложить x операцией «И» с маской, у которой в соответствующих позициях нули. В частности, чтобы выключить бит b, нужно дать команду:
Переключение битов
Для переключения битов (с 0 на 1, с 1 на 0) надо сложить x командой «Исключающее ИЛИ» с маской, у которой в соответствующих позициях единицы. Например, бит b переключается так:
Операции над знаковыми полями в дополнительном коде
Существуют два способа хранения отрицательных целых чисел — знаковый бит и дополнительный код. В подавляющем большинстве современных машин применяется второй. При записи отрицательных чисел дополнительным кодом имеем:
Считаем, что поля c и d имеют именно такой формат. Тогда поле c может хранить числа от −2=102 до 1=012, а поле d — от −8=10002 до 7=01112.
Сборка и замена чисел
Каждое из слагаемых (кроме старшего), чтобы оно не испортило более старшие разряды, требуется умножать на битовую маску соответствующей длины. В частности:
Извлечение чисел
Для извлечения чисел требуется сдвинуть поле на нужное количество битов вправо, заодно размножив знаковый бит. Например, для этого можно воспользоваться арифметическим сдвигом. Если x имеет длину 8 битов, то
Если арифметического сдвига нет, то…
Полезное
Смотреть что такое «Битовые поля» в других словарях:
Поле класса — или атрибут (переменная член, data member, class field, instance variable) в объектно ориентированном программировании переменная, связанная с классом или объектом. Все данные объекта хранятся в его полях. Доступ к полям осуществляется по… … Википедия
Битовое поле — Битовое поле в программировании число, занимающее некоторый набор битов, напрямую не адресуемый процессором. Например: при 8 битном байте первые два поля протокола IP версия и IHL будут битовыми полями. На машинах с 32 битным… … Википедия
D (язык программирования) — У этого термина существуют и другие значения, см. D. D Семантика: мультипарадигменный: императивное, объектно ориентированное, обобщённое программирование Тип исполнения: компилятор Появился в: 1999 Автор(ы) … Википедия
ARINC 429 — стандарт на компьютерную шину для применения в авионике. Разработан фирмой ARINC. Стандарт описывает основные функции и необходимые физические и электрические интерфейсы для цифровой информационной системы самолёта. Сегодня, ARINC 429 является… … Википедия
Автоматное программирование — Автоматное программирование это парадигма программирования, при использовании которой программа или её фрагмент осмысливается как модель какого либо формального автомата. В зависимости от конкретной задачи в автоматном программировании… … Википедия
Дополнительный код (представление числа) — У этого термина существуют и другие значения, см. Дополнительный код. Дополнительный код (англ. two’s complement, иногда twos complement) наиболее распространённый способ представления отрицательных целых чисел в компьютерах. Он позволяет… … Википедия
8-битный цвет — Глубина цвета битовое изображение 8 битная шкала серого 8 битный цвет 15/16 bit: Highcolor 24 bit: Truecolor 30/36/48 bit: Deep Color См. также Цветовая модель RGB Цветовая модель CMYK Цветовая палитра Видимое излучение Цвета в Web (Цвета HTML) 8 … Википедия
ExFAT — Разработчик Microsoft Файловая система Расширенная таблица размещения файлов (англ. Extended File Allocation Table) Дата представления Ноябрь 2006 (Windows Embedded CE 6.0) Метка тома 0x07 (MBR) EBD0A0A2 B9E5 4433 87C0 68B6B72699C7 (GP … Википедия
exFAT — Разработчик Microsoft Файловая система Расширенная таблица размещения файлов (англ. Extended File Allocation Table) Дата представления Ноябрь 2006 (Windows Embedded CE 6.0) Метка тома 0x07 (MBR) EBD0A0A2 B9E5 4 … Википедия
Битовое поле
Битовое поле — в программировании число, занимающее некоторый набор битов, напрямую не адресуемый процессором. Например: при 8-битном байте первые два поля протокола IP — версия и IHL — будут битовыми полями. На машинах с 32-битным байтом все поля IP-пакета (кроме IP-адресов отправителя и получателя) будут битовыми.
Обращение к битовым полям требует дополнительных команд процессора для маскирования и сдвига, и потому медленнее обращений к словам/байтам. Поэтому битовые поля применяются для максимально полной упаковки информации в местах, где не важна скорость доступа к информации.
Компиляторы, как правило, ограничивают работу с битовыми полями только извлечением значения битового поля и записью значения в битовое поле, а само битовое поле воспринимается как беззнаковое число. Реальный порядок следования битовых полей в структуре является системно-зависимым: в одних компиляторах битовые поля могут быть расположены начиная с младших битов, а в других — со старших.
Содержание
Операции над многобитовыми полями
Пусть в одном байте находятся три битовых поля: 1-битовые a и b, 2-битовое c и 4-битовое d, то есть 
Сборка одного числа из битовых полей
Двоичные компьютеры обычно имеют команды побитового сдвига, которые позволяют быстро умножать на степени двойки — 2, 4, 8 и т. д. Вместо сложения можно применить команду логического «ИЛИ». Таким образом, число x можно собрать и по-другому:
Извлечение битового поля
Для извлечения битового поля нужно провести две операции:
Для младшего поля побитовый сдвиг не нужен, то есть:
Для старшего поля побитовый сдвиг сам по себе, без умножения на маску, очистит x от ненужных битов — то есть,
Замена битового поля
Например, если нам нужно заменить d, то
Операции над однобитовыми полями
Поля a и b имеют длину 1 бит — это позволяет работать с ними несколько другими средствами.
Проверка отдельного бита
Для проверки надо побитово умножить x операцией «И» на маску, у которой одна единица — в соответствующей позиции. Если получился 0, бит равен 0.
Проверка, равен ли единице хотя бы один бит из нескольких:
Проверка, равны ли единице все биты из нескольких:
Установка битов
Для этого надо сложить операцией «ИЛИ» x с маской, у которой единицы в соответствующих позициях. Например, чтобы включить бит a:
Чтобы включить и a, и b:
Снятие битов
Чтобы снять один или несколько битов, надо сложить x операцией «И» с маской, у которой в соответствующих позициях нули. В частности, чтобы выключить бит b, нужно дать команду:
Переключение битов
Для переключения битов (с 0 на 1, с 1 на 0) надо сложить x командой «Исключающее ИЛИ» с маской, у которой в соответствующих позициях единицы. Например, бит b переключается так:
Операции над знаковыми полями в дополнительном коде
Существуют два способа хранения отрицательных целых чисел — знаковый бит и дополнительный код. В подавляющем большинстве современных машин применяется второй. При записи отрицательных чисел дополнительным кодом имеем:
Считаем, что поля c и d имеют именно такой формат. Тогда поле c может хранить числа от −2=102 до 1=012, а поле d — от −8=10002 до 7=01112.
Сборка и замена чисел
Каждое из слагаемых (кроме старшего), чтобы оно не испортило более старшие разряды, требуется умножать на битовую маску соответствующей длины. В частности:
Извлечение чисел
Для извлечения чисел требуется сдвинуть поле на нужное количество битов вправо, заодно размножив знаковый бит. Например, для этого можно воспользоваться арифметическим сдвигом. Если x имеет длину 8 битов, то
Внимание! В языке программирования Java всё наоборот: знаком >> обозначается арифметический сдвиг, знаком >>> — простой.
Если арифметического сдвига нет, то…
Объявления битовых полей
В языке C/C++
В декларации битового поля используется двоеточие, за которым следует константное выражение определяющее количество битов в поле [1] ;
Примечания
Полезное
Смотреть что такое «Битовое поле» в других словарях:
битовое поле — Смежные биты или октеты в кодовой последовательности, которые декодируются как целое и которые либо представляют абстрактное значение, либо содержат информацию, необходимую для успешного декодирования, либо представляют то и другое. Примечание… … Справочник технического переводчика
дополнительное битовое поле — Битовое поле, которое иногда вставляется (для кодирования абстрактного значения), а иногда опускается (МСЭ Т Х.692). [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN optional bit field … Справочник технического переводчика
Поле (значения) — Поле многозначное понятие, связанное с протяжённостью в пространстве: Понятие в математике Поле алгебраическая структура с двумя операциями. Скалярное, векторное и тензорное поля в дифференциальной геометрии (см. вектор и тензор) и матанализе … Википедия
Поле (информатика) — Поле многозначное понятие, связанное с протяжённостью в пространстве: Понятие в математике Поле алгебраическая структура с двумя операциями. Скалярное, векторное и тензорное поля в дифференциальной геометрии (см. вектор и тензор) и матанализе … Википедия
поле маршрутной информации — Битовое поле, содержащее маршрутную информацию. [http://www.lexikon.ru/dict/net/index.html] Тематики сети вычислительные EN routing information fieldRIF … Справочник технического переводчика
Поле — Поле многозначное понятие, связанное с протяжённостью в пространстве: поле в Викисловаре … Википедия
Битовые поля — Битовое поле в программировании число, занимающее некоторый набор битов, напрямую не адресуемый процессором. Например: при 8 битном байте первые два поля протокола Обращение к битовым полям требует дополнительных команд процессора для… … Википедия
Сетевое кодирование — Для термина «Кодирование» см. другие значения. Сетевое кодирование раздел теории информации изучающий вопрос оптимизации передачи данных по сети с использованием техник изменения пакетов данных на промежуточных узлах. Содержание 1 Основы… … Википедия
Побитовая арифметика в Java
Приветствую, дорогой читатель.
Редко, но все же задачки из собеседований и обучалок имеют практическую ценность. Так, мне понадобилось реализовать на Java альтернативу арифметическим операциям над целочисленными значениями. Благо, первые страницы поисковиков пестрят готовыми решениями побитовых аналогов, и над большинством из них голову ломать не пришлось.
Признаться, я был несколько удивлен отсутствию такого материала на Хабре (плохо искал?), потому и решил восполнить этот недостаток, со своими комментариями и дополнениями.
Прошу учесть, что в примерах с побитовыми операциями значения урезаны до полубайта: фундаментальной разницы не будет, а воспринимается легче.
Сложение
Для начала надо вспомнить о переносе в старший разряд. В десятичной системе под его определение (для текущего разряда) подпадают значения в диапазоне от 10 до 18:
В двоичной же системе переносится все, что больше единицы:
В последнем примере первыми складываются самые младшие биты:
Ноль остается в текущем разряде, а единица переходит в старший, где участвует в сложении:
младшая единица остается в текущем, старшая сдвигается дальше. Отсюда же можно вывести правило, что в двоичной системе для одного текущего разряда под перенос подпадают значения от двух до трех включительно.
В части, касающейся алгоритма, стоит обратить внимание на инструкцию определения наличия/отсутствия переноса на примере предыдущих значений:
Это еще не перенос, но выставление «флагов» над разрядами, сложение которых оставляет перенос, т.е. перенос при сложении — это когда биты одинаковые.
Коль скоро уже что-то да прояснилось, то теперь первое слагаемое должно быть освобождено от битов, по которым перенос учтен:
Как известно, побитовый оператор «Исключающее ИЛИ» выставит биты только если значения разрядов противоположны.
Третий шаг цикла — это преобразование «флагов» наличия переноса непосредственно в перенос. Для этого они сдвигаются на один шаг влево и присваиваются второму слагаемому:
На последующей итерации перенос зафиксирован не будет, т.к:
Второй шаг даст нам:
Что является искомой суммой, а третий шаг завершит цикл while():
Вычитание
Эквивалентен предыдущему с той лишь разницей, что заем битов у старших разрядов реализован инверсия обратной импликации. Ну и переименовываем локальные переменные.
Умножение
Вернемся к истокам: умножение в столбик в десятичной системе:
т.е. мы перемножаем каждый разряд второго множителя с первым множителем. Отсюда же следует, что произведение от старшего разряда сдвигается на один шаг влево. И наконец складываем промежуточные значения. То же самое происходит на побитовом уровне:
Делаем вывод, что алгоритм только и должен, что складывать первый множитель с самим собою всякий раз как во втором множителе встречается установленный бит, естественно, с учетом правила перевода в старший разряд:
Дальше осуществляется сдвиг первого множителя на один разряд влево (формируем «лесенку»):
Теперь определяем, есть ли бит во втором по значимости разряде второго множителя:
Цикл работает до тех пор, пока второй множитель не равен нулю. Хотел бы обратить внимание на следующее: от ресурса к ресурсу гуляет экземпляр этого алгоритма, где логический сдвиг второго множителя (mul2 >>>= 1) заменен на арифметический (mul2 >>= 1). Вероятно, он берет свое начало из реализации на C/C++, где есть ключевое слово unsigned и такая подмена не является проблемой. Однако в Java все типы чисел знаковые и если второй множитель будет представлен отрицательным значением, то такая оплошность приведет к вываливанию алгоритма в бесконечный цикл, т.к. второй множитель всегда будет отвечать его условию:
Деление
С делением вышло не так гладко, как с предыдущими примерами: пришлось писать велосипед (сильно не бить).
Деление — это вычитание делителя от делимого до тех пор, пока частное больше или равно нулю. При таком подходе достаточно определить счетчик, значение которого инкрементируется после каждой операции вычитания. Его итоговое значение и есть частное:
Недостаток такого подхода становится особенно ощутимым при подаче устройству с ограниченными ресурсами последовательности из инструкций, как то: 2147483647 / 1; 2147483647 / 2; 2147483647 / 3, сложится впечатление, что приложение зависло.
Куда эффективней была бы работа на уровне битов. Но единственное найденное решение имеет тот недостаток, что для корректного вывода требуется тип переменных, на ступень выше охватываемого диапазона, т.е. если на вход подаете short, то тип локальных переменных должен быть int, иначе результат деления больших значений будет удивлять. В моем случае ситуация усугублялась отсутствием типа long.
Но вернемся к нашим баранам.
Для понимания принципа работы алгоритма необходимо вспомнить порядок деления столбиком:
Вот тут по-подробней. На выхлопе у нас получилось следующее: мы «вытолкнули» делитель влево до того разряда, где он минимизировал разность с делимым:
Этот механизм реализован в алгоритме. В цикле while() делитель должен сдвигаться влево до тех пор, пока не будет удовлетворять вышеописанному правилу. Параллельно с ним сдвигается маска частного. Оператор ветвления if() гласит: «сдвинуть можно если только результат этой операции не нарушит основное правило». Дополнительная проверка на отрицательное число связана с тем, что в Java выставленный самый старший бит – это отрицательное число. Без него цикл упадет в бесконечность:
Как только алгоритм перестал отвечать условиям if(), код входит в else, где на частном устанавливается бит маски:
Это аналогично выставлению битов при делении столбиком. Затем от делимого вычитается делитель:
После этого делитель и маска возвращаются в исходное состояние и цикл начинается вновь:
Напоследок хотел бы добавить несколько слов о дополнительном коде.
Приведенный алгоритм предполагает деление только положительных чисел, которые получены дополнительным кодом:
Тут происходит следующее: если число отрицательное, то его биты инвертируются, а результат складывается с единицей и получаем положительное (абсолютное) значение. Это же правило действительно для положительных чисел, например:
Но есть одно исключение — это максимально большое отрицательное число заданного типа, например:
Для чего нужны побитовые операции?
Для чего битовые сдвиги вообще существуют? А потому, что они выполняются очень простой схемой — сдвиговым регистром. И вместо того, чтобы проводить умножение (поначалу это было десятки тактов), подключаем этот самый регистр к регистрам процессора, и выполним всё за один такт. Существовала даже программа, генерирующая быстрый код умножения на константу, например, 6 — сдвинуть, сложить и ещё раз сдвинуть. И это в своё время было быстрее, чем mul — а ведь сейчас мы без зазрения совести пишем mul eax, 6.
Чего могут сдвиги, но со скрипом реализуется через всё остальное? Доступ к i-му биту.
i-й бит = (x >> i) & 1
По правилам хорошего программистского тона умножение, даже на 2 или на 4, пишется как обычное * (>> пишут, если компилятор непроходимо туп и умножение медленнее). А вот сдвиги — именно их, а не умножение — пишут, когда работают с битовыми полями.
Есть также специальные сдвиги.
* Арифметический сдвиг вправо (левый совпадает с обычным) — для чисел со знаком.
* Сдвиг-вращение — в основном для криптографии.
* Сдвиг-вращение через регистр флагов — в основном для длинной арифметики.
Побитовые операции нужня для того, что бы менять отдельные биты в значениях. По большей части, если не брать в расчет быстрые алгоритмы, то чаще всего побитовые операции необходимы для работы с масками. Частенько при помощи оных задают какие-то флаги, или как указал Человек я та же маска подсети зная которую и зная IP адрес текущей машины можно узнать IP адрес хоста и весь диапозон IP адресов сети за счет банальной операции побитового и. Есть еще задачи связанные с кодированием информации, есть бит/байт стаффинг, упаковка данных (привет сдвиги) и т.д.
Словом без побитовых операций тяжко бы пришлось и тогда стало бы невозможно скажем при помощи FileApi открыть какой-то бинарный формат данных на клиенте.
Битовые операции
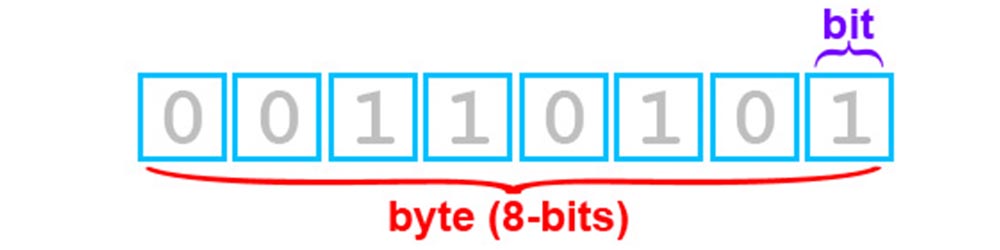
Данный урок основан на оригинальном уроке по битовым операциям от Arduino, можете почитать его здесь – там всё описано чуть более подробно.
Двоичная система и хранение данных
| 2 в степени | DEC | BIN |
| 0 | 1 | 0b00000001 |
| 1 | 2 | 0b00000010 |
| 2 | 4 | 0b00000100 |
| 3 | 8 | 0b00001000 |
| 4 | 16 | 0b00010000 |
| 5 | 32 | 0b00100000 |
| 6 | 64 | 0b01000000 |
| 7 | 128 | 0b10000000 |
Таким образом, степень двойки явно “указывает” на номер бита в байте, считая справа налево (примечание: в других архитектурах может быть иначе). Напомню, что абсолютно неважно, в какой системе исчисления вы работаете – микроконтроллеру всё равно и он во всём видит единицы и нули. Если “сложить” полный байт в десятичном представлении битов, то мы получим как раз 255: 128+64+32+16+8+4+2+1 = 255. Нетрудно догадаться, что число 0b11000000 равно 128+64, то есть 192. Именно таким образом и получается весь диапазон от 0 до 255, который умещается в один байт. Если взять два байта – будет всё то же самое, просто ячеек будет 16, то же самое для 4 байт – 32 ячейки с единицами и нулями, каждая имеет свой номер согласно степени двойки. Давайте начнём манипуляции с битами с самого простого – с макро-функций, которые идут “в комплекте” с ядром Arduino.
Макросы для манипуляций с битами
В “библиотеке” Arduino.h есть несколько удобных макросов, которые позволяют включать и выключать биты в байте:
| Макросы Arduino.h | Действие |
| bitRead(value, bit) | Читает бит под номером bit в числе value |
| bitSet(value, bit) | Включает (ставит 1) бит под номером bit в числе value |
| bitClear(value, bit) | Выключает (ставит 0) бит под номером bit в числе value |
| bitWrite(value, bit, bitvalue) | Ставит бит под номером bit в состояние bitvalue (0 или 1) в числе value |
| bit(bit) | Возвращает 2 в степени bit |
| Другие встроенные макросы | |
| _BV(bit) | Возвращает 2 в степени bit |
| bit_is_set(value, bit) | Проверка на включенность (1) бита bit в числе value |
| bit_is_clear(value, bit) | Проверка на выключенность (0) бита bit в числе value |
Битовые операции
Переходим к более сложным вещам. На самом деле они максимально просты для микроконтроллера, настолько просты, что выполняются за один такт. При частоте 16 МГц (большинство плат Arduino) одна операция занимает 0.0625 микросекунды.
Битовое И
И (AND), оно же “логическое умножение”, выполняется оператором & или and и возвращает следующее:
Основное применение операции И – битовая маска. Позволяет “взять” из байта только указанные биты:
То есть при помощи & мы взяли из байта 0b11001100 только биты 10000111, а именно – 0b11001100, и получили 0b10000100 Также можно использовать составной оператор &=
Битовое ИЛИ
ИЛИ (OR), оно же “логическое сложение”, выполняется оператором | или or и возвращает следующее:
Основное применение операции ИЛИ – установка бита в байте:
Также можно использовать составной оператор |=
Вы уже поняли, что указывать на нужные биты можно любым удобным способом: в бинарном виде (0b00000001 – нулевой бит), в десятичном виде (16 – четвёртый бит) или при помощи макросов bit() или _BV() ( bit(7) даёт 128 или 0b10000000, _BV(7) делает то же самое)
Битовое НЕ
Битовая операция НЕ (NOT) выполняется оператором
и просто инвертирует бит:
Также она может инвертировать байт:
Битовое исключающее ИЛИ
Битовая операция исключающее ИЛИ (XOR) выполняется оператором ^ или xor и делает следующее:
Данная операция обычно используется для инвертирования состояния отдельного бита:
То есть мы взяли бит №7 в байте 0b11001100 и перевернули его в 0, получилось 0b01001100, остальные биты не трогали.
Битовый сдвиг
Битовый сдвиг делает не что иное, как умножает или делит байт на 2 в степени. Да, это операция деления, выполняющаяся за один такт процессора! К этому мы ещё вернёмся ниже. Посмотрите на работу оператора сдвига и сравните её с макросами bit() и _BV() :
Включаем-выключаем
Вспомним пример из пункта про битовое ИЛИ, про установку нужного бита. Вот эти варианты кода делают одно и то же:
Как насчёт установки нескольких бит сразу?
Или прицельного выключения бит? Тут чуть по-другому, используя &= и
Выключить несколько бит сразу? Пожалуйста!
Именно такие конструкции встречаются в коде высокого уровня и библиотеках, именно так производится работа с регистрами микроконтроллера. Вернёмся к устройству Ардуиновских макросов:
Я думаю, комментарии излишни: макросы состоят из тех же элементарных битовых операций и сдвигов!
Быстрые вычисления
Как я уже говорил, битовые операции – самые быстрые. Если требуется максимальная скорость вычислений – их можно оптимизировать и подогнать под “степени двойки”, но иногда компилятор делает это сам, подробнее смотри в уроке про оптимизацию кода. Рассмотрим базовые операции:
Примечание: рассмотренные выше операции работают только с целочисленными типами данных!
Экономия памяти
При помощи битовых операций можно экономить немного памяти, пакуя данные в блоки. Например, переменная типа boolean занимает в памяти 8 бит, хотя принимает только 0 и 1. В один байт можно запаковать 8 логических переменных, например вот так:
Ещё интересный пример сжатия
Таким образом мы отброс или у красного и синего младшие (правые) биты, в этом и заключается сжатие. Чем больше битов отброшено – тем менее точно получится “разжать” число. Например сжимали число 0b10101010 (170 в десятичной) на три бита, при сжатии получили 0b10101000, т.е. потеряли три младших бита, и в десятичной уже получится 168. Для упаковки используется битовый сдвиг и маска, таким образом мы берём первые пять битов красного, шесть зелёного и пять синего, и задвигаем на нужные места в результирующей 16-битной переменной. Всё, цвет сжат и его можно хранить. Для распаковки используется обратная операция: выбираем при помощи маски нужные биты и сдвигаем их обратно в байт:
Как и в примере со светодиодами, мы просто брали нужные биты ( в этом случае младшие два, 0b11 ) и сдвигали их на нужное расстояние. Для распаковки делаем в обратном порядке:
И получим обратно наши байты. Также маску можно заменить на более удобную для работы запись, задвинув 0b11 на нужное расстояние:
Ну и теперь, проследив закономерность, можно сделать для себя функцию или макрос чтения пакета:
Где x это пакет, а y – порядковый номер запакованного значения. Выведем посмотрим:
“Трюки” с битами
На битовых операциях можно сделать очень много всего интересного, и работать оно будет очень быстро и занимать мало места. Огромный список битовых трюков и хаков можно посмотреть в этой статье, их там очень много и все с примерами. Есть ещё один небольшой сборник самых простых и полезных хаков вот здесь (английский). Его я перевёл, смотрите ниже под спойлером. Другой вариант перевода (могут быть не все трюки) можно посмотреть здесь.
Перемотка бита
Целые
Установка n го бита
Выключение n го бита
Инверсия n го бита
Округление до ближайшей степени двойки
Округление вниз
Получение максимального целого
Получение минимального целого
Получение максимального long
Умножение на 2
Деление на 2
Умножение на m ую степень двойки
Деление на m ую степень двойки
Остаток от деления
Проверка равенства
Проверка на чётность (кратность 2)
Обмен значениями
Получение абсолютного значения
Максимум из двух
Минимум из двух
Проверка на одинаковый знак
Смена знака
Вернёт 2 n
Является ли число степенью 2
Остаток от деления на 2 n на m
Среднее арифметическое
Получить m ый бит из n (от младшего к старшему)
Получить m ый бит из n (от старшего к младшему)
Проверить включен ли n ый бит
Выделение самого правого включенного бита
Выделение самого правого выключенного бита
Выделение правого включенного бита
Выделение правого выключенного бита
n + 1
n – 1
Получение отрицательного значения
if (x == a) x = b; if (x == b) x = a;
Поменять смежные биты
Different rightmost bit of numbers m & n
Common rightmost bit of numbers m & n
Десятичные дроби
Примечание: хаки с float могут не работать на Ардуино! Разбить float в массив бит (unsigned uint32_t)
Вернуть массив бит обратно в float
Быстрый обратный квадратный корень
Быстрый n ый корень из целого числа
Быстрая степень
Быстрый натуральный логарифм
Быстрая экспонента
Строки
Конвертировать в нижний регистр
Конвертировать в верхний регистр
Инвертировать регистр
Позиция буквы в алфавите (англ)
Позиция большой буквы в алфавите (англ)
Позиция строчной буквы в алфавите (англ)
Другое
Быстрая конвертация цвета R5G5B5 в R8G8B8
Приоритет операций
Чтобы не плодить скобки, нужно знать приоритет операций. В C++ он такой:
