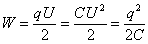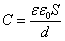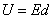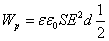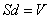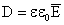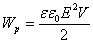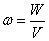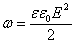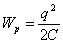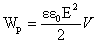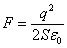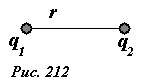что такое плотность энергии
Объемная плотность энергии магнитного и электрического полей
Электрическое поле и его свойства
Заряженные тела окружены особой средой, которая представляет собой электрическое поле. С его помощью осуществляется электрическое взаимодействие.
Электрическое поле — физическое поле, окружающее любой электрический заряд и оказывающее силовое воздействие на другие заряды, отталкивая или притягивая их.
Причинами возникновения электрического поля служат:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Электрические и магнитные поля принято рассматривать в качестве проявления обобщенного электромагнитного поля. Данное понятие связано с проявлением какого-либо из четырех фундаментальных взаимодействий природного характера.
Изучение и применение свойств электрических полей имеет большое значение в развитии физики как науки. На основе электрических полей разрабатывают электротехническое оборудование. С точки зрения атомной физики и химии, электрическое поле является силой удержания атомного ядра и электронов в атомах.
За счет данной силы формируются химические связи между атомами, что приводит к образованию молекул. Путем практического применения электрических полей удается обнаружить движения с помощью емкостных методик. Явление активно используют в диагностике и терапии в медицинской сфере.
У электрического поля есть математическое определение, согласно которому оно представляет собой векторное поле, связывающее с любой точкой в пространстве силу (электростатическую или кулоновскую) на единицу заряда, приложенную к бесконечно малому положительному пробному заряду, покоящемуся в этой точке.
В системе СИ единица измерения электрического поля: Вольт на метр (В/м), что в точности эквивалентно Ньютону на Кулон (Н/Кл).
Электрическое поле обладает следующими свойствами:
С целью раскрытия смысла понятия «электрического поля» можно рассмотреть основные его характеристики.
Напряженность — силовая характеристика электрического поля.
Напряженность, как векторная величина, обозначается Е и измеряется в Ньютонах на Кулон (Н/Кл), либо Вольтах на метр (В/м).
Найти напряженность можно по формуле:
Силовые линии — линии, касательные к которым совпадают с вектором напряженности.
Свойства силовых линий:
Электрические заряды, которые являются причиной образования электрических полей, описывают с помощью закона Гаусса. Электрические поля могут быть сформированы за счет изменения магнитных полей. В этом случае работает закон электромагнитной индукции Фарадея.
Перечисленные закономерности позволяют определить поведение электрического поля в вакуумной среде. С другой стороны, магнитное поле представляет собой функцию электрического поля. Можно выявить связь между уравнениями для обоих полей. В результате будут образованы уравнения Максвелла, описывающие магнитное и электрическое поля в виде функции зарядов и токов.
При рассмотрении частного случая стационарного состояния, то есть при наличии стационарных зарядов и токов, можно наблюдать исчезновение индуктивного эффекта Максвелла–Фарадея. Получается пара уравнений.
Закон Фарадея без индукционного члена:
\(\displaystyle \nabla \times \mathbf
\(\varepsilon _ <0>\) — электрическая постоянная.
Анализируя записанное уравнение можно сделать вывод: электрическое поле, создающее точечный заряд, в любом месте имеет направление от заряда в том случае, когда он положительный. Если заряд отрицательный — поле направлено в его сторону. Можно также заметить уменьшение величины поля пропорционально обратному квадрату расстояния от заряда.
Кулоновская сила, которая действует на заряд величиной q в какой-либо точке пространства, определяется, как произведение заряда и электрического поля в этой точке:
Уравнения Максвелла линейны. По этой причине для электрических полей характерен принцип суперпозиции. Согласно данной закономерности, полное электрическое поле в точке от распределенных в пространстве зарядов соответствует векторной сумме электрических полей, которые образованы в рассматриваемой точке отдельными зарядами.
Запись результирующего поля с помощью закона Кулона:
С помощью принципа суперпозиции можно выполнить расчет электрического поля от непрерывного распределения \(<\displaystyle \rho (<\boldsymbol
С учетом заряда \(<\displaystyle \rho (<\boldsymbol
Рассчитать полное электрическое поле можно с помощью суммы вкладов от всех малых объемов. При этом нужно воспользоваться методом интегрирования по объему распределения заряда \(<\displaystyle \rho (x')>\) :
В том случае, когда рассматривается статичная система с магнитными полями, стабильными во времени, согласно закону Фарадея, электрическое поле является потенциальным. При этом допустимо задать электрический потенциал или функцию \(\Phi.\) В результате:
Общий случай электрического поля недопустимо описывать без учета магнитного поля. При зависимости от вектора магнитного потенциала A, определенного как:
допустимо записать электрический потенциал \( <\displaystyle \Phi >\) в виде:
где \( <\displaystyle \nabla \Phi >—\) градиент электрического потенциала;
Из рассмотренного уравнения можно получить закон индукции Фарадея:
Плотность энергии электрического и магнитного полей
Энергия электромагнитного поля — энергия, которая заключена в электромагнитном поле.
В рамках данного понятия можно рассматривать частные случаи чистого электрического и чистого магнитного поля. Рассмотреть энергию электромагнитного поля допустимо с помощью его характеристик.
Работа A электрического поля E, которая совершается для перемещения заряда Q, схожа по смыслу с механической работой:
где \(U=\int E\,dx\) — разность потенциалов, или напряжение.
Чаще всего при решении примеров рассматривают непрерывный перенос заряда за определенное время между точками с конкретной разностью потенциалов U(t). В результате уравнение для определения работы принимает следующий вид:
Мощность P, которая характеризует электрический ток на отрезке цепи, равна производной от работы A по времени. Формула для расчета мощности:
Согласно закону Ома:
Электрическая мощность, которая выделяется на сопротивлении R, определяется, как:
Формула мощности с учетом напряжения принимает следующий вид:
Таким образом, работа (выделившаяся теплота) представляет собой интеграл мощности по времени:
Если рассматривать электрическое и магнитное поля, можно прийти к выводу, что их энергия пропорциональна квадрату напряженности поля. Определение «энергия электромагнитного поля» не совсем соответствует действительности. Ему на замену в физике нередко употребляют термин плотности энергии электромагнитного поля (в заданной точке пространства). Общая величина энергии поля является интегралом плотности энергии по всему пространству.
В вакуумной среде и микрополях:
где E — напряженность электрического поля;
B — магнитная индукция;
D — электрическая индукция;
H — напряженность магнитного поля;
\(\varepsilon _ <0>\) — электрическая постоянная;
\(\mu _<0>\) — магнитная постоянная.
Энергия электромагнитного поля в колебательном контуре:
где U — электрическое напряжение в цепи;
C — электроемкость конденсатора;
L — индуктивность катушки или витка с током.
В том случае, когда речь идет об электромагнитной волне, плотность потока энергии определяют с помощью вектора Пойнтинга S (в русской научной литературе можно встретить понятие вектор Умова–Пойнтинга).
В системе СИ вектор Пойнтинга определяют, как:
В результате вектор Пойнтинга равен векторному произведению напряженностей электрического и магнитного полей. Направление вектора совпадает с перпендикулярами к векторам E и H. Данное условие соответствует свойству поперечности электромагнитных волн.
С другой стороны, формулу для плотности потока энергии можно адаптировать для случая стационарных электрических и магнитных полей:
Формула объемной плотности энергии
Конденсатор представляет собой двухполюсник, значение емкости которого может быть постоянным или переменным, а проводимость обладает малыми значениями.
Конденсатор является устройством, предназначенным для накопления заряда и энергии электрического поля, и пассивным электронным компонентом. Единицами измерения емкости конденсатора являются фарады.
Принято выражать энергию заряженного конденсатора с помощью величин, являющихся характеристиками электрического поля в пространстве между обкладками.
Энергия плоского конденсатора:
Емкость плоского конденсатора:
Таким образом, напряженность поля в конденсаторе и разность потенциалов между его обкладками связаны формулой:
С другой стороны, объем конденсатора равен:
С учетом \(\overrightarrow
Объемная плотность энергии электрического поля:
Объемная плотность энергии — величина, равная энергии единицы объема поля.
В случае изотропного диэлектрика объемная плотность энергии:
Исходя из записанных уравнений, можно сделать вывод о том, что плотность энергии поля с определенной напряженностью, образованного в среде с конкретной проницаемостью, прямо пропорциональна квадрату напряженности поля.
Энергия поля конденсатора с зарядом q на его обкладке определяется с помощью величины заряда и емкости конденсатора:
Энергия электрического поля может быть определена при известной силовой характеристике поля:
В том случае, когда поле является однородным:
Между обкладками плоского конденсатора действует сила притяжения. Известно, что:
Одна пластина создает поле, напряженность которого равна:
Записанное выражение не согласуется с опытом. Причина заключается в том, что кроме «электрической силы» на обкладки со стороны диэлектрика (имеется виду жидкий или газообразный диэлектрик) действуют еще механические силы, стремящиеся их раздвинуть. Опытным путем доказано, что роль носителя энергии играет поле.
В электростатике поле и заряды невозможно отделить друг от друга. С другой стороны, электрические поля, которые изменяются по времени, могут существовать обособлено, независимо от возбудивших их зарядов, и могут распространяться в пространстве в виде электромагнитных волн, способных переносить энергию.
Единицы измерения плотности энергии
Учебники
Журнал «Квант»
Общие
§9. Электрическое поле и его свойства
9.13 Энергия электрического поля. Плотность энергии.
Вернемся к обсуждению вопроса об энергии взаимодействия электрических зарядов. Ранее мы показали, что потенциальная энергия электростатического взаимодействия двух точечных зарядов q1 и q2, находящихся на расстоянии r друг от друга (рис. 212), рассчитывается по формуле
Придадим этой формуле несколько иной вид
В этой формуле мы выписали два равных слагаемых, каждое из которых можно трактовать как энергию взаимодействия одного из зарядов с другим, но мы подчеркивали, что энергия взаимодействия, не «принадлежит» ни одному из зарядов, поэтому нельзя учитывать эту энергию дважды – из-за этого и появляется в формуле множитель 1/2.
Использование понятия энергии взаимодействия требует чрезвычайной точности и внимательности. Произвол в выборе нулевого уровня энергии, с одной стороны, предоставляет определенную свободу, а, с другой, требует четкого понимания о какой именно энергии идет речь. Так, если в формуле (3) потенциалы отсчитываются относительно точек, бесконечно удаленных от зарядов, то эта формула определяет работу, которую совершит электрическое поле при удалении всех зарядов на бесконечно большие расстояния друг от друга. Если же требуется рассчитать работу поля при изменении положения зарядов, то выбор нулевого уровня не принципиален – эта работа не зависит от нулевого уровня потенциала.
Для того чтобы разобраться в некоторых нюансах применения формулы (3), рассмотрим примеры расчета энергии электростатического взаимодействия.
Три точечных заряда.
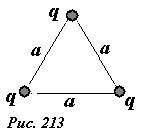
Пусть три одинаковых точечных заряда, величины которых равны между собой q1 = q2 = q3 = q, расположены в вершинах правильного треугольника со стороной a (рис.213). Для расчета энергии взаимодействия этих зарядов заметим, что все заряды равноправны, находятся в одинаковых условиях. В месте расположения одного из зарядов потенциал поля, создаваемого двумя другими зарядами равен
В соответствии с формулой (3) энергия взаимодействия зарядов равна
Такую работу совершит электрическое поле, при удалении всех зарядов на бесконечное расстояние друг от друга.
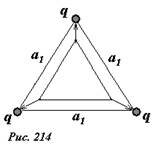
При таком смещении работа электрического поля будет равна уменьшению энергии системы
Обратите внимание, при \(
a_1 \to \infty\) эта работа становится в точности равной начальной энергии U0.
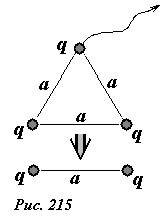
Если из первоначальной системы мы удалим один заряд при неподвижных оставшихся (рис. 215), то энергия системы станет равной
При этом поле совершит работу
Задание для самостоятельной работы.
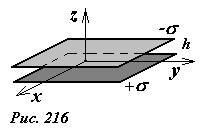
Энергия взаимодействия двух равномерно заряженных параллельных пластин.
Напряженность поля между пластинами была вычислена нами ранее, она равна
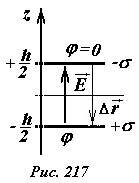
Для «упрощения» расчетов положим потенциал отрицательно заряженной пластины равным нулю, тогда потенциал другой пластины будет равен
Теперь необходимо найти потенциал поля φ’, создаваемого только одной пластиной. Напряженность поля E’, создаваемого одной пластиной в два раза меньше напряженности поля между пластинами \(
Не смотря на то, что противоположно заряженные пластины притягиваются, их энергия оказалась положительной – в этом нет ничего удивительного: мы положили потенциал одной из пластин равным нулю. Это значит, что нулевой энергии соответствует положение, когда положительно заряженная пластина совпадает с отрицательно заряженной, то есть когда пластины совпадают, а электрическое поле отсутствует. Если пластины находятся на некотором расстоянии h друг от друга, то при их сближении поле совершит положительную работу. Наоборот, чтобы разнести пластины, внешние силы должны совершить работу, увеличивая энергию системы.
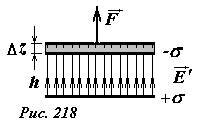
Энергию рассматриваемой системы можно найти, рассчитывая работу внешних сил, по разнесению пластин. На одну из пластин со стороны другой действует сила электрического притяжения \(
Таким образом, мы получаем ту же формулу для энергии систему зарядов. Используя соотношение между напряженностью поля между пластинами и поверхностной плотностью заряда σ = ε0E, выразим энергию взаимодействия через напряженность поля
Как обычно, в неоднородном поле корректное определение плотности энергии «в данной точке» требует предельного перехода: плотностью энергии электрического поля называется отношение энергии поля, заключенной в малом объеме к величине этого объема, при стремлении последнего к нулю
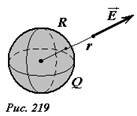
Энергия поля равномерно заряженной сферы.
Пусть электрический заряд Q равномерно распределен по поверхности сферы радиуса R. Вне сферы электрическое поле, создаваемое зарядами на сфере, эквивалентно полю точечного заряда, помещенного в центре сфере (рис. 219). Внутри сферы поле отсутствует. Так напряженность поля в точке, находящейся на расстоянии r от центра сферы равна
в частности непосредственно у поверхности сферы напряженность поля равна
Обратим внимание, что произведение \(
S = 4 \pi R^2\) есть площадь сферы, поэтому отношение \(
\frac <4 \pi \varepsilon_0>= \sigma\) является поверхностной плотностью заряда на сфере, поэтому напряженность поля у поверхности сферы выражается той же формулой, что и напряженность поля между пластинами, рассмотренными в предыдущем разделе \(
E_0 = \frac<\sigma><\varepsilon_0>\). Потенциал поверхности сферы также был вычислен нами ранее
Рассчитаем теперь энергию поля, создаваемого зарядами на сфере. Мысленно разделим заряд сферы на N равных малых частей (рис.220), величины которых равны \(
\delta Q_k = \frac
\varphi_k = \frac<(N-1) \delta Q><4 \pi \varepsilon_0 R>\). С использованием симметричной формулы \(
данная сумма содержит N одинаковых слагаемых, поэтому равна
Так как число частей N, на которые разбивается сфера, может быть сделано сколь угодно большим, поэтому в пределе \(
N \to \infty\) слагаемое \(
\frac<1>
Заметим, что полученное выражение имеет вид \(
U = \frac<1> <2>Q \varphi_0\). Если сразу заявить, что уменьшение заряда на малую величину \(
\delta Q\) пренебрежимо мало изменяет потенциал сферы, то результат (4) получается прямым применением формулы для энергии взаимодействия зарядов. Однако обращение с малыми величинами требует известной строгости, поэтому мы и привели несколько «удлиненный» вывод.
Приведем еще один вывод этой же формулы. Для этого энергию системы рассчитаем как работу, которую необходимо совершить, чтобы зарядить сферу. Мысленно будем заряжать сферу малыми равными порциями заряда \(
\delta Q_k = \frac
Заметьте, что для перенесения каждой следующей порции заряда надо совершать большую работу.
Полная работа по зарядке сферы (равная энергии электрического поля сферы) выражается суммой геометрической прогрессии
Как и следовало ожидать, мы получили выражение, полностью совпадающее с (13), при бесконечном уменьшении порций переносимых зарядов (\(
N \to \infty\)) мы опять приходим к формуле (14).
В этом нет ничего удивительного, так как в первом случае мы подсчитали энергию, которая выделится при разбегании зарядов со сферы, а во втором – энергию, которую необходимо затратить, чтобы собрать их обратно.
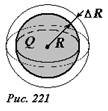
Покажем, что энергию взаимодействия зарядов и в этом случае можно истолковать как энергию электрического поля, «размазанную» по всему пространству, где существует поле. Представим, что радиус сферы увеличился на малую величину ΔR, а ее заряд при этом не изменился. Согласно формуле (14) энергия взаимодействия зарядов при этом уменьшится. В пространстве вне сферы увеличенного радиуса электрическое поле не изменилось, а в тонком сферическом слое между начальной и расширенной сферами – исчезло (рис. 221). Поэтому следует считать, что уменьшение энергии взаимодействия зарядов при увеличении радиуса сферы равно энергии, которая заключена в этом тонком сферическом слое. При малой толщине слоя его объем можно вычислить как произведение площади сферы на толщину слоя \(
На последнем шаге, мы пренебрегли малым изменением радиуса ΔR. Наконец, выразим заряд шара через напряженность электрического поля у его поверхности \(
Q = 4 \pi \varepsilon_0 R^2 E\) :
Из сравнения с формулой (16) следует, что и в рассматриваемом случае плотность энергии электрического поля выражается формулой \(
Плотность энергии это количество энергия хранится в данной системе или области пространства на единицу объем. Его также можно использовать для получения энергии на единицу масса, хотя точный термин для этого удельная энергия (или гравиметрическая плотность энергии). Часто только полезный или извлекаемая энергия измеряется, то есть недоступная энергия (такая как масса покоя энергия) игнорируется. [1] В космологический и другие общерелятивистский контекстах, однако, рассматриваемые плотности энергии соответствуют элементам тензор энергии-импульса и поэтому включают в себя энергию массы, а также плотности энергии, связанные с давлениями, описанными в следующем абзаце.
Содержание
Введение в плотность энергии
В материалах хранятся разные типы энергии, и для высвобождения каждого типа энергии требуется определенный тип реакции. В порядке типичной величины выделяемой энергии эти типы реакций бывают: ядерные, химические, электрохимические и электрические.
Ядерные реакции происходят в звездах и на атомных электростанциях, оба из которых получают энергию из энергии связи ядер. Химические реакции используются животными для получения энергии из пищи и автомобилями для получения энергии из бензина. Жидкие углеводороды (такие виды топлива, как бензин, дизельное топливо и керосин) на сегодняшний день являются наиболее плотным из известных способов экономичного хранения и транспортировки химической энергии в очень больших масштабах (1 кг дизельного топлива горит с кислородом, содержащимся в
15 кг воздуха). Электрохимические реакции используются большинством мобильных устройств, таких как портативные компьютеры и мобильные телефоны, для высвобождения энергии из батарей.
Типы энергоемкости
Есть два вида теплоты сгорания:
Удобную таблицу HHV и LHV некоторых видов топлива можно найти в справочниках. [2]
Плотность энергии в накопителе энергии и в топливе
Широкие последствия
Плотность энергии отличается от эффективность преобразования энергии (чистый выпуск на ввод) или внутренная энергия (затраты энергии на обеспечение, как сбор урожая, очистка, распространение и работа с загрязнение все используют энергию). Широкомасштабное и интенсивное энергопотребление влияет и подвержено влиянию климат, хранилище отходов, и экологические последствия.
Ни один из методов хранения энергии не может похвастаться удельная мощность, удельная энергия, и плотность энергии. Закон Пейкерта описывает, как количество полезной энергии, которое может быть получено (для свинцово-кислотного элемента), зависит от того, как быстро он извлекается. Чтобы максимизировать удельную энергию и плотность энергии, можно вычислить удельная плотность энергии вещества путем умножения двух значений вместе, где чем выше число, тем лучше вещество в плане эффективного хранения энергии.
Обсуждаются альтернативные варианты хранения энергии для увеличения плотности энергии и уменьшения времени зарядки. [10] [11] [12] [13]
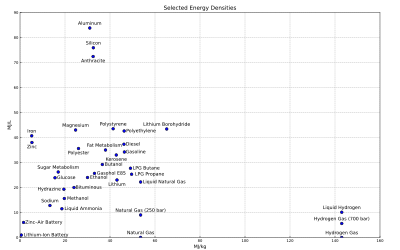
Гравиметрический и объемный удельная энергия некоторых видов топлива и технологий хранения (изменено с Бензин статья):
Таблицы содержания энергии
Если не указано иное, значения в следующей таблице являются более низкая теплотворная способность для идеальное сгорание без учета массы или объема окислителя. При рассмотрении данных в таблице могут быть полезны следующие преобразования единиц измерения: 3,6MJ = 1 кВт⋅ч ≈ 1.34 hp⋅h.
| Тип хранилища | Удельная энергия (МДж / кг) | Плотность энергии (МДж / л) | Удельная энергия (Вт⋅ч / кг) | Плотность энергии (Вт⋅ч / л) | Как высвобождается энергия и комментарии | ||
|---|---|---|---|---|---|---|---|
| Антивещество | 89,875,517,874 = 90 ПДж / кг | Зависит от плотности формы антивещества | 24,965,421,631,578 = 3600 фунтов на кв. Дюйм) | 53.6 [21] | 9 | 14,888.9 | 2,500.0 |
| Натуральный газ | 53.6 [21] | 0.0364 | 14,888.9 | 10.1 | |||
| СУГ пропан [22] | 49.6 | 25.3 | 13,777.8 | 7,027.8 | |||
| СУГ бутан [22] | 49.1 | 27.7 | 13,638.9 | 7,694.5 | |||
| Бензин (бензин) [22] | 46.4 | 34.2 | 12,888.9 | 9,500.0 | Сгорел внутри двигателей внутреннего сгорания. Тепловой КПД от 20 до 40%. | ||
| Полипропилен пластик | 46.4 [23] | 41.7 | 12,888.9 | 11,583.3 | |||
| Полиэтилен пластик | 46.3 [23] | 42.6 | 12,861.1 | 11,833.3 | |||
| Жилой топочный мазут [22] | 46.2 | 37.3 | 12,833.3 | 10,361.1 | |||
| Дизельное топливо [22] | 45.6 | 38.6 | 12,666.7 | 10,722.2 | Сгорел внутри двигателей внутреннего сгорания. Тепловой КПД от 25 до 40%. | ||
| 100LL Avgas | 44.0 [24] | 31.59 | 12,222.2 | 8,775.0 | |||
| Реактивное топливо (например. Керосин) | 43 [25] [26] [27] | 35 | Авиационный двигатель | ||||
| Газохол E10 (10% этанола 90% бензина по объему) | 43.54 | 33.18 | 12,094.5 | 9,216.7 | |||
| Литий | 43.1 | 23.0 | 11,972.2 | 6,388.9 | |||
| Биодизель масло (растительное масло) | 42.20 | 33 | 11,722.2 | 9,166.7 | |||
| DMF (2,5-диметилфуран) [ требуется разъяснение ] | 42 [28] | 37.8 | 11,666.7 | 10,500.0 | |||
| Сырая нефть (согласно определению тонна нефтяного эквивалента) | 41.868 | 37 [21] | 11,630 | 10,278 | |||
| Полистирол пластик | 41.4 [23] | 43.5 | 11,500.0 | 12,083.3 | |||
| Телесный жир | 38 | 35 | 10,555.6 | 9,722.2 | Обмен веществ в организме человека (КПД 22% [29] ) | ||
| Бутанол | 36.6 | 29.2 | 10,166.7 | 8,111.1 | |||
| Газохол E85 (85% этанол 15% бензина по объему) | 33.1 | 25.65 [ нужна цитата ] | 9,194.5 | 7,125.0 | |||
| Графитовый | 32.7 | 72.9 | 9,083.3 | 20,250.0 | |||
| Уголь, антрацит [6] | 26–33 | 34–43 | 7,222.2–9,166.7 | 9,444.5–11,944.5 | Цифры представляют идеальное сгорание без учета окислителя, но КПД преобразования в электричество составляет 36%. | ||
| Кремний [30] | 1.790 | 4.5 | 500 | 1,285 | Энергия, накопленная за счет перехода кремния из твердой фазы в жидкую | ||
| Алюминий | 31.0 | 83.8 | 8,611.1 | 23,277.8 | |||
| Этиловый спирт | 30 | 24 | 8,333.3 | 6,666.7 | |||
| DME [31] [32] | 31,7 (HHV) 28,4 (л / с) | 21,24 (HHV) 19.03 (LHV) | 8,805.6 8805,6 (HHV) 7 888,9 (LHV) | 5900,0 (HHV) 5 286,1 (LHV) | |||
| Полиэстер пластик | 26.0 [23] | 35.6 | 7,222.2 | 9,888.9 | |||
| Магний | 24.7 | 43.0 | 6,861.1 | 11,944.5 | |||
| Уголь, битумный [6] | 24–35 | 26–49 | 6,666.7–9,722.2 | 7,222.2–13,611.1 | |||
| ПЭТ пластик (нечистый) | 23.5 [33] | 6,527.8 | |||||
| Метанол | 19.7 | 15.6 | 5,472.2 | 4,333.3 | |||
| Гидразин (сгорел до N2+ H2O) | 19.5 | 19.3 | 5,416.7 | 5,361.1 | |||
| Жидкость аммиак (сгорел до N2+ H2O) | 18.6 | 11.5 | 5,166.7 | 3,194.5 | |||
| ПВХ пластик (неправильное горение токсично) [ требуется разъяснение ] | 18.0 [23] | 25.2 | 5,000.0 | 7,000.0 | |||
| Дерево [34] | 18.0 | 5,000.0 | |||||
| Торф брикет [35] | 17.7 | 4,916.7 | |||||
| Сахар, углеводы и белок [ нужна цитата ] | 17 | 26.2 (декстроза) | 4,722.2 | 7,277.8 | Обмен веществ в организме человека (КПД 22% [36] ) | ||
| Кальций [ нужна цитата ] | 15.9 | 24.6 | 4,416.7 | 6,833.3 | |||
| Глюкоза | 15.55 | 23.9 | 4,319.5 | 6,638.9 | |||
| Сухой коровий навоз и верблюжий навоз | 15.5 [37] | 4,305.6 | |||||
| Уголь, лигнит [ нужна цитата ] | 10–20 | 2,777.8–5,555.6 | |||||
| Натрий | 13.3 | 12.8 | 3,694.5 | 3,555.6 | сгорел до мокрого гидроксид натрия | ||
| Торф | 12.8 | 3,555.6 | |||||
| Нитрометан | 11.3 | 3,138.9 | |||||
| Сера | 9.23 | 19.11 | 2,563.9 | 5,308.3 | сгорел до диоксид серы [38] | ||
| Натрий | 9.1 | 8.8 | 2,527.8 | 2,444.5 | сгорел, чтобы высохнуть оксид натрия | ||
| Батарея воздушно-литиевая перезаряжаемая | 9.0 [39] | 2,500.0 | Контролируемый электрический разряд | ||||
| Бытовые отходы | 8.0 [40] | 2,222.2 | |||||
| Цинк | 5.3 | 38.0 | 1,472.2 | 10,555.6 | |||
| Утюг | 5.2 | 40.68 | 1,444.5 | 11,300.0 | сгорел до оксид железа (III) | ||
| Тефлон пластик | 5.1 | 11.2 | 1,416.7 | 3,111.1 | горючий токсичный, но негорючий | ||
| Утюг | 4.9 | 38.2 | 1,361.1 | 10,611.1 | сгорел до оксид железа (II) | ||
| Порох | 4.7–11.3 [41] | 5.9–12.9 | |||||
| TNT | 4.184 | 6.92 | |||||
| ANFO | 3.7 | 1,027.8 | |||||
| Батарея воздушно-цинковая [42] | 1.59 | 6.02 | 441.7 | 1,672.2 | Контролируемый электрический разряд | ||
| Жидкий азот | 0.77 [43] | 0.62 | 213.9 | 172.2 | Максимальная обратимая работа при 77,4 К с резервуаром 300 К | ||
| Натрий-серная батарея | 0.54–0.86 | 150–240 | |||||
| Сжатый воздух при 300 бар | 0.5 | 0.2 | 138.9 | 55.6 | Потенциальная энергия | ||
| Скрытая теплота плавления льда [ нужна цитата ] (термический) | 0.335 | 0.335 | 93.1 | 93.1 | |||
| Литий-металлический аккумулятор | 1.8 | 4.32 | Контролируемый электрический разряд | ||||
| Литий-ионный аккумулятор | 0.36–0.875 [46] | 0.9–2.63 | 100.00–243.06 | 250.00–730.56 | Контролируемый электрический разряд | ||
| Маховик | 0.36–0.5 | 5.3 | Потенциальная энергия | ||||
| Щелочная батарея | 0.48 [47] | 1.3 [48] | Контролируемый электрический разряд | ||||
| Никель-металлогидридная батарея | 0.41 [49] | 0.504–1.46 [49] | Контролируемый электрический разряд | ||||
| Свинцово-кислотная батарея | 0.17 | 0.56 | Контролируемый электрический разряд | ||||
| Суперконденсатор (EDLC) | 0.01–0.030 [50] [51] [52] [53] [54] [55] [56] | 0.006–0.06 [50] [51] [52] [53] [54] [55] | до 8,57 [56] | Контролируемый электрический разряд | |||
| Вода на высоте 100 м плотины | 0.000981 | 0.000978 | 0.272 | 0.272 | Цифры представляют потенциальную энергию, но эффективность преобразования в электричество составляет 85–90%. [57] [58] | ||
| Электролитический конденсатор | 0.00001–0.0002 [59] | 0.00001–0.001 [59] [60] [61] | Контролируемый электрический разряд | ||||
| Тип хранилища | Плотность энергии по массе (МДж / кг) | Плотность энергии по объему (МДж / л) | Удельная энергия (Вт⋅ч / кг) | Плотность энергии (Вт⋅ч / л) | Как высвобождается энергия и комментарии |
Емкость хранения механической энергии, или стойкость, из Hookean Материал, когда он деформирован до точки разрушения, можно рассчитать, вычислив предел прочности на разрыв, умноженный на максимальное относительное удлинение, деленное на два. Максимальное удлинение материала Гука можно вычислить, разделив жесткость этого материала на его предел прочности при растяжении. В следующей таблице перечислены эти значения, вычисленные с использованием модуля Юнга в качестве меры жесткости:
| Материал | Плотность энергии по массе | Устойчивость: Плотность энергии по объему | Предел прочности при растяжении прочность | ||
|---|---|---|---|---|---|
| Резинка | 1,651–6,605 [62] | 2,200–8,900 [62] | 1.35 [62] | ||
| Сталь, ASTM A228 (выход, диаметр 1 мм) | 1,440–1,770 | 11,200–13,800 | 7.80 [63] | 210 [63] | 2,170–2,410 [63] |
| Ацетали | 908 | 754 | 0.831 [64] | 2.8 [65] | 65 (максимальная) [65] |
| Нейлон-6 | 233–1,870 | 253–2,030 | 1.084 | 2–4 [65] | 45–90 (максимальная) [65] |
| Медь Бериллий 25-1 / 2 HT (доходность) | 684 | 5,720 [66] | 8.36 [67] | 131 [66] | 1,224 [66] |
| Поликарбонаты | 433–615 | 520–740 | 1.2 [68] | 2.6 [65] | 52–62 (максимальная) [65] |
| АБС-пластик | 241–534 | 258–571 | 1.07 | 1.4–3.1 [65] | 40 (максимум) [65] |
| Акрил | 1,530 | 3.2 [65] | 70 (максимум) [65] | ||
| Алюминий 7077-Т8 (Уступать) | 399 | 1120 [66] | 2.81 [69] | 71.0 [66] | 400 [66] |
| Сталь, нержавеющий, 301-Н (выход) | 301 | 2,410 [66] | 8.0 [70] | 193 [66] | 965 [66] |
| Эпоксидные смолы | 113–1810 | 2–3 [65] | 26–85 (максимальная) [65] | ||
| Пихта Дугласа Вуд | 158–200 | 96 | .481–.609 [71] | 13 [65] | 50 (сжатие) [65] |
| Сталь, мягкая AISI 1018 | 42.4 | 334 | 7.87 [72] | 205 [72] | 370 (440 Максимальное) [72] |
| Алюминий (нелегированный) | 32.5 | 87.7 | 2.70 [73] | 69 [65] | 110 (максимальная) [65] |
| Сосна (Американская восточная белая, изгиб) | 31.8–32.8 | 11.1–11.5 | .350 [74] | 8.30–8.56 (изгиб) [74] | 41,4 (изгиб) [74] |
| Латунь | 28.6–36.5 | 250–306 | 8.4–8.73 [75] | 102–125 [65] | 250 (максимальная) [65] |
| Медь | 23.1 | 207 | 8.93 [75] | 117 [65] | 220 (максимальная) [65] |
| Стекло | 5.56–10.0 | 13.9–25.0 | 2.5 [76] | 50–90 [65] | 50 (сжатие) [65] |
Таблица энергоемкости батарей:
| Устройство хранения | Содержание энергии (Джоуль) | Тип энергии | Типичный масса (г) | Типовые размеры (диаметр × высота в мм) | Типичный объем (мл) | Плотность энергии по объему (МДж / л) | Плотность энергии по массе (МДж / кг) |
|---|---|---|---|---|---|---|---|
| Щелочной Батарея AA [77] | 9,360 | Электрохимический | 24 | 14.2 × 50 | 7.92 | 1.18 | 0.39 |
| Щелочной C аккумулятор [77] | 34,416 | Электрохимический | 65 | 26 × 46 | 24.42 | 1.41 | 0.53 |
| NiMH Батарея AA | 9,072 | Электрохимический | 26 | 14.2 × 50 | 7.92 | 1.15 | 0.35 |
| NiMH C аккумулятор | 19,440 | Электрохимический | 82 | 26 × 46 | 24.42 | 0.80 | 0.24 |
| Литий-ионный 18650 аккумулятор | 28,800–46,800 | Электрохимический | 44–49 [78] | 18 × 65 | 16.54 | 1.74–2.83 | 0.59–1.06 |
Источники ядерной энергии
Источниками энергии самой высокой плотности помимо антивещества являются: слияние и деление. Fusion включает в себя энергию солнца, которая будет доступна в течение миллиардов лет (в форме солнечного света), но пока (2018 г.) термоядерная энергия производство по-прежнему неуловимо.
Мощность от деления урана и тория в атомная энергия растения будут доступны в течение многих десятилетий или даже столетий из-за обилия элементов на земле, [79] хотя весь потенциал этого источника можно реализовать только через реакторы-размножители, которые, помимо Реактор БН-600, пока не используется в коммерческих целях. [80] Уголь, газ, и нефть являются текущими первичными источниками энергии в США. [81] но имеют гораздо меньшую плотность энергии. Горящий местный биомасса топливо обеспечивает бытовые потребности в энергии (приготовление огня, масляные лампыи др.) по всему миру.
Тепловая мощность ядерных реакторов деления
Плотность тепловой энергии, содержащейся в ядре легководный реактор (PWR или BWR) обычно 1 ГВт (электрическая мощность 1000 МВт соответствует
3000 МВт тепловой) находится в диапазоне от 10 до 100 МВт тепловой энергии на кубический метр охлаждающей воды в зависимости от рассматриваемого местоположения в системе (сама активная зона (
30 м 3 ), корпус реактора (
50 м 3 ) или весь первый контур (
300 м 3 )). Это представляет собой значительную плотность энергии, которая требует при любых обстоятельствах непрерывного потока воды с высокой скоростью, чтобы можно было удалить высокая температура от активной зоны даже после аварийной остановки реактора. Неспособность остудить три ядра реакторы с кипящей водой (BWR) на Фукусима в 2011 году после цунами и результирующая потеря внешней электроэнергии и холодного источника стала причиной расплавления трех сердечников всего за несколько часов, хотя три реактора были правильно остановлены сразу после Землетрясение Тохоку. Эта чрезвычайно высокая удельная мощность отличает атомные электростанции (АЭС) от любых тепловых электростанций (сжигающих уголь, топливо или газ) или любых химических предприятий и объясняет большую избыточность, необходимую для постоянного контроля нейтронная реактивность и для отвода остаточного тепла от активной зоны АЭС.
Плотность энергии электрического и магнитного полей
Электрический и магнитные поля хранить энергию. В вакууме (объемная) плотность энергии определяется выражением
ты = ε 0 2 E 2 + 1 2 μ 0 B 2 < displaystyle u = < frac < varepsilon _ <0>> <2>> mathbf
где E это электрическое поле и B это магнитное поле. Решение будет (в единицах СИ) в Джоулях на кубический метр. В контексте магнитогидродинамика, физика проводящих жидкостей, плотность магнитной энергии ведет себя как дополнительная давление что добавляет к давление газа из плазма.
В нормальных (линейных и недисперсных) веществах плотность энергии (в единицах СИ) равна
В случае отсутствия магнитных полей, используя Отношения Фрёлиха эти уравнения также можно распространить на анизотропный и нелинейный диэлектриков, а также для расчета коррелированных Свободная энергия Гельмгольца и энтропия плотности. [82]
Когда пульсирует лазер ударяется о поверхность, лучистая экспозиция, т.е. энергия, выделяемая на единицу поверхности, может быть названа плотность энергии или флюенс. [83]