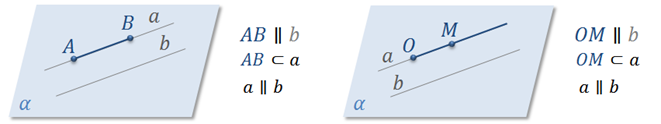что такое параллельные прямые в пространстве
Параллельные прямые в пространстве
Урок 4. Геометрия 10 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Параллельные прямые в пространстве»
· рассмотрим понятие параллельных прямых в пространстве;
· дадим определение параллельных прямых в пространстве;
· докажем теорему единственности прямой, параллельной данной.
Ранее в планиметрии мы с вами уже рассматривали взаимное расположение двух прямых на плоскости. Напомню, что возможны три случая:
Первый случай. Прямые параллельны, т.е. две прямые не имеют общих точек.
Второй случай. Прямые пересекаются, т.е. две прямые имеют одну общую точку.
И третий случай. Прямые совпадают, т.е. имеют более чем одну общую точку.
Теперь перейдем к стереометрии. Напомню, что стереометрия изучает свойства фигур в пространстве.
Рассмотрим прямоугольный параллелепипед ABCDA1B1C1D1. Как вы уже знаете, параллелепипед – это пространственное тело.
Прямые, на которых лежат его ребра, например, A1B1, D1C1 и DC – параллельны. Прямые, через которые проходят диагонали его грани, например, D1C1 и DC – пересекаются. А вот прямые, на которых лежат диагональ параллелепипеда A1C и ребро B1C1 называются скрещивающимися.
Сделаем вывод: две прямые в пространстве могут пересекаться, быть параллельными или скрещиваться.
Пересекающиеся и параллельные прямые задают некоторую плоскость. Скрещивающиеся прямые – это прямые, через которые нельзя провести плоскость.
Давайте подробно остановимся на случае с параллельными прямыми в пространстве.
Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Обратите внимание, что оговорка «если они лежат в одной плоскости» в определении очень важна. Так как в стереометрии мы с вами рассматриваем трехмерное пространство и, если две прямые лежат в разных плоскостях, то нельзя говорить про их параллельность. Параллельными прямые могут быть только если лежат в одной плоскости.
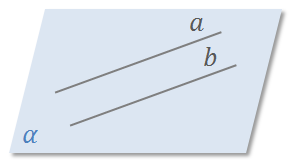
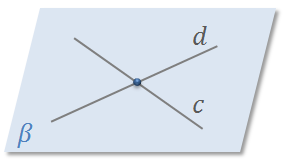
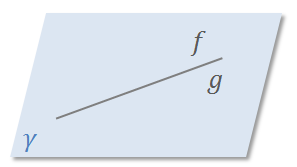
Если прямые а и b параллельны, то это обозначают следующим образом 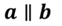
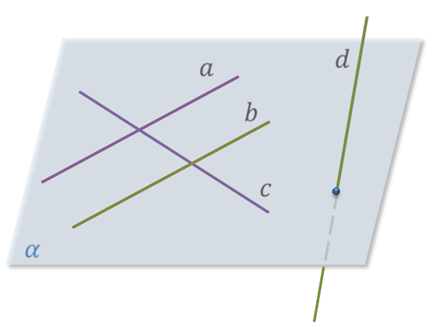
Посмотрим внимательно на рисунок.
Здесь прямые а и b параллельны. А вот прямые а и c, b и d– не параллельны.
Приведем несколько примеров параллельных прямых в пространстве. Знакомые каждому железнодорожные рельсы.
На ровной местности их можно рассматривать, как параллельные прямые.
А посмотрите внимательно на свою тетрадь. Обратите внимание, противоположные края тетрадного листа также лежат на параллельных прямых.
Прямые, по которым плоскость стены комнаты пересекает плоскости потолка и пола. Они также являются параллельными.
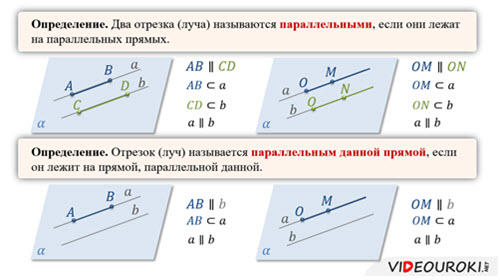
Запишем определения. Два отрезка (луча) называются параллельными, если они лежат на параллельных прямых.
Отрезок (луч) называется параллельным данной прямой, если он лежит на прямой, параллельной данной.
Справедлива теорема о параллельности прямых. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.
Докажем эту теорему.
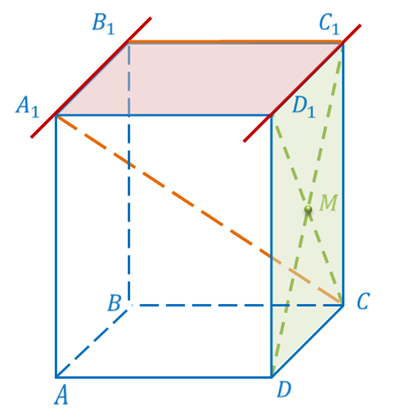
Рассмотрим прямую а и точку М, не лежащую на этой прямой. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна. Тогда через нашу прямую а и точку М проходит единственная плоскость. Давайте обозначим эту плоскость буквой α. Прямая, проходящая через точку М параллельно прямой а, должна лежать в одной плоскости с точкой М и прямой а. Т.е. должна лежать в плоскости α. Из курса планиметрии вы помните, что через каждую точку плоскости, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной прямой. Следовательно, в плоскости α через точку М проходит прямая, параллельная прямой а, и притом только одна. На рисунке эта прямая обозначена буквой b.
Докажем единственность прямой b. Предположим, что существует еще одна прямая, например, b1, которая проходит через точку М и параллельна прямой а. Тогда эта прямая b1 должна лежать в одной плоскости с точкой М и прямой а. Т.е. в плоскости α. А из курса планиметрии вы знаете, что в плоскости α через точку М проходит единственная прямая, параллельная прямой а. Значит, прямая b1 совпадает с прямой b.
Таким образом, прямая b – это единственная прямая, проходящая через точку М параллельно прямой а. Теорема доказана.
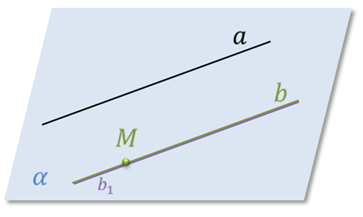
Замечание. Если прямые в пространстве параллельны, то на чертеже они обязательно изображаются параллельными прямыми.
А вот если прямые на чертеже изображены параллельными прямыми, то в пространстве эти прямые не обязательно параллельны.
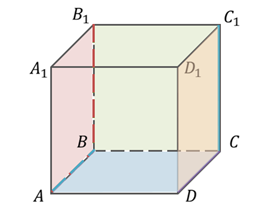
Задание. Дан куб 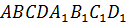
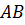
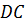
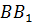
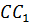
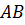
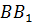
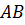
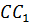
Решение. Рассмотрим куб ABCDA1B1C1D1. Напомню, что куб – это прямоугольный параллелепипед, все грани которого – равные квадраты.
Рассмотрим прямые AB и DC. Они лежат в одной плоскости ABC и не пересекаются. Следовательно, прямые AB и DC параллельны.
Аналогично и прямые BB1 и CC1. Они лежат в одной плоскости BB1C1 и не пересекаются. Следовательно, параллельны.
Теперь рассмотрим прямые AB и BB1. Хоть они и лежат в одной плоскости ABB1, но пересекаются в точке B. Значит, прямые AB и BB1 не параллельны.
Осталось рассмотреть прямые AB и CC1. Они не пересекаются, но и не лежат в одной плоскости. Значит, они не параллельны.
Ответ: а) 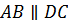
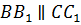
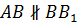
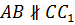
Подведем итоги урока. На этом уроке мы рассмотрели понятие параллельных прямых в пространстве. Узнали, что две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются. А также доказали теорему о том, что через любую точку пространства можно провести только одну прямую, параллельную данной.
Параллельность прямых
Определение параллельности прямых
Начнем с главного — определимся, какие прямые параллельны согласно евклидовой геометрии. Мы недаром упомянули Евклида, ведь именно в его трудах, написанных за 300 лет до н. э., до нас дошли первые упоминания о параллельности.
Параллельными называются прямые в одной плоскости, не имеющие точек пересечения, даже если их продолжать бесконечно долго. Обозначаются они следующим образом: a II b.
Казалось бы, здесь все просто, но со времен Евклида над определением параллельных прямых и признаками параллельности прямых бились лучшие умы. Особый интерес вызывал 5-й постулат древнегреческого математика: через точку, которая не относится к прямой, в той же плоскости можно провести только одну прямую, параллельную первой. В XIX веке российский математик Н. Лобачевский смог опровергнуть постулат и указать на условия, при которых возможно провести как минимум 2 параллельные прямые через одну точку.
Впрочем, поскольку школьная программа ограничена евклидовой геометрией, вышеуказанное утверждение мы принимаем как аксиому.
На плоскости через любую точку, не принадлежащую некой прямой, можно провести единственную прямую, которая была бы ей параллельна.
Свойства и признаки параллельных прямых
Есть ряд признаков, по которым можно определить, что одна прямая параллельна другой. К счастью, свойства и признаки параллельности прямых тесно связаны, поэтому не придется запоминать много информации.
Начнем со свойств. Для этого проведем третью прямую, пересекающую параллельные прямые — она будет называться секущей. В результате у нас образуется 8 углов.
Если секущая проходит через две параллельные прямые, то:
∠4 + ∠6 = 180°; ∠3 + ∠5 = 180°.
∠1 = ∠5, ∠3 = ∠7, ∠4 = ∠8, ∠2 = ∠6.
Вышеуказанные свойства являются одновременно признаками, по которым мы можем сделать вывод о параллельности прямых. Причем достаточно установить и доказать лишь один признак — остальные будут к нему прилагаться.
А сейчас посмотрим, как все это помогает решать задачи и практиковаться в определении параллельности двух прямых.
Задача 1
Прямые MN и KP пересекают две другие прямые, образуя несколько углов. Известно, что ∠1 = 73°; ∠3 = 92°; ∠2 = 73°. Требуется найти величину ∠4.
Решение
Поскольку ∠1 и ∠2 являются соответственными, их равенство говорит о том, что MN II KP. Следовательно, ∠3 = ∠MPK = 92°.
Согласно другому свойству параллельных прямых ∠4 + ∠MPK = 180°.
Задача 2
Две параллельные прямые а и b удалены друг от друга на расстояние 27 см. Секущая к этим прямым образует с одной из них угол в 150°. Требуется найти величину отрезка секущей, расположенного между а и b.
Решение
Поскольку а II b, значит ∠MKD + ∠KDN = 180°.
Теперь рассмотрим треугольник KDM. Мы знаем, что отрезок DM представляет собой расстояние между прямыми а и b, а значит, DM ┴ b и наш треугольник является прямоугольным.
Поскольку катет, противолежащий углу в 30°, равен ½ гипотенузы, DM = 1/2DK.
Видеоурок «Параллельные прямые в пространстве»
Ранее в планиметрии мы с вами уже рассматривали взаимное расположение двух прямых на плоскости. Напомним, что возможны три случая.
Первый случай. Прямые параллельны, то есть две прямые не имеют общих точек.
Второй случай. Прямые пересекаются, то есть две прямые имеют одну общую точку.
И третий случай. Прямые совпадают, то есть имеют более чем одну общую точку.
Теперь перейдём к стереометрии. Напомним, что стереометрия изучает свойства фигур в пространстве.
Рассмотрим прямоугольный параллелепипед 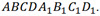
Прямые, на которых лежат его ребра, например 
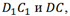
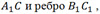
Сделаем вывод: две прямые в пространстве могут пересекаться, быть параллельными или скрещиваться.
Пересекающиеся и параллельные прямые задают некоторую плоскость. Скрещивающиеся прямые — это прямые, через которые нельзя провести плоскость.
Давайте подробно остановимся на случае с параллельными прямыми в пространстве.
Запишем определение параллельных прямых в пространстве.
Обратите внимание, что оговорка «если они лежат в одной плоскости» в определении очень важна. Так как в стереометрии мы с вами рассматриваем трёхмерное пространство и, если две прямые лежат в разных плоскостях, нельзя говорить про их параллельность. Параллельными прямые могут быть, только если лежат в одной плоскости.
Приведём несколько примеров параллельных прямых в пространстве.
Запишем определения параллельных отрезков и параллельных лучей в пространстве.
Справедлива теорема о параллельности прямых. Сформулируем и докажем её.
Замечание. Если прямые в пространстве параллельны, то на чертеже они обязательно изображаются параллельными прямыми. А вот если прямые на чертеже изображены параллельными прямыми, то в пространстве эти прямые не обязательно параллельны.
Геометрия. 10 класс
Конспект урока
Геометрия, 10 класс
Урок №4. Параллельность прямых, прямой и плоскости
Перечень вопросов, рассматриваемых в теме
Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Определение. Скрещивающиеся прямые − прямые, которые не лежат в одной плоскости.
Определение. Два отрезка называются параллельными, если они лежат на паралельных прямых.
Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия 10-11 кл.– М.: Просвещение, 2014. 255 с.
Зив Б. Г. Дидактические материалы. Геометрия 10 кл. – М.: Просвещение, 2014. 96 с.
Глазков Ю. А., Юдина И. И., Бутузов В.Ф. Рабочая тетрадь. Геометрия 10 кл.-М.: Просвещение, 2013. 65 с.
Теоретический материал для самостоятельного изучения
Геометрия, которую мы изучаем, называется евклидовой, по имени древнегреческого ученого Евклида (3 век до нашей эры), который создал целый труд по математике под названием «Начала». В данной книге есть раздел о параллельных прямых.
В советском энциклопедическом словаре слово «параллельность» переводится с греческого языка, как «идущий рядом».
В средние века параллельность обозначалась знаком «=». В 1557 году Р. Рекордом для обозначения равенства был введен знак «=», которым мы пользуемся сейчас, а параллельность стали обозначать «║».
В книге «Начала» определение параллельных прямых звучало так «прямые, лежащие в одной плоскости и будучи бесконечно продолжены в обе стороны, ни с той, ни с другой стороны не пересекаются». Это определение почти не отличается от современного.
В области параллельных прямых работало очень много учёных: Н.И. Лобаческий (18-19 век); Аббас ал-Джаухари (работал в Багдаде в 9 веке); Фадл ал-Найризи (Богдад 10 век); Герард (Италия 12 век); Иоганн Генрих Ламберт (Берлин) и многие другие.
Каково расположение 2-х прямых на плоскости (совпадают, пересекаются, параллельны) (рис. 1 а, б, в).
Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Определение. Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.

Давайте укажем некоторые пары параллельных прямых:
AB||A₁B₁; AB|| CD; A₁B₁||C₁D₁; CD||C₁D₁; AD||A₁D₁; BC||B₁D₁; AD||BC; A₁D₁||B₁C₁.
А теперь рассмотрим некоторые пары скрещивающихся прямых, как мы отметили, они не должны лежать в одной плоскости:
AB A₁D₁; AB B₁C₁; CD A₁D₁; CD B₁C₁; BC C₁D₁; BC A₁B₁; AB B₁C₁; AB A₁D₁.
Теорема. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.
Определение. Два отрезка называются параллельными, если они лежат на паралельных прямых.
Аналогично определяется праралельность отрезка и прямой, а так же паралельность двух лучей.

Если в этой плоскости одна из параллельных прямых b пересекает прямую p, то вторая прямая a тоже пересекает p.
Так как точка N находится на прямой p, то N находится в плоскости α и является единственной общей точкой прямой a и плоскости α.
Нам известно из курса планиметрии, что если три прямые лежат в одной плоскости и две из них параллельны третьей, то эти две прямые параллельны. Похожее утверждение имеет место и для трех прямых в пространстве.
Теорема. Если две прямые параллельны третьей прямой, то они параллельны.

Выберем точку M на прямой b.
Через точку M и прямую a, которая не содержит эту точку, можно провести только одну плоскость α (Через прямую и не лежащую на ней точку можно провести только одну плоскость).
Возможны два случая:
1) прямая b пересекает плоскость α или 2) прямая b находится в плоскости α.
Пусть прямая b пересекает плоскость α.
Значит, прямая c, которая параллельна прямой b, тоже пересекает плоскость α. Так как a∥c, то получается, что a тоже пересекает эту плоскость. Но прямая a не может одновременно пересекать плоскость α и находиться в плоскости α. Получаем противоречие, следовательно, предположение, что прямая b пересекает плоскость α, является неверным. Значит, прямая b находится в плоскости α.
Теперь нужно доказать, что прямые a и b параллельны.
Пусть у прямых a и b есть общая точка L.
Это означает, что через точку L проведены две прямые a и b, которые параллельны прямой c. Но по второй теореме это невозможно. Поэтому предположение неверное, и прямые a и b не имеют общих точек.
Так как прямые a и b находятся в одной плоскости α и у них нет общих точек, то они параллельны.
Если две точки прямой лежат в данной плоскости, то по аксиоме А₂ вся прямая лежит в этой плоскости. Из этого следует, что возможны три расположения прямой и плоскости:
Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.
Наглядный пример, который дает представление о прямой, параллельной плоскости- это линия пересечения стены и потолка-она параллельна плоскости пола.
Теорема (Признак параллельности прямой и плоскости)
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой на этой плоскости, то эта прямая параллельна данной плоскости.
Доказательство:
Доказательство проведем от противного. Пусть a не параллельна плоскости α, тогда прямая a пересекает плоскость в некоторой точке A. Причем A не находится на b, так как a∥b. Согласно признаку скрещивающихся прямых, прямые a и b скрещивающиеся.
Мы пришли к противоречию. Так как согласно данной информации a∥b, они не могут быть скрещивающимися. Значит, прямая a должна быть параллельна плоскости α.
Существует еще два утверждения, которые используются при решении задач:
Примеры и разбор решения заданий тренировочного модуля
Тип задания: Ввод с клавиатуры пропущенных элементов в тексте
Дано: в ∆ АВС КМ − средняя линия, КМ=5; ACFE- параллелограмм.
Решение: Т.к. КМ − средняя линия, то АС= 2·КМ, то АС=2·7=10
Т.к. ACFE − параллелограмм, то АС=EF=10
Тип задания: Единичный / множественный выбор
Точка М не лежит в плоскости ромба ABCD. На отрезке АМ выбрана точка Е так, что MЕ:ЕА=1:3. Точка F – точка пересечения прямой МВ с плоскостью CDE. Найдите АВ, если AD= 8 cм.
MC
Т.к. AD||BC||FK, следовательно, треугольники MFK и MBC- подобны (по трем углам). Значит