что такое отрицательное математическое ожидание
Что такое отрицательное математическое ожидание
Принято считать, что основной товар в казино — это адреналин. Часто мы слышим, что казино предлагает вытянуть «счастливый билет», много реже говорят что казино продает сервис. На самом же деле, основной товар казино — это азарт от возможности выигрыша. В этой статье мы рассмотрим основные принципы, на которых организована работа игорных домов, обоснование прибыли заведения, и какую роль в ее деятельности играет «госпожа удача».
Математика игр казино
Рассмотрим процессы, происходящие в азартных играх, с точки зрения теории вероятности, и попробуем определить, подчиняются ли игры казино математике.
Бросая монету, можно утверждать, что любая из ее сторон может выпасть с одинаковой вероятностью. Есть всего две возможности — выпадет либо орел, либо решка. Вероятность того, что при бросании монеты выпадет решка равна? (50%), то есть мы вправе ожидать, что в половине случаев будет выпадать решка. Часто говоря о вероятности употребляют слово шанс. Шанс на то, что при броске монеты она упадет решкой вверх, равен 50%
Вероятность показывает, как часто ожидаемый нами результат может быть достигнут, и может быть представлена как отношение ожидаемых исходов к общему количеству всех возможных исходов за достаточно продолжительный период времени при большом количестве повторений.
Математическое ожидание при игре в рулетку

Как вы уже наверное заметили, в обоих приведенных примерах, величина математического ожидания имеет знак «-», что характерно для большинства ставок казино. Отрицательное математическое ожидание на практике означает, что, чем дольше длится игра, тем больше вероятность проигрыша для игрока.
Перевес казино (House Edge) [доля заведения] – величина, противоположная математическому ожиданию игрока и показывающая, какой процент от ставок, сделанных в процессе игры за определенный промежуток времени, удерживается в пользу казино.Сейчас мы будем рассматривать самый популярный вид игры в казино, знаете какой? Самая популярная игра казино во всем мире — это игра в рулетку.Перевес казино в европейской рулетке составляет 1 — 36/37 = 2,7%, в американской рулетке уже 1 — 36/38 = 5,26% (за счет двух зеро). Это означает, что, если вы, играя в рулетку, за определенное время поставили в общей сложности 1000 долларов, то велика вероятность, что в конечном итоге около 27$ (европейская рулетка) и 54$ (американская рулетка) пойдет в доход игорному заведению. В настольных играх перевес казино меньше (Баккара, Блэкджек или Крэпс), поэтому шансы выиграть в них выше.
В качестве примера посчитаем, каковы наши шансы в казино при игре в американскую версию рулетки, игровое колесо которой, напомню, насчитывает 38 секторов (1-36 цифры + 2 сектора зеро). Предположим, что мы поставили на число. Оплата выигрыша, в этом случае производится в соотношении 1 к 36
Выводы:
Не надо быть великим математиком, чтобы играть в казино. Можно даже не считать математическое ожидание и дисперсию — это сделали до вас и можно пользоваться готовыми результатами. Главное понимать, что игры, имеющие большую величину математического ожидания, выгоднее для игрока, так как в них преимущество казино перед вами меньше и, соответственно, время вашей игры и возможная сумма выигрыша увеличивается. Ищите игры, в которых реализовано преимущество игрока, только в этом случае вы можете рассчитывать на выигрыш в достаточно долгой игре.
При выборе рулетки отдавайте предпочтение европейскому варианту (с одним «зеро») так как в ней преимущество казино будет 2,7%, в отличии от американской версии (с двумя «зеро»), в котором перевес игорного заведения равен уже 5,26%.
Но, рассуждая о положительных и отрицательных математических ожиданиях, вы не должны забывать и о том, что существует дисперсия. И чем она выше, тем больше вас будет «лихорадить» в игре. Вы будете проигрывать в играх с преимуществом игрока, и, в то же время, можете выиграть там, где казино имеет значительный перевес математического ожидания. Помните, что вся математика азартных игр казино корректно работает только в случае, когда число попыток велико и, поэтому, достигнуть на практике расчетных ожидаемых величин достаточно сложно из-за ограниченности бюджета игрока, величины ставок или времени игры.
Источник[1];
Отдельная благодарность Алексею Маркову и его книге «Хулиномика».
Именно из за него и его творения побудилась идея создания данной статьи.
Математическое ожидание в трейдинге
Помимо фундаментального и технического анализа в трейдинге большую роль играет математика. Для успешной работы в качестве трейдера вы должны иметь четкую систему управления капиталом, важным параметром которой является такое понятие как математическое ожидание.
Казалось бы, чего тут заморачиваться, если количество прибыльных сделок превышает количество убыточных, то всё, что называется, «на мази» и можно спокойно работать и дальше. Однако не всё так просто, ведь количество не всегда означает качество. И даже в том случае, когда прибыльных сделок по факту получается больше чем убыточных, трейдер всё равно может остаться в минусе. И причиной тому будет ни что иное, как отрицательное математическое ожидание.
Трейдер может в совершенстве знать технический и фундаментальный анализ, но при торговле с отрицательным математическим ожиданием он будет обречен на неудачу. Даже если благодаря использованию, какого либо из указанных выше видов анализа в отдельности или вместе взятых, трейдер совершает 8 прибыльных сделок из 10, он все равно может оказаться в минусе. Если, например, его прибыль по каждой прибыльной сделке составила 10 пунктов, а по каждой убыточной 50 пунктов, то в результате он имеет:
Прибыль: 8х10=80 пунктов;
Убыток: 2х50=100 пунктов;
Итого: 80-100=-20 пунктов убытка.
Математическое ожидание вычисляется по следующей формуле:
Математическое ожидание=вероятность получения прибыли х средняя прибыль от одной сделки – вероятность получения убытков х средний убыток от одной сделки.
Так в приведенном выше примере математическое ожидание отрицательное:
А если бы, например, трейдер заключал прибыльные и убыточные сделки с вероятностью 50/50 (то есть, вероятность прибыльной сделки составляет 50% и вероятность убыточной сделки составляет 50%). И если бы каждая прибыльная сделка приносила ему 20 пунктов прибыли, а каждая убыточная 10 пунктов убытка, то математическое ожидание было бы положительным:
Математическое ожидание при тестировании торговых стратегий
Такой показатель как математическое ожидание очень важен при оценке эффективности торговой системы. Проводя тестирование торговых систем (на исторических данных) в тестере стратегий МТ4 (Metatrader 4), вы можете увидеть этот параметр в отчёте о результатах тестирования.
Отчёт тестера стратегий МТ4
Для корректного расчёта данного показателя следует брать достаточно глубокий срез статистики по совершённым сделкам. Как минимум необходимы данные о 100 — 150 закрытых сделках. В ином случае рассчитанный показатель не будет иметь должной объективности.
Кстати в МТ4, математическое ожидание вычисляется по формуле:
Мат.ожидание = (Общая прибыль + Общий убыток) / Кол-во сделок
Положительное математическое ожидание говорит трейдеру о том, что тестируемая им торговая стратегия является потенциально прибыльной. А отрицательное, соответственно, о том, что стратегия убыточна.
Что можно сделать для того, чтобы повысить математическое ожидание торговой стратегии? Самое очевидное, что можно для этого сделать, так это повысить соотношение Take Profit (TP) к Stop Loss (SL). Например, при соотношении TP/SL = 1 (размер профитов равен размеру убытков по каждой сделке), торговая стратегия показывает отрицательное матожидание, но стоит повысить это соотношение до TP/SL = 1,5…2, как стратегия сразу выходит в плюс.
Однако, здесь важно не перестараться. Ведь, хотя большинство авторов и рекомендуют соотношение TP/SL в пределах 2…3, но следует учитывать тот факт, что чем больший размер профита относительно лосса вы установите, тем больше в вашей статистике появится убыточных сделок. Увеличивая разрыв между значениями Stop Loss и Take Profit, вы тем самым, уменьшаете и вероятность того, что цена в итоге достигнет профита, а не столкнётся с лоссом.
Математическое ожидание в спортивном беттинге
Нашел сегодня любопытную статью все с того же ресурса, где я чаще всего провожу свое время, когда дело касается ставок на спорт. Поэтому не мог не оставить ссылку на первоисточник сегодняшней статьи. А поговорим мы сегодня о том, что такое математическое ожидание в спортивном беттинге и какую роль оно играет в этой области азартных игр.
Математическое ожидание в ставках на спорт означает среднее (ожидаемое) значение размера выигрыша по сделанному пари. Вычисление данного показателя несет определенную ценность для беттора при сравнении котировок букмекерских контор. Далее в статье вы узнаете, как вычисление математического ожидания может помочь при прогнозировании выигрыша в спортивных ставках.
Математическое ожидание в спортивном беттинге – это сумма, которую беттор может выиграть или проиграть при многочисленном заключении пари с одинаковым коэффициентом. Формула математического ожидания в ставках довольно проста и представляет собой следующее выражение: разность произведений значения вероятности выигрыша на сумму возможного выигрыша по ставке и значения вероятности проигрыша на сумму возможного проигрыша.
(Вероятность выигрыша * сумма выигрыша по ставке) – (вероятность проигрыша * сумма проигрыша по ставке).
Расчет математического ожидания наиболее просто увидеть в примере с подбрасыванием монетки. Допустим вы все время ставите на то, что выпадет решка. Вероятность выигрыша для вас составляет 50% (0.5), собственно аналогичному значению соответствует вероятность проигрыша, 50% (0.5). Сумма ставки соответствует 100 рублям. При выпадении решки ваш выигрыш составляет 110 рублей.
Рассчитываем математическое ожидание данной ставки: (0.5 * 110) – (0.5 * 100) = 5 рублей. Это означает, что если вы многократно будете ставить на то, что выпадет решка, ваш выигрыш в итоге в среднем составит 5 рублей.
Возьмем другой пример. Ожидается футбольный матч между командами Ливерпуль и Реал Мадрид. Букмекерская контора выставила на игру следующие котировки:
Рассчитаем математическое ожидание для ставки на победу Ливерпуля. Стоит оговорится заранее, что в формуле будут использоваться значения вероятности, рассчитанные на основании коэффициентов букмекерской конторы. У типстера либо беттора может быть своя, отличная от букмекера, модель вычисления вероятности исходов в матче.
Рассчитать вероятность, используя котировки оператора спортивных ставок, довольно просто. Для этого необходимо единицу разделить на коэффициент исхода:
Определили вероятность победы команды Ливерпуль, 0.303. Соответственно значение вероятности проигрыша составит 0.459 + 0.253 = 0.712. Сумму ставки, для примера, определим в 1 000 рублей. Тогда возможный выигрыш составит: 3.30 * 1 000 рублей – 1 000 рублей = 2 300 рублей.
Так в чем же истинная польза математического ожидания?
Необходимо понимать, что отрицательное математическое ожидание по ставке вовсе не означает, что данная ставка непременно окажется проигрышной. Также помните, что котировки букмекерских контор по своей природе являются субъективными. Если вычисленная вами вероятность исходов матча по собственной модели (к примеру, близкая к распределению Пуассона) отличается от значений вероятности исходов, заложенных в коэффициентах букмекера, то возможно вы сможете найти ставку с положительным математическим ожиданием и это повысит вероятность выигрыша от такой сделанной ставки.
Также, используя расчеты математического ожидания ставок, бетторы смогут дополнительно почерпнуть информацию о ценности котировок, предлагаемые их букмекером. Ставки с минимальным отрицательным математическим ожиданием означают, что данный букмекер закладывает в коэффициенты низкую маржу.
Матожидание как инструмент оценки предстоящего спортивного события
Каждый игрок, рассматривающий ставки на спорт не просто в качестве хобби, но и источника получения прибыли в долгосрочной перспективе, старается найти оптимальную стратегию игры, которая бы приносила прибыль на дистанции. Разовые выигрыши – лишь стечение обстоятельств, полагаться на них нет смысла.
Один из наиболее эффективных способов просчитать, насколько то или иное пари окажется удачным, является математическое ожидание. Благодаря его расчету удастся понять, сможет ли такое событие приносить доход в долгосрочной перспективе. Именно этим руководствуются опытные игроки, когда выбирают необходимое событие.
Особенности расчета математического ожидания
Расчет математических данных поможет выявить закономерность, а также определить, насколько Вам подходит игра в той или иной букмекерской конторе. Во внимание должно приниматься множество событий, что позволит оценить их перспективу на дистанции.
Просчитать же математическое ожидание достаточно просто. Необходимо использовать формулу, где вычисляется разность произведений положительного результата на его вероятность и отрицательного на его исход. Лучше всего математическое ожидание поможет отобразить формула:
В ней использованы следующие значения:
Собственно, S*K – S – это непосредственно чистый размер выигрыша. Формулу расчета математического ожидания не имеет смысла применять, если Вы делаете ставку только на одно событие. Благодаря ему удастся предугадать результат на дистанции. Именно в этом ценность представленной формы и способа расчета.
Попробуем разобрать математическое ожидание на конкретном примере из мира футбола. Например, предполагается встреча между дортмундской «Боруссией» и «Баварией». Букмекерская контора предлагает следующие варианты исхода и коэффициенты на них:
Попробуем рассчитать математическое ожидание для данного конкретного события. Один из самых сложных элементов в формуле – вероятность выигрыша ставки. Оценить его можно при помощи коэффициентов, которые предлагаются в букмекерской конторе. Делается это очень просто, достаточно 1 разделить на предложенную котировку.
В данном случае вероятность победы «Боруссии» будет 1/3.30 = 0.303 или же 30.3 %. Проведя аналогичные расчеты для двух других вариантов исхода, удастся увидеть, что победа «Баварии» оценивается в 45.9 %, а ничейный исход противостояния в 25.3 %.
Итак, попробуем оценить математическое ожидание в контексте победы дортмундской «Боруссии». Поскольку сразу 2 варианта исхода нас не устраивают, то необходимо просчитать их вероятность. Она составляет 71.2 %.
Для более удобного подсчета возьмем круглый размер ставки, например, 100 рублей. Итак, в случае победы «Боруссии» выигрыш составит 330 р. Однако затем вычитаем 100 руб. (размер ставки). Получается, что чистая прибыль с данного события – 230 рублей.
Такое утверждение рационально только для целого ряда событий. В одиночном противостоянии всегда есть вероятность сенсации и неожиданного результата, который не сможет просчитать ни одна статистическая программа. Несмотря на то, что спорт полон сюрпризов, определенные закономерности все же есть, поэтому их обязательно нужно учитывать, если Вы рассматриваете прогнозы в качестве главного и стабильного источника дохода для себя.
Положительное математическое ожидание для конкретного события вовсе не ожидает, что оно обязательно принесет доход. Однако в долгосрочной перспективе лучше выбирать события с положительным балансом, что станет залогом стабильной финансовой прибыли. Для правильного подсчета ожиданий крайне важно уметь верно подсчитывать вероятности исходов. Иногда сделать это действительно непросто из-за странных коэффициентов, которые предлагаются в букмекерских конторах. Среди математических факторов, которые необходимо учитывать игроку, выделим:
Правильный банкинг – это еще один секрет того, что ставки на спорт будут приносить стабильный доход и позволят вывести прибыль на качественно новый уровень.
Отрицательное математическое ожидание
Анти-Мартингейл
Как говорилось выше, отрицательное математическое ожидание вовсе не обязательно означает приговор. Да, вероятность наступления такого события ниже, но игрок сможет взять свое за счет уровня коэффициентов, который предлагается в той или иной конторе.
Часто клиент букмекерской конторы слепо верит в заранее выбранную стратегию и не готов меняться в случае отрицательных для него результатов. Для лучшей иллюстрации ситуации посмотрим, как ведут себя игроки в одной и той же ситуации. Допустим, проходит теннисный турнир, где встречается явный фаворит с крепким середняком, условные Надаль и Чорич. На победу испанца букмекерские конторы предлагают коэффициент 1.30, а вот триумф хорвата оценивается котировкой 3.70.
Итак, перед началом встречи обычный игрок размышляет приблизительно следующим образом – Надаль выше в мировом рейтинге, находится в хорошей форме, поэтому и должен одержать победу в данном противостоянии. Более опытный фанат берет во внимание следующие факторы:
Однако опытный гандикапер исходит из несколько другой точки зрения. Поскольку проведенные расчеты продемонстрировали, что вероятность победы Надаля составляет 70 %, то коэффициент 1.30 на его победу сложно назвать выгодным. Исследования демонстрируют, что котировка должна быть не менее 1.43, чтобы и на дистанции получать стабильную прибыль.
При этом вероятность успеха Чорира – 30 %, поскольку в теннисе невозможен ничейный исход противостояния. Несложные подсчеты дают понять, что даже коэффициент в районе 3.34 позволит со временем «выходить в ноль», а предложенные 3.70 так и вовсе принесут прибыль на дистанции.
Допустим, данное противостояние все же закончится победой Рафаэля Надаля. Однако в данном случае опытный игрок даже не обратит на это внимание, ведь просчитанное математическое ожидание наглядно доказывает, что подборка поединков с такими коэффициентами позволит рассчитывать на доход.
Большинство фанатов рассчитывают на легкую сиюминутную прибыль. В реальности же необходимо все просчитывать, чтобы минимизировать вероятность отрицательного исхода на дистанции. В данном случае отрицательное математическое ожидание складывается из-за того, что букмекер предлагает заниженные коэффициенты на одного из спортсменов. Да, в краткосрочной перспективе это с большой вероятностью может принести доход, однако если посмотреть на целую серию противостояний, то результат вряд ли окажется положительным и не порадует болельщиков.
Один из главных секретов успешной и действительно выигрышной игры – умение правильно сопоставить коэффициенты и шансы команд (соперников). Также всегда важно находить сразу несколько событий, чтобы ставки со временем начали приносить Вам доход.
В чем преимущества расчета математического ожидания?
Достаточно применить предложенную формулу, чтобы понять, сможет такое событие, а также аналогичные ему стать для Вас источником стабильного дохода. Результаты в мире спорта предугадать весьма сложно, но наука – вещь упрямая, против математического вычисления крайне сложно пойти.
Практика доказывает, что проведенные вычисления позволяют чувствовать себя уверенно. Вначале результаты могут складываться не лучшим образом, но со временем все должно уладиться. Даже профессиональные игроки отказываются от просчета математического ожидания, поскольку делают прогнозы достаточно хаотично. В логике их действий крайне сложно найти последовательность, что приводит к проигрышам.
Правильное распределение средств и поиск событий с выгодными коэффициентами – это задачи, которые на сегодняшний день под силу выполнить даже начинающим игрокам. Благодаря расчету математического ожидания также удастся выяснить, какие букмекерские конторы предлагают своим игрокам действительно выгодные коэффициенты, а кто из них явно не способен в полной мере удовлетворить требования аудитории. Такая информация крайне важна, ведь от уровня маржи и показателя котировок напрямую зависит сумма дохода каждого пользователя.
Вопреки распространенному мнению, вычисление показателя занимает лишь считанные секунды. Да, в лайве его просчитать достаточно сложно, ведь там коэффициенты меняются слишком быстро, хотя, если мы говорим о том же футболе, то это не выглядит невозможным. Правильный анализ математического ожидания – это:
Сейчас такой формат ставок на спорт становится все более популярным, ведь игроки хотят застраховать свои активы и минимизировать вероятность неудач. Стоит отметить, что математическое ожидание не исключает их вовсе, а спортивные противостояния – вещь в целом достаточно непредсказуемая. Прибыль же удастся получить за счет более частых выигрышей или ставок на события с высокими коэффициентами, которые, пусть и далеко не всегда являются успешными, зато за счет коэффициентов принесут доход.
Таким образом, преимущества расчета математического ожидания совершенно очевидны. Теперь спортивные прогнозы на длинной дистанции перестанут быть для Вас хаотичными и обретут системность, а небольшая неудача не станет вызовом для бюджета. Именно поэтому научно доказанная теория нашла столь активное применение в контексте ставок на спорт, в чем уже успели убедиться тысячи игроков, испробовавших ее для вычисления долгосрочных результатов.
Может ли математическое ожидание быть отрицательным числом
Математическим ожиданием (МО) случайной величины называют ее среднее значение, определяемое по следующим формулам.
Для случайных дискретных величин МО равно
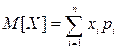
Для случайной непрерывной величины МО определяется выражением
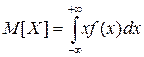
Математическое ожидание случайной величины представляет собой центр, около которого группируются частные значения ее.
Свойства математического ожидания:
а) математическое ожидание случайной величины может быть положительным и отрицательным, целым и дробным, и обладает размерностью случайной величины;
б) не все случайные величины имеют МО. Случайные величины не имеют МО, если 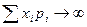
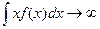
в) математическое ожидание постоянной величины равно самой постоянной величине, т.е. 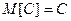
г) постоянную величину можно выносить за знак математического ожидания, т.е.
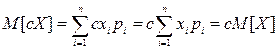
Частный случай математического ожидания. Пусть случайная величина X может принимать только два частных значения 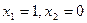
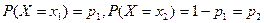
Откуда математическое ожидание 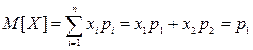
Следовательно, математическое ожидание такой случайной величины равна вероятности того, что случайная величина примет значение равное единице.
Пример 1: В технической системе имеется n элементов. Вероятность выхода из строя элемента в течении N часов работы равна p. Требуется определить математическое ожидание числа отказавших элементов в течении N часов работы.
Обозначим через X – случайную величину числа отказавших элементов, а через M[X] – математическое ожидание этого числа.
Для использования формулы математического ожидания определяем из условия задачи, что случайная величина X принимает частные значения 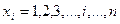
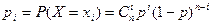
Тогда математическое ожидание числа отказавших элементов будет равно
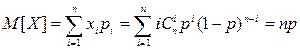
Отсюда следует, что если случайная величина X подчиняется биномиальному закону, то ее МО равно произведению числа опытов на вероятность появления события в одном опыте.
Часто происходит так, что после продолжительной серии успешных ставок беттор вдруг начинает «сыпаться». Та стратегия игры, которая давала результат вчера, сегодня приносит лишь одни убытки. Одна из основных ошибок бетторов состоит в том, что они полностью полагаются на свой успех в прогнозировании, при этом не рассчитывая реальные вероятности прохода тех или иных рынков.
Возьмем обычный пример, чтобы посмотреть, как себя ведут различные типы игроков.
К примеру, в теннисной игре встречаются Джокович и Вавринка. Букмекер дает на Джоковича коэффициент 1.3, а на Вавринку 3.70.
Как размышляет обычный игрок:
После этого делается ставка на победу серба.
Как размышляет опытный беттор:
После этого делается ставка на серба.
Как размышляет профессиональный гандикапер:
Допустим, что Джокович все же победил Вавринку в трех сетах. В этом случае первый игрок порадуется «легким» деньгам, опытный беттор оценит свое умение анализировать, а профессионал даже не обратит внимания на исход данного противостояния.
Дело в том, что по логике двух первых игроков ставка сделана верно, так как она прошла. При этом они не учитывают, того, что в 70% случаев эта ставка должна быть выигрышной и поэтому на дистанции у них не будет преимущества над линией. Если вероятность составляет 75%, а букмекер дает коэффициент, который равносилен 70% вероятности, то такая ставка будет с отрицательным математическим ожиданием. Можно получить от данных ставок сиюминутную прибыль, но со временем депозит будет проигран.
Вывод
При анализе вы должны не указать победителя предстоящей игры, а правильно оценить шансы соперников. Сопоставив шансы с коэффициентами букмекеров, можно понять, насколько такая ставка будет выгодна на дистанции.
При размещении ставок любого типа всегда существует определенная вероятность получения прибыли и риск потерпеть неудачу. Положительный исход сделки, и риск потерять деньги неразрывно связаны с математическим ожиданием. В данной статье мы подробно остановимся на этих двух аспектах трейдинга.
Математическое ожидание —среднее значениеслучайной величины при количестве выборок или количества её измерений (иногда говорят — количества испытаний) стремящимся к бесконечности.
Смысл в том, что положительное математическое ожидание ведет к положительной (с повышением прибыли) торговле, а нулевое или отрицательное математическое ожидание означают, что не нужно торговать вообще.
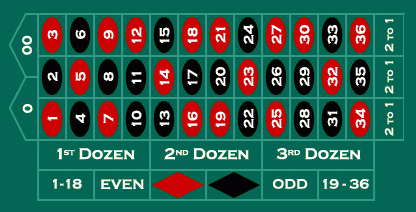
Что бы было легче разобраться в данном вопросе, давайте рассмотрим понятие математического ожидания при игре в рулетку. Пример с рулеткой очень прост для понимания.
Рулетка —азартная игра ( Крупье запускает шарик в противоположную сторону вращения колеса, с того номера на какой шарик упал в предыдущий раз, который должен упасть в одну из пронумерованных ячеек, сделав не менее трёх полных оборотов по колесу.
Ячейки, пронумерованные числами от 1 до 36, окрашены в чёрный и красный цвета. Номера расположены не по порядку, хотя цвета ячеек строго чередуются, начиная с 1 — красного цвета. Ячейка, обозначенная цифрой 0, окрашена в зелёный цвет и называется зеро
Рулетка- это игра с отрицательным математическим ожиданием. Все из-за поля зеро.«0», которое не является ни черным, ни красным.
Второй пример — знаменитые бинарные опционы. Вам дают сделать ставку, при удачном исходе вы забираете аж 90 процентов сверху от своей ставки, а при неудачном- теряете все 100. И дальше владельцам БО достаточно просто ждать, рынок и отрицательное мат ожидание сделают свое дело. А временная дисперсия даст надежду трейдеру бинарных опционов, что на данном рынке можно зарабатывать. Но это временно.
Человек сам может создать для себя систему. Сам может ограничить свой риск, и стараться забрать с рынка максимум возможной прибыли. (Причем если со вторым ситуация довольно спорная, то риск нужно контролировать очень четко.)
Чтобы понимать в каком направлении вас ведёт ваша стратегия необходимо ведение статистики. Трейдер должен знать:
Математическое ожидание (Е) = B * R – (1 – B) = B * (1 + R) –1
Чтобы примерно узнать свой итоговый заработок или убыток на счете (EE), к примеру, на дистанции в 1000 трейдов, воспользуемся формулой.
Где N — количество трейдов, которые мы планируем исполнить.
Для примера возмем начальные данные:
стоп лосс — 30 долларов.
профит — 100 долларов.
Количество сделок 30
Математическое ожидание отрицательное только при соотношении прибыльных и убыточных сделок (R) 20%/80% или хуже В остальных случаях положительное.
Пусть теперь профит будет 150. Тогда отрицательным мат ожидание будет при соотношении 16%/84%. Или ниже.
Вывод.
Что с этим делать? Начните вести статистику, если еще не начинали. Проверьте свои трейды, определите Ваше мат ожидание. Найдите то, что можно улучшить ( количество верных входов, добор профита, урезание убытков)