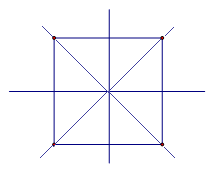
что такое оси симметрии в квадрате
Что такое осевая симметрия? Само слово «симметрия» имеет греческие корни и говорит о существующем определенном порядке расположения частей некого предмета, а также о его соразмерности.
Под симметрией понимается такое качество предметов, что их можно совместить друг с другом при некоторых преобразованиях.
Что такое симметрия
Наиболее часто это понятие встречается в геометрии. Объект считается симметричным, если после некоторых геометрических преобразований он смог сохранить свои первоначальные свойства.
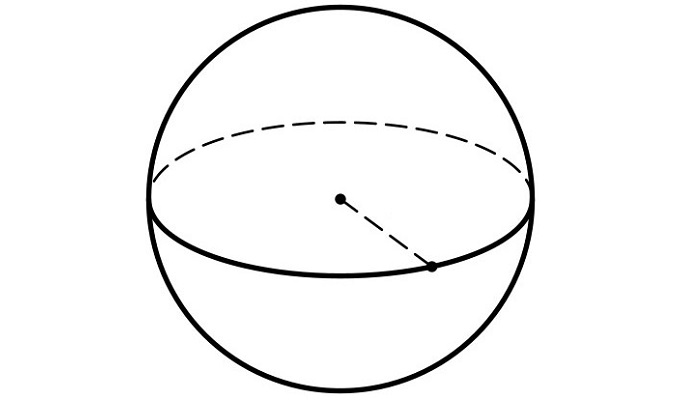
В качестве примера стоит рассмотреть обычный круг. Если его вращать вокруг условного центра, он сохранит свою форму и первоначальные характеристики. Поэтому этот геометрический предмет смело можно назвать симметричным.
Виды симметрии определяются возможными преобразованиями для данного объекта и его свойствами, которые в результате проведенных манипуляций должны сохраниться. В случае, когда это условие не соблюдается, можно утверждать о наличии асимметрии.
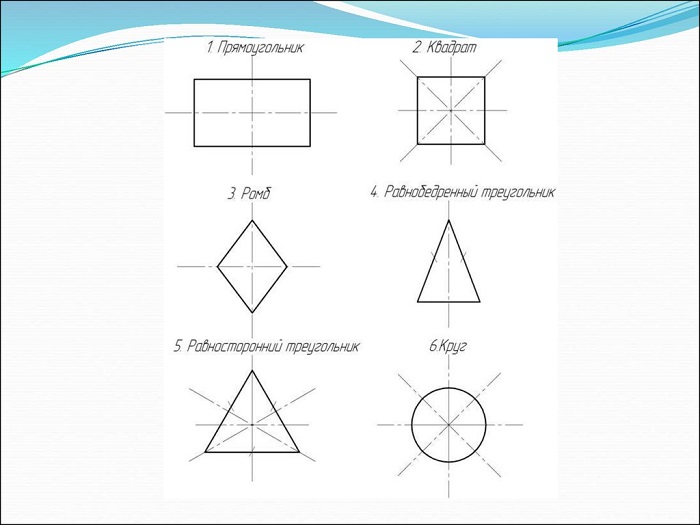
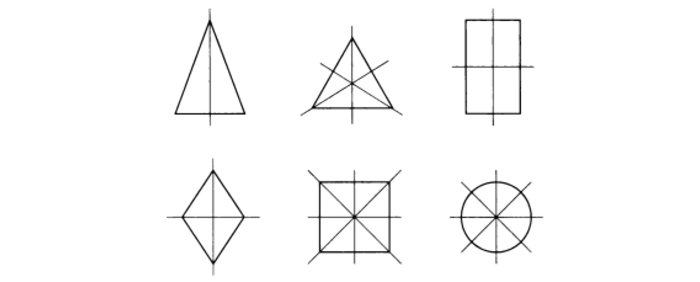
Рис. 1 Фигуры, обладающие симметричностью
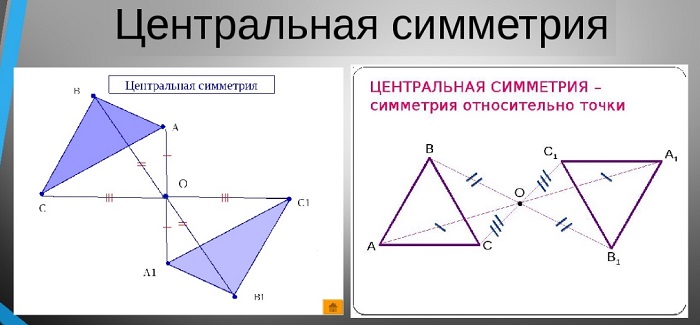
Центральная симметрия
Это явление относительно некой точки. Она представляет собой преобразование множества точек пространства или поверхности, во время которого ее центр всегда постоянен и не меняет своего положения.
Данный вид симметрии предполагает, что на равном расстоянии от ее центра располагаются два предмета, например, две точки. Если провести между ними условную прямую, они будут располагаться на ее противоположных концах, а середина этой прямой и будет являться осевым центром.
Если считать центр неподвижным и начать преобразовывать прямую (т. е. вращать ее относительно центральной точки), то точки на ее концах опишут две кривые. Все точки одной кривой будут иметь такие же симметричные точки на другой кривой.
Объекты, обладающие центром симметрии, представляют большой интерес для ученых. В геометрии насчитывается достаточно много таких объектов. К ним относятся прямые, отрезки, окружность, прямоугольник и др. Центрально симметричные объекты встречаются и в природе.
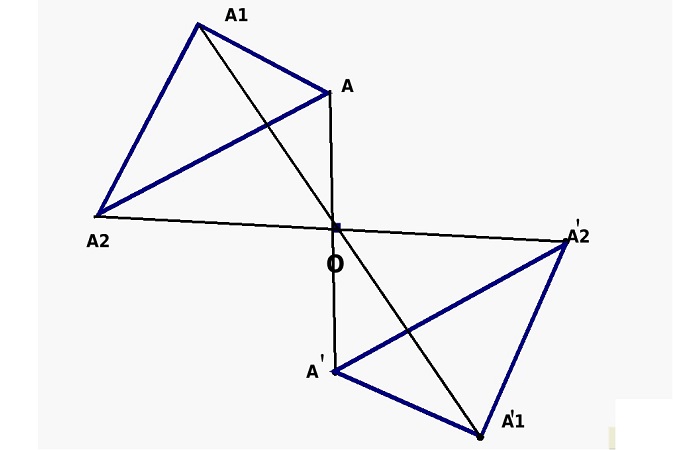
Рис. 2 Графическое представление центральной симметрии
Осевая симметрия
Это симметрия относительно прямой. В данном классе две точки симметричны относительно некой прямой, если она пересекает центр отрезка, соединяющего эти две точки и является перпендикуляром к нему. Любая точка прямой симметрична сама себе.
Рис. 3 Наглядное представление осевой симметрии
В качестве наглядно примера можно взять обычный бумажный лист, если его сложить пополам. Если через линию сгиба провести прямую – это и будет центром.
Определенная точка одной половины листы имеет такую же симметричную точку на другой его части, расположенную на перпендикуляре на таком же расстоянии от осевой линии. Одна часть листа тетради является по сути зеркальным отображением другой.
Рис. 4 Примеры осевой симметрии
Фигуры, имеющие несколько осей симметрии
Есть предметы и геометрические фигуры с некоторым числом осей. Для начала в качестве примера стоит рассмотреть прямоугольник и ромб, которые имеют две такие оси.
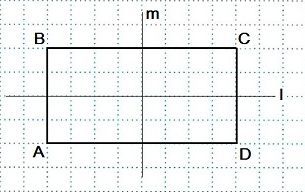
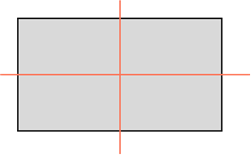
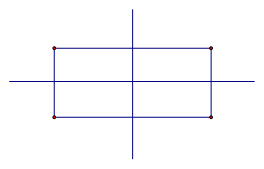
Две оси симметрии характерны для прямоугольника. Это прямые, которые проведены через точки, являющиеся серединами его противоположных сторон.
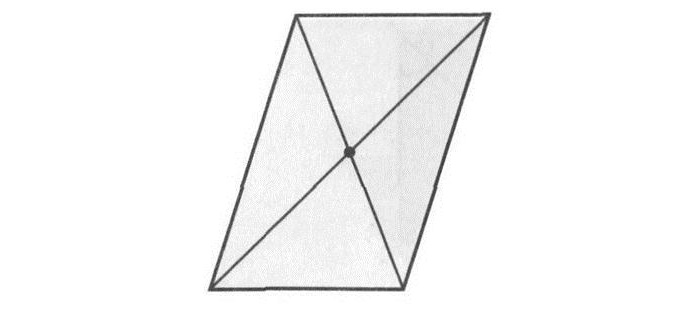
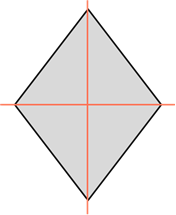
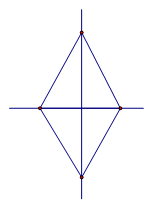
То же самое (наличие двух осей) присуще и ромбу. Оси являются прямыми, содержащими диагонали данной геометрической фигуры.
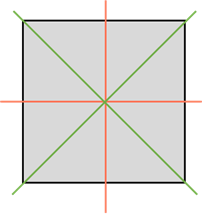
Интерес представляет и квадрат, у которого насчитывается четыре оси. Данная фигура является одновременно и ромбом, и прямоугольником. Остальные виды параллелограммов не имеют осей симметрии вообще.
Рис. 5 Оси симметрии ромба
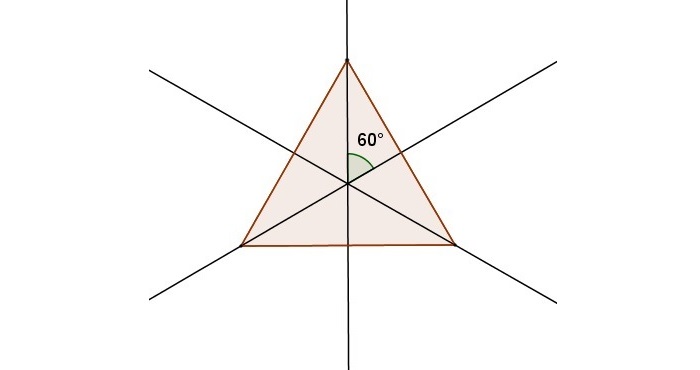
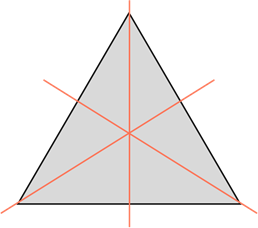
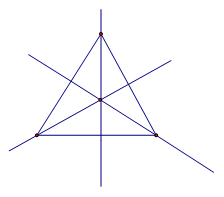
Единственной фигурой, у которой есть три оси симметрии, является равносторонний треугольник. Они представляют собой не что иное, как его медианы, линии соединяющие середины его сторон. Медианы равностороннего треугольник – это его и биссектрисы, и высоты.
Рис. 6 Оси симметрии равностороннего треугольника
В обычной жизни многие даже не задумываются о том, как часто они сталкиваются с различными видами симметрии. Это понятие характерно не только для мира математики.
Симметрия встречается в мире природы, архитектуре, в мире искусства и композиции, а также в других сферах человеческой жизни.
Осознание данного факта прошло долгий путь во времени, над ним задумывались великие умы на протяжении многих столетий. С древних времен и до настоящего времени определение этого понятия прошло долгий путь развития.
Симметрия
Урок 29. Наглядная геометрия 5–6 классы ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Симметрия»
Опыты с зеркалами, которые мы проводили на прошлом занятии, позволили нам прикоснуться к удивительному миру симметрии.
В переводе с греческого слово «симметрия» означает «соразмерность, пропорциональность, одинаковость в расположении частей».
Посмотрите на кленовый лист, бабочку, снежинку. Их объединяет то, что они симметричны. Если мы на каждом из рисунков начертим прямую вот таким образом…
А затем поставим зеркальце вдоль этой прямой на каждом рисунке, то отражённая в зеркале половинка фигуры дополнит её до целой (такой же, как исходная фигура).
Поэтому такая симметрия называется зеркальной (или осевой, если речь идёт о плоскости). Прямая, вдоль которой поставлено зеркало, называется осью симметрии.
Если симметричную фигуру сложить пополам вдоль оси симметрии, то её части совпадут.
С симметрией мы постоянно встречаемся в повседневной жизни. Люди используют симметрию в орнаментах, предметах быта, технике. Издавна человек использовал симметрию в архитектуре. Древним храмам, башням средневековых замков, современным зданиям она придаёт гармоничность, законченность. Симметрия также встречается в природе. Она создаёт ощущение порядка, гармонии, красоты.
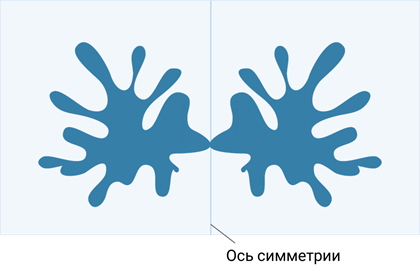
Давайте сделаем кляксу. Для этого на лист бумаги капнем чернил. Сложим лист вдвое, а затем разогнём. Линия сгиба листа является осью симметрии кляксы.
Получается, что клякса имеет одну (вертикальную) ось симметрии.
А вот у снежинки 6 линий сгиба и все они являются осями симметрии.
У геометрических фигур может быть одна или несколько осей симметрии, а может и не быть совсем.
Так, прямоугольник обладает двумя осями симметрии, каждая из которых проходит через середины двух его противоположных сторон. То есть, вырезав прямоугольник из бумаги и перегнув его по любой из двух осей симметрии, половинки фигуры совпадут.
Ромб также обладает двумя осями симметрии. Это прямые, которые содержат его диагонали.
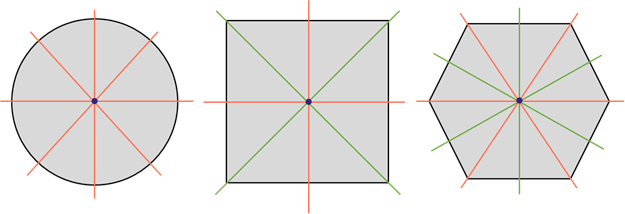
Квадрат имеет четыре оси симметрии. Две проходят через середины его противоположных сторон. И ещё две – это прямые, которые содержат его диагонали.
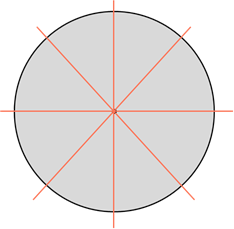
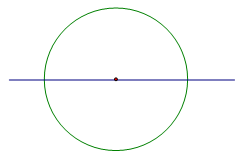
Круг. Его осью симметрии является любая прямая, которая проходит через его центр, то есть содержит диаметр круга. А значит, круг имеет бесконечно много осей симметрии
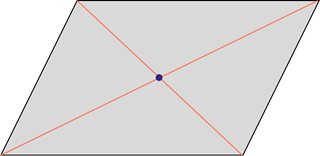
Теперь посмотрите на следующую фигуру. Это произвольный параллелограмм. У него нет ни одной оси симметрии.
У произвольного треугольника тоже нет осей симметрии.
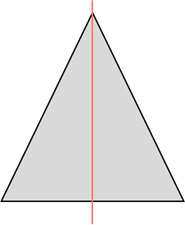
У равнобедренного треугольника есть одна ось симметрии.
У равностороннего (то есть у правильного) треугольника – три оси симметрии.
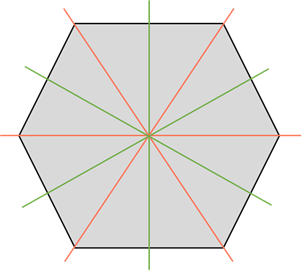
Теперь посмотрите на шестиугольник. У него три оси симметрии, которые проходят через противоположные вершины, и ещё три оси, которые проходят через середины противоположных сторон. То есть всего шесть осей симметрии.
Таким образом, мы можем сказать, что круг – «самая симметричная» фигура из рассмотренных, так как он имеет бесконечно много осей симметрии.
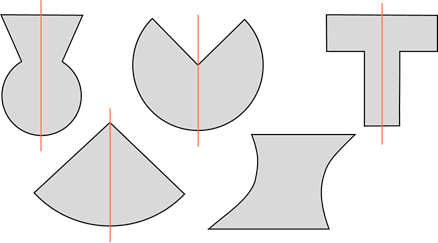
Сейчас давайте посмотрим на следующие фигуры и выясним, какая из них лишняя.
Итак, первая фигура напоминает замочную скважину. Она имеет одну ось симметрии.
Вторая фигура тоже имеет одну ось симметрии.
У третьей фигуры (в виде буквы Т) одна ось симметрии.
У четвёртой тоже одна. А вот пятая фигура не имеет ни одной оси симметрии. И поэтому она лишняя.
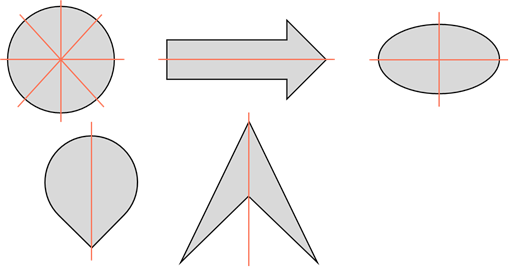
Теперь давайте посмотрим на следующие пять фигур. Что у них общего?
Первая фигура – круг. Выше мы выяснили, что у круга бесконечно много осей симметрии. Вторая фигура (в виде стрелки) имеет только одну ось симметрии. Третья фигура – эллипс. У эллипса две оси симметрии. Четвёртая фигура имеет одну ось симметрии. Пятая фигура тоже имеет одну ось симметрии. Каждая фигура имеет хотя бы одну ось симметрии.
На предыдущем занятии мы с вами проводили опыт с двумя плоскими зеркалами. С помощью составленного из двух зеркал калейдоскопа мы получали симметричные фигуры.
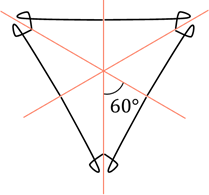
Давайте изобразим в виде прямых два зеркала под углом 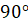
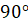
Посмотрите на рассмотренные выше фигуры, которые имеют две оси симметрии. Угол между осями равен 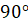
Если, например, мы поставим зеркала под углом 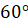
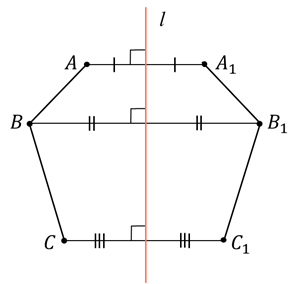
Давайте научимся точно строить отражение фигуры в зеркале. Представим, что прямая l – зеркало (или ось симметрии). Изобразим некоторую ломаную 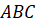
Итак, из вершин 
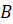
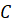

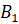
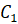
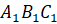
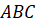
Можно сказать, что ломаная 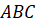
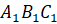
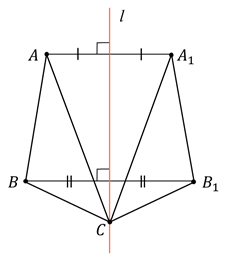
Построим с вами треугольник, симметричный треугольнику 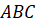
Из вершин 
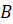

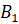
При этом точка 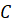
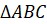
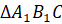
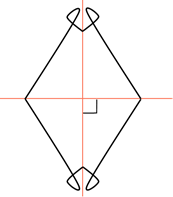
А сейчас посмотрите на рисунок.
Давайте выясним, симметрична ли точка 



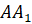
Потом с помощью линейки проверим, делит ли прямая l отрезок 

Значит, точки 

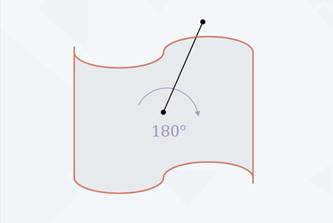
Кроме симметрии относительно прямой существует ещё симметрия относительно точки, так называемая центральная симметрия. Она характеризуется наличием центра симметрии – точки О, которая обладает определённым свойством. Можно сказать, что точка О является центром симметрии, если при повороте вокруг точки О на 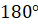
Понятие центральной симметрии распространяется и на трёхмерное пространство.
Проверить, является ли фигура центрально-симметричной или нет, можно с помощью обычной иголки и кальки. Наложим на нашу фигуру кальку. Затем, проколов фигуру в предполагаемом центре и обведя её контур, надо повернуть фигуру на 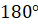
Сейчас посмотрите на плоские фигуры, которые имеют и центр симметрии, и оси симметрии.
Это круг. Выше мы сказали, что он имеет бесконечно много осей симметрии, каждая из которых содержит его диаметр. А вот центром симметрии круга является его центр.
Квадрат имеет четыре оси симметрии. Центром симметрии квадрата является точка пересечения его диагоналей.
У шестиугольника шесть осей симметрии. Центром его симметрии является точка пересечения его диагоналей.
Выше мы сказали, что произвольный параллелограмм не имеет ни одной оси симметрии. Но он имеет центр симметрии – это точка пересечения его диагоналей.
А вот, например, равнобедренный треугольник имеет ось симметрии, но не имеет центра симметрии. То же самое можно сказать и про пятиугольник, у которого есть оси симметрии, но центра симметрии нет.
Что называется осевой симметрией
Что такое осевая симметрия в геометрии
Симметрия – это свойство геометрических фигур отражаться. Симметрия относительно точки называется центральной. Осевая симметрия – это симметрия относительно прямой.
Если точка A и точка B симметричны относительно прямой n, то прямая называется осью симметрии n и проходит через середину отрезка AB. Обозначение осевой симметрии – Sn, таким образом симметрия точек A и B обозначается так:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Другое название осевой симметрии – вращательная – применяется в естественных науках. Данное понятие означает отражение предметов касательно поворотов вокруг прямой.
Свойства осевой симметрии
Теорема и доказательство
Осевая симметрия – это движение, то есть при преобразовании осевой симметрии расстояние между точками сохраняется.
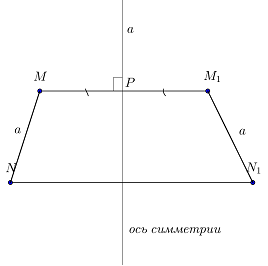
Если отрезок MN симметричен отрезку M1N1 относительно прямой a, то MN = M1N1.
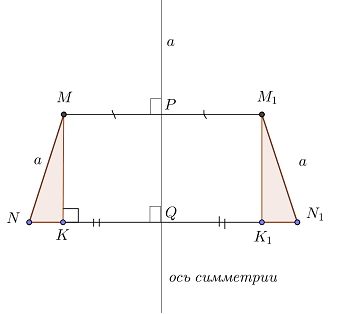
Чтобы доказать, что MN = M1N1, сделаем дополнительные построения:
Докажем, что прямоугольные треугольники MNK и M1N1K1 равны. Стороны MN и M1N1 являются гипотенузами данных треугольников, поэтому, нужно доказать равенство катетов.
Точка N отобразилась в точку N1, значит:
Итак, треугольники равны по двум катетам, следовательно, их гипотенузы равны, то есть MN = M1N1, что и требовалось доказать.
Фигуры, обладающие симметрией
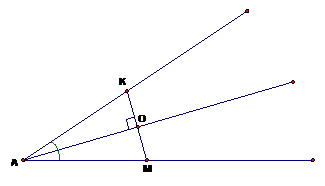
Осевой симметрией обладает угол, а биссектриса является осью симметрии.
Из произвольной точки одной стороны угла опустим перпендикуляр к биссектрисе и продлим его до другой стороны угла:
Рассмотрим Δ KAO и Δ MAO:
Отсюда следует, что KO = OM, поэтому точки K и M симметричны касательно биссектрисы угла.
Следовательно, равнобедренный треугольник тоже симметричен относительно биссектрисы, проведенной к основанию.
Равносторонний треугольник имеет три оси симметрии – биссектрисы, медианы, высоты каждого угла:
У прямоугольника две оси симметрии. Каждая из них проходит через середины противоположных сторон.
Ромб обладает двумя осями симметрии – это прямые, содержащие его диагонали.
Квадрат имеет 4 оси симметрии, так как он одновременно и ромб, и прямоугольник.
У окружности бесконечное множество осей симметрии – это все прямые, проведенные через центр круга.
Симметрия в повседневной жизни
Симметрия стала частью жизни человека уже в древние времена. Орнаменты с признаками зеркального отражения встречаются на античных зданиях, древнегреческих вазах. Свойство пропорционального расположения заимствовано в науку из природы.
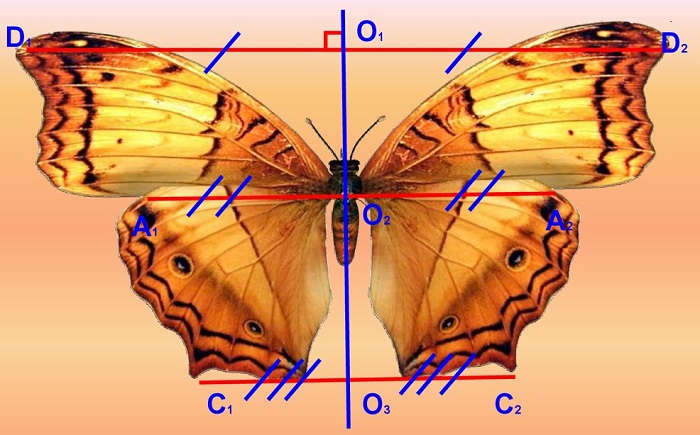
Зеркальное отражение часто встречается в живой и неживой природе. Этой характеристикой обладают снежинки. В растительном мире одинаково расположены противоположные элементы растений: большинство листьев зеркально отражаются сравнительно среднего стебля. В животном мире законы симметрии проявляются в наличии у животных правой и левой сторон. Большинство представителей фауны обладает парными частями тела: уши, лапы, глаза, крылья, рога. Ярким образцом зеркальной симметрии считается бабочка. Прямая, условно проведенная вдоль туловища насекомого по центру, является осью симметрии.
Поскольку человек – это часть природы, в своем творчестве он использует принцип симметрии. В искусстве свойство отражения применяется для создания красоты и гармонии. В архитектуре пропорциональность выполняет практическую функцию – придает зданиям устойчивость и надежность. В предметах быта можно встретить одинаковость в расположении частей узоров на коврах, принтов на ткани, рисунков обоев.
Стремление к созданию симметричного, предположительно, связано с притяжением Земли – гравитацией. Человек интуитивно считает симметрию формулой устойчивости. Принцип зеркального отражения играет важную роль в человеческой жизни. Тяга к гармонии и красоте побуждает человечество придерживаться правил пропорциональности.