что такое ось симметрии 4 класс у квадрата
Симметрия

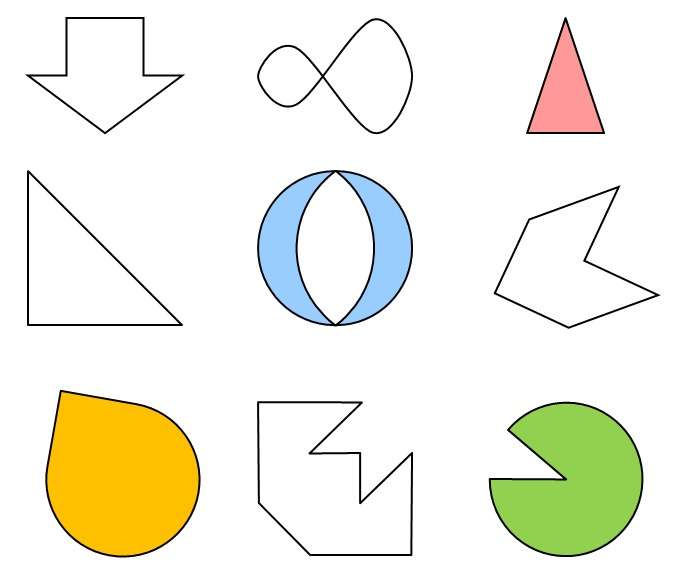
Некоторые фигуры не имеют симметрии, поэтому они и называются неправильными или же асимметричными. К таким относятся различные трапеции (кроме равнобедренной), треугольники (кроме равнобедренного и равностороннего) и другие.

Виды симметрии
Также обсудим некоторые виды симметрии, чтобы до конца изучить это понятие. Их разделяют так:
История симметрии
Само понятие симметрии часто бывает отправной точкой в теориях и гипотезах ученых древних времен, которые были уверены в математической гармонии мироздания, а также в проявлении божественного начала. Древние греки свято верили в то, что Вселенная симметрична, потому что симметрия великолепна. Человек очень давно использовал идею симметрии в своих познаниях картины мироздания.
В V веке до нашей эры Пифагор считал сферу самой совершенной формой и думал, что Земля имеет форму сферы и таким же образом движется. Также он полагал, что Земля движется по форме какого-то «центрального огня», вокруг которого должны были вращаться 6 планет (известные на то время), Луна, Солнце и все другие звезды.
А философ Платон считал многогранники олицетворением четырех природных стихий:
Из-за всех этих теорий правильные многогранники называют телами Платона.
Симметрией пользовались еще зодчие Древней Греции. Все их постройки были симметричны, об этом свидетельствуют изображения древнего храма Зевса в Олимпии.
Голландский художник М. К. Эшер также прибегал к симметрии в своих картинах. В частности, мозаика из двух птиц, летящих навстречу, стала основой картины «День и ночь».
Также и наши искусствоведы не пренебрегали правилами симметрии, что видно на примере картины Васнецова В. М. «Богатыри».
Симметрия геометрических фигур и тел
Рассмотрим внимательнее геометрические тела. Например, осью симметрии параболы является прямая, проходящая через ее вершину и рассекающая данное тело пополам. У этой фигуры имеется одна единственная ось.
Симметрия в природе
Природа поражает множеством примеров симметрии. Даже наше человеческое тело устроено симметрично. Два глаза, два уха, нос и рот расположены симметрично относительно центральной оси лица. Руки, ноги и все тело в общем устроено симметрично оси, проходящей через середину нашего тела.
Вывод
Урок математики. Тема: «Ось симметрии»
Разделы: Математика
Перед каждым лежат ножницы и лист бумаги.
– Возьмем лист бумаги, сложим его попалам и вырежем какую-нибудь фигурку. Теперь развернем лист и посмотрим на линию сгиба.
Вопрос: Какую функцию выполняет эта линия?
Предполагаемый ответ: Эта линия делит фигуру пополам.
Вопрос: Как расположены все точки фигуры на двух получившихся половинках?
Предполагаемый ответ: Все точки половинок находятся на равном расстоянии от линии сгиба и на одном уровне.
– Значит, линия сгиба делит фигурку пополам так, что 1 половинка является копией 2 половинки, т.е. эта линия непростая, она обладает замечательным свойством (все точки относительно ее находятся на одинаковом расстоянии), эта линия – ось симметрии.
– Вырезать снежинку, найти ось симметрии, охарактеризовать ее.
– Начертить в тетради окружность.
Вопрос: Определить, как проходит ось симметрии?
Предполагаемый ответ: По-разному.
Вопрос: Так сколько осей симметрии имеет окружность?
Предполагаемый ответ: Много.
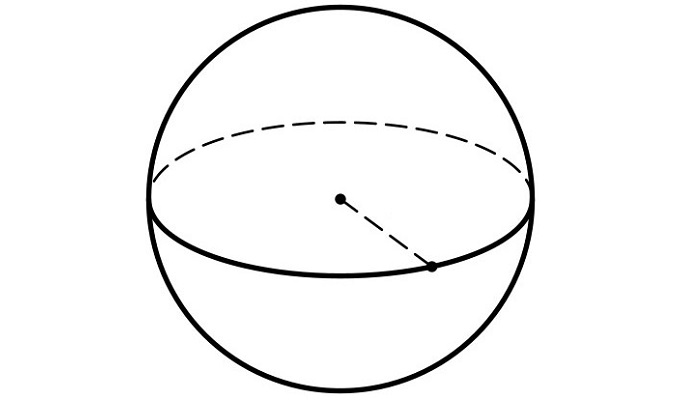
– Правильно, окружность имеет множество осей симметрии. Такой же замечательной фигурой является шар (пространственная фигура)
Вопрос: Какие еще фигуры имеют не одну ось симметрии?
Предполагаемый ответ: Квадрат, прямоугольник, равнобедренный и равносторонний треугольники.
– Рассмотрим объемные фигуры: куб, пирамиду, конус, цилиндр и т.д. Эти фигуры тоже имеют ось симметрии. Определите, сколько осей симметрии у квадрата, прямоугольника, равностороннего треугольника и у предложенных объемных фигур?
Раздаю учащимся половинки фигурок из пластилина.
– Используя полученную информацию, долепить недостающую часть фигурки.
Примечание: фигурка может быть и плоскостной, и объемной. Важно, чтобы учащиеся определили, как проходит ось симметрии, и долепили недостающий элемент. Правильность выполнения определяет сосед по парте, оценивает, насколько правильно проделана работа.
Из шнурка одного цвета на рабочем столе выложена линия (замкнутая, незамкнутая, с самопересечением, без самопересечения).
Задание 5 (групповая работа 5 мин).
– Определить визуально ось симметрии и относительно нее достроить из шнурка другого цвета вторую часть.
Правильность выполненной работы определяется самими учениками.
Перед учащимися представлены элементы рисунков
– Найдите симметричные части этих рисунков.
Для закрепления пройденного материала предлагаю следующие задания, предусмотренные на 15 мин.:
1. Прямая ОР – ось симметрии треугольника КОМ.
Назовите все равные элементы треугольника КОР и КОМ. Каков вид этих треугольников?
2. Начертите в тетради несколько равнобедренных треугольников с общим основанием равным 6 см.
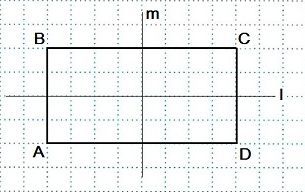
3. Начертите отрезок АВ. Постройте прямую перпендикулярную отрезку АВ и проходящую через его середину. Отметьте на ней точки С и D так, чтобы четырехугольник АСВD был симметричен относительно прямой АВ.
– Наши первоначальные представления о форме относятся к очень отдаленной эпохе древнего каменного века – палеолита. В течение сотен тысячелетий этого периода люди жили в пещерах, в условиях мало отличавшихся от жизни животных. Люди изготовляли орудия для охоты и рыболовства, вырабатывали язык для общения друг с другом, а в эпоху позднего палеолита украшали свое существование, создавая произведения искусства, статуэтки и рисунки, в которых обнаруживается замечательное чувство формы.
Когда произошел переход от простого собирания пищи к активному ее производству, от охоты и рыболовства к земледелию, человечество вступает в новый каменный век, в неолит.
Человек неолита обладал острым чувством геометрической формы. Обжиг и раскраска глиняных сосудов, изготовление камышовых циновок, корзин, тканей, позже – обработка металлов вырабатывали представления о плоскостных и пространственных фигурах. Неолитические орнаменты радовали глаз, выявляя равенство и симметрию.
– А где в природе встречается симметрия?
Предполагаемый ответ: крылья бабочек, жуков, листья деревьев…
– Симметрию можно наблюдать и в архитектуре. Строя здания, строители четко придерживаются симметрии.
Поэтому здания получаются такие красивые. Также примером симметрии служит человек, животные.
1. Придумать свой орнамент, изобразить его на листе формат А4 (можно нарисовать в виде ковра).
2. Нарисовать бабочек, отметить, где присутствуют элементы симметрии.
Урок «Математика и конструирование» по теме «Осевая симметрия». 4-й класс
Класс: 4
Цель занятия: дать представление об осевой симметрии; научить находить осевую симметрию в фигурах.
Задачи:
Формируемые УУД:
Методическое оснащение: ПК, интерактивная доска, презентация, у каждого ученика: одна из геометрических фигур (квадрат, прямоугольник, равносторонний и прямоугольный треугольники, круг), линейка, ножницы, цветная бумага; карточки с заданиями.
Ход урока
1. Организационный момент
Добрый день, ребята. Мы начинаем урок «Математика и конструирование». Пусть сегодняшний урок принесёт нам радость общения. Сегодня на уроке вас ожидает много интересных заданий и новых открытий! А вашими помощниками пусть будут внимание, целеустремлённость и ваша активная деятельность.
2. Мотивирование к учебной деятельности
— А знаете ли вы, что …
— А знаете ли вы, что…
— Во время сна рост увеличивается на 8 мм. Но после пробуждения он «возвращается» к прежним цифрам.
— А знаете ли вы, что …
— А знаете ли вы, что …
— Число 111 111 магическое! При умножении его на само себя получается такой лёгкий ответ 12 345 654 321.
— А знаете ли вы, что …
— 90% информации человек получает при помощи глаз. Отсюда и пошло выражение «Лучше один раз …»
3. Актуализация знаний
— Посмотрите небольшой видео-ролик и найдите закономерность.
— Что интересного вы заметили? (отражение в воде)
— А где еще отражаются предметы? (В зеркале).
— Подумайте, как в математике называется зеркальное отображение? (СИММЕТРИЯ)
— Отлично! Сформулируйте тему урока. (или нам поможет ребус). (Слайд Симметрия.)
— Тогда Давайте поставим перед собой цель урока.
— Назовите предметы, которые вы считаете СИММЕТРИЧНЫМИ. (запись на доске) не знаем…, не уверенны…
— В переводе с греческого языка симметрия звучит как «гармония», означая красоту.
Симметрия придает гармоничность, законченность.
4. Практическая работа. Введение в новую тему «Ось симметрии»
Исследование квадрата.
— У вас на столе лежат квадраты.
— Сложите квадрат пополам и четко прогладим линию сгиба.
— Покажите! Что мы наблюдаете?
— Какие получились части квадрата? (Одинаковые)
— Обведите цветным карандашом получившуюся прямую. Это и есть ось симметрии!
Вывод: в квадрате мы нашли ось симметрии. Ось симметрии делит фигуру на одинаковые равные части. Эти половинки совпадают.
— Давайте попробуем сложить квадрат вновь пополам, но по-другому.
— Обведите эту линию.
— Как еще можно сложить квадрат? (по диагонали)
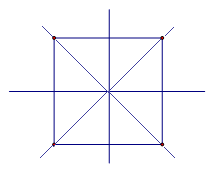
— Так сколько же осей симметрии у квадрата? (4)
— Правильно! Запишем это в таблицу
5. Физминутка (рисуем руками в воздухе)
Много ль надо нам, ребята,
Для умелых наших рук?
Нарисуем 2 квадрата,
А на них огромный круг.
А потом ещё кружочек,
Треугольный колпачок.
Вот и вышел очень, очень
Развесёлый чудачок!
— Подойдите к окну, Пусть отдохнут ваши глаза, посмотрите по сторонам, полюбуйтесь красотой зимнего дня. Возможно, вы увидите симметричные предметы.…. Перечислите. Продолжаем работать!
6. Работа в группах
Исследование разных геометрических фигур. Защита.
— Каждый должен работать на общий результат.
— Один говорит, другие слушают.
— Своё несогласие высказывай вежливо.
Ваша задача узнать, симметрична ли фигура? сколько осей симметрии имеет геом. фигура? Выступать будет один представитель от группы. Вам дается 1 мин на исследование. И 1 мин на выступление. Используете алгоритм для выступления №1. (и демонстрирует на большой фигуре.)
— Возьмите фигуры из конверта. Приступайте к исследованию.
— Что нужно сделать, чтобы провести ось симметрии? (перегнуть фигуры пополам)
— Проведите оси симметрии, если это возможно. Цветным карандашом.
— Слушаем представителя 1-й группы.
— Приглашаем представителя 2-й группы.
— Слушаем представителя 3-й группы.
— Слушаем представителя 4-й группы. (На доске заполняю результаты исследований в таблице)
ИТОГ. МОЛОДЦЫ. ВСЕ ГРУППЫ СПРАВИЛИСЬ С 1 ЗАДАНИЕМ.
— Назовите самую «несимметричную» фигуру. (Прям. Треугольник)
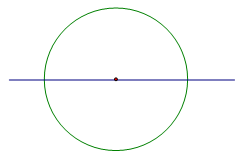
— Назовите самую «симметричную» фигуру. (круг)
— В Древней Греции круг считался венцом совершенства. И не случайно! У него больше всего осей симметрий!
7. Исследование в разных областях. Защита
— Мы выяснили, что в математике, не у всех фигур, но симметрия существует. Только ли в этой области она может быть?
— Оказывается, все в мире, всё построено по принципу симметрии. Древние греки считали, что Вселенная симметрична просто потому, что симметрия прекрасна. Используя красоту и гармонию природы, человек многое создал в мире симметрии своими руками. Об этих и многих других предметах мы сейчас и поговорим.
— Продолжим нашу исследовательскую работу.
— Возьмите конверт №2. Ознакомьтесь с темой исследования.
Приступайте к работе. Защита по алгоритму.
(Выступления групп. Выводы. Заполнение таблицы на доске.)
ИТОГ. МОЛОДЦЫ. ВСЕ ГРУППЫ СПРАВИЛИСЬ С 2 ЗАДАНИЕМ.
— Итак, мы доказали, что Симметрия- это не только красота. Симметричность формы нужна рыбе, чтобы плыть, птице, чтобы летать. Поэтому мы можем сделать вывод, что симметрия в природе неспроста: она ещё и полезна, т.е. целесообразна.
— К какой области можно отнести эти предметы, созданные руками человека?
8. Подведение итогов «Кластер». Оценивание
— Какие цели мы ставили в начале урока? …(Что такое симметрия? Где встречается?)
— Что вы выяснили для себя?
— Какие слова, словосочетания, связи, явления события … и т.д. возникают с этой темой?
Домашнее задание
— Ребята, это не все ОБЛАСТИ, где ВСТРЕЧАЕТСЯ СИММЕТРИЯ. Подумайте дома, подготовьте картинку, в какой области можно встретить симметрию. (Спорт, искусство,…и т.д.)
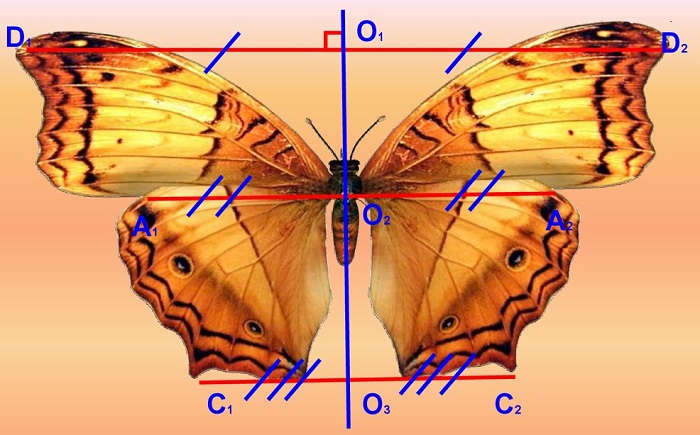
— Символом симметрии является БАБОЧКА.
Я предлагаю вам создать уникальный узор на крыльях бабочки или выполнить другой симметричный рисунок на выбор. Подойдите, возьмите, что вам больше нравится.
— Рассмотрите иллюстрацию к мультфильму. Что увидел Енот в пруду?
— А можно ли проверить, доказать, СИММЕТРИЧНЫ ли предметы из повседневной жизни, крупные, твёрдые… НЕ бумажные.
Что такое осевая симметрия? Само слово «симметрия» имеет греческие корни и говорит о существующем определенном порядке расположения частей некого предмета, а также о его соразмерности.
Под симметрией понимается такое качество предметов, что их можно совместить друг с другом при некоторых преобразованиях.
Что такое симметрия
Наиболее часто это понятие встречается в геометрии. Объект считается симметричным, если после некоторых геометрических преобразований он смог сохранить свои первоначальные свойства.
В качестве примера стоит рассмотреть обычный круг. Если его вращать вокруг условного центра, он сохранит свою форму и первоначальные характеристики. Поэтому этот геометрический предмет смело можно назвать симметричным.
Виды симметрии определяются возможными преобразованиями для данного объекта и его свойствами, которые в результате проведенных манипуляций должны сохраниться. В случае, когда это условие не соблюдается, можно утверждать о наличии асимметрии.
Рис. 1 Фигуры, обладающие симметричностью
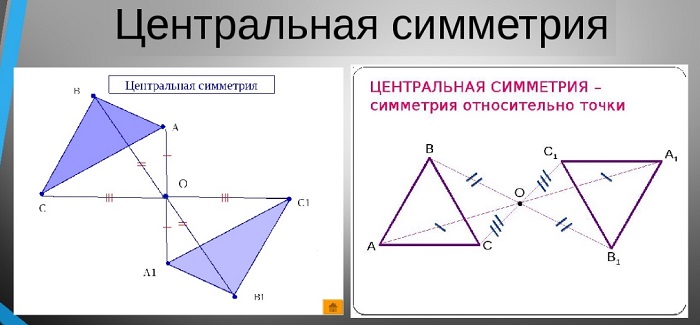
Центральная симметрия
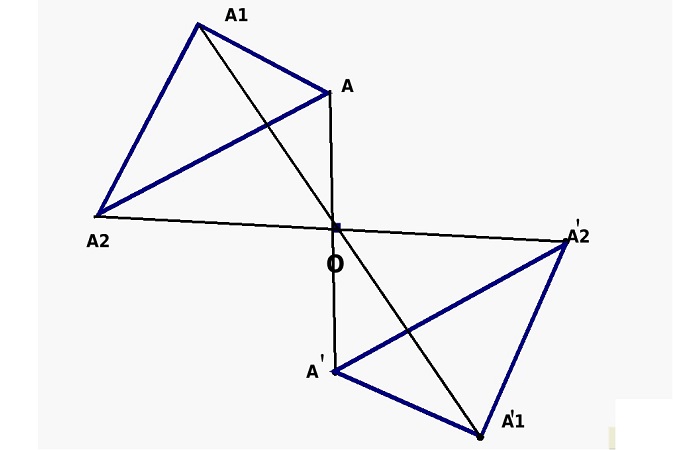
Это явление относительно некой точки. Она представляет собой преобразование множества точек пространства или поверхности, во время которого ее центр всегда постоянен и не меняет своего положения.
Данный вид симметрии предполагает, что на равном расстоянии от ее центра располагаются два предмета, например, две точки. Если провести между ними условную прямую, они будут располагаться на ее противоположных концах, а середина этой прямой и будет являться осевым центром.
Если считать центр неподвижным и начать преобразовывать прямую (т. е. вращать ее относительно центральной точки), то точки на ее концах опишут две кривые. Все точки одной кривой будут иметь такие же симметричные точки на другой кривой.
Объекты, обладающие центром симметрии, представляют большой интерес для ученых. В геометрии насчитывается достаточно много таких объектов. К ним относятся прямые, отрезки, окружность, прямоугольник и др. Центрально симметричные объекты встречаются и в природе.
Рис. 2 Графическое представление центральной симметрии
Осевая симметрия
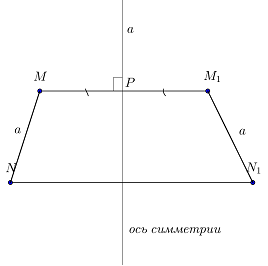
Это симметрия относительно прямой. В данном классе две точки симметричны относительно некой прямой, если она пересекает центр отрезка, соединяющего эти две точки и является перпендикуляром к нему. Любая точка прямой симметрична сама себе.
Рис. 3 Наглядное представление осевой симметрии
В качестве наглядно примера можно взять обычный бумажный лист, если его сложить пополам. Если через линию сгиба провести прямую – это и будет центром.
Определенная точка одной половины листы имеет такую же симметричную точку на другой его части, расположенную на перпендикуляре на таком же расстоянии от осевой линии. Одна часть листа тетради является по сути зеркальным отображением другой.
Рис. 4 Примеры осевой симметрии
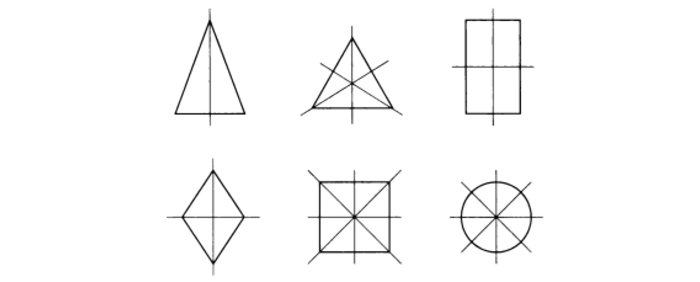
Фигуры, имеющие несколько осей симметрии
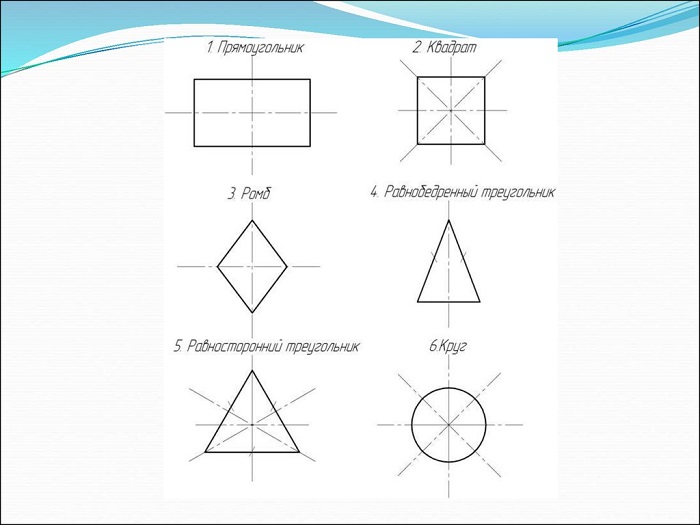
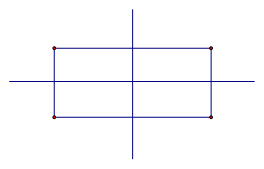
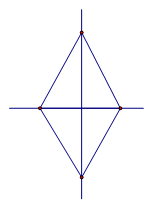
Есть предметы и геометрические фигуры с некоторым числом осей. Для начала в качестве примера стоит рассмотреть прямоугольник и ромб, которые имеют две такие оси.
Две оси симметрии характерны для прямоугольника. Это прямые, которые проведены через точки, являющиеся серединами его противоположных сторон.
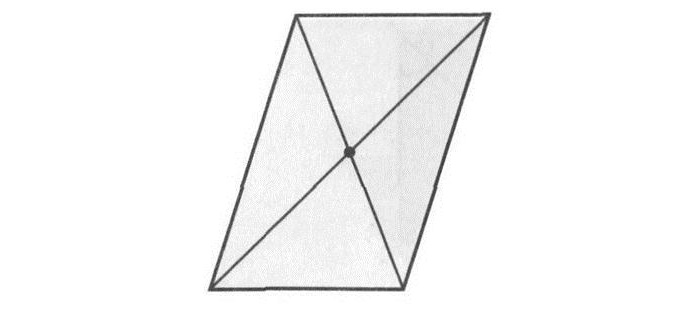
То же самое (наличие двух осей) присуще и ромбу. Оси являются прямыми, содержащими диагонали данной геометрической фигуры.
Интерес представляет и квадрат, у которого насчитывается четыре оси. Данная фигура является одновременно и ромбом, и прямоугольником. Остальные виды параллелограммов не имеют осей симметрии вообще.
Рис. 5 Оси симметрии ромба
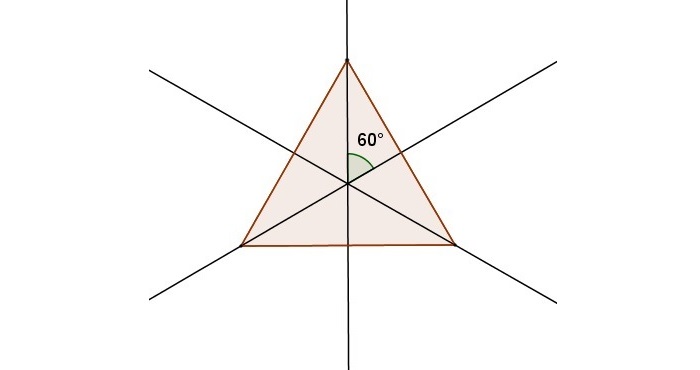
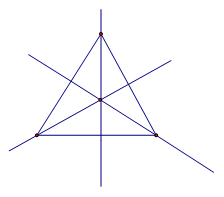
Единственной фигурой, у которой есть три оси симметрии, является равносторонний треугольник. Они представляют собой не что иное, как его медианы, линии соединяющие середины его сторон. Медианы равностороннего треугольник – это его и биссектрисы, и высоты.
Рис. 6 Оси симметрии равностороннего треугольника
В обычной жизни многие даже не задумываются о том, как часто они сталкиваются с различными видами симметрии. Это понятие характерно не только для мира математики.
Симметрия встречается в мире природы, архитектуре, в мире искусства и композиции, а также в других сферах человеческой жизни.
Осознание данного факта прошло долгий путь во времени, над ним задумывались великие умы на протяжении многих столетий. С древних времен и до настоящего времени определение этого понятия прошло долгий путь развития.
Что называется осевой симметрией
Что такое осевая симметрия в геометрии
Симметрия – это свойство геометрических фигур отражаться. Симметрия относительно точки называется центральной. Осевая симметрия – это симметрия относительно прямой.
Если точка A и точка B симметричны относительно прямой n, то прямая называется осью симметрии n и проходит через середину отрезка AB. Обозначение осевой симметрии – Sn, таким образом симметрия точек A и B обозначается так:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Другое название осевой симметрии – вращательная – применяется в естественных науках. Данное понятие означает отражение предметов касательно поворотов вокруг прямой.
Свойства осевой симметрии
Теорема и доказательство
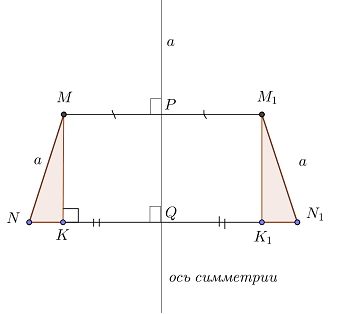
Осевая симметрия – это движение, то есть при преобразовании осевой симметрии расстояние между точками сохраняется.
Если отрезок MN симметричен отрезку M1N1 относительно прямой a, то MN = M1N1.
Чтобы доказать, что MN = M1N1, сделаем дополнительные построения:
Докажем, что прямоугольные треугольники MNK и M1N1K1 равны. Стороны MN и M1N1 являются гипотенузами данных треугольников, поэтому, нужно доказать равенство катетов.
Точка N отобразилась в точку N1, значит:
Итак, треугольники равны по двум катетам, следовательно, их гипотенузы равны, то есть MN = M1N1, что и требовалось доказать.
Фигуры, обладающие симметрией
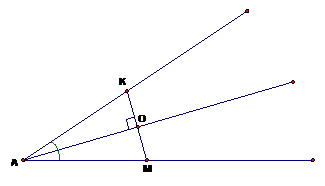
Осевой симметрией обладает угол, а биссектриса является осью симметрии.
Из произвольной точки одной стороны угла опустим перпендикуляр к биссектрисе и продлим его до другой стороны угла:
Рассмотрим Δ KAO и Δ MAO:
Отсюда следует, что KO = OM, поэтому точки K и M симметричны касательно биссектрисы угла.
Следовательно, равнобедренный треугольник тоже симметричен относительно биссектрисы, проведенной к основанию.
Равносторонний треугольник имеет три оси симметрии – биссектрисы, медианы, высоты каждого угла:
У прямоугольника две оси симметрии. Каждая из них проходит через середины противоположных сторон.
Ромб обладает двумя осями симметрии – это прямые, содержащие его диагонали.
Квадрат имеет 4 оси симметрии, так как он одновременно и ромб, и прямоугольник.
У окружности бесконечное множество осей симметрии – это все прямые, проведенные через центр круга.
Симметрия в повседневной жизни
Симметрия стала частью жизни человека уже в древние времена. Орнаменты с признаками зеркального отражения встречаются на античных зданиях, древнегреческих вазах. Свойство пропорционального расположения заимствовано в науку из природы.
Зеркальное отражение часто встречается в живой и неживой природе. Этой характеристикой обладают снежинки. В растительном мире одинаково расположены противоположные элементы растений: большинство листьев зеркально отражаются сравнительно среднего стебля. В животном мире законы симметрии проявляются в наличии у животных правой и левой сторон. Большинство представителей фауны обладает парными частями тела: уши, лапы, глаза, крылья, рога. Ярким образцом зеркальной симметрии считается бабочка. Прямая, условно проведенная вдоль туловища насекомого по центру, является осью симметрии.
Поскольку человек – это часть природы, в своем творчестве он использует принцип симметрии. В искусстве свойство отражения применяется для создания красоты и гармонии. В архитектуре пропорциональность выполняет практическую функцию – придает зданиям устойчивость и надежность. В предметах быта можно встретить одинаковость в расположении частей узоров на коврах, принтов на ткани, рисунков обоев.
Стремление к созданию симметричного, предположительно, связано с притяжением Земли – гравитацией. Человек интуитивно считает симметрию формулой устойчивости. Принцип зеркального отражения играет важную роль в человеческой жизни. Тяга к гармонии и красоте побуждает человечество придерживаться правил пропорциональности.