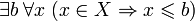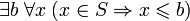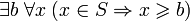что такое ограниченное множество
Ограниченное числовое множество
Ограниченное числовое множество
В математическом анализе, и прилегающих разделах математики, ограниченное множество — множество, которое в определенном смысле имеет конечный размер. Базовым является понятие ограниченности числового множества, которое обобщается на случай произвольного метрического пространства, а также на случай произвольного частично упорядоченного множества.
Содержание
Ограниченное числовое множество
Множество 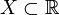
Множество 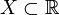
Примером ограниченного множества является отрезок 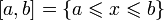
Вариации и обобщения
Ограниченное множество в метрическом пространстве
Пусть (X,ρ) — метрическое пространство. Множество 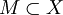
0) \; \forall x \in X (x \in M \Rightarrow \rho(a, x)
Множество, не являющееся ограниченным, называется неограниченным.
В отличие от числовой прямой, в произвольном метрическом пространстве нельзя ввести понятия ограниченного сверху и ограниченного снизу множеств.
Помимо понятия ограниченного множества для произвольного метрического пространства существует более специальное понятие вполне ограниченного множества. В случае числовых множеств это понятие совпадает с понятием ограниченного множества.
Ограниченность в частично упорядоченном множестве
Понятия ограниченного сверху, ограниченного снизу и просто ограниченного множества можно ввести в произвольном частично упорядоченном множестве. Эти определения буквально повторяют соответствующие определения для числовых множеств.
Пусть 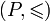
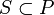
ограниченным снизу, если
Множество, ограниченное и сверху и снизу, называется ограниченным.
Ограниченное множество
В математическом анализе, и прилегающих разделах математики, ограниченное множество — множество, которое в определенном смысле имеет конечный размер. Базовым является понятие ограниченности числового множества, которое обобщается на случай произвольного метрического пространства, а также на случай произвольного частично упорядоченного множества. Понятие ограниченности множества не имеет смысла в общих топологических пространствах, без метрики.
Содержание
Ограниченное числовое множество
Множество вещественных чисел 



Множество вещественных чисел 



Множество 
Множество 
Примером ограниченного множества является отрезок 
неограниченного — множество всех целых чисел 


Вариации и обобщения
Ограниченное множество в метрическом пространстве
Пусть 



Множество, не являющееся ограниченным, называется неограниченным.
В отличие от числовой прямой, в произвольном метрическом пространстве нельзя ввести понятия ограниченного сверху и ограниченного снизу множеств.
Помимо понятия ограниченного множества для произвольного метрического пространства существует более специальное понятие вполне ограниченного множества. В случае числовых множеств это понятие совпадает с понятием ограниченного множества.
Ограниченность в частично упорядоченном множестве
Понятия ограниченного сверху, ограниченного снизу и просто ограниченного множества можно ввести в произвольном частично упорядоченном множестве. Эти определения буквально повторяют соответствующие определения для числовых множеств.
Пусть 


ограниченным снизу, если
Множество, ограниченное и сверху и снизу, называется ограниченным.
См. также
Полезное
Смотреть что такое «Ограниченное множество» в других словарях:
ОГРАНИЧЕННОЕ МНОЖЕСТВО — 1) О. м. в метрическом пространстве X(с метрикой ) множество А, диаметр к рого конечен. 2) О. м. в топологич. векторном пространстве Е(над полем k) множество В, к рое поглощается каждой окрестностью нуля U(т. е. существует такое ). М. И.… … Математическая энциклопедия
ВПОЛНЕ ОГРАНИЧЕННОЕ МНОЖЕСТВО — в метрическом пространстве то же, что вполне ограниченное подпространство данного метрич. пространства. См. Вполне ограниченное пространство. А. В. Архангельский … Математическая энциклопедия
Ограниченное числовое множество — В математическом анализе, и прилегающих разделах математики, ограниченное множество множество, которое в определенном смысле имеет конечный размер. Базовым является понятие ограниченности числового множества, которое обобщается на случай… … Википедия
множество — набор комплект — [http://www.rfcmd.ru/glossword/1.8/index.php?a=index d=4318] множество Одно из основных понятий современной математики, «произвольная совокупность определенных и различимых объектов, объединенных мысленно в единое… … Справочник технического переводчика
Множество — [set] одно из основных понятий современной математики, «произвольная совокупность определенных и различимых объектов, объединенных мысленно в единое целое». (Так определял множество основатель теории множеств, известный немецкий… … Экономико-математический словарь
МНОЖЕСТВО — см. Класс в логике. Философский энциклопедический словарь. М.: Советская энциклопедия. Гл. редакция: Л. Ф. Ильичёв, П. Н. Федосеев, С. М. Ковалёв, В. Г. Панов. 1983. МНОЖЕСТВО … Философская энциклопедия
Множество (тип данных) — У этого термина существуют и другие значения, см. Множество (значения). Множество тип и структура данных в информатике, является реализацией математического объекта множество. Данные типа множество позволяют хранить ограниченное число значений… … Википедия
ПОЛЯРНОЕ МНОЖЕСТВО — 1) П. м. аналитической функции f(z) комплексных переменных z=(z1. zn), п 1, такое множество Рточек нек рой области Dкомплексного пространства С n, что: а) f(z) голоморфна всюду в ; б) f(z) не продолжается аналитически ни в одну точку Р;в) для… … Математическая энциклопедия
генеральное множество (гм) текстов — объектом самого исследования выступает не сам подъязык, а некоторое множество текстов, являющееся в принципе бесконечным или, во всяком случае, открытым. Задается оно описательно, путем характеристики источников данных текстов. Именно они… … Толковый переводоведческий словарь
КОНСТРУКТИВНОЕ ПО ГЁДЕЛЮ МНОЖЕСТВО — множество, возникающее в описанном ниже процессе построения множеств. Пусть X множество и X. Рассмотрим язык 1 й ступени L(R, X), содержащий один 2 местный предикатный символ, обозначающий отношение R, и индивидные константы, обозначающие… … Математическая энциклопедия
Точечные множества
Множества, элементами которых являются точки, называются точечными множествами. Таким образом, можно говорить о точечных множествах на прямой, на плоскости, в каком-либо пространстве. Ради простоты мы ограничимся рассмотрением точечных множеств на прямой.
Между действительными числами и точками на прямой имеется тесная связь: каждому действительному числу можно отнести точку на прямой и обратно. Поэтому, говоря о точечных множествах, мы будем причислять к ним и множества, состоящие из действительных чисел — множества на числовой прямой. Обратно: для того чтобы задать точечное множество на прямой, мы будем обычно задавать координаты всех точек нашего множества.
Точечные множества (и, в частности, точечные множества на прямой) обладают рядом особых свойств, отличающих их от произвольных множеств и выделяющих теорию точечных множеств в самостоятельную математическую дисциплину. Прежде всего имеет смысл говорить о расстоянии между двумя точками. Далее, между точками на прямой можно установить соотношения порядка (левее, правее); в соответствии с этим говорят, что точечное множество на прямой является упорядоченным множеством. Наконец, как уже отмечалось выше, для прямой справедлив принцип Кантора; это свойство прямой принято характеризовать как полноту прямой.
Введем обозначения для простейших множеств на прямой.
Начнем с рассмотрения различных возможностей расположения множества в целом на прямой.
Ограниченные и неограниченные множества
Нетрудно видеть, что если — фиксированная точка на прямой, то множество будет ограничено в том и только в том случае., если расстояния от точки до любой точки не превосходят некоторого положительного числа.
Множества, ограниченные сверху и снизу
Ясно, что данное выше определение ограниченного множества эквивалентно следующему: множество точек на прямой называется ограниченным, если оно ограничено сверху и снизу. Несмотря на то, что эти два определения очень похожи друг на друга, между ними имеется существенное различие: первое основано на том, что между точками на прямой определено расстояние, а второе, что эти точки; образуют упорядоченное множество.
Верхняя и нижняя грань множества
Расположение точечного множества вблизи какой-либо точки на прямой
Укажем несколько примеров, поясняющих все эти понятия.
Пример 1. Пусть множество состоит из точек с координатами
Пример 4. Пусть множество состоит из всех точек с целыми координатами на прямой. Каждая точка является его изолированной точкой; множество не имеет предельных точек.
Теорема Больцано-Вейерштрасса
Всякое ограниченное бесконечное множество точек на прямой имеет хотя бы, одну предельную точку.
Ограниченные множества
Пусть непустое множество действительных чисел.
У ограниченного сверху множества существует сколь угодно много верхних границ. Действительно, если верхняя граница множества то для любого положительного число
также является верхней границей Аналогично, у ограниченного снизу множества существует сколь угодно много нижних границ.
С геометрической точки зрения ограниченность сверху множества означает наличие на числовой прямой такой точки что все точки множества расположены не правее Аналогично, ограниченность снизу множества означает наличие на числовой прямой такой точки что все точки множества расположены не левее, чем
С геометрической точки зрения ограниченность означает, что все точки множества содержатся в некотором отрезке числовой прямой.
Определение. Элемент называется наибольшим элементом множества если для любого справедливо неравенство Элемент называется наименьшим элементом множества если для любого справедливо неравенство
Очевидно, что если во множестве существует наибольший элемент, то это множество ограничено сверху, а если в существует наименьший элемент, то это множество ограничено снизу. Однако не каждое ограниченное сверху (снизу) множество имеет наибольший (наименьший) элемент. Например, множество ограничено сверху (например, числом однако в нем нет наибольшего элемента. Действительно, для любого число x» title=»z=\frac < x+1 > < 2 >> x» /> также принадлежит Аналогично можно показать, что ограничено снизу, но не имеет наименьшего элемента.
Пусть – ограниченное сверху множество. Через обозначим совокупность всех верхних границ множества Множество непусто и, как мы уже видели, неограничено сверху. Очевидно, однако, что ограничено снизу (например, любой элемент множества является нижней границей множества
Поставим следующий вопрос: существует ли во множестве наименьший элемент?
Это определение равносильно следующему.
Определение. Число называется верхней гранью множества если выполнены следующие два условия:
Первое условие этого определения означает, что является верхней границей множества а второе – что наименьшая из всех верхних границ, т. е. что никакое число не является верхней границей множества
Аналогично формулируется определение нижней грани.
Это определение равносильно следующему.
Определение. Число называется нижней гранью множества если выполнены следующие два условия:
Первое условие этого определения означает, что m является нижней границей множества а второе – что наибольшая из всех нижних границ, т. е. что никакое число m» title=»
Из определения верхней и нижней граней множества не следует сам факт их существования. Существование точных границ устанавливает следующая теорема.
Теорема (о существовании верхней грани). Каждое непустое ограниченное сверху множество имеет верхнюю грань. Пусть ограниченное сверху множество, а множество всех его верхних границ. Оба множества непустые, и для любых справедливо неравенство По аксиоме полноты множества действительных чисел, существует такое число что для любых справедливо неравенство Левое неравенство означает, что число является верхней границей множества т. е. а правое неравенство показывает, что наименьший элемент во множестве
Аналогично доказывается следующая
Теорема (о существовании нижней грани). Каждое непустое ограниченное снизу множество имеет нижнюю грань.
Понятие верхней (нижней) грани мы определили для ограниченного сверху (снизу) множества. Но не каждое множество ограничено сверху (снизу). Так, само множество действительных чисел неограничено сверху и снизу. В самом деле, для любого найдется такой, что M» title=»x > M» /> (например, Это означает, что никакое число не является верхней границей множества В случае если множество неограничено сверху, иногда пишут Аналогично, если множество неограничено снизу, то пишут Примером неограниченного снизу множества также может быть множество
Задание 1
Пусть 1. Доказать, что множество не имеет ни наименьшего, ни наибольшего элементов.
Действительно, для любого число x» title=»z=\frac < x+\sqrt < 2 >> < 2 >> x» /> также принадлежит следовательно, не имеет наибольшего элемента. Аналогично можно показать, что не имеет наименьшего элемента.
Действительно, всякие вещественные будут элементами множества и 0,» title=»\forall \varepsilon > 0,» /> по аксиоме полноты множества действительных чисел, существует такой что
т. е. какое бы вещественное число из мы не взяли, можно выбрать другое число из так, что оно будет находиться ближе к на числовой прямой.
Аналогично доказывается, что
Задание 2
Пусть непустые ограниченные множества неотрицательных действительных чисел, множество всевозможных чисел где Показать, что ограниченное множество, причём
По теореме о существовании верхней грани, из ограниченности и следует существование и Тогда справедливы неравенства: из которых следует, что т. е. является верхней границей множества Кроме того, поскольку и – множества неотрицательных действительных чисел, т. е. является нижней границей множества Отсюда следует, что множество ограничено.
Поскольку и соответственно являются верхними гранями множеств и справедливы неравенства 0\quad \forall x\in X:< M >_< 1 >-\varepsilon 0\quad \forall x\in X:< M >_< 1 >-\varepsilon
0\quad \forall y\in Y:< M >_< 2 >-\varepsilon 0\quad \forall y\in Y:< M >_< 2 >-\varepsilon из которых следует:
0\quad \forall x\in X\quad \forall y\in Y:» title=»\forall < \varepsilon >_< 1 >,< \varepsilon >_ < 2 >> 0\quad \forall x\in X\quad \forall y\in Y:» />
Обозначим:
Получим неравенство
0\quad \forall x\in X\quad \forall y\in Y:< M >_< 1 >< M >_< 2 >—< \varepsilon >_ < 3 >0\quad \forall x\in X\quad \forall y\in Y:< M >_< 1 >< M >_< 2 >—< \varepsilon >_ < 3 >. Из него и из неравенства следует, что что и требовалось доказать.
Забегая вперёд, при рассмотрении следующего задания используем материал урока «Определение и элементарные свойства».
Вполне ограниченное множество
Связанные понятия
В математическом анализе, и прилегающих разделах математики, ограниченное множество — множество, которое в определенном смысле имеет конечный размер. Базовым является понятие ограниченности числового множества, которое обобщается на случай произвольного метрического пространства, а также на случай произвольного частично упорядоченного множества. Понятие ограниченности множества не имеет смысла в общих топологических пространствах, без метрики.
В математике покрывающим множеством для последовательности целых чисел называется множество простых чисел, таких, что каждый член последовательности делится по меньшей мере на одно число множества.
В теории множеств, разделе математики, урэлемент или ур-элемент (от немецкой приставки ur- обозначающей «изначальный» или «исходный») — это объект (конкретный или абстрактный), который не является множеством, но который может быть элементом множества. Урэлементы иногда называются «атомами».
В теории вероятностей два случайных события называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. Аналогично, две случайные величины называют независимыми, если известное значение одной из них не дает информации о другой.
В теории множеств и смежных с ней областях математики под универсумом фон Неймана (обозначается V), или иерархией множеств по фон Нейману, понимается класс, образованный наследственными фундированными множествами. Такая совокупность, формализуемая теорией множеств Цермело-Френкеля (ZFC) часто используется в качестве интерпретации или обоснования ZFC-аксиом.
Говорят, что семейство графов имеет ограниченное расширение, если все его миноры ограниченной глубины являются редкими графами. Много естественных семейств редких графов имеют ограниченное расширение. Близкое, но более сильное свойство, полиномиальное расширение, эквивалентно существованию теорем разбиения для этих семейств. Семейства с этими свойствами имеют эффективные алгоритмы для задач, в которые входят задача поиска изоморфного подграфа и проверка моделей для теории первого порядка для графов.