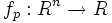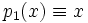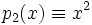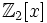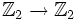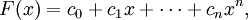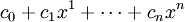что такое однородный многочлен

однородный многочлен

Смотреть что такое «однородный многочлен» в других словарях:

ОДНОРОДНЫЙ МНОГОЧЛЕН — многочлен, у всех членов которого сумма показателей степеней входящих в него переменных (неизвестных) одинакова. Напр.: x5+4x3y2 3xy4 … Большой Энциклопедический словарь

Однородный многочлен — многочлен, все одночлены которого имеют одинаковую полную степень. Любая алгебраическая форма является однородным многочленом. Примеры однородный многочлен однородный многочлен однородный многочлен неоднородный многочлен … Википедия

ОДНОРОДНЫЙ МНОГОЧЛЕН — многочлен, у всех членов к рого сумма показателей степеней входящих в него переменных (неизвестных) одинакова. Напр.: х5+ 4х3у2 3ху4 … Естествознание. Энциклопедический словарь

Многочлен Лорана — В математике, многочлены или полиномы от одной переменной функции вида где ci фиксированные коэффициенты, а x переменная. Многочлены составляют один из важнейших классов элементарных функций. Изучение полиномиальных уравнений и их решений… … Википедия

Общий метод решета числового поля — (англ. general number field sieve, GNFS) метод факторизации натуральных чисел. Является наиболее эффективным алгоритмом факторизации чисел длиной более 110 десятичных знаков. Сложность алгоритма оценивается эвристической формулой[1] Метод… … Википедия

Двучлен — В математике, многочлены или полиномы от одной переменной функции вида где ci фиксированные коэффициенты, а x переменная. Многочлены составляют один из важнейших классов элементарных функций. Изучение полиномиальных уравнений и их решений… … Википедия

Моном — В математике, многочлены или полиномы от одной переменной функции вида где ci фиксированные коэффициенты, а x переменная. Многочлены составляют один из важнейших классов элементарных функций. Изучение полиномиальных уравнений и их решений… … Википедия

Полином — В математике, многочлены или полиномы от одной переменной функции вида где ci фиксированные коэффициенты, а x переменная. Многочлены составляют один из важнейших классов элементарных функций. Изучение полиномиальных уравнений и их решений… … Википедия

Источник

ОДНОРОДНЫЙ МНОГОЧЛЕН

Смотреть что такое «ОДНОРОДНЫЙ МНОГОЧЛЕН» в других словарях:

ОДНОРОДНЫЙ МНОГОЧЛЕН — многочлен, у всех членов которого сумма показателей степеней входящих в него переменных (неизвестных) одинакова. Напр.: x5+4x3y2 3xy4 … Большой Энциклопедический словарь

Однородный многочлен — многочлен, все одночлены которого имеют одинаковую полную степень. Любая алгебраическая форма является однородным многочленом. Примеры однородный многочлен однородный многочлен однородный многочлен неоднородный многочлен … Википедия

однородный многочлен — многочлен, у всех членов которого сумма показателей степеней входящих в него переменных (неизвестных) одинакова. Например: х5+4х3у2 3ху4. * * * ОДНОРОДНЫЙ МНОГОЧЛЕН ОДНОРОДНЫЙ МНОГОЧЛЕН, многочлен, у всех членов которого сумма показателей… … Энциклопедический словарь

Многочлен Лорана — В математике, многочлены или полиномы от одной переменной функции вида где ci фиксированные коэффициенты, а x переменная. Многочлены составляют один из важнейших классов элементарных функций. Изучение полиномиальных уравнений и их решений… … Википедия

Общий метод решета числового поля — (англ. general number field sieve, GNFS) метод факторизации натуральных чисел. Является наиболее эффективным алгоритмом факторизации чисел длиной более 110 десятичных знаков. Сложность алгоритма оценивается эвристической формулой[1] Метод… … Википедия

Двучлен — В математике, многочлены или полиномы от одной переменной функции вида где ci фиксированные коэффициенты, а x переменная. Многочлены составляют один из важнейших классов элементарных функций. Изучение полиномиальных уравнений и их решений… … Википедия

Моном — В математике, многочлены или полиномы от одной переменной функции вида где ci фиксированные коэффициенты, а x переменная. Многочлены составляют один из важнейших классов элементарных функций. Изучение полиномиальных уравнений и их решений… … Википедия

Полином — В математике, многочлены или полиномы от одной переменной функции вида где ci фиксированные коэффициенты, а x переменная. Многочлены составляют один из важнейших классов элементарных функций. Изучение полиномиальных уравнений и их решений… … Википедия

Источник

ОДНОРОДНЫЙ МНОГОЧЛЕН

Смотреть что такое «ОДНОРОДНЫЙ МНОГОЧЛЕН» в других словарях:

Однородный многочлен — многочлен, все одночлены которого имеют одинаковую полную степень. Любая алгебраическая форма является однородным многочленом. Примеры однородный многочлен однородный многочлен однородный многочлен неоднородный многочлен … Википедия

однородный многочлен — многочлен, у всех членов которого сумма показателей степеней входящих в него переменных (неизвестных) одинакова. Например: х5+4х3у2 3ху4. * * * ОДНОРОДНЫЙ МНОГОЧЛЕН ОДНОРОДНЫЙ МНОГОЧЛЕН, многочлен, у всех членов которого сумма показателей… … Энциклопедический словарь

ОДНОРОДНЫЙ МНОГОЧЛЕН — многочлен, у всех членов к рого сумма показателей степеней входящих в него переменных (неизвестных) одинакова. Напр.: х5+ 4х3у2 3ху4 … Естествознание. Энциклопедический словарь

Многочлен Лорана — В математике, многочлены или полиномы от одной переменной функции вида где ci фиксированные коэффициенты, а x переменная. Многочлены составляют один из важнейших классов элементарных функций. Изучение полиномиальных уравнений и их решений… … Википедия

Общий метод решета числового поля — (англ. general number field sieve, GNFS) метод факторизации натуральных чисел. Является наиболее эффективным алгоритмом факторизации чисел длиной более 110 десятичных знаков. Сложность алгоритма оценивается эвристической формулой[1] Метод… … Википедия

Двучлен — В математике, многочлены или полиномы от одной переменной функции вида где ci фиксированные коэффициенты, а x переменная. Многочлены составляют один из важнейших классов элементарных функций. Изучение полиномиальных уравнений и их решений… … Википедия

Моном — В математике, многочлены или полиномы от одной переменной функции вида где ci фиксированные коэффициенты, а x переменная. Многочлены составляют один из важнейших классов элементарных функций. Изучение полиномиальных уравнений и их решений… … Википедия

Полином — В математике, многочлены или полиномы от одной переменной функции вида где ci фиксированные коэффициенты, а x переменная. Многочлены составляют один из важнейших классов элементарных функций. Изучение полиномиальных уравнений и их решений… … Википедия

Источник

Алгебра и начала математического анализа. 10 класс

Конспект урока

Алгебра и начала математического анализа, 10 класс

Урок №13. Многочлены от нескольких переменных.

Перечень вопросов, рассматриваемых в теме

1) определение многочлена от нескольких переменных;

2) понятие симметрических многочленов;

3) формулы сокращенного умножения для старших степеней;

5) метод неопределенных коэффициентов.

Многочлен Р(х;у) называют однородным многочленом n-й степени, если сумма показателей степеней переменных в каждом члене многочлена равна n. Если Р(х;у) — однородный многочлен, то уравнение Р(х;у) = 0 называют однородным уравнением.

Многочлен Р(х;у) называют симметрическим, если он сохраняет свой вид при одновременной замене х на у и у на х.

Уравнение Р(x;y) = а, где , называютсимметрическим, если Р(х;y) — симметрический многочлен.

Треугольник Паскаля —бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Назван в честь Блеза Паскаля.

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.

Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.

Теоретический материал для самостоятельного изучения

Многочлены от нескольких переменных можно складывать, вычитать, перемножать, возводить в натуральную степень, разлагать на множители — это вам известно из курса алгебры 7—9-го классов. Этот урок позволит нам несколько расширить знания о многочленах.

Воспользуемся методом группировки

(x+y+z+u) 2 =((x+y)+(z+u)) 2 = (x+y) 2 +2(x+y)(z+u)+(z+u) 2 = x 2 +y 2 +z 2 +u 2 +2(xy+xz+xu+yz+yu+zu).

Итак, мы получили (x+y+z+u) 2 = x 2 +y 2 +z 2 +u 2 +2(xy+xz+xu+yz+yu+zu).

Среди многочленов от двух переменных выделяют однородные и симметрические многочлены.

Многочлен Р(х;у) называют однородным многочленом n-й степени, если сумма показателей степеней переменных в каждом члене многочлена равна n. Если Р(х;у) — однородный многочлен, то уравнение Р(х;у) = 0 называют однородным уравнением.

1) р(х; у)=2х+3у – однородный многочлен первой степени; соответственно 2х+3у=0 – однородное уравнение первой степени.

2) р(х; у)=3х 2 +5ху-7у 2 — однородный многочлен второй степени; соответственно 3х 2 +5ху-7у 2 =0 — однородное уравнение второй степени.

4) p(x; y)= a_nx n +a_n-1x n-1 y+a_n-2x n-2 y 2 ₊…+a₁xy n-1 +a₀y n — общий вид однородного многочлена n-й степени.

Рассмотрим еще один метод разложения многочленов на множители-

метод неопределенных коэффициентов. Суть метода неопределённых коэффициентов состоит в том, что вид сомножителей, на которые разлагается данный многочлен, угадывается, а коэффициенты этих сомножителей (также многочленов) определятся путём перемножения сомножителей и приравнивания коэффициентов при одинаковых степенях переменной. Теоретической основой метода являются следующие утверждения

Пример 3. Разложить на множители многочлен

3 x 3 – x 2 – 3 x + 1.

Решая эту систему, получаем: a = 3, p = –1, b = 2, c = –1. Итак, многочлен 3 x 3 – x 2 – 3 x + 1 разлагается на множители: 3 x 3 – x 2 – 3 x + 1 = ( x – 1)(3 x 2 + 2 x – 1).

Стоит отметить, что существует достаточно изящный способ решения однородных уравнений. Поясним его суть на примере.

Далее последовательно находим:

Если z=1, то , т.е. у=х. Это значит, что любая пара вида (t; t) является решением заданного однородного уравнения. Между прочим, и отмеченная нами ранее пара (0; 0) также входит в указанный перечень решений.

Ответ: (t; t), где t- любое действительное число.

Теорема. Любой симметрический многочлен Р(х;у) можно представить в виде многочлена от ху и х+у.

x 4 +y 4 = 2xy(x 2 +y 2 )-(x 4 +y 4 )+3(xy) 2 и т.д.

Уравнение Р(x;y) = а, где , называют симметрическим, если Р(х;y) — симметрический многочлен. Мы с вами рассматривали его на предыдущем уроке.

А теперь перейдем к такому понятию как бином Ньютона.

Давайте вслед за Ньютоном попробуем ее вывести, чтобы затем применять.

Вы наверняка помните (или, по крайней мере, должны помнить), формулы сокращенного умножения для квадрата и куба суммы двух слагаемых (такая сумма называется «бином», по-русски – двучлен.

(a+b) 3 =a 3 +3a 2 b+3ab 2 +b 3

Если вы забыли эти формулы, можно их получить напрямую, раскрыв скобки в очевидных равенствах

Может быть, вам приходил в голову вопрос: можно ли (без компьютера) получить формулы типа для биномов четвертой степени, пятой, десятой – какой угодно?

Давайте попробуем дойти напрямую хотя бы до пятой степени, а там, может быть, окажется «рояль в кустах» (для порядка будем размещать слагаемые в правой части по убыванию степени а, она убывает от максимума до нуля):

(a+b) 4 =(a+b) 3 (a+b)=(a 3 +3a 2 b+3ab 2 +b 3 )(a+b)=a 4 +4a 3 b+6a 2 b 2 +4ab 3 +b 4

(a+b) 5 =(a+b) 4 (a+b)=(a 4 +4a 3 b+6a 2 b 2 +4ab 3 +b 4 )(a+b)=a 5 +5a 4 b+10a 3 b 2 +10a 2 b 3 +5ab 4 +b 5

Теперь отдельно выпишем численные коэффициенты в правых частях формул при возведении бинома в заданную степень:

Легко проверить, что выписанные на численные коэффициенты – это строчки треугольника Паскаля, начиная с третьей. Этот «усеченный треугольник», в котором не хватает первых двух строк, легко сделать полным (получить строчки при n=0 и n=1):

Общая формула бинома Ньютона:

.

Правая часть формулы называется разложением степени бинома.

— называется биномиальными коэффициентами, а все слагаемые — членами бинома.

Треугольник Паскаля — бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Назван в честь Блеза Паскаля.

Европейские ученые познакомились с формулой бинома Ньютона, по-видимому, через восточных математиков. Детальное изучение свойств биномиальных коэффициентов провел французский математик и философ Б. Паскаль в 1654 г.

В заключении рассмотрим пример, в котором использование бинома Ньютона позволяет доказать делимость выражения на заданное число.

Доказать, что значение выражения 5 n +28n-1, где n – натуральное число, делится на 16 без остатка.

Решение: представим первое слагаемое выражение как 5 n = (4+1) n и воспользуемся формулой бинома Ньютона:

Полученное произведение доказывает делимость исходного выражения на 16.

Бином Ньютона применяется при доказательстве Теоремы Ферма, в теории бесконечных рядов и выводе формулы Ньютона-Лейбница

Примеры и разборы решения заданий тренировочного модуля

Из данных многочленов выделите симметрические:

Решение: к данному заданию применим определение симметрических многочленов (Многочлен Р(х;у) называют симметрическим, если он сохраняет свой вид при одновременной замене х на у и у на х). Получим, что нам подходят 1 и 4 пункты.

(а+b) 5 = __a 5 +___a 4 b+___a 3 b 2 +___a 2 b 3 +___ab 4 +__b 5

Решение: для решения данного задания воспользуемся треугольником Паскаля

1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1

Нас интересует последняя строчка.

Применив ее, получим ответ:

(а+b) 5 = 1a 5 +5a 4 b+10a 3 b 2 +10a 2 b 3 +5ab 4 +1b 5

Источник

Полиномы

где c_i фиксированные коэффициенты, а x — переменная. Многочлены составляют один из важнейших классов элементарных функций.

Изучение полиномиальных уравнений и их решений составляло едва ли не главный объект «классической алгебры». С изучением многочленов связан целый ряд преобразований в математике: введение в рассмотрение нуля, отрицательных, а затем и комплексных чисел, а также появление теории групп как раздела математики и выделение классов специальных функций в анализе.

Техническая простота вычислений, связанных с многочленами, по сравнению с более сложными классами функций, а также тот факт, что множество многочленов плотно в пространстве непрерывных функций на компактных подмножествах евклидова пространства (смотри аппроксимационная теорема Вейерштрасса), способствовали развитию методов разложения в ряды и полиномиальной интерполяции в математическом анализе.

Многочлены также играют ключевую роль в алгебраической геометрии, объектом которой являются множества, определённые как решения систем многочленов. Особые свойства преобразования коэффициентов при умножении многочленов используются в алгебраической геометрии, алгебре, теории узлов и других разделах математики для кодирования, или выражения многочленами свойств различных объектов.

Содержание

Определение

Многочлен (или полином) от n переменных — есть конечная формальная сумма вида

,

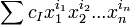
где I = (i₁,i₂. i_n) есть набор из целых неотрицательных чисел (называется мультииндекс), c_I — число (называемое «коэффициент многочлена»), зависящее только от мультииндекса I.

В частности, многочлен от одной переменной есть конечная формальная сумма вида

Коэффициенты многочлена обычно берутся из определённого коммутативного кольца R (чаще всего поля, например, поля вещественных или комплексных чисел). В этом случае, относительно операций сложения и умножения многочлены образуют кольцо (более того ассоциативно-коммутативную алгебру над кольцом R без делителей нуля) которое обозначается

Связанные определения

Делимость

Например, многочлен x 4 + 2, неприводимый в поле рациональных чисел, разлагается на два множителя в поле вещественных чисел и на четыре множителя в поле комплексных чисел.

Вообще, каждый многочлен от одного переменного x разлагается в поле вещественных чисел на множители первой и второй степени, в поле комплексных чисел — на множители первой степени (основная теорема алгебры).

Для двух и большего числа переменных этого уже нельзя утверждать. Над любым полем для любого n > 2 существуют многочлен от n переменных, неприводимые в любом расширении этого поля. Такие многочлены называются абсолютно неприводимыми.

Полиномиальные функции

.

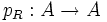
В случае если R есть поле вещественных или комплексных чисел (а также любое другое поле с бесконечным числом элементов) то функция полностью определяет многочлен p. Однако в общем случае это неверно, например: многочлены и из определяют тождественно равные функции .

Источник